华师大版七年级数学上册4.3《立体图形的表面展开图》专题训练(word版含答案)
文档属性
| 名称 | 华师大版七年级数学上册4.3《立体图形的表面展开图》专题训练(word版含答案) |
|
|
| 格式 | doc | ||
| 文件大小 | 260.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 华东师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-10-19 00:00:00 | ||
图片预览

文档简介
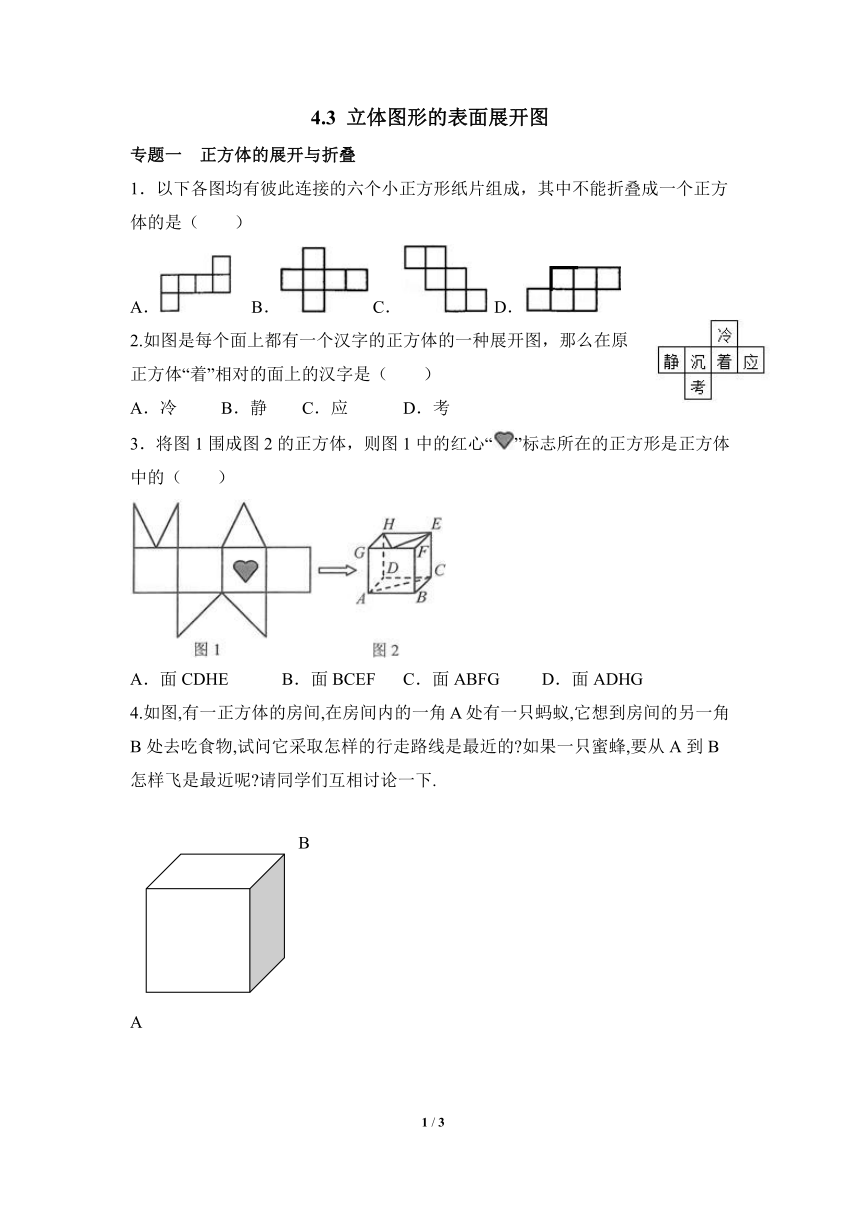
4.3 立体图形的表面展开图
专题一 正方体的展开与折叠
1.以下各图均有彼此连接的六个小正方形纸片组成,其中不能折叠成一个正方体的是( )
A. B. C. D.
2.如图是每个面上都有一个汉字的正方体的一种展开图,那么在原正方体“着”相对的面上的汉字是( )
A.冷 B.静 C.应 D.考
3.将图1围成图2的正方体,则图1中的红心“”标志所在的正方形是正方体中的( )
A.面CDHE B.面BCEF C.面ABFG D.面ADHG
4.如图,有一正方体的房间,在房间内的一角A处有一只蚂蚁,它想到房间的另一角B处去吃食物,试问它采取怎样的行走路线是最近的 如果一只蜜蜂,要从A到B怎样飞是最近呢 请同学们互相讨论一下.
B
A
专题二 三棱柱、圆柱与圆锥的展开与折叠
5.左图是一个三棱柱,下列图形中,能通过折叠围成该三棱柱的是( )
A.B.C.D.
6.如下图所示的平面图形中,不可能围成圆锥的是( )
A. B. C. D.
状元笔记:
【知识要点】
1.掌握正方体的展开与折叠,能根据所给平面图形判断是否能折叠成正方体.
2.根据简单立体图形的形状画出它的展开图,根据展开图判断立体图形的形状.
【温馨提示】
1.长方体有8个顶点,12条棱,6个面,且每个面都是长方形(正方形是特殊的长方形).
长方体是四棱柱,但四棱柱不一定是长方体,四棱柱的两个底面是四边形,不一定是长方形.
2.一个平面展开图,折成立体图形的方式有两种:一种是向里折,一种是向外折,一般易忽略其中一种,造成漏解.
3.棱柱的表面展开图是由两个相同的多边形和一些长方形连成的,沿棱柱表面不同的棱剪开,可能得到不同组合方式的平面展开图;圆柱的表面展开图是由两个相同的圆形和一个长方形连成的;圆锥的表面展开图是由一个圆形和一个扇形连成的.
【方法技巧】
确定正方体展开图的方法以口诀的方式总结出来:正方体经7刀剪,可得六面十四边;中间并排达四面,两旁各一随便站;三面并排在中间,单面任意双面偏;三层两面两层三,好似阶梯入云天;再问邻面何特点,“间二”“拐角”是关键; “隔1”、“Z端”是对面,识图巧排“七”“凹”“田”.
参考答案:
1.D 解析:选项A、B、C都可以折叠成一个正方体;选项D,有“田”字格,所以不能折叠成一个正方体.故选D.
考点:展开图折叠成几何体.
分析:由平面图形的折叠及正方体的展开图解题.能组成正方体的“一,四,一”“三,三”“二,二,二”“一,三,二”的基本形态要记牢.
2.B 解析:这是一个正方体的平面展开图,共有六个面,其中面“静”与面“着”相对,面“沉”与面“应”相对,“冷”与面“考”相对.
3.A 解析:由图1中的红心“”标志,可知它与等边三角形相邻,折叠成正方体是正方体中的面CDHE.
考点:展开图折叠成几何体.
分析:由平面图形的折叠及正方体的展开图解题,注意找准红心“”标志所在的相邻面.
4.解:如图(1)所示,线段AB是蚂蚁行走的最近路线;如图(2)所示,线段AB是蜜蜂飞的最近路线.
5.B 解析:A.折叠后有二个侧面重合,不能得到三棱柱; B.折叠后可得到三棱柱;C.折叠后有二个底面重合,不能得到三棱柱; D.多了一个底面,不能得到三棱柱.
6.D 解析:根据圆锥的侧面展开图是扇形,可以直接得出答案,D选项不符合要求.
1 / 3
专题一 正方体的展开与折叠
1.以下各图均有彼此连接的六个小正方形纸片组成,其中不能折叠成一个正方体的是( )
A. B. C. D.
2.如图是每个面上都有一个汉字的正方体的一种展开图,那么在原正方体“着”相对的面上的汉字是( )
A.冷 B.静 C.应 D.考
3.将图1围成图2的正方体,则图1中的红心“”标志所在的正方形是正方体中的( )
A.面CDHE B.面BCEF C.面ABFG D.面ADHG
4.如图,有一正方体的房间,在房间内的一角A处有一只蚂蚁,它想到房间的另一角B处去吃食物,试问它采取怎样的行走路线是最近的 如果一只蜜蜂,要从A到B怎样飞是最近呢 请同学们互相讨论一下.
B
A
专题二 三棱柱、圆柱与圆锥的展开与折叠
5.左图是一个三棱柱,下列图形中,能通过折叠围成该三棱柱的是( )
A.B.C.D.
6.如下图所示的平面图形中,不可能围成圆锥的是( )
A. B. C. D.
状元笔记:
【知识要点】
1.掌握正方体的展开与折叠,能根据所给平面图形判断是否能折叠成正方体.
2.根据简单立体图形的形状画出它的展开图,根据展开图判断立体图形的形状.
【温馨提示】
1.长方体有8个顶点,12条棱,6个面,且每个面都是长方形(正方形是特殊的长方形).
长方体是四棱柱,但四棱柱不一定是长方体,四棱柱的两个底面是四边形,不一定是长方形.
2.一个平面展开图,折成立体图形的方式有两种:一种是向里折,一种是向外折,一般易忽略其中一种,造成漏解.
3.棱柱的表面展开图是由两个相同的多边形和一些长方形连成的,沿棱柱表面不同的棱剪开,可能得到不同组合方式的平面展开图;圆柱的表面展开图是由两个相同的圆形和一个长方形连成的;圆锥的表面展开图是由一个圆形和一个扇形连成的.
【方法技巧】
确定正方体展开图的方法以口诀的方式总结出来:正方体经7刀剪,可得六面十四边;中间并排达四面,两旁各一随便站;三面并排在中间,单面任意双面偏;三层两面两层三,好似阶梯入云天;再问邻面何特点,“间二”“拐角”是关键; “隔1”、“Z端”是对面,识图巧排“七”“凹”“田”.
参考答案:
1.D 解析:选项A、B、C都可以折叠成一个正方体;选项D,有“田”字格,所以不能折叠成一个正方体.故选D.
考点:展开图折叠成几何体.
分析:由平面图形的折叠及正方体的展开图解题.能组成正方体的“一,四,一”“三,三”“二,二,二”“一,三,二”的基本形态要记牢.
2.B 解析:这是一个正方体的平面展开图,共有六个面,其中面“静”与面“着”相对,面“沉”与面“应”相对,“冷”与面“考”相对.
3.A 解析:由图1中的红心“”标志,可知它与等边三角形相邻,折叠成正方体是正方体中的面CDHE.
考点:展开图折叠成几何体.
分析:由平面图形的折叠及正方体的展开图解题,注意找准红心“”标志所在的相邻面.
4.解:如图(1)所示,线段AB是蚂蚁行走的最近路线;如图(2)所示,线段AB是蜜蜂飞的最近路线.
5.B 解析:A.折叠后有二个侧面重合,不能得到三棱柱; B.折叠后可得到三棱柱;C.折叠后有二个底面重合,不能得到三棱柱; D.多了一个底面,不能得到三棱柱.
6.D 解析:根据圆锥的侧面展开图是扇形,可以直接得出答案,D选项不符合要求.
1 / 3
同课章节目录
- 第1章 走进数学世界
- 数学伴我们成长
- 人类离不开数学
- 人人都能学会数学
- 第2章 有理数
- 2.1 有理数
- 2.2 数轴
- 2.3 相反数
- 2.4 绝对值
- 2.5 有理数的大小比较
- 2.6 有理数的加法
- 2.7 有理数的减法
- 2.8 有理数加减混合运算
- 2.9 有理数的乘法
- 2.10 有理数的除法
- 2.11 有理数的乘方
- 2.12 科学记数法
- 2.13 有理数的混合运算
- 2.14 近似数
- 2.15 用计算器进行计算
- 第3章 整式的加减
- 3.1 列代数式
- 3.2 代数式的值
- 3.3 整式
- 3.4 整式的加减
- 第4章 图形的初步认识
- 4.1 生活中的立体图形
- 4.2 立体图形的视图
- 4.3 立体图形的表面展开图
- 4.4 平面图形
- 4.5 最基本的图形——点和线
- 4.6 角
- 第5章 相交线与平行线
- 5.1 相交线
- 5.2 平行线
