人教版2021-2022学年七年级册数学上册3.1实际问题与一元一次方程基础专项训练(word版含解析)
文档属性
| 名称 | 人教版2021-2022学年七年级册数学上册3.1实际问题与一元一次方程基础专项训练(word版含解析) |

|
|
| 格式 | docx | ||
| 文件大小 | 109.2KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-10-19 13:00:07 | ||
图片预览




文档简介
人教版七年级第一学期数学基础专项训练
01实际问题与一元一次方程
一.选择题
1.把1400元的奖金按两种等次奖给22名学生,其中一等奖每人200元,二等奖每人50元,设获一等奖的学生有x人,则下列选项所列方程错误的是( )
A.(200-50)x+50×22=1400 B.50x+200(22-x)=1400
C.200x+50(22-x)=1400 D.
2.某车间有28名工人生产螺钉和螺母,每人每小时平均能生产螺钉12个或螺母18个,1个螺钉需要配2个螺母,若安排m名工人生产螺钉时每小时生产的螺栓和螺母刚好配套,那么可列方程为( )
A.12×m=18×(28-m)×2 B.12×(28-m)=18×m×2
C.12×m×2=18×(28-m) D.12×(28-m)×2=18×m
3.书架上,第一层的数量是第二层书的数量x的2倍,从第一层抽8本到第二层,这时第一层剩下的数量恰比第二层的一半多3本.依上述情形,所列关系式成立的是( )
A.2x=x+3 B.2x=(x+8)+3
C.2x-8=x+3 D.2x-8=(x+8)+3
4.一套仪器由一个A部件和三个B部件构成,用1m3钢材可做40个A部件或240个B部件,现要用6m3钢材制作这种仪器,设应用xm3钢材做B部件,其他钢材做A部件,恰好配套,则可列方程为( )
A.3×40x=240(6-x) B.3×240x=40(6-x)
C.40x=3×240(6-x) D.240x=3×40(6-x)
5.商店将进价2400元的彩电标价3600元出售,为了吸引顾客进行打折出售,售后核算仍可获利20%,则折扣为( )
A.九折 B.八五折 C.八折 D.七五折
6.某制衣店现购买蓝色、黑色两种布料共138m,共花费540元.其中蓝色布料每米3元,黑色布料每米5元,两种布料各买多少米?设买蓝色布料x米,则依题意可列方程( )
A.3x+5(138-x)=540 B.5x+3(138-x)=540
C.3x+5(138+x)=540 D.5x+3(138+x)=540
7.甲、乙两运动员在长为400m的环形跑道上进行匀速跑训练,两人同时从起点出发,同向而行,若甲跑步的速度为5m/s,乙跑步的速度为4m/s,则起跑后500s内,两人相遇的次数为( )
A.0 B.1 C.2 D.3
8.某超市以同样的价格卖出甲、乙两件商品,其中甲商品获利20%,乙商品亏损20%,若甲商品的成本价是80元,则乙商品的成本价是( )
A.90元 B.72元 C.120元 D.80元
9.中国古代数学著作《算法统宗》中有这样一段记载:“三百七十八里关,初日健步不为难,次日脚痛减一半,六朝才得到其关.”其大意是,有人要去某关口,路程为378里,第一天健步行走,从第二天起,由于脚痛.每天走的路程都为前一天的一半,一共走了六天才到达目的地,则此人第五天走的路程为( )
A.24里 B.12里 C.6里 D.3里
10.如图,小明将一个正方形纸剪出一个宽为4cm的长条后,再从剩下的长方形纸片上剪去一个宽为5cm的长条,如果两次剪下的长条面积正好相等,那么每一个长条面积为( )
A.16cm2 B.20cm2 C.80cm2 D.160cm2
二.填空题
11.某小组计划做一批中国结,如果每人做6个,那么比计划多做了9个;如果每人做4个,那么比计划少7个.设计划做x个中国结,可列方程 .
12.元旦期间,某超市推出如下优惠方案:(1)一次性购物价值超过100元但不超过300元,原价基础上一律9折.(2)一次性购物超过300元,原价基础上一律8折.王老师购物后付款252元,则他所购物品的原价是 元.
13.某学校需要购买一批电脑,有两种方案如下:方案1:到商家直接购买,每台需要7000元;方案2:学校买零部件组装,每台需要6000元,另外需要支付安装费等其它费用合计3000元.学校添置 台电脑时,两种方案的费用相同.
14.某商场对某种商品作调价,按原价8折出售,此时商品的利润率是10%,若商品的进价为1200元,则商品的原价是 元.
三.解答题
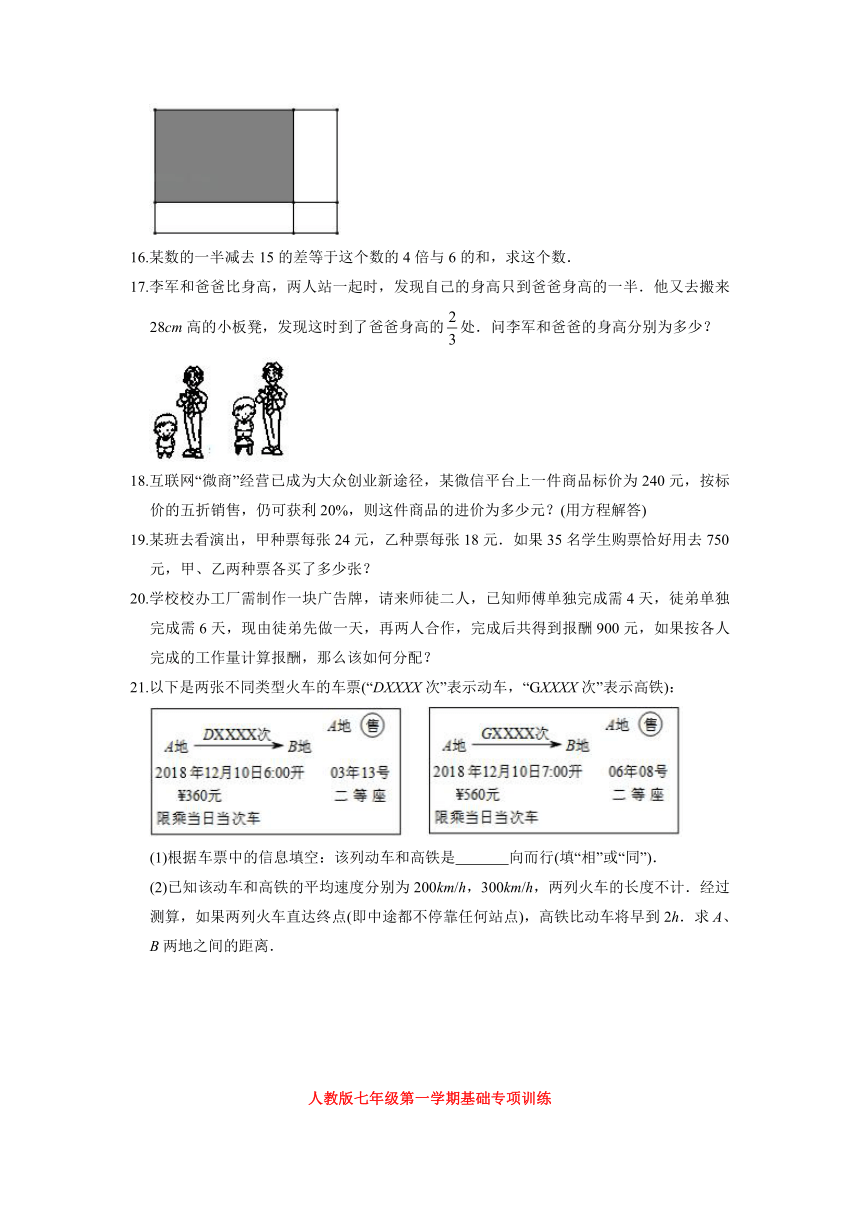
15.如图所示,长方形纸片的长为15厘米,在这张纸片的长和宽上各剪去一个宽为3厘米的纸条,剩余部分(阴影部分)的面积是60平方厘米,求原长方形纸片的宽.
16.某数的一半减去15的差等于这个数的4倍与6的和,求这个数.
17.李军和爸爸比身高,两人站一起时,发现自己的身高只到爸爸身高的一半.他又去搬来28cm高的小板凳,发现这时到了爸爸身高的处.问李军和爸爸的身高分别为多少?
18.互联网“微商”经营已成为大众创业新途径,某微信平台上一件商品标价为240元,按标价的五折销售,仍可获利20%,则这件商品的进价为多少元?(用方程解答)
19.某班去看演出,甲种票每张24元,乙种票每张18元.如果35名学生购票恰好用去750元,甲、乙两种票各买了多少张?
20.学校校办工厂需制作一块广告牌,请来师徒二人,已知师傅单独完成需4天,徒弟单独完成需6天,现由徒弟先做一天,再两人合作,完成后共得到报酬900元,如果按各人完成的工作量计算报酬,那么该如何分配?
21.以下是两张不同类型火车的车票(“DXXXX次”表示动车,“GXXXX次”表示高铁):
(1)根据车票中的信息填空:该列动车和高铁是 向而行(填“相”或“同”).
(2)已知该动车和高铁的平均速度分别为200km/h,300km/h,两列火车的长度不计.经过测算,如果两列火车直达终点(即中途都不停靠任何站点),高铁比动车将早到2h.求A、B两地之间的距离.
人教版七年级第一学期基础专项训练
01实际问题与一元一次方程参考答案
一.选择题
1.把1400元的奖金按两种等次奖给22名学生,其中一等奖每人200元,二等奖每人50元,设获一等奖的学生有x人,则下列选项所列方程错误的是( )
A.(200-50)x+50×22=1400 B.50x+200(22-x)=1400
C.200x+50(22-x)=1400 D.
解:设获一等奖的学生有x人,则获二等奖的学生有(22-x)人,
依题意,得:200x+50(22-x)=1400,(200-50)x+50×22=1400,.
故选:B.
2.某车间有28名工人生产螺钉和螺母,每人每小时平均能生产螺钉12个或螺母18个,1个螺钉需要配2个螺母,若安排m名工人生产螺钉时每小时生产的螺栓和螺母刚好配套,那么可列方程为( )
A.12×m=18×(28-m)×2 B.12×(28-m)=18×m×2
C.12×m×2=18×(28-m) D.12×(28-m)×2=18×m
解:设安排m名工人生产螺钉,则(28-m)人生产螺母,由题意得
12×m×2=18×(28-m),
故选:C.
3.书架上,第一层的数量是第二层书的数量x的2倍,从第一层抽8本到第二层,这时第一层剩下的数量恰比第二层的一半多3本.依上述情形,所列关系式成立的是( )
A.2x=x+3 B.2x=(x+8)+3
C.2x-8=x+3 D.2x-8=(x+8)+3
解:由题意知,第一层书的数量为2x本,则可得到方程2x-8=(x+8)+3.故选:D.
4.一套仪器由一个A部件和三个B部件构成,用1m3钢材可做40个A部件或240个B部件,现要用6m3钢材制作这种仪器,设应用xm3钢材做B部件,其他钢材做A部件,恰好配套,则可列方程为( )
A.3×40x=240(6-x) B.3×240x=40(6-x)
C.40x=3×240(6-x) D.240x=3×40(6-x)
解:设应用xm3钢材做B部件,则应用(6-x)m3钢材做A部件,
由题意得,240x=3×40(6-x)
故选:D.
5.商店将进价2400元的彩电标价3600元出售,为了吸引顾客进行打折出售,售后核算仍可获利20%,则折扣为( )
A.九折 B.八五折 C.八折 D.七五折
解:设折扣为x折,
根据题意得:3600×-2400=2400×20%,
解得:x=8,
则折扣为八折,
故选:C.
6.某制衣店现购买蓝色、黑色两种布料共138m,共花费540元.其中蓝色布料每米3元,黑色布料每米5元,两种布料各买多少米?设买蓝色布料x米,则依题意可列方程( )
A.3x+5(138-x)=540 B.5x+3(138-x)=540
C.3x+5(138+x)=540 D.5x+3(138+x)=540
解:设买蓝色布料x米,则买黑色布料(138-x)米,根据题意可得:
3x+5(138-x)=540,
故选:A.
7.甲、乙两运动员在长为400m的环形跑道上进行匀速跑训练,两人同时从起点出发,同向而行,若甲跑步的速度为5m/s,乙跑步的速度为4m/s,则起跑后500s内,两人相遇的次数为( )
A.0 B.1 C.2 D.3
解:设甲、乙同向而跑,经过xs时间甲乙能相遇,
依题意有:(5-4)x=400,
解得x=400.
由于1<=<2.
所以两人相遇的次数为1.
故选:B.
8.某超市以同样的价格卖出甲、乙两件商品,其中甲商品获利20%,乙商品亏损20%,若甲商品的成本价是80元,则乙商品的成本价是( )
A.90元 B.72元 C.120元 D.80元
解:设甲商品以x元出售,
由题意可知:×100%=20%,
解得:x=96,
设乙商品的成本价为y元,
∴96-y=-20%×y,
解得:y=120,
故选:C.
9.中国古代数学著作《算法统宗》中有这样一段记载:“三百七十八里关,初日健步不为难,次日脚痛减一半,六朝才得到其关.”其大意是,有人要去某关口,路程为378里,第一天健步行走,从第二天起,由于脚痛.每天走的路程都为前一天的一半,一共走了六天才到达目的地,则此人第五天走的路程为( )
A.24里 B.12里 C.6里 D.3里
解:设第一天走了x里,
依题意得:x+x+x+x+x+x=378,
解得x=192.
则()4x=()4×192=12(里).
故选:B.
10.如图,小明将一个正方形纸剪出一个宽为4cm的长条后,再从剩下的长方形纸片上剪去一个宽为5cm的长条,如果两次剪下的长条面积正好相等,那么每一个长条面积为( )
A.16cm2 B.20cm2 C.80cm2 D.160cm2
解:设原来正方形纸的边长是xcm,则第一次剪下的长条的长是xcm,宽是4cm,第二次剪下的长条的长是x-4cm,宽是5cm,
则4x=5(x-4),
去括号,可得:4x=5x-20,
移项,可得:5x-4x=20,
解得x=20
4x=4×20=80(cm2)
所以每一个长条面积为80cm2.
故选:C.
二.填空题
11.某小组计划做一批中国结,如果每人做6个,那么比计划多做了9个;如果每人做4个,那么比计划少7个.设计划做x个中国结,可列方程 .
解:设计划做x个“中国结”,根据题意得.
故答案为.
12.元旦期间,某超市推出如下优惠方案:(1)一次性购物价值超过100元但不超过300元,原价基础上一律9折.(2)一次性购物超过300元,原价基础上一律8折.王老师购物后付款252元,则他所购物品的原价是 元.
解:设他所购物品的原价是x元,分两种情况:
①如果是第(1)种优惠,可得0.9x=252,解得x=280(符合超过100不高于300);
②如果是第(2)种优惠,可得0.8x=252,解得x=315(符合超过300元).
他所购物品的原价是:280或315元.
故答案为:280或315.
13.某学校需要购买一批电脑,有两种方案如下:方案1:到商家直接购买,每台需要7000元;方案2:学校买零部件组装,每台需要6000元,另外需要支付安装费等其它费用合计3000元.学校添置 台电脑时,两种方案的费用相同.
解:设学校添置x台电脑,
由题意,得7000x=6000x+3000,
解得x=3,
答:当学校添置3台电脑时,两种方案的费用相同;
故答案是:3.
14.某商场对某种商品作调价,按原价8折出售,此时商品的利润率是10%,若商品的进价为1200元,则商品的原价是 元.
解:设该商品的原价为每件x元,由题意得,
0.8x-1200=1200×10%,
解得:x=1650.
答:该商品的原价为每件1650元.
故答案为:1650.
三.解答题
15.如图所示,长方形纸片的长为15厘米,在这张纸片的长和宽上各剪去一个宽为3厘米的纸条,剩余部分(阴影部分)的面积是60平方厘米,求原长方形纸片的宽.
解:设原长方形纸片的宽为x厘米,
根据题意可得:(15-3)(x-3)=60,
解得:x=8,
答:原长方形纸片的宽为8厘米.
16.某数的一半减去15的差等于这个数的4倍与6的和,求这个数.
解:设这个数为x,
依题意,得:x-15=4x+6,
解得:x=-6.
答:这个数是-6.
17.李军和爸爸比身高,两人站一起时,发现自己的身高只到爸爸身高的一半.他又去搬来28cm高的小板凳,发现这时到了爸爸身高的处.问李军和爸爸的身高分别为多少?
解:设李军的身高为xcm,则爸爸的身高为2xcm,
根据题意,得x+28= 2x,
解得:x=84,
则2x=168.
答:李军的身高是84cm,爸爸的身高是168cm.
18.互联网“微商”经营已成为大众创业新途径,某微信平台上一件商品标价为240元,按标价的五折销售,仍可获利20%,则这件商品的进价为多少元?(用方程解答)
解:设这件商品的进价为x元,
∴240×0.5-x=0.2x,
解得:x=100,
答:这件商品的进价为100元.
19.某班去看演出,甲种票每张24元,乙种票每张18元.如果35名学生购票恰好用去750元,甲、乙两种票各买了多少张?
解:设甲种票买了x张,则乙种票买了(35-x)张.
由题意,得24x+18(35-x)=750,
解得x=20,
所以35-x=15.
答:甲种票买了20张,乙种票买了15张.
20.学校校办工厂需制作一块广告牌,请来师徒二人,已知师傅单独完成需4天,徒弟单独完成需6天,现由徒弟先做一天,再两人合作,完成后共得到报酬900元,如果按各人完成的工作量计算报酬,那么该如何分配?
解:设两人一起做了x天,
依题意,得:(x+1)+x=1,
解得:x=2,
师傅应得报酬为×2×900=450(元);
徒弟应得报酬为×(1+2)×900=450(元).
答:师傅应得报酬为450元,徒弟应得报酬为450元.
21.以下是两张不同类型火车的车票(“DXXXX次”表示动车,“GXXXX次”表示高铁):
(1)根据车票中的信息填空:该列动车和高铁是 向而行(填“相”或“同”).
(2)已知该动车和高铁的平均速度分别为200km/h,300km/h,两列火车的长度不计.经过测算,如果两列火车直达终点(即中途都不停靠任何站点),高铁比动车将早到2h.求A、B两地之间的距离.
解(1)根据车票中的信息填空:该列动车和高铁是同向而行.
(2)设A、B两地之间的距离为xkm,
根据题意得:,
解得:x=1800.
答:A、B两地之间的距离是1800km.
故答案为:同.
01实际问题与一元一次方程
一.选择题
1.把1400元的奖金按两种等次奖给22名学生,其中一等奖每人200元,二等奖每人50元,设获一等奖的学生有x人,则下列选项所列方程错误的是( )
A.(200-50)x+50×22=1400 B.50x+200(22-x)=1400
C.200x+50(22-x)=1400 D.
2.某车间有28名工人生产螺钉和螺母,每人每小时平均能生产螺钉12个或螺母18个,1个螺钉需要配2个螺母,若安排m名工人生产螺钉时每小时生产的螺栓和螺母刚好配套,那么可列方程为( )
A.12×m=18×(28-m)×2 B.12×(28-m)=18×m×2
C.12×m×2=18×(28-m) D.12×(28-m)×2=18×m
3.书架上,第一层的数量是第二层书的数量x的2倍,从第一层抽8本到第二层,这时第一层剩下的数量恰比第二层的一半多3本.依上述情形,所列关系式成立的是( )
A.2x=x+3 B.2x=(x+8)+3
C.2x-8=x+3 D.2x-8=(x+8)+3
4.一套仪器由一个A部件和三个B部件构成,用1m3钢材可做40个A部件或240个B部件,现要用6m3钢材制作这种仪器,设应用xm3钢材做B部件,其他钢材做A部件,恰好配套,则可列方程为( )
A.3×40x=240(6-x) B.3×240x=40(6-x)
C.40x=3×240(6-x) D.240x=3×40(6-x)
5.商店将进价2400元的彩电标价3600元出售,为了吸引顾客进行打折出售,售后核算仍可获利20%,则折扣为( )
A.九折 B.八五折 C.八折 D.七五折
6.某制衣店现购买蓝色、黑色两种布料共138m,共花费540元.其中蓝色布料每米3元,黑色布料每米5元,两种布料各买多少米?设买蓝色布料x米,则依题意可列方程( )
A.3x+5(138-x)=540 B.5x+3(138-x)=540
C.3x+5(138+x)=540 D.5x+3(138+x)=540
7.甲、乙两运动员在长为400m的环形跑道上进行匀速跑训练,两人同时从起点出发,同向而行,若甲跑步的速度为5m/s,乙跑步的速度为4m/s,则起跑后500s内,两人相遇的次数为( )
A.0 B.1 C.2 D.3
8.某超市以同样的价格卖出甲、乙两件商品,其中甲商品获利20%,乙商品亏损20%,若甲商品的成本价是80元,则乙商品的成本价是( )
A.90元 B.72元 C.120元 D.80元
9.中国古代数学著作《算法统宗》中有这样一段记载:“三百七十八里关,初日健步不为难,次日脚痛减一半,六朝才得到其关.”其大意是,有人要去某关口,路程为378里,第一天健步行走,从第二天起,由于脚痛.每天走的路程都为前一天的一半,一共走了六天才到达目的地,则此人第五天走的路程为( )
A.24里 B.12里 C.6里 D.3里
10.如图,小明将一个正方形纸剪出一个宽为4cm的长条后,再从剩下的长方形纸片上剪去一个宽为5cm的长条,如果两次剪下的长条面积正好相等,那么每一个长条面积为( )
A.16cm2 B.20cm2 C.80cm2 D.160cm2
二.填空题
11.某小组计划做一批中国结,如果每人做6个,那么比计划多做了9个;如果每人做4个,那么比计划少7个.设计划做x个中国结,可列方程 .
12.元旦期间,某超市推出如下优惠方案:(1)一次性购物价值超过100元但不超过300元,原价基础上一律9折.(2)一次性购物超过300元,原价基础上一律8折.王老师购物后付款252元,则他所购物品的原价是 元.
13.某学校需要购买一批电脑,有两种方案如下:方案1:到商家直接购买,每台需要7000元;方案2:学校买零部件组装,每台需要6000元,另外需要支付安装费等其它费用合计3000元.学校添置 台电脑时,两种方案的费用相同.
14.某商场对某种商品作调价,按原价8折出售,此时商品的利润率是10%,若商品的进价为1200元,则商品的原价是 元.
三.解答题
15.如图所示,长方形纸片的长为15厘米,在这张纸片的长和宽上各剪去一个宽为3厘米的纸条,剩余部分(阴影部分)的面积是60平方厘米,求原长方形纸片的宽.
16.某数的一半减去15的差等于这个数的4倍与6的和,求这个数.
17.李军和爸爸比身高,两人站一起时,发现自己的身高只到爸爸身高的一半.他又去搬来28cm高的小板凳,发现这时到了爸爸身高的处.问李军和爸爸的身高分别为多少?
18.互联网“微商”经营已成为大众创业新途径,某微信平台上一件商品标价为240元,按标价的五折销售,仍可获利20%,则这件商品的进价为多少元?(用方程解答)
19.某班去看演出,甲种票每张24元,乙种票每张18元.如果35名学生购票恰好用去750元,甲、乙两种票各买了多少张?
20.学校校办工厂需制作一块广告牌,请来师徒二人,已知师傅单独完成需4天,徒弟单独完成需6天,现由徒弟先做一天,再两人合作,完成后共得到报酬900元,如果按各人完成的工作量计算报酬,那么该如何分配?
21.以下是两张不同类型火车的车票(“DXXXX次”表示动车,“GXXXX次”表示高铁):
(1)根据车票中的信息填空:该列动车和高铁是 向而行(填“相”或“同”).
(2)已知该动车和高铁的平均速度分别为200km/h,300km/h,两列火车的长度不计.经过测算,如果两列火车直达终点(即中途都不停靠任何站点),高铁比动车将早到2h.求A、B两地之间的距离.
人教版七年级第一学期基础专项训练
01实际问题与一元一次方程参考答案
一.选择题
1.把1400元的奖金按两种等次奖给22名学生,其中一等奖每人200元,二等奖每人50元,设获一等奖的学生有x人,则下列选项所列方程错误的是( )
A.(200-50)x+50×22=1400 B.50x+200(22-x)=1400
C.200x+50(22-x)=1400 D.
解:设获一等奖的学生有x人,则获二等奖的学生有(22-x)人,
依题意,得:200x+50(22-x)=1400,(200-50)x+50×22=1400,.
故选:B.
2.某车间有28名工人生产螺钉和螺母,每人每小时平均能生产螺钉12个或螺母18个,1个螺钉需要配2个螺母,若安排m名工人生产螺钉时每小时生产的螺栓和螺母刚好配套,那么可列方程为( )
A.12×m=18×(28-m)×2 B.12×(28-m)=18×m×2
C.12×m×2=18×(28-m) D.12×(28-m)×2=18×m
解:设安排m名工人生产螺钉,则(28-m)人生产螺母,由题意得
12×m×2=18×(28-m),
故选:C.
3.书架上,第一层的数量是第二层书的数量x的2倍,从第一层抽8本到第二层,这时第一层剩下的数量恰比第二层的一半多3本.依上述情形,所列关系式成立的是( )
A.2x=x+3 B.2x=(x+8)+3
C.2x-8=x+3 D.2x-8=(x+8)+3
解:由题意知,第一层书的数量为2x本,则可得到方程2x-8=(x+8)+3.故选:D.
4.一套仪器由一个A部件和三个B部件构成,用1m3钢材可做40个A部件或240个B部件,现要用6m3钢材制作这种仪器,设应用xm3钢材做B部件,其他钢材做A部件,恰好配套,则可列方程为( )
A.3×40x=240(6-x) B.3×240x=40(6-x)
C.40x=3×240(6-x) D.240x=3×40(6-x)
解:设应用xm3钢材做B部件,则应用(6-x)m3钢材做A部件,
由题意得,240x=3×40(6-x)
故选:D.
5.商店将进价2400元的彩电标价3600元出售,为了吸引顾客进行打折出售,售后核算仍可获利20%,则折扣为( )
A.九折 B.八五折 C.八折 D.七五折
解:设折扣为x折,
根据题意得:3600×-2400=2400×20%,
解得:x=8,
则折扣为八折,
故选:C.
6.某制衣店现购买蓝色、黑色两种布料共138m,共花费540元.其中蓝色布料每米3元,黑色布料每米5元,两种布料各买多少米?设买蓝色布料x米,则依题意可列方程( )
A.3x+5(138-x)=540 B.5x+3(138-x)=540
C.3x+5(138+x)=540 D.5x+3(138+x)=540
解:设买蓝色布料x米,则买黑色布料(138-x)米,根据题意可得:
3x+5(138-x)=540,
故选:A.
7.甲、乙两运动员在长为400m的环形跑道上进行匀速跑训练,两人同时从起点出发,同向而行,若甲跑步的速度为5m/s,乙跑步的速度为4m/s,则起跑后500s内,两人相遇的次数为( )
A.0 B.1 C.2 D.3
解:设甲、乙同向而跑,经过xs时间甲乙能相遇,
依题意有:(5-4)x=400,
解得x=400.
由于1<=<2.
所以两人相遇的次数为1.
故选:B.
8.某超市以同样的价格卖出甲、乙两件商品,其中甲商品获利20%,乙商品亏损20%,若甲商品的成本价是80元,则乙商品的成本价是( )
A.90元 B.72元 C.120元 D.80元
解:设甲商品以x元出售,
由题意可知:×100%=20%,
解得:x=96,
设乙商品的成本价为y元,
∴96-y=-20%×y,
解得:y=120,
故选:C.
9.中国古代数学著作《算法统宗》中有这样一段记载:“三百七十八里关,初日健步不为难,次日脚痛减一半,六朝才得到其关.”其大意是,有人要去某关口,路程为378里,第一天健步行走,从第二天起,由于脚痛.每天走的路程都为前一天的一半,一共走了六天才到达目的地,则此人第五天走的路程为( )
A.24里 B.12里 C.6里 D.3里
解:设第一天走了x里,
依题意得:x+x+x+x+x+x=378,
解得x=192.
则()4x=()4×192=12(里).
故选:B.
10.如图,小明将一个正方形纸剪出一个宽为4cm的长条后,再从剩下的长方形纸片上剪去一个宽为5cm的长条,如果两次剪下的长条面积正好相等,那么每一个长条面积为( )
A.16cm2 B.20cm2 C.80cm2 D.160cm2
解:设原来正方形纸的边长是xcm,则第一次剪下的长条的长是xcm,宽是4cm,第二次剪下的长条的长是x-4cm,宽是5cm,
则4x=5(x-4),
去括号,可得:4x=5x-20,
移项,可得:5x-4x=20,
解得x=20
4x=4×20=80(cm2)
所以每一个长条面积为80cm2.
故选:C.
二.填空题
11.某小组计划做一批中国结,如果每人做6个,那么比计划多做了9个;如果每人做4个,那么比计划少7个.设计划做x个中国结,可列方程 .
解:设计划做x个“中国结”,根据题意得.
故答案为.
12.元旦期间,某超市推出如下优惠方案:(1)一次性购物价值超过100元但不超过300元,原价基础上一律9折.(2)一次性购物超过300元,原价基础上一律8折.王老师购物后付款252元,则他所购物品的原价是 元.
解:设他所购物品的原价是x元,分两种情况:
①如果是第(1)种优惠,可得0.9x=252,解得x=280(符合超过100不高于300);
②如果是第(2)种优惠,可得0.8x=252,解得x=315(符合超过300元).
他所购物品的原价是:280或315元.
故答案为:280或315.
13.某学校需要购买一批电脑,有两种方案如下:方案1:到商家直接购买,每台需要7000元;方案2:学校买零部件组装,每台需要6000元,另外需要支付安装费等其它费用合计3000元.学校添置 台电脑时,两种方案的费用相同.
解:设学校添置x台电脑,
由题意,得7000x=6000x+3000,
解得x=3,
答:当学校添置3台电脑时,两种方案的费用相同;
故答案是:3.
14.某商场对某种商品作调价,按原价8折出售,此时商品的利润率是10%,若商品的进价为1200元,则商品的原价是 元.
解:设该商品的原价为每件x元,由题意得,
0.8x-1200=1200×10%,
解得:x=1650.
答:该商品的原价为每件1650元.
故答案为:1650.
三.解答题
15.如图所示,长方形纸片的长为15厘米,在这张纸片的长和宽上各剪去一个宽为3厘米的纸条,剩余部分(阴影部分)的面积是60平方厘米,求原长方形纸片的宽.
解:设原长方形纸片的宽为x厘米,
根据题意可得:(15-3)(x-3)=60,
解得:x=8,
答:原长方形纸片的宽为8厘米.
16.某数的一半减去15的差等于这个数的4倍与6的和,求这个数.
解:设这个数为x,
依题意,得:x-15=4x+6,
解得:x=-6.
答:这个数是-6.
17.李军和爸爸比身高,两人站一起时,发现自己的身高只到爸爸身高的一半.他又去搬来28cm高的小板凳,发现这时到了爸爸身高的处.问李军和爸爸的身高分别为多少?
解:设李军的身高为xcm,则爸爸的身高为2xcm,
根据题意,得x+28= 2x,
解得:x=84,
则2x=168.
答:李军的身高是84cm,爸爸的身高是168cm.
18.互联网“微商”经营已成为大众创业新途径,某微信平台上一件商品标价为240元,按标价的五折销售,仍可获利20%,则这件商品的进价为多少元?(用方程解答)
解:设这件商品的进价为x元,
∴240×0.5-x=0.2x,
解得:x=100,
答:这件商品的进价为100元.
19.某班去看演出,甲种票每张24元,乙种票每张18元.如果35名学生购票恰好用去750元,甲、乙两种票各买了多少张?
解:设甲种票买了x张,则乙种票买了(35-x)张.
由题意,得24x+18(35-x)=750,
解得x=20,
所以35-x=15.
答:甲种票买了20张,乙种票买了15张.
20.学校校办工厂需制作一块广告牌,请来师徒二人,已知师傅单独完成需4天,徒弟单独完成需6天,现由徒弟先做一天,再两人合作,完成后共得到报酬900元,如果按各人完成的工作量计算报酬,那么该如何分配?
解:设两人一起做了x天,
依题意,得:(x+1)+x=1,
解得:x=2,
师傅应得报酬为×2×900=450(元);
徒弟应得报酬为×(1+2)×900=450(元).
答:师傅应得报酬为450元,徒弟应得报酬为450元.
21.以下是两张不同类型火车的车票(“DXXXX次”表示动车,“GXXXX次”表示高铁):
(1)根据车票中的信息填空:该列动车和高铁是 向而行(填“相”或“同”).
(2)已知该动车和高铁的平均速度分别为200km/h,300km/h,两列火车的长度不计.经过测算,如果两列火车直达终点(即中途都不停靠任何站点),高铁比动车将早到2h.求A、B两地之间的距离.
解(1)根据车票中的信息填空:该列动车和高铁是同向而行.
(2)设A、B两地之间的距离为xkm,
根据题意得:,
解得:x=1800.
答:A、B两地之间的距离是1800km.
故答案为:同.
