人教版2021-2022学年八年级数学上册11.3.2 多边形的内角和知识点整理与同步练习(word版含答案)
文档属性
| 名称 | 人教版2021-2022学年八年级数学上册11.3.2 多边形的内角和知识点整理与同步练习(word版含答案) |  | |
| 格式 | docx | ||
| 文件大小 | 761.9KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-10-19 13:19:23 | ||
图片预览

文档简介
第11章 三角形
多边形的内角和
多边形的内角和公式:n边形的内角和等于(n-2)×180°。
多边形的内角和推理方法
方法1:如图1所示,从n边形的一个顶点引出(n-3)条对角线,这(n-3)条对角线把n边形分成(n-2)个三角形,每个三角形的内角和是180°,所以n边形的内角和为(n-2)×180°。
方法2:如图2所示,在n边形内任取一点P,连接PA1,PA2……PAn,把n边形分成n个三角形,这n个三角形的内角和为n ×180°,再减去一个周角,即得n边形的内角和为n×180° -360°=(n-2)×180°。
方法3:如图3所示,如图所示,在n边形的 一边上任取一点P与各顶点相连,得(n-1)个三角形,n边形内角和等于这(n-1)个三角形的内角和减去在点P 处的一个平角,即得n边形的内角和为(n-1)×180° -180° =(n-2)×180°。
多边形的外角和
性质:多边形的外角和等于360°。
多边形的边数与内角和、外角和的关系
1、n边形的内角和等于(n-2)·180°(n≥3,n是正整数),可见多边形内角和与边数n有关,每增加1条边,内角和增加180°.
2、多边形的外角和等于360°,与边数的多少无关.
3、正n边形:正n边形的内角的度数为,外角的度数为.
一.选择题(共10小题)
1.下列多边形中,内角和与外角和相等的是
A. B.
C. D.
2.一个多边形每一个外角都等于,则这个多边形的边数为
A.12 B.14 C.16 D.18
3.一个正多边形的一个内角是其外角的3倍,则正多边形的边数为
A.8 B.9 C.10 D.12
4.如图,小明从点出发,沿直线前进8米后向左转,再沿直线前进8米,又向左转,,照这样走下去,他第一次回到出发点时,走过的总路程为
A.48米 B.80米 C.96米 D.无限长
5.如果一个多边形的每一个外角都是,那么这个多边形的边数是
A.12 B.13 C.14 D.15
6.已知正多边形的一个内角是,则这个正多边形的边数是
A.九边形 B.八边形 C.七边形 D.六边形
7.如图,五边形的内角都相等,且,,则
A. B. C. D.
8.如图,将四边形去掉一个的角得到一个五边形,则与的和为
A. B. C. D.
9.如图,的度数为
A. B. C. D.
10.如图,图1是一个四边形纸条,其中,,分别为边,上的两个点,将纸条沿折叠得到图2,再将图2沿折叠得到图3,若在图3中,,则的度数为
A. B. C. D.
二.填空题(共4小题)
11.已知一个正多边形的一个外角为,则它的内角和为 .
12.如图,,,是五边形的3个外角,若,则 .
13.如图,在五边形中,与的平分线交于点,,则的度数是 .
14.如图,在五边形中,,,,则 .
三.解答题(共3小题)
15.一个正多边形的一个内角为,求这个多边形的内角和.
一个正多边形的一个内角减去其外角为,求这个正多边形的边数.
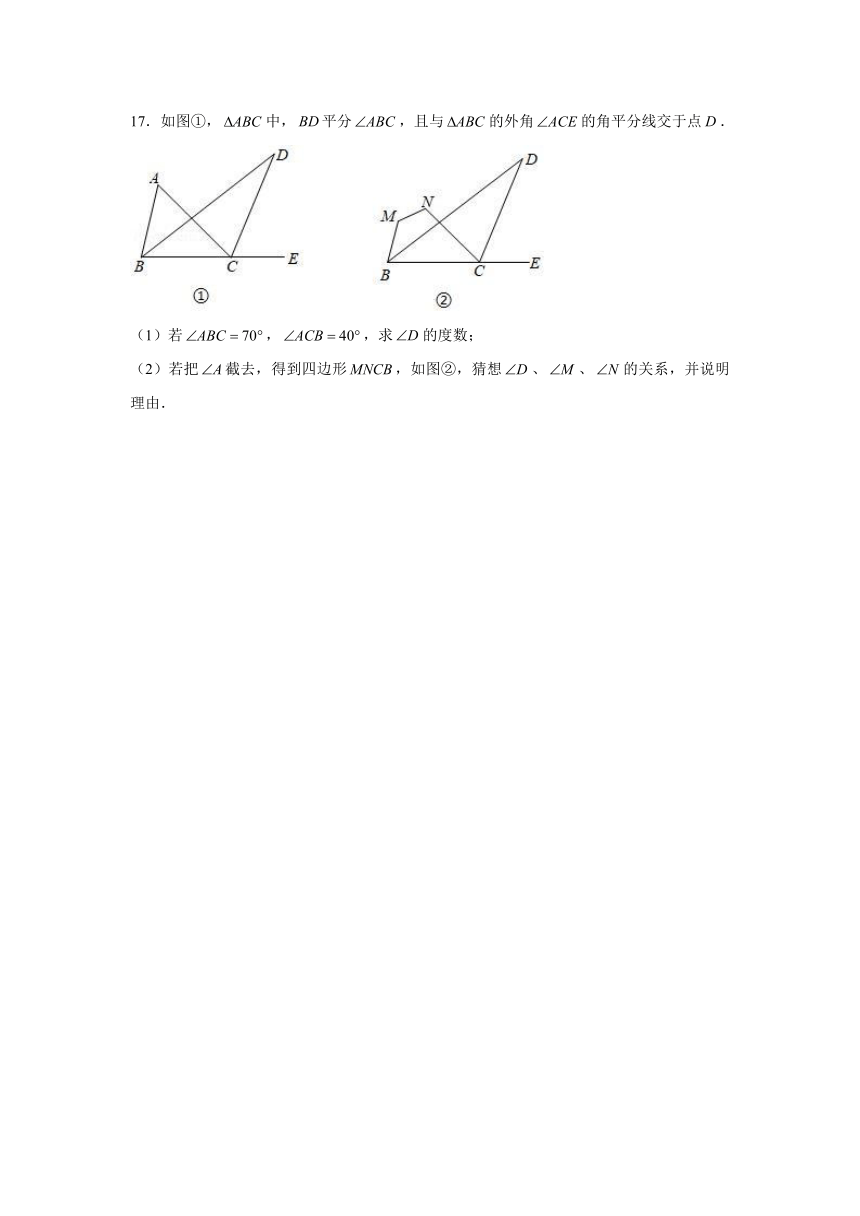
17.如图①,中,平分,且与的外角的角平分线交于点.
(1)若,,求的度数;
(2)若把截去,得到四边形,如图②,猜想、、的关系,并说明理由.
参考答案
选择题(共 10 小题)
题号 1 2 3 4 5 6 7 8 9 10
答案 B D A A A A B B C B
一.选择题(共10小题)
1.解:设所求多边形的边数为,根据题意得:
,
解得.
故选:.
2.解:因为多边形的外角和是,
又因为多边形的每个外角都是,
所以这个多边形的边数为:.
故选:.
3.解:设正多边形的边数为,由题意得:
,
解得:,
故选:.
4.解:,
(米,
故选:.
5.解:多边形的边数是:.
故选:.
6.解:正多边形的一个内角是,
它的外角是:,
.
即这个正多边形是九边形.
故选:.
7.解:五边形的内角都相等,
,
,
,
,
.
故选:.
8.解:在中,,
,
故选:.
9.解:如图,
,
,
,
.
故选:.
10.解:如图②,由折叠得:,
,
,,
,
,
,
由折叠得:如图③,,
,
故选:.
二.填空题(共4小题)
11.解:多边形的边数为:,
正多边形的内角和的度数是:.
故答案为:.
12.解:如图,延长、.
,
又,
.
,
.
故答案为:.
13.解:在五边形中,,
,
又、分别平分、,
,
中,.
故答案为:.
14.解:连接,
,
,
,,
,
,
故答案为:92.
三.解答题(共3小题)
15.解:正多边形的每个内角为,
正多边形的每个外角为,
多边形的外角和为,
多边形的边数为,
这个多边形的内角和是.
16.解:设一个内角为,则外角为,
,
解得,
则其外角为,
这个正多边形的边数为.
答:这个正多边形的边数为8.
17.解:(1),
,,
又平分,平分,
,,
,,
,
,,
,
;
(2);
理由:延长、交于点,
,,,
,
则,
由(1)知,,
.
多边形的内角和
多边形的内角和公式:n边形的内角和等于(n-2)×180°。
多边形的内角和推理方法
方法1:如图1所示,从n边形的一个顶点引出(n-3)条对角线,这(n-3)条对角线把n边形分成(n-2)个三角形,每个三角形的内角和是180°,所以n边形的内角和为(n-2)×180°。
方法2:如图2所示,在n边形内任取一点P,连接PA1,PA2……PAn,把n边形分成n个三角形,这n个三角形的内角和为n ×180°,再减去一个周角,即得n边形的内角和为n×180° -360°=(n-2)×180°。
方法3:如图3所示,如图所示,在n边形的 一边上任取一点P与各顶点相连,得(n-1)个三角形,n边形内角和等于这(n-1)个三角形的内角和减去在点P 处的一个平角,即得n边形的内角和为(n-1)×180° -180° =(n-2)×180°。
多边形的外角和
性质:多边形的外角和等于360°。
多边形的边数与内角和、外角和的关系
1、n边形的内角和等于(n-2)·180°(n≥3,n是正整数),可见多边形内角和与边数n有关,每增加1条边,内角和增加180°.
2、多边形的外角和等于360°,与边数的多少无关.
3、正n边形:正n边形的内角的度数为,外角的度数为.
一.选择题(共10小题)
1.下列多边形中,内角和与外角和相等的是
A. B.
C. D.
2.一个多边形每一个外角都等于,则这个多边形的边数为
A.12 B.14 C.16 D.18
3.一个正多边形的一个内角是其外角的3倍,则正多边形的边数为
A.8 B.9 C.10 D.12
4.如图,小明从点出发,沿直线前进8米后向左转,再沿直线前进8米,又向左转,,照这样走下去,他第一次回到出发点时,走过的总路程为
A.48米 B.80米 C.96米 D.无限长
5.如果一个多边形的每一个外角都是,那么这个多边形的边数是
A.12 B.13 C.14 D.15
6.已知正多边形的一个内角是,则这个正多边形的边数是
A.九边形 B.八边形 C.七边形 D.六边形
7.如图,五边形的内角都相等,且,,则
A. B. C. D.
8.如图,将四边形去掉一个的角得到一个五边形,则与的和为
A. B. C. D.
9.如图,的度数为
A. B. C. D.
10.如图,图1是一个四边形纸条,其中,,分别为边,上的两个点,将纸条沿折叠得到图2,再将图2沿折叠得到图3,若在图3中,,则的度数为
A. B. C. D.
二.填空题(共4小题)
11.已知一个正多边形的一个外角为,则它的内角和为 .
12.如图,,,是五边形的3个外角,若,则 .
13.如图,在五边形中,与的平分线交于点,,则的度数是 .
14.如图,在五边形中,,,,则 .
三.解答题(共3小题)
15.一个正多边形的一个内角为,求这个多边形的内角和.
一个正多边形的一个内角减去其外角为,求这个正多边形的边数.
17.如图①,中,平分,且与的外角的角平分线交于点.
(1)若,,求的度数;
(2)若把截去,得到四边形,如图②,猜想、、的关系,并说明理由.
参考答案
选择题(共 10 小题)
题号 1 2 3 4 5 6 7 8 9 10
答案 B D A A A A B B C B
一.选择题(共10小题)
1.解:设所求多边形的边数为,根据题意得:
,
解得.
故选:.
2.解:因为多边形的外角和是,
又因为多边形的每个外角都是,
所以这个多边形的边数为:.
故选:.
3.解:设正多边形的边数为,由题意得:
,
解得:,
故选:.
4.解:,
(米,
故选:.
5.解:多边形的边数是:.
故选:.
6.解:正多边形的一个内角是,
它的外角是:,
.
即这个正多边形是九边形.
故选:.
7.解:五边形的内角都相等,
,
,
,
,
.
故选:.
8.解:在中,,
,
故选:.
9.解:如图,
,
,
,
.
故选:.
10.解:如图②,由折叠得:,
,
,,
,
,
,
由折叠得:如图③,,
,
故选:.
二.填空题(共4小题)
11.解:多边形的边数为:,
正多边形的内角和的度数是:.
故答案为:.
12.解:如图,延长、.
,
又,
.
,
.
故答案为:.
13.解:在五边形中,,
,
又、分别平分、,
,
中,.
故答案为:.
14.解:连接,
,
,
,,
,
,
故答案为:92.
三.解答题(共3小题)
15.解:正多边形的每个内角为,
正多边形的每个外角为,
多边形的外角和为,
多边形的边数为,
这个多边形的内角和是.
16.解:设一个内角为,则外角为,
,
解得,
则其外角为,
这个正多边形的边数为.
答:这个正多边形的边数为8.
17.解:(1),
,,
又平分,平分,
,,
,,
,
,,
,
;
(2);
理由:延长、交于点,
,,,
,
则,
由(1)知,,
.
