旋转
图片预览





文档简介
(共24张PPT)
育才中学数学组
23.1图形的旋转
一、自学教材并填空
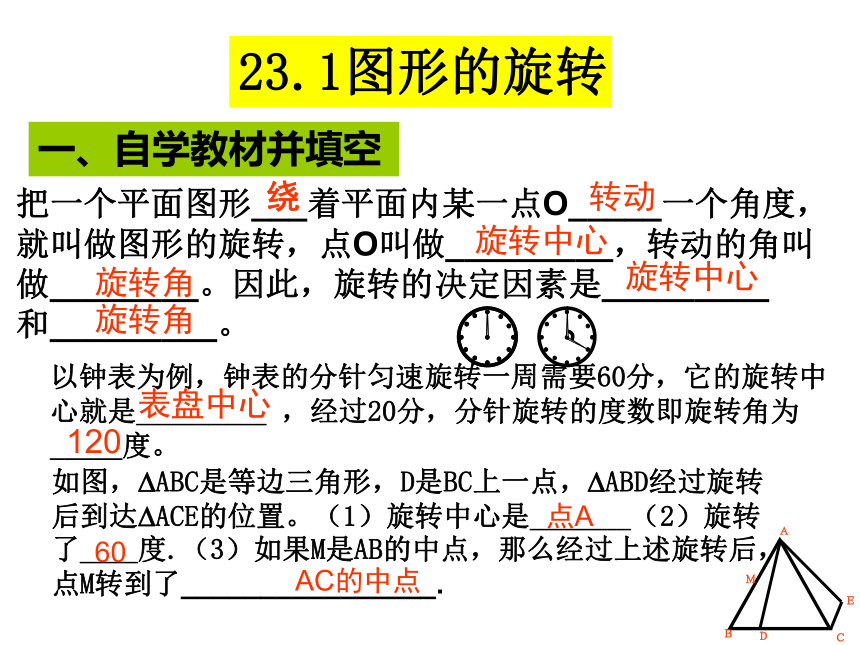
把一个平面图形___着平面内某一点O_____一个角度,
就叫做图形的旋转,点O叫做_________,转动的角叫
做________。因此,旋转的决定因素是_________
和_________。
绕
转动
旋转中心
旋转角
旋转中心
旋转角
以钟表为例,钟表的分针匀速旋转一周需要60分,它的旋转中心就是_________ ,经过20分,分针旋转的度数即旋转角为_____度。
表盘中心
120
如图, ABC是等边三角形,D是BC上一点, ABD经过旋转
后到达 ACE的位置。(1)旋转中心是_______(2)旋转
了____度.(3)如果M是AB的中点,那么经过上述旋转后,点M转到了________________.
E
D
C
B
A
M
点A
60
AC的中点
二、旋转的性质
1、对应点到旋转中心的距离相等;
2、对应点与旋转中心所连线段的夹角等于旋转角;
3、旋转前、后的两图形全等。
三、旋转的应用
1、已知△ABC是直角三角形,∠ACB=90°,AB=5㎝,BC=3厘米,△ABC绕点C逆时针方向旋转90°后得到△DEC,则∠D=______,
∠B=_____ _,DE=_______㎝,EC=______㎝,AE=_______㎝,DE与AB的位置关系为_________________.
2、正方形ABCD中有一点P,把△ABP绕点点B旋转到△CQB,连结PQ,则△PBQ的形状是_____________________________.
∠A
∠CED
5
3
1
互相垂直
等腰直角三角形
四、当堂检测题
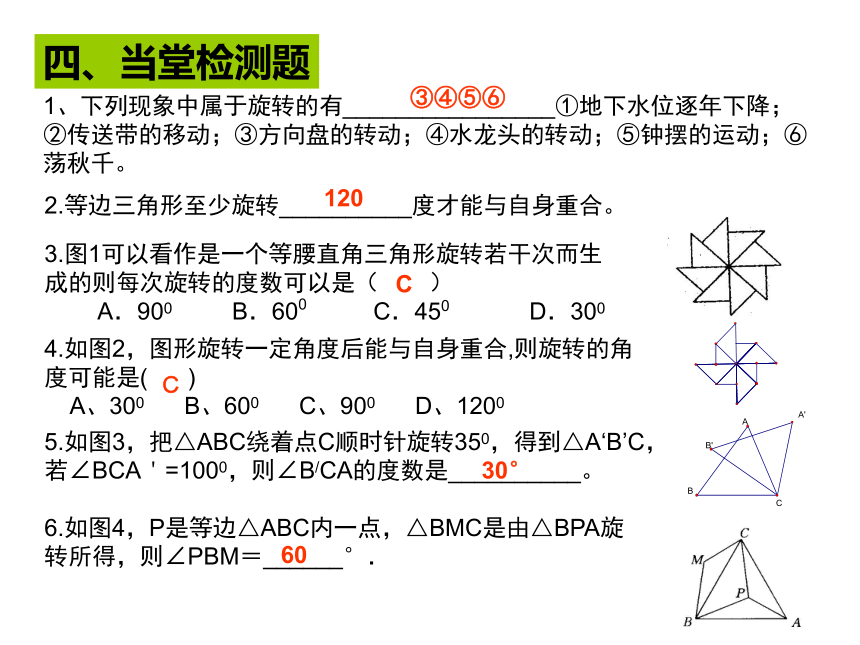
1、下列现象中属于旋转的有________________①地下水位逐年下降;②传送带的移动;③方向盘的转动;④水龙头的转动;⑤钟摆的运动;⑥荡秋千。
2.等边三角形至少旋转__________度才能与自身重合。
3.图1可以看作是一个等腰直角三角形旋转若干次而生
成的则每次旋转的度数可以是( )
A.900 B.600 C.450 D.300
5.如图3,把△ABC绕着点C顺时针旋转350,得到△A‘B’C,
若∠BCA'=1000,则∠B/CA的度数是__________。
4.如图2,图形旋转一定角度后能与自身重合,则旋转的角
度可能是( )
A、300 B、600 C、900 D、1200
6.如图4,P是等边△ABC内一点,△BMC是由△BPA旋
转所得,则∠PBM=______°.
③④⑤⑥
120
C
C
30°
60
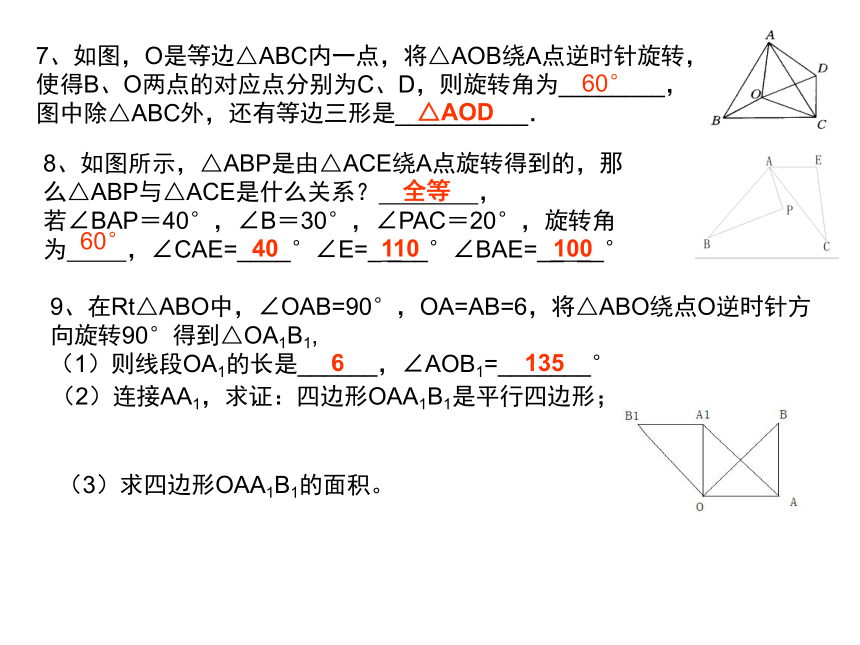
7、如图,O是等边△ABC内一点,将△AOB绕A点逆时针旋转,
使得B、O两点的对应点分别为C、D,则旋转角为________,
图中除△ABC外,还有等边三形是__________.
8、如图所示,△ABP是由△ACE绕A点旋转得到的,那么△ABP与△ACE是什么关系? ,
若∠BAP=40°,∠B=30°,∠PAC=20°,旋转角为 ,∠CAE=____°∠E=_ ___°∠BAE=__ __°
9、在Rt△ABO中,∠OAB=90°,OA=AB=6,将△ABO绕点O逆时针方向旋转90°得到△OA1B1,
(1)则线段OA1的长是______,∠AOB1=_______°
(2)连接AA1,求证:四边形OAA1B1是平行四边形;
(3)求四边形OAA1B1的面积。
60°
△AOD
全等
60°
40
110
100
6
135
23.2 中心对称
中心对称与中心对称图形
一、中心对称
1、定义:
把一个图形绕着某一个点旋转180°,如果它能够与另一个图形
重合,那么这两个图形关于这个点对称或中心对称。
其中这个点叫做对称中心;
这两个图形的对应点叫做关于中心的对称点。
注:
(1)关于中心对称的图形有两个;
(2)中心对称是把一个图形绕某一点旋转180°;
(3)中心对称揭示的是两个图形的一种位置关系。
2、性质:
(1)关于中心对称的两个图形,对称点所连线段都过
对称中心,而且被对称中心所平分;
(2)关于中心对称的两个图形是全等图形;
(3)关于中心对称的两个图形的对应线段平行(共线)且相等;
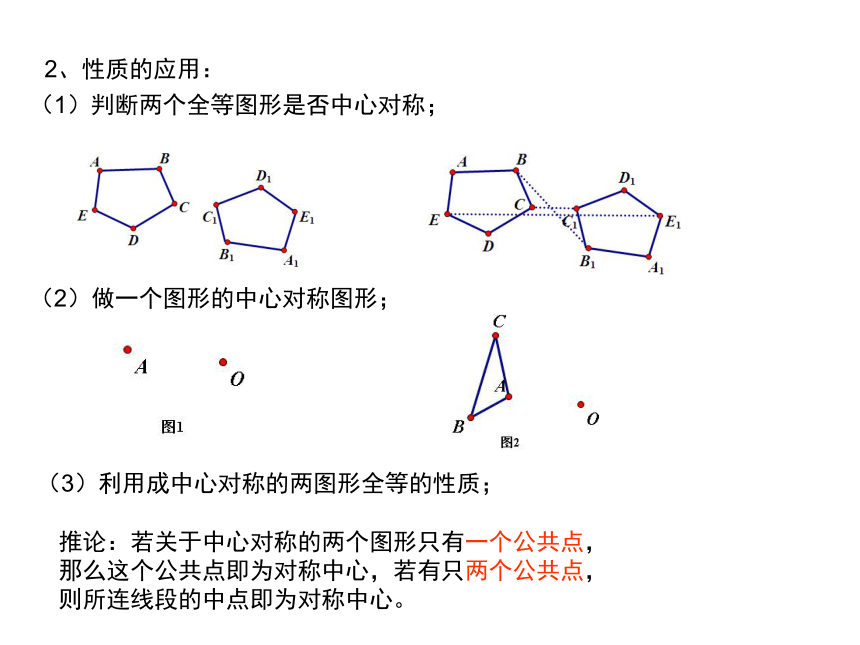
2、性质的应用:
(1)判断两个全等图形是否中心对称;
(2)做一个图形的中心对称图形;
推论:若关于中心对称的两个图形只有一个公共点,
那么这个公共点即为对称中心,若有只两个公共点,
则所连线段的中点即为对称中心。
(3)利用成中心对称的两图形全等的性质;
3、轴对称与中心对称
定义三要点
性 质
1 2 3
有一条轴对称——直线
图形沿轴对折,即翻转180°
翻转后与另一图形重合
1 2 3
轴 对 称
两个图形是全等形
对称轴是对应点连线的垂直平分线
对应线段或延长线相交时,交点在
对称轴上
中心对称
有一个对称中心——点
图形绕中心旋转180°
旋转后与另一图形重合
两个图形是全等形
对称点连线都经过对称中心,并且被
对称中心平分
对应线段平行(共线)且相等
二、中心对称图形
1、定义:
把一个图形绕着某一个点旋转180°,如果旋转后的图形能够与原
来的图形重合,那么这个图形叫做中心对称图形。
这个点叫做这个图形的对称中心。
注:
(1)中心对称图形是一个图形本身的特征;
(2)中心对称图形是本身围绕一点旋转180°;
(3)旋转后的图形与原来的图形重合。
3、常见的中心对称图形
线段、
平行四边形(矩形、菱形、正方形)、
圆、
正偶边形 等
(1)对称中心平分中心对称图形内通过该点的任意线段且使中心对称图形的面积被平分
2、性质:
(2)中心对称图形上每一对对称点所连成的线段都被对称中心平分 ;
名称 中心对称 中心对称图形
区别 1、
2、
联系
4、中心对称与中心对称图形
5、轴对称图形与中心对称图形
两者在定义与性质上都有明显的区别,大家知道,轴对称图形的对称轴可以有多条,那么中心对称图形的对称中心可能有多个还是只有一个呢?请举例说明。
若将中心对称的两个图形看做一个整体,那么这个图形就是一个中心对称图形;若将一个中心对称图形用过对称中心的任意一条直线分成两部分,则这两部分关于这点成中心对称。
两个图形
一个图形
两图形相互位置关系
一图形本身的特征
三、课后规范化作业
1、关于中心对称的两个图形,对应线段的关系是( ). (A) 平行 (B) 相等 (C) 平行且相等 (D) 相等且平行或在同一直线上
2、关于中心对称的两个图形,对称点的连线____________
3、 如果两个图形的对应点连成的线段都经过某一点,并且被平分,则这
两个图形一定关于这一点成____________对称.
4、ΔABC和ΔA’B’C’关于点O中心对称,若ΔABC的周长为12cm,ΔA’B’C’
的面积为6cm2,则ΔA’B’C’的周长为_________,ΔABC的面积为_______。
5、 如图所示,△ABO与△CDO关于点O成中心对称,则在一
直线上的三点有 ,并且AO= ,BO= .
6、 已知A、B、O三点不共线,A、A’关于O对称,B、B’关于O对称,那
么线段AB与A’B’的关系____ ____.
7、已知点O是平行四边形 ABCD对角线的交点,则图中关于点O对称的三角形
有_____对,它们分别是____________________________ _______________.
D
被对称中心平分
中心
12cm
6cm2
A、O、C与B、O、D
CO
DO
平行且相等
4
ΔAOB与ΔCOD、
ΔAOD与ΔCOB、
ΔABD与ΔCDB、
ΔABC与ΔCDA
8、右图中②③④⑤分别由①图顺时针旋转180°变
换而成的是____________。
三、课后规范化作业
9、如下图中,既是中心对称又是轴对称的图案是( ).
A B C D
10、欣赏右上图的图案,它们中间中心对称图形的个数有 个.
11、如图,在矩形ABCD中,对角线交于点O,过点O的直线交
AD与BC于点E、F,AB=2,BC=3,则图中阴影部分的面积是____.
12、已知点O是四边形ABCD的对称中心,
求证:四边形ABCD是平行四边形。
③
C
3
3
课间思考:
如图,线段AB绕点O进行旋转至A1B1,旋转角为
α(0°<α<180°),若将两线段向两端适当延长,
则会相交形成四个角,设最小的角大小为β,试猜想α
与β之间的数量关系,不要求证明。
1.点M(-3,-4)在第___象限,点M到x轴的距离是_____,到Y轴的距离是_____,到原点的距离是______.
2.点P(2,3)关于x轴的对称点的坐标_________关于Y轴的对称点的坐标是_____________.
(2,-3)
(-2,3)
三
4
3
5
关于原点对称的点的坐标
3、关于坐标轴对称的点的坐标变化规律
关于哪个轴对称,哪个坐标就不“变”
y
x
A
B
C
D
E
F
5
-5
-2
-3
-4
-1
3
2
4
1
-5
5
-3
-4
4
-2
3
-1
2
1
o
如图,在直角坐标系中,已知A 、 B 、
C 、 D 、E 、F ,作出A、B、C、D、E、F点关于原点O的中心对称点,并写出它们的坐标,并回答:这些坐标与已知点的坐标有什么关系?
(0,3)
(-3,1)
(-4,0)
(2,2)
(3,-3)
(-2,-2)
☆探究
☆讨论交流归纳
分组讨论、交流:
讨论的内容:关于原点作中心对称时,
①它们的横坐标与横坐标的绝对值有什么关系?纵坐标与纵坐标的绝对值又有什么关系?
②坐标与坐标之间符号又有什么特点?
两个点关于原点对称时,它们的坐标符号相反,
即点P(x,y)关于原点O的对称点
(-x,-y).
☆归纳
两个点关于原点对称时,它们的坐标符号相反,
即点P(x,y)关于原点O的对称点P/(-x,-y).
☆练一练
1.如果点P(-3,1),那么点P(-3,1)关于原点
的对称点 的坐标是_______.
(3, - 1)
点A和H;
点B和I;
点C和F;
如图,利用关于原点对称的点的坐标的特点,作出与线段AB关于原点对称的图形.
☆例题精析
B′
A′
解:
☆练习巩固
1.已知△ABC在平面直角坐标系上三顶点坐标为
A(-2,3),B(-1,1),C(-3,2),△A1B1C1与△ABC关于原点对称,则A1(____),B1(_ ),C1(_______).
2.如果点M(1-x,1-y)在第二象限,那么点N(1-x,y-1)关于原点的对称点在第__象限.
3.已知点P到x轴的距离为2,到y轴的距离为3,则点P关于原点的对称点P′坐标为_________.
☆达标检测
4.若点P(x,-3)与点Q(4,y)关于原点对称,则x+y等于( )
A.1 B.-1 C.7 D.-7
5.已知点A(2,2),如果点A关于x轴的对称点是B,B点关于原点的对称点为C,那么C点的坐标是( )
A(2,2) B(-2,2) C(2,-2) D(-2,-2)
6.将平面直角坐标系内某图形上各个点的纵横坐标都乘-1,所得图形与原图形的关系是( )
A.关于x轴对称 B.关于y轴对称
C.关于原点对称 D.位置不变
7、如图,直线AB与x轴、y轴分别相交于A、B两点,将直线AB绕点O顺时针旋转90°得到直线A1B1.
(1)在图中画出直线A1B1.
(2)求出直线A1B1的函数解析式
8.如图,在平面直角坐标系中,A(-3,1),B(-2,3),C(0,2),画出△ABC关于x轴对称的△A′B′C′,再画出△A′B′C′关于y轴对称的△A″B″C″,那么△A″B″C″与△ABC有什么关系,请说明理由.
小结
本节课你学会了什么
育才中学数学组
23.1图形的旋转
一、自学教材并填空
把一个平面图形___着平面内某一点O_____一个角度,
就叫做图形的旋转,点O叫做_________,转动的角叫
做________。因此,旋转的决定因素是_________
和_________。
绕
转动
旋转中心
旋转角
旋转中心
旋转角
以钟表为例,钟表的分针匀速旋转一周需要60分,它的旋转中心就是_________ ,经过20分,分针旋转的度数即旋转角为_____度。
表盘中心
120
如图, ABC是等边三角形,D是BC上一点, ABD经过旋转
后到达 ACE的位置。(1)旋转中心是_______(2)旋转
了____度.(3)如果M是AB的中点,那么经过上述旋转后,点M转到了________________.
E
D
C
B
A
M
点A
60
AC的中点
二、旋转的性质
1、对应点到旋转中心的距离相等;
2、对应点与旋转中心所连线段的夹角等于旋转角;
3、旋转前、后的两图形全等。
三、旋转的应用
1、已知△ABC是直角三角形,∠ACB=90°,AB=5㎝,BC=3厘米,△ABC绕点C逆时针方向旋转90°后得到△DEC,则∠D=______,
∠B=_____ _,DE=_______㎝,EC=______㎝,AE=_______㎝,DE与AB的位置关系为_________________.
2、正方形ABCD中有一点P,把△ABP绕点点B旋转到△CQB,连结PQ,则△PBQ的形状是_____________________________.
∠A
∠CED
5
3
1
互相垂直
等腰直角三角形
四、当堂检测题
1、下列现象中属于旋转的有________________①地下水位逐年下降;②传送带的移动;③方向盘的转动;④水龙头的转动;⑤钟摆的运动;⑥荡秋千。
2.等边三角形至少旋转__________度才能与自身重合。
3.图1可以看作是一个等腰直角三角形旋转若干次而生
成的则每次旋转的度数可以是( )
A.900 B.600 C.450 D.300
5.如图3,把△ABC绕着点C顺时针旋转350,得到△A‘B’C,
若∠BCA'=1000,则∠B/CA的度数是__________。
4.如图2,图形旋转一定角度后能与自身重合,则旋转的角
度可能是( )
A、300 B、600 C、900 D、1200
6.如图4,P是等边△ABC内一点,△BMC是由△BPA旋
转所得,则∠PBM=______°.
③④⑤⑥
120
C
C
30°
60
7、如图,O是等边△ABC内一点,将△AOB绕A点逆时针旋转,
使得B、O两点的对应点分别为C、D,则旋转角为________,
图中除△ABC外,还有等边三形是__________.
8、如图所示,△ABP是由△ACE绕A点旋转得到的,那么△ABP与△ACE是什么关系? ,
若∠BAP=40°,∠B=30°,∠PAC=20°,旋转角为 ,∠CAE=____°∠E=_ ___°∠BAE=__ __°
9、在Rt△ABO中,∠OAB=90°,OA=AB=6,将△ABO绕点O逆时针方向旋转90°得到△OA1B1,
(1)则线段OA1的长是______,∠AOB1=_______°
(2)连接AA1,求证:四边形OAA1B1是平行四边形;
(3)求四边形OAA1B1的面积。
60°
△AOD
全等
60°
40
110
100
6
135
23.2 中心对称
中心对称与中心对称图形
一、中心对称
1、定义:
把一个图形绕着某一个点旋转180°,如果它能够与另一个图形
重合,那么这两个图形关于这个点对称或中心对称。
其中这个点叫做对称中心;
这两个图形的对应点叫做关于中心的对称点。
注:
(1)关于中心对称的图形有两个;
(2)中心对称是把一个图形绕某一点旋转180°;
(3)中心对称揭示的是两个图形的一种位置关系。
2、性质:
(1)关于中心对称的两个图形,对称点所连线段都过
对称中心,而且被对称中心所平分;
(2)关于中心对称的两个图形是全等图形;
(3)关于中心对称的两个图形的对应线段平行(共线)且相等;
2、性质的应用:
(1)判断两个全等图形是否中心对称;
(2)做一个图形的中心对称图形;
推论:若关于中心对称的两个图形只有一个公共点,
那么这个公共点即为对称中心,若有只两个公共点,
则所连线段的中点即为对称中心。
(3)利用成中心对称的两图形全等的性质;
3、轴对称与中心对称
定义三要点
性 质
1 2 3
有一条轴对称——直线
图形沿轴对折,即翻转180°
翻转后与另一图形重合
1 2 3
轴 对 称
两个图形是全等形
对称轴是对应点连线的垂直平分线
对应线段或延长线相交时,交点在
对称轴上
中心对称
有一个对称中心——点
图形绕中心旋转180°
旋转后与另一图形重合
两个图形是全等形
对称点连线都经过对称中心,并且被
对称中心平分
对应线段平行(共线)且相等
二、中心对称图形
1、定义:
把一个图形绕着某一个点旋转180°,如果旋转后的图形能够与原
来的图形重合,那么这个图形叫做中心对称图形。
这个点叫做这个图形的对称中心。
注:
(1)中心对称图形是一个图形本身的特征;
(2)中心对称图形是本身围绕一点旋转180°;
(3)旋转后的图形与原来的图形重合。
3、常见的中心对称图形
线段、
平行四边形(矩形、菱形、正方形)、
圆、
正偶边形 等
(1)对称中心平分中心对称图形内通过该点的任意线段且使中心对称图形的面积被平分
2、性质:
(2)中心对称图形上每一对对称点所连成的线段都被对称中心平分 ;
名称 中心对称 中心对称图形
区别 1、
2、
联系
4、中心对称与中心对称图形
5、轴对称图形与中心对称图形
两者在定义与性质上都有明显的区别,大家知道,轴对称图形的对称轴可以有多条,那么中心对称图形的对称中心可能有多个还是只有一个呢?请举例说明。
若将中心对称的两个图形看做一个整体,那么这个图形就是一个中心对称图形;若将一个中心对称图形用过对称中心的任意一条直线分成两部分,则这两部分关于这点成中心对称。
两个图形
一个图形
两图形相互位置关系
一图形本身的特征
三、课后规范化作业
1、关于中心对称的两个图形,对应线段的关系是( ). (A) 平行 (B) 相等 (C) 平行且相等 (D) 相等且平行或在同一直线上
2、关于中心对称的两个图形,对称点的连线____________
3、 如果两个图形的对应点连成的线段都经过某一点,并且被平分,则这
两个图形一定关于这一点成____________对称.
4、ΔABC和ΔA’B’C’关于点O中心对称,若ΔABC的周长为12cm,ΔA’B’C’
的面积为6cm2,则ΔA’B’C’的周长为_________,ΔABC的面积为_______。
5、 如图所示,△ABO与△CDO关于点O成中心对称,则在一
直线上的三点有 ,并且AO= ,BO= .
6、 已知A、B、O三点不共线,A、A’关于O对称,B、B’关于O对称,那
么线段AB与A’B’的关系____ ____.
7、已知点O是平行四边形 ABCD对角线的交点,则图中关于点O对称的三角形
有_____对,它们分别是____________________________ _______________.
D
被对称中心平分
中心
12cm
6cm2
A、O、C与B、O、D
CO
DO
平行且相等
4
ΔAOB与ΔCOD、
ΔAOD与ΔCOB、
ΔABD与ΔCDB、
ΔABC与ΔCDA
8、右图中②③④⑤分别由①图顺时针旋转180°变
换而成的是____________。
三、课后规范化作业
9、如下图中,既是中心对称又是轴对称的图案是( ).
A B C D
10、欣赏右上图的图案,它们中间中心对称图形的个数有 个.
11、如图,在矩形ABCD中,对角线交于点O,过点O的直线交
AD与BC于点E、F,AB=2,BC=3,则图中阴影部分的面积是____.
12、已知点O是四边形ABCD的对称中心,
求证:四边形ABCD是平行四边形。
③
C
3
3
课间思考:
如图,线段AB绕点O进行旋转至A1B1,旋转角为
α(0°<α<180°),若将两线段向两端适当延长,
则会相交形成四个角,设最小的角大小为β,试猜想α
与β之间的数量关系,不要求证明。
1.点M(-3,-4)在第___象限,点M到x轴的距离是_____,到Y轴的距离是_____,到原点的距离是______.
2.点P(2,3)关于x轴的对称点的坐标_________关于Y轴的对称点的坐标是_____________.
(2,-3)
(-2,3)
三
4
3
5
关于原点对称的点的坐标
3、关于坐标轴对称的点的坐标变化规律
关于哪个轴对称,哪个坐标就不“变”
y
x
A
B
C
D
E
F
5
-5
-2
-3
-4
-1
3
2
4
1
-5
5
-3
-4
4
-2
3
-1
2
1
o
如图,在直角坐标系中,已知A 、 B 、
C 、 D 、E 、F ,作出A、B、C、D、E、F点关于原点O的中心对称点,并写出它们的坐标,并回答:这些坐标与已知点的坐标有什么关系?
(0,3)
(-3,1)
(-4,0)
(2,2)
(3,-3)
(-2,-2)
☆探究
☆讨论交流归纳
分组讨论、交流:
讨论的内容:关于原点作中心对称时,
①它们的横坐标与横坐标的绝对值有什么关系?纵坐标与纵坐标的绝对值又有什么关系?
②坐标与坐标之间符号又有什么特点?
两个点关于原点对称时,它们的坐标符号相反,
即点P(x,y)关于原点O的对称点
(-x,-y).
☆归纳
两个点关于原点对称时,它们的坐标符号相反,
即点P(x,y)关于原点O的对称点P/(-x,-y).
☆练一练
1.如果点P(-3,1),那么点P(-3,1)关于原点
的对称点 的坐标是_______.
(3, - 1)
点A和H;
点B和I;
点C和F;
如图,利用关于原点对称的点的坐标的特点,作出与线段AB关于原点对称的图形.
☆例题精析
B′
A′
解:
☆练习巩固
1.已知△ABC在平面直角坐标系上三顶点坐标为
A(-2,3),B(-1,1),C(-3,2),△A1B1C1与△ABC关于原点对称,则A1(____),B1(_ ),C1(_______).
2.如果点M(1-x,1-y)在第二象限,那么点N(1-x,y-1)关于原点的对称点在第__象限.
3.已知点P到x轴的距离为2,到y轴的距离为3,则点P关于原点的对称点P′坐标为_________.
☆达标检测
4.若点P(x,-3)与点Q(4,y)关于原点对称,则x+y等于( )
A.1 B.-1 C.7 D.-7
5.已知点A(2,2),如果点A关于x轴的对称点是B,B点关于原点的对称点为C,那么C点的坐标是( )
A(2,2) B(-2,2) C(2,-2) D(-2,-2)
6.将平面直角坐标系内某图形上各个点的纵横坐标都乘-1,所得图形与原图形的关系是( )
A.关于x轴对称 B.关于y轴对称
C.关于原点对称 D.位置不变
7、如图,直线AB与x轴、y轴分别相交于A、B两点,将直线AB绕点O顺时针旋转90°得到直线A1B1.
(1)在图中画出直线A1B1.
(2)求出直线A1B1的函数解析式
8.如图,在平面直角坐标系中,A(-3,1),B(-2,3),C(0,2),画出△ABC关于x轴对称的△A′B′C′,再画出△A′B′C′关于y轴对称的△A″B″C″,那么△A″B″C″与△ABC有什么关系,请说明理由.
小结
本节课你学会了什么
同课章节目录
