8.1 平均数（一）导学案（无答案）

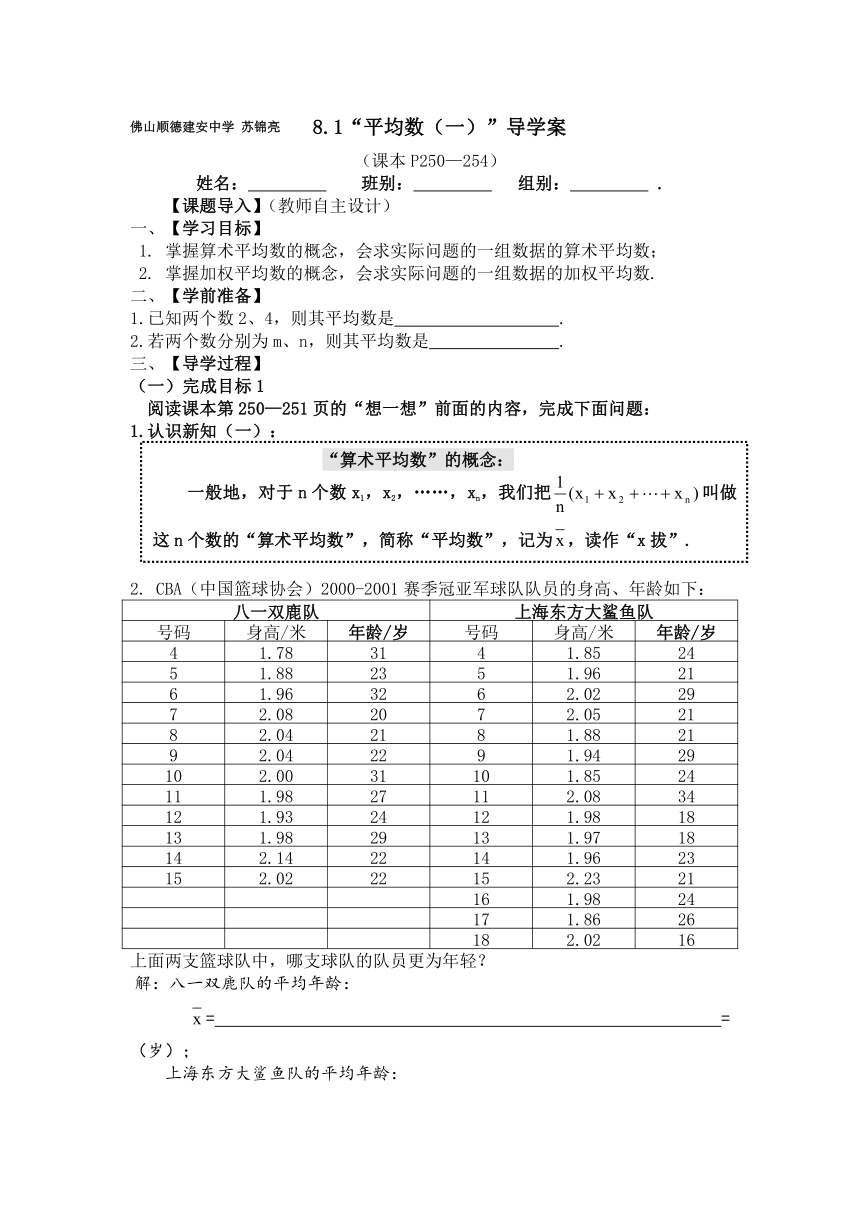
佛山顺德建安中学 苏锦亮 8.1“平均数（一）”导学案
（课本P250—254）
姓名： 班别： 组别： .
【课题导入】（教师自主设计）
一、【学习目标】
1. 掌握算术平均数的概念，会求实际问题的一组数据的算术平均数；
2. 掌握加权平均数的概念，会求实际问题的一组数据的加权平均数.
二、【学前准备】
1.已知两个数2、4，则其平均数是 .
2.若两个数分别为m、n，则其平均数是 .
三、【导学过程】
（一）完成目标1
阅读课本第250—251页的“想一想”前面的内容，完成下面问题：
1.认识新知（一）：
2. CBA（中国篮球协会）2000-2001赛季冠亚军球队队员的身高、年龄如下：
八一双鹿队 上海东方大鲨鱼队
号码 身高/米 年龄/岁 号码 身高/米 年龄/岁
4 1.78 31 4 1.85 24
5 1.88 23 5 1.96 21
6 1.96 32 6 2.02 29
7 2.08 20 7 2.05 21
8 2.04 21 8 1.88 21
9 2.04 22 9 1.94 29
10 2.00 31 10 1.85 24
11 1.98 27 11 2.08 34
12 1.93 24 12 1.98 18
13 1.98 29 13 1.97 18
14 2.14 22 14 1.96 23
15 2.02 22 15 2.23 21
16 1.98 24
17 1.86 26
18 2.02 16
上面两支篮球队中，哪支球队的队员更为年轻？
解：八一双鹿队的平均年龄：
= = （岁）；
上海东方大鲨鱼队的平均年龄：
= = （岁）.
∵ 的平均年龄最小. ∴ 球队的队员更为年轻.
【交流评价1：小组内交流，互评对错，并帮助改正，分析错误原因，加以总结。共性的问题全班交流】
（一）完成目标2
阅读课本第251页“想一想”---第253页的内容，完成下面问题：
1.为了更方便计算东方大鲨鱼队队员的平均年龄，小明用了下面的计算方法，你理解他这样做的道理吗？
年龄/岁 16 18 21 23 24 26 29 34
相应队员数 1 2 4 1 3 1 2 1
解：
= （岁）
答：东方大鲨鱼队队员的平均年龄是 岁.
2.认识新知（二）：
3.某广告公司招聘广告策划人员一名，对A、B、C三名候选人进行了三项素质测试，他们的各项测试成绩如下表所示：
测试项目 测试成绩
A B C
创新 72 85 67
综合知识 50 74 70
语言 88 45 67
（1）如果根据三项测试的平均成绩确定采用人选，那么谁将被录用？
解：〈提示：按算术平均数公式算〉
A的平均成绩为（72+ + ）=× = （分）；
B的平均成绩为（85+ + ）=× = （分）；
C的平均成绩为（67+ + ）=× = （分）.
∵ 的算术平均成绩最高.
∴ 候选人 将被录用.
（2）据实际需要，公司将创新、综合知识和语言三项测试得分按4：3：1的比例确定各人的测试成绩，此时谁将被录用？
解：〈提示：按加权平均数公式算〉
A的平均成绩为 （分）；
B的平均成绩为 = （分）；
C的平均成绩为 = （分）.
∵ 的加权平均成绩最高.
∴ 候选人 将被录用.
【交流评价2：小组内交流，互评对错，并帮助改正，分析错误原因，加以总结。共性的问题全班交流】
四、【自我小结】
通过本节课的学习，你有哪些收获？（包括知识的、方法的）
五、【达标检测】
（一）基础知识过关：
1．某人今年1至5月的电话费数据如下（单位：元）：60，68，78，66，68，这组数据的平均数数是（　　）
A．66 B．67 C．68 D．78
2.如果将一组数据的每一个数据扩大2倍，那么平均数 （ ）
A. 不变 B. 扩大2倍 C. 缩小2倍 D.无法确定
3.8名同学在一次数学测试中的成绩为80、82、69、74、78、x、81，这组数的平均数是77，则x的值是( )
A. 76 B. 75 C. 74 D. 73
4.要了解某地农民用电情况,抽查了部分农民在一个月中用电情况,其中用电15度有3户,用电20度有5户,用电30度有7户,那么平均每户用电 ( )
A. 23.7度 B. 21.6度 C. 20度 D. 5.416度
5.某次体操比赛，六位评委对某选手的打分如下(单位：分)：
9.5， 9.3， 9.1， 9.5， 9.4， 9.3
(1)求这六个分数的平均分；
(2)如果规定：去掉一个最高分和一个最低分，余下的平均值作为选手的最后得分，那么该选手的最后得分是多少？
6.某人在一次应聘中，笔试成绩98分，面试成绩90分，形象分90分，招聘单位
按笔试、面试、形象5:3:2的比例统分，那么他的最后得分是多少？
7.为了考察甲、乙两种作物的长势，研究人员分别抽取了10株苗，测得他们的高度如下(单位：cm)：甲：9，14，11，12，9，13，10，8，12，8；
乙：8，13，12，11，9，12， 7， 7， 9，11。
你认为哪种农作物长得高一些？说说理由。
（二）能力提升：
8.八年级一班有学生50人，八年级二班有学生45人.期末数学测试中，一班学生的平均分为81.5分，二班学生的平均分为83.4分，那么两个班95名学生的平均分是多少？
9.某灯泡厂为了测定本厂生产的灯泡的使用寿命(单位：时)，从中抽查了400只灯泡，测得它们的使用寿命如下：
使用寿命/时 500~600 600~700 700~800 800~900 900~1000 1000~1100
灯泡数 21 79 108 92 76 24
为了计算方便，使用寿命介于500时与600时之间的灯泡的使用寿命均近似地看作550时……使用寿命介于1000时与1100时之间的灯泡的使用寿命均近似地看作1050时，这400只灯泡的平均使用寿命约是 时.
六、【学习后记】
七、【家长的话，并签名】
家长签名： .
“算术平均数”的概念：
一般地，对于n个数x1，x2，……，xn，我们把叫做这n个数的“算术平均数”，简称“平均数”，记为，读作“x拔”.
答案与上面的一样吗？你理解吗？
“算术平均数”的概念：
（1）在实际问题中，一组数据里的各个数据的“重要程度”未必相同。因而，在计算这组数据的平均数时，往往给每个数据一个“权”。如上题中1、2、4、1、3、1、2、1分别是年龄16、18、21、23、24、26、29、34的权，这样算出来的平均数称为东方大鲨鱼队队员的年龄的“加权平均数”.
（2）加权平均数，其中叫做权.