4.8图形的位似同步练习-2021-2022学年北师大版数学九年级上册(Word版 含答案)
文档属性
| 名称 | 4.8图形的位似同步练习-2021-2022学年北师大版数学九年级上册(Word版 含答案) |  | |
| 格式 | docx | ||
| 文件大小 | 170.4KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-10-19 14:31:11 | ||
图片预览

文档简介
4.8图形的位似
一.选择题
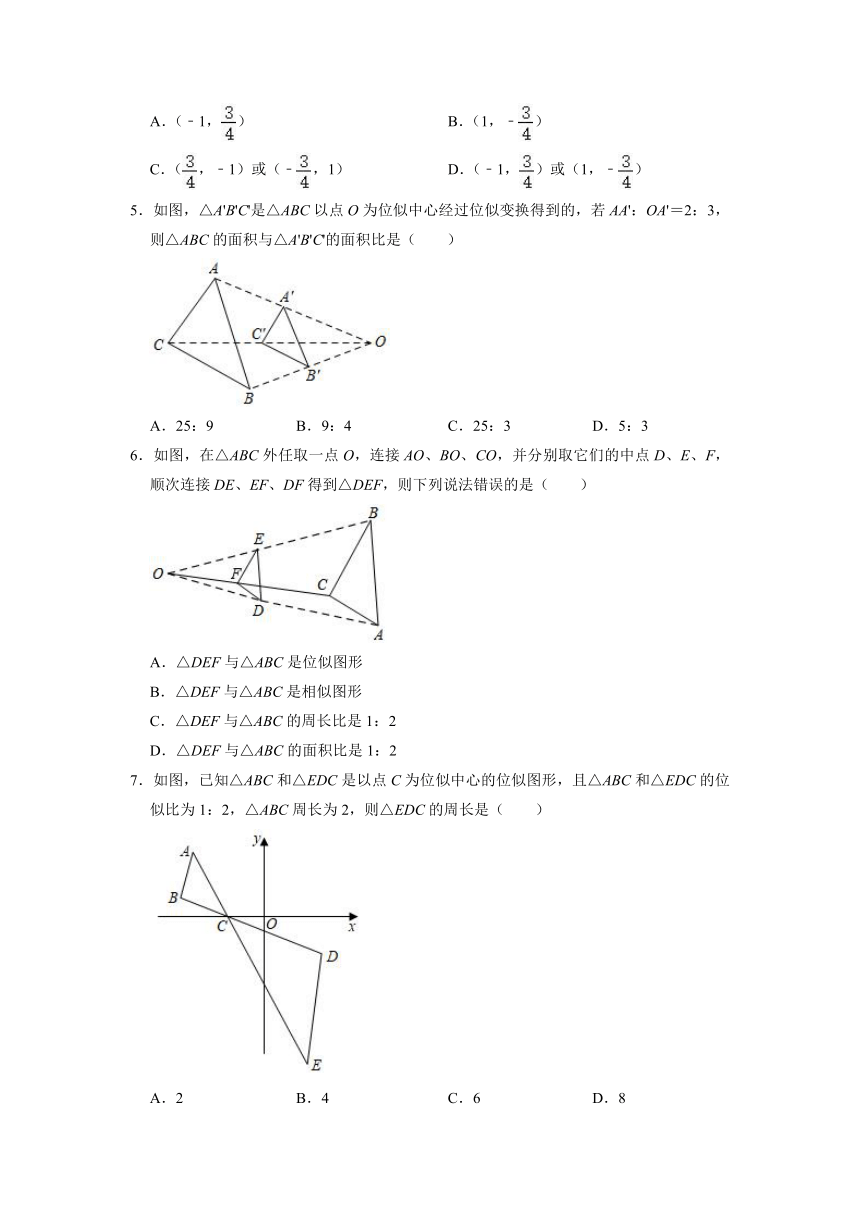
1.如图,BC∥ED,下列说法不正确的是( )
A.两个三角形是位似图形
B.点A是两个三角形的位似中心
C.点B与点D、点C与点E是对应位似点
D.AC:AB是相似比
2.在下列四个三角形中,以O为位似中心且与△ABC位似的图形序号是( )
A.① B.② C.③ D.④
3.如图,△ABC与△A1B1C1位似,位似中心是点O,若OA:OA1=1:2,则△ABC与△A1B1C1的周长比是( )
A.1:2 B.1:3 C.1:4 D.1:
4.已知点A(0,3),B(﹣4,3),以原点O为位似中心,把线段AB缩短为原来的,其中点C与点A对应,点D与点B对应.则点D的坐标为( )
A.(﹣1,) B.(1,﹣)
C.(,﹣1)或(﹣,1) D.(﹣1,)或(1,﹣)
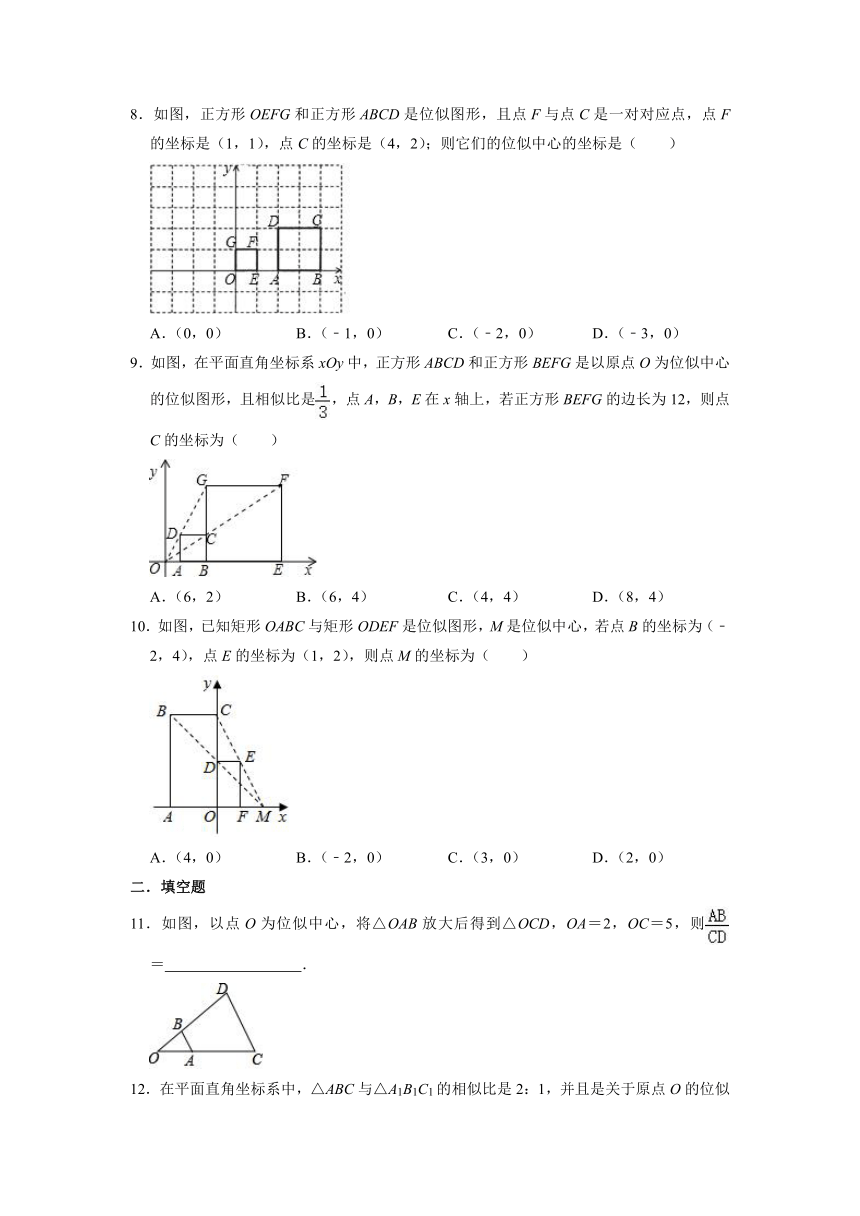
5.如图,△A'B'C'是△ABC以点O为位似中心经过位似变换得到的,若AA':OA'=2:3,则△ABC的面积与△A'B'C'的面积比是( )
A.25:9 B.9:4 C.25:3 D.5:3
6.如图,在△ABC外任取一点O,连接AO、BO、CO,并分别取它们的中点D、E、F,顺次连接DE、EF、DF得到△DEF,则下列说法错误的是( )
A.△DEF与△ABC是位似图形
B.△DEF与△ABC是相似图形
C.△DEF与△ABC的周长比是1:2
D.△DEF与△ABC的面积比是1:2
7.如图,已知△ABC和△EDC是以点C为位似中心的位似图形,且△ABC和△EDC的位似比为1:2,△ABC周长为2,则△EDC的周长是( )
A.2 B.4 C.6 D.8
8.如图,正方形OEFG和正方形ABCD是位似图形,且点F与点C是一对对应点,点F的坐标是(1,1),点C的坐标是(4,2);则它们的位似中心的坐标是( )
A.(0,0) B.(﹣1,0) C.(﹣2,0) D.(﹣3,0)
9.如图,在平面直角坐标系xOy中,正方形ABCD和正方形BEFG是以原点O为位似中心的位似图形,且相似比是,点A,B,E在x轴上,若正方形BEFG的边长为12,则点C的坐标为( )
A.(6,2) B.(6,4) C.(4,4) D.(8,4)
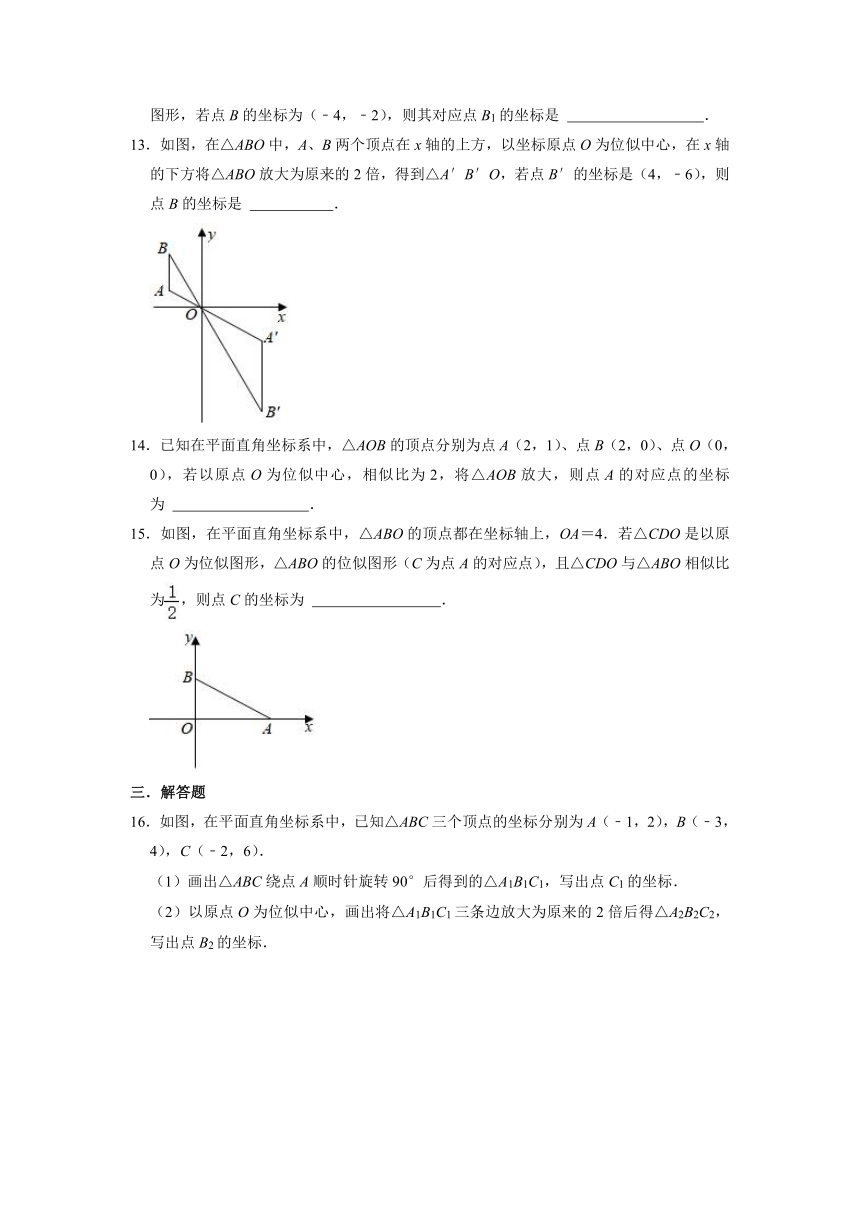
10.如图,已知矩形OABC与矩形ODEF是位似图形,M是位似中心,若点B的坐标为(﹣2,4),点E的坐标为(1,2),则点M的坐标为( )
A.(4,0) B.(﹣2,0) C.(3,0) D.(2,0)
二.填空题
11.如图,以点O为位似中心,将△OAB放大后得到△OCD,OA=2,OC=5,则= .
12.在平面直角坐标系中,△ABC与△A1B1C1的相似比是2:1,并且是关于原点O的位似图形,若点B的坐标为(﹣4,﹣2),则其对应点B1的坐标是 .
13.如图,在△ABO中,A、B两个顶点在x轴的上方,以坐标原点O为位似中心,在x轴的下方将△ABO放大为原来的2倍,得到△A′B′O,若点B′的坐标是(4,﹣6),则点B的坐标是 .
14.已知在平面直角坐标系中,△AOB的顶点分别为点A(2,1)、点B(2,0)、点O(0,0),若以原点O为位似中心,相似比为2,将△AOB放大,则点A的对应点的坐标为 .
15.如图,在平面直角坐标系中,△ABO的顶点都在坐标轴上,OA=4.若△CDO是以原点O为位似图形,△ABO的位似图形(C为点A的对应点),且△CDO与△ABO相似比为,则点C的坐标为 .
三.解答题
16.如图,在平面直角坐标系中,已知△ABC三个顶点的坐标分别为A(﹣1,2),B(﹣3,4),C(﹣2,6).
(1)画出△ABC绕点A顺时针旋转90°后得到的△A1B1C1,写出点C1的坐标.
(2)以原点O为位似中心,画出将△A1B1C1三条边放大为原来的2倍后得△A2B2C2,写出点B2的坐标.
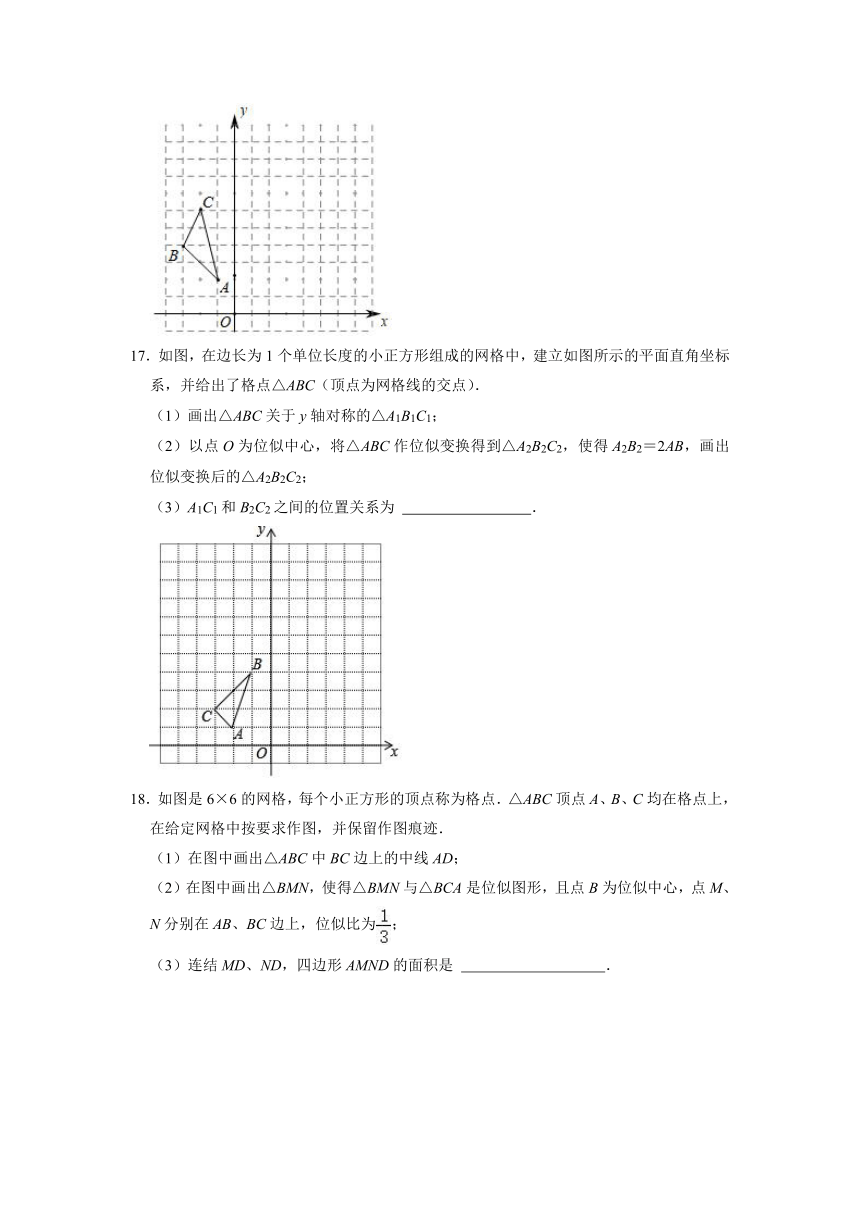
17.如图,在边长为1个单位长度的小正方形组成的网格中,建立如图所示的平面直角坐标系,并给出了格点△ABC(顶点为网格线的交点).
(1)画出△ABC关于y轴对称的△A1B1C1;
(2)以点O为位似中心,将△ABC作位似变换得到△A2B2C2,使得A2B2=2AB,画出位似变换后的△A2B2C2;
(3)A1C1和B2C2之间的位置关系为 .
18.如图是6×6的网格,每个小正方形的顶点称为格点.△ABC顶点A、B、C均在格点上,在给定网格中按要求作图,并保留作图痕迹.
(1)在图中画出△ABC中BC边上的中线AD;
(2)在图中画出△BMN,使得△BMN与△BCA是位似图形,且点B为位似中心,点M、N分别在AB、BC边上,位似比为;
(3)连结MD、ND,四边形AMND的面积是 .
参考答案
一.选择题
1.【解析】解:A、∵BC∥ED,
∴△ADE∽△ABC,且两个三角形对应点连线相交于一点,
∴两个三角形是位似图形,本选项说法正确,不符合题意;
B、点A是两个三角形的位似中心,本选项说法正确,不符合题意;
C、点B与点D、点C与点E是对应位似点,本选项说法正确,不符合题意;
D、AD:AB是相似比,故本选项说法不正确,符合题意;
故选:D.
2.【解析】解:连接OA、OB、OC,
∵图②的三个顶点分别在OA、OB、OC上,
∴以O为位似中心且与△ABC位似的图形序号是②,
故选:B.
3.【解析】解:∵△ABC与△A1B1C1位似,
∴△ABC∽△A1B1C1,AC∥A1C1,
∴△AOC∽△A1OC1,
∴==,
∴△ABC与△A1B1C1的周长比为1:2,
故选:A.
4.【解析】解:∵以原点O为位似中心,把线段AB缩短为原来的,点B的坐标为(﹣4,3),
∴点D的坐标为(﹣4×,3×)或[﹣4×(﹣),3×(﹣)].即(﹣1,)或(1,﹣).
故选:D.
5.【解析】解:∵△A'B'C'是△ABC以点O为位似中心经过位似变换得到的,
∴△A'B'C'∽△ABC,A'B'∥AB,
∴△OA'B'∽△OAB,
∴==,
∴=()2=,
故选:A.
6.【解析】解:∵AO、BO、CO的中点分别为D、E、F,
∴EF∥BC,EF=BC,DF∥AC,DF=AC,DE∥AB,DE=AB,
∴△DEF∽△ABC,
∴△DEF与△ABC是位似图形,位似中心为点O,
∴△DEF与△ABC是相似图形,
∴△DEF与△ABC的周长比是1:2,△DEF与△ABC的面积比是1:4,
∴D选项说法错误,
故选:D.
7.【解析】解:∵△ABC和△EDC是以点C为位似中心的位似图形,
∴△ABC∽△EDC,
∵△ABC和△EDC的位似比为1:2,
∴△ABC和△EDC的相似比为1:2,
则△ABC与△EDC的周长比为1:2,
∵△ABC周长为2,
∴△EDC的周长是:4.
故选:B.
8.【解析】解:∵点F与点C是一对对应点,可知两个位似图形在位似中心同旁,位似中心就是CF与x轴的交点,
设直线CF解析式为y=kx+b,
将C(4,2),F(1,1)代入,
得,
解得 ,
即y=x+,
令y=0得x=﹣2,
∴O′坐标是(﹣2,0);
故选:C.
9.【解析】解:∵正方形ABCD和正方形BEFG是以原点O为位似中心的位似图形,且相似比是,正方形BEFG的边长为12,
∴BC∥EF,=,BC=4,
∴△OBC∽△OEF,
∴==,即=,
解得,OB=6,
∴点C的坐标为(6,4),
故选:B.
10.【解析】解:∵四边形OABC、四边形ODEF为矩形,点B的坐标为(﹣2,4),点E的坐标为(1,2),
∴OC=4,EF=2,OF=1,
∵矩形OABC与矩形ODEF是位似图形,
∴EF∥OC,
∴=,即=,
解得,MO=2,
∴点M的坐标为(2,0),
故选:D.
二.填空题
11.【解析】解:∵以点O为位似中心,将△OAB放大后得到△OCD,OA=2,OC=5,
∴△BOA∽△DOC,
∴=,
∴=.
故答案为:.
12.【解析】解:∵△ABC与△A1B1C1的相似比是2:1,并且是关于原点O的位似图形,点B的坐标为(﹣4,﹣2),
∴其对应点B1的坐标是(﹣4×,﹣2×)或(﹣4×(﹣),﹣2×(﹣)),即(﹣2,﹣1)或(2,1),
故答案为:(﹣2,﹣1)或(2,1).
13.【解析】解:∵以坐标原点O为位似中心,在x轴的下方将△ABO放大为原来的2倍,得到△A′B′O,点B′的坐标是(4,﹣6),
∴点B的坐标是(4×(﹣),﹣6×(﹣)),即(﹣2,3),
故答案为:(﹣2,3).
14.【解析】解:如图,观察图象可知,点A的对应点的坐标为(4,2)或(﹣4,﹣2).
故答案为:(4,2)或(﹣4,﹣2).
15.【解析】解:∵OA=4,
∴A(4,0),
∵△CDO是以原点O为位似图形,△ABO的位似图形,且△CDO与△ABO相似比为,
∴C点坐标为(×4,0)或(﹣×4,0),即C(2,0)或(﹣2,0).
故答案为(2,0)或(﹣2,0).
三.解答题
16.【解析】解:(1)如图,△A1B1C1为所求作的三角形,C1(3,3).
(2)如图所示,则△A2B2C2为所求作的三角形,B2(2,8).
17.【解析】解:(1)如图,△A1B1C1即为所求.
(2)如图,△A2B2C2即为所求.
(3)A1C1∥B2C2或平行.
故答案为:A1C1∥B2C2或平行.
18.【解析】解:(1)如图,线段AD即为所求.
(2)如图,△BMN即为所求.
(3)S四边形AMND=S△ABC﹣S△BMN﹣S△ADC=×6×4﹣×3×4﹣×2×=.
故答案为:.
∵∠BAC=90°,AC=3,AB=4,
∴BC=5.
又∵ AF BC= AC AB,
∴,
∴.
∵AC=AD,AF⊥CD,
∴.
一.选择题
1.如图,BC∥ED,下列说法不正确的是( )
A.两个三角形是位似图形
B.点A是两个三角形的位似中心
C.点B与点D、点C与点E是对应位似点
D.AC:AB是相似比
2.在下列四个三角形中,以O为位似中心且与△ABC位似的图形序号是( )
A.① B.② C.③ D.④
3.如图,△ABC与△A1B1C1位似,位似中心是点O,若OA:OA1=1:2,则△ABC与△A1B1C1的周长比是( )
A.1:2 B.1:3 C.1:4 D.1:
4.已知点A(0,3),B(﹣4,3),以原点O为位似中心,把线段AB缩短为原来的,其中点C与点A对应,点D与点B对应.则点D的坐标为( )
A.(﹣1,) B.(1,﹣)
C.(,﹣1)或(﹣,1) D.(﹣1,)或(1,﹣)
5.如图,△A'B'C'是△ABC以点O为位似中心经过位似变换得到的,若AA':OA'=2:3,则△ABC的面积与△A'B'C'的面积比是( )
A.25:9 B.9:4 C.25:3 D.5:3
6.如图,在△ABC外任取一点O,连接AO、BO、CO,并分别取它们的中点D、E、F,顺次连接DE、EF、DF得到△DEF,则下列说法错误的是( )
A.△DEF与△ABC是位似图形
B.△DEF与△ABC是相似图形
C.△DEF与△ABC的周长比是1:2
D.△DEF与△ABC的面积比是1:2
7.如图,已知△ABC和△EDC是以点C为位似中心的位似图形,且△ABC和△EDC的位似比为1:2,△ABC周长为2,则△EDC的周长是( )
A.2 B.4 C.6 D.8
8.如图,正方形OEFG和正方形ABCD是位似图形,且点F与点C是一对对应点,点F的坐标是(1,1),点C的坐标是(4,2);则它们的位似中心的坐标是( )
A.(0,0) B.(﹣1,0) C.(﹣2,0) D.(﹣3,0)
9.如图,在平面直角坐标系xOy中,正方形ABCD和正方形BEFG是以原点O为位似中心的位似图形,且相似比是,点A,B,E在x轴上,若正方形BEFG的边长为12,则点C的坐标为( )
A.(6,2) B.(6,4) C.(4,4) D.(8,4)
10.如图,已知矩形OABC与矩形ODEF是位似图形,M是位似中心,若点B的坐标为(﹣2,4),点E的坐标为(1,2),则点M的坐标为( )
A.(4,0) B.(﹣2,0) C.(3,0) D.(2,0)
二.填空题
11.如图,以点O为位似中心,将△OAB放大后得到△OCD,OA=2,OC=5,则= .
12.在平面直角坐标系中,△ABC与△A1B1C1的相似比是2:1,并且是关于原点O的位似图形,若点B的坐标为(﹣4,﹣2),则其对应点B1的坐标是 .
13.如图,在△ABO中,A、B两个顶点在x轴的上方,以坐标原点O为位似中心,在x轴的下方将△ABO放大为原来的2倍,得到△A′B′O,若点B′的坐标是(4,﹣6),则点B的坐标是 .
14.已知在平面直角坐标系中,△AOB的顶点分别为点A(2,1)、点B(2,0)、点O(0,0),若以原点O为位似中心,相似比为2,将△AOB放大,则点A的对应点的坐标为 .
15.如图,在平面直角坐标系中,△ABO的顶点都在坐标轴上,OA=4.若△CDO是以原点O为位似图形,△ABO的位似图形(C为点A的对应点),且△CDO与△ABO相似比为,则点C的坐标为 .
三.解答题
16.如图,在平面直角坐标系中,已知△ABC三个顶点的坐标分别为A(﹣1,2),B(﹣3,4),C(﹣2,6).
(1)画出△ABC绕点A顺时针旋转90°后得到的△A1B1C1,写出点C1的坐标.
(2)以原点O为位似中心,画出将△A1B1C1三条边放大为原来的2倍后得△A2B2C2,写出点B2的坐标.
17.如图,在边长为1个单位长度的小正方形组成的网格中,建立如图所示的平面直角坐标系,并给出了格点△ABC(顶点为网格线的交点).
(1)画出△ABC关于y轴对称的△A1B1C1;
(2)以点O为位似中心,将△ABC作位似变换得到△A2B2C2,使得A2B2=2AB,画出位似变换后的△A2B2C2;
(3)A1C1和B2C2之间的位置关系为 .
18.如图是6×6的网格,每个小正方形的顶点称为格点.△ABC顶点A、B、C均在格点上,在给定网格中按要求作图,并保留作图痕迹.
(1)在图中画出△ABC中BC边上的中线AD;
(2)在图中画出△BMN,使得△BMN与△BCA是位似图形,且点B为位似中心,点M、N分别在AB、BC边上,位似比为;
(3)连结MD、ND,四边形AMND的面积是 .
参考答案
一.选择题
1.【解析】解:A、∵BC∥ED,
∴△ADE∽△ABC,且两个三角形对应点连线相交于一点,
∴两个三角形是位似图形,本选项说法正确,不符合题意;
B、点A是两个三角形的位似中心,本选项说法正确,不符合题意;
C、点B与点D、点C与点E是对应位似点,本选项说法正确,不符合题意;
D、AD:AB是相似比,故本选项说法不正确,符合题意;
故选:D.
2.【解析】解:连接OA、OB、OC,
∵图②的三个顶点分别在OA、OB、OC上,
∴以O为位似中心且与△ABC位似的图形序号是②,
故选:B.
3.【解析】解:∵△ABC与△A1B1C1位似,
∴△ABC∽△A1B1C1,AC∥A1C1,
∴△AOC∽△A1OC1,
∴==,
∴△ABC与△A1B1C1的周长比为1:2,
故选:A.
4.【解析】解:∵以原点O为位似中心,把线段AB缩短为原来的,点B的坐标为(﹣4,3),
∴点D的坐标为(﹣4×,3×)或[﹣4×(﹣),3×(﹣)].即(﹣1,)或(1,﹣).
故选:D.
5.【解析】解:∵△A'B'C'是△ABC以点O为位似中心经过位似变换得到的,
∴△A'B'C'∽△ABC,A'B'∥AB,
∴△OA'B'∽△OAB,
∴==,
∴=()2=,
故选:A.
6.【解析】解:∵AO、BO、CO的中点分别为D、E、F,
∴EF∥BC,EF=BC,DF∥AC,DF=AC,DE∥AB,DE=AB,
∴△DEF∽△ABC,
∴△DEF与△ABC是位似图形,位似中心为点O,
∴△DEF与△ABC是相似图形,
∴△DEF与△ABC的周长比是1:2,△DEF与△ABC的面积比是1:4,
∴D选项说法错误,
故选:D.
7.【解析】解:∵△ABC和△EDC是以点C为位似中心的位似图形,
∴△ABC∽△EDC,
∵△ABC和△EDC的位似比为1:2,
∴△ABC和△EDC的相似比为1:2,
则△ABC与△EDC的周长比为1:2,
∵△ABC周长为2,
∴△EDC的周长是:4.
故选:B.
8.【解析】解:∵点F与点C是一对对应点,可知两个位似图形在位似中心同旁,位似中心就是CF与x轴的交点,
设直线CF解析式为y=kx+b,
将C(4,2),F(1,1)代入,
得,
解得 ,
即y=x+,
令y=0得x=﹣2,
∴O′坐标是(﹣2,0);
故选:C.
9.【解析】解:∵正方形ABCD和正方形BEFG是以原点O为位似中心的位似图形,且相似比是,正方形BEFG的边长为12,
∴BC∥EF,=,BC=4,
∴△OBC∽△OEF,
∴==,即=,
解得,OB=6,
∴点C的坐标为(6,4),
故选:B.
10.【解析】解:∵四边形OABC、四边形ODEF为矩形,点B的坐标为(﹣2,4),点E的坐标为(1,2),
∴OC=4,EF=2,OF=1,
∵矩形OABC与矩形ODEF是位似图形,
∴EF∥OC,
∴=,即=,
解得,MO=2,
∴点M的坐标为(2,0),
故选:D.
二.填空题
11.【解析】解:∵以点O为位似中心,将△OAB放大后得到△OCD,OA=2,OC=5,
∴△BOA∽△DOC,
∴=,
∴=.
故答案为:.
12.【解析】解:∵△ABC与△A1B1C1的相似比是2:1,并且是关于原点O的位似图形,点B的坐标为(﹣4,﹣2),
∴其对应点B1的坐标是(﹣4×,﹣2×)或(﹣4×(﹣),﹣2×(﹣)),即(﹣2,﹣1)或(2,1),
故答案为:(﹣2,﹣1)或(2,1).
13.【解析】解:∵以坐标原点O为位似中心,在x轴的下方将△ABO放大为原来的2倍,得到△A′B′O,点B′的坐标是(4,﹣6),
∴点B的坐标是(4×(﹣),﹣6×(﹣)),即(﹣2,3),
故答案为:(﹣2,3).
14.【解析】解:如图,观察图象可知,点A的对应点的坐标为(4,2)或(﹣4,﹣2).
故答案为:(4,2)或(﹣4,﹣2).
15.【解析】解:∵OA=4,
∴A(4,0),
∵△CDO是以原点O为位似图形,△ABO的位似图形,且△CDO与△ABO相似比为,
∴C点坐标为(×4,0)或(﹣×4,0),即C(2,0)或(﹣2,0).
故答案为(2,0)或(﹣2,0).
三.解答题
16.【解析】解:(1)如图,△A1B1C1为所求作的三角形,C1(3,3).
(2)如图所示,则△A2B2C2为所求作的三角形,B2(2,8).
17.【解析】解:(1)如图,△A1B1C1即为所求.
(2)如图,△A2B2C2即为所求.
(3)A1C1∥B2C2或平行.
故答案为:A1C1∥B2C2或平行.
18.【解析】解:(1)如图,线段AD即为所求.
(2)如图,△BMN即为所求.
(3)S四边形AMND=S△ABC﹣S△BMN﹣S△ADC=×6×4﹣×3×4﹣×2×=.
故答案为:.
∵∠BAC=90°,AC=3,AB=4,
∴BC=5.
又∵ AF BC= AC AB,
∴,
∴.
∵AC=AD,AF⊥CD,
∴.
同课章节目录
- 第一章 特殊平行四边形
- 1 菱形的性质与判定
- 2 矩形的性质与判定
- 3 正方形的性质与判定
- 第二章 一元二次方程
- 1 认识一元二次方程
- 2 用配方法求解一元二次方程
- 3 用公式法求解一元二次方程
- 4 用因式分解法求解一元二次方程
- 5 一元二次方程的根与系数的关系
- 6 应用一元二次方程
- 第三章 概率的进一步认识
- 1 用树状图或表格求概率
- 2 用频率估计概率
- 第四章 图形的相似
- 1 成比例线段
- 2 平行线分线段成比例
- 3 相似多边形
- 4 探索三角形相似的条件
- 5 相似三角形判定定理的证明
- 6 利用相似三角形测高
- 7 相似三角形的性质
- 8 图形的位似
- 第五章 投影与视图
- 1 投影
- 2 视图
- 第六章 反比例函数
- 1 反比例函数
- 2 反比例函数的图象与性质
- 3 反比例函数的应用
