第 1 章 集合与逻辑 章节复习练习卷 -2021-2022学年高一上学期数学沪教版(2020)必修第一册(Word含答案解析)
文档属性
| 名称 | 第 1 章 集合与逻辑 章节复习练习卷 -2021-2022学年高一上学期数学沪教版(2020)必修第一册(Word含答案解析) |  | |
| 格式 | doc | ||
| 文件大小 | 981.2KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 上教版(2020) | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-10-19 21:45:23 | ||
图片预览




文档简介
高一数学《第 1 章 集合与逻辑》章节复习练习卷【5】
一、填空题(共10小题,每小题4分,满分40分)
1、已知集合A={x|x2-2x-3≤0,x∈N },B={1,3},定义集合A,B之间的运算“*”:A*B={x|x=x1+x2,x1∈A,x2∈B},则A*B中的所有元素数字之和为( )
A.15 B.16 C.20 D.21
2、定义一种新的集合运算※:A※B={x|x∈A且x B}.若集合A={x|x2-4x+3<0},B={x|2≤x≤4},则按运算※,B※A等于
3、《西游记》《三国演义》《水浒传》和《红楼梦》是中国古典文学瑰宝,并称为中国古典小说四大名著.某中学为了了解本校学生阅读四大名著的情况,随机调查了100位学生,其中阅读过《西游记》或《红楼梦》的学生共有90位,阅读过《红楼梦》的学生共有80位,阅读过《西游记》且阅读过《红楼梦》的学生共有60位,则该校阅读过《西游记》的学生人数与该校学生总数比值的估计值为
4、某校高三(1)班有50名学生,春季运动会上,有15名学生参加了田赛项目,有20名学生参加了径赛项目,已知田赛和径赛都参加的有8名同学,则该班学生中田赛和径赛都没有参加的人数为
5、伟人毛泽东的《清平乐 六盘山》传颂至今,“天高云淡,望断南飞雁.不到长城非好汉,屈指行程二万,六盘山上高峰,红旗漫卷西风,今日长缨在手,何时缚住苍龙?”现在许多人前往长城游玩时,经常会用“不到长城非好汉”来勉励自己,由此推断,“到长城”是“为好汉”的 (选“充分条件”; “必要条件”; “充要条件”; “既不充分也不必要条件”之一填空)
6、《墨子·经说上》上说:“小故,有之不必然,无之必不然,体也,若有端,大故,有之必然,若见之成见也.”这一段文字蕴含着十分丰富的逻辑思想,那么文中的“小故”指的是逻辑中的___________(选“充分条件”; “必要条件”; “充要条件”; “既不充分也不必要条件”之一填空)
7、右图为由电池、开关和灯泡组成的电路,假定所有零件均能正常工作,
则电路中“开关K1和K2有且只有一个闭合”是“灯泡L亮”
的 条件;
(填“充分不必要”;“必要不充分”;“充要”;“既不充分也不必要” 之一填空)
8、王安石在《游褒禅山记》中写道:“世之奇伟、瑰怪,非常之观,常在险远,而人之所罕至焉,故非有志者不能至也.”请问“有志”是能到达“奇伟、瑰怪,非常之观”的______条件.(填“充分”“必要”“充要”中的一个)
9、某校有17名学生,每人至少参加全国数学 物理 化学三科竞赛中的一科,已知其中参加数学竞赛的有11人,参加物理竞赛的有7人,参加化学竞赛的有9人,同时参加数学和物理竞赛的有4人,同时参加数学和化学竞赛的有5人,同时参加物理和化学竞赛的有3人,则三科竞赛都参加的有___________人.
10、对于平面上的点集,如果连接中任意两点的线段必定包含于,则称为平面上的凸集,给出平面上4个点集的图形如下(阴影区域及其边界):
其中为凸集的是 (写出所有凸集相应图形的序号)。
二、选择题(共4小题 每小题4分,满分16分)
11、在集合上定义两种运算和如下
那么( )
A. B. C. D.
12、某校为调查学生参加研究性学习的情况,从全校学生中随机抽取名学生,其中参加“数学类”的有名,既参加“数学类”又参加“理化类”的有名,“数学类”和“理化类”都没有参加的有名,则该校参加“理化类”研究性学习的学生人数与该校学生总数的比值的估计值是( )
A. B. C. D.
13、调查了100名携带药品出国的旅游者,其中75人带有感冒药,80人带有胃药,那么对于既带感冒药又带胃药的人数统计中,下列说法正确的是( )
A.最多人数是55 B.最少人数是55 C.最少人数是75 D.最多人数是80
14、设计如下图的四个电路图,则能表示“开关A闭合”是“灯泡B亮”的必要不充分条件的一个电路图是( )
A. B. C. D.
三、解答题(共4小题,满分44分;请在答题卡指定区域内作答,解答时应写出文字说明、证明过程或演算步骤)
15.(本题8分)
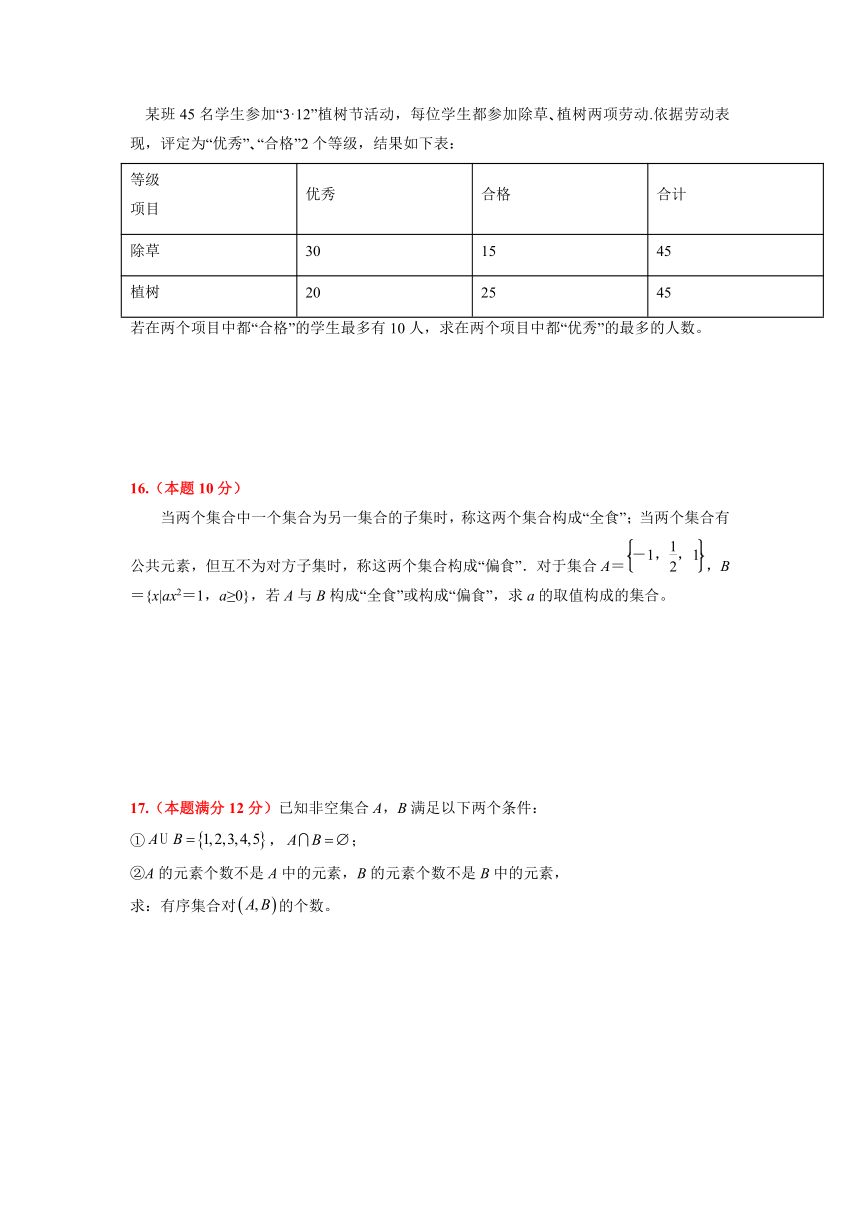
某班45名学生参加“3·12”植树节活动,每位学生都参加除草 植树两项劳动.依据劳动表现,评定为“优秀” “合格”2个等级,结果如下表:
等级项目 优秀 合格 合计
除草 30 15 45
植树 20 25 45
若在两个项目中都“合格”的学生最多有10人,求在两个项目中都“优秀”的最多的人数。
16.(本题10分)
当两个集合中一个集合为另一集合的子集时,称这两个集合构成“全食”;当两个集合有公共元素,但互不为对方子集时,称这两个集合构成“偏食”.对于集合A=,B={x|ax2=1,a≥0},若A与B构成“全食”或构成“偏食”,求a的取值构成的集合。
17.(本题满分12分)已知非空集合A,B满足以下两个条件:
①,;
②A的元素个数不是A中的元素,B的元素个数不是B中的元素,
求:有序集合对的个数。
18.(本题满分14分、第1小题满分6分、第2小题满分8分)
在①、②、③这三个条件中任选一个,补充在下面横线上,求解下列问题:
设集合___________,集合,
(1)定义且,当时,求;
(2)若,求实数的取值范围.
注:如果选择多个条件分别解答,按第一个解答计分.
【教师版】高一数学《第 1 章 集合与逻辑》章节复习练习卷【5】
一、填空题(共10小题,每小题4分,满分40分)
1、已知集合A={x|x2-2x-3≤0,x∈N },B={1,3},定义集合A,B之间的运算“*”:A*B={x|x=x1+x2,x1∈A,x2∈B},则A*B中的所有元素数字之和为( )
A.15 B.16 C.20 D.21
【答案】D;
【解析】由x2-2x-3≤0,得(x+1)(x-3)≤0,得A={0,1,2,3}.因为A*B={x|x=x1+x2,x1∈A,x2∈B},所以A*B中的元素有:0+1=1,0+3=3,1+1=2,1+3=4,2+1=3(舍去),2+3=5,3+1=4(舍去),3+3=6,所以A*B={1,2,3,4,5,6},所以A*B中的所有元素数字之和为21;
【说明】注意即时理解新定义、新运算解之;
2、定义一种新的集合运算※:A※B={x|x∈A且x B}.若集合A={x|x2-4x+3<0},B={x|2≤x≤4},则按运算※,B※A等于
【答案】{x|3≤x≤4}
【解析】由题意知,A={x|1【说明】注意即时理解新定义与解不等式进行简单交汇;
3、《西游记》《三国演义》《水浒传》和《红楼梦》是中国古典文学瑰宝,并称为中国古典小说四大名著.某中学为了了解本校学生阅读四大名著的情况,随机调查了100位学生,其中阅读过《西游记》或《红楼梦》的学生共有90位,阅读过《红楼梦》的学生共有80位,阅读过《西游记》且阅读过《红楼梦》的学生共有60位,则该校阅读过《西游记》的学生人数与该校学生总数比值的估计值为
【答案】0.7(2019全国卷3改编)
【解析】根据题意阅读过《红楼梦》《西游记》的人数用Venn图表示如图,所以该校阅读过《西游记》的学生人数与该校学生总数比值的估计值为=0.7;
【说明】注意用好文氏图,直观形象;
4、某校高三(1)班有50名学生,春季运动会上,有15名学生参加了田赛项目,有20名学生参加了径赛项目,已知田赛和径赛都参加的有8名同学,则该班学生中田赛和径赛都没有参加的人数为
【答案】23
【解析】设高三(1)班有50名学生组成的集合为 ,参加田赛项目的学生组成的集合为,参加径赛项目的学生组成的集合为由题意集合有15个元素,有20个元素,中有8个元素
所以有个元素.所以该班学生中田赛和径赛都没有参加的人数为;
【说明】可以尝试用文氏图,直观形象;
5、伟人毛泽东的《清平乐 六盘山》传颂至今,“天高云淡,望断南飞雁.不到长城非好汉,屈指行程二万,六盘山上高峰,红旗漫卷西风,今日长缨在手,何时缚住苍龙?”现在许多人前往长城游玩时,经常会用“不到长城非好汉”来勉励自己,由此推断,“到长城”是“为好汉”的 (选“充分条件”; “必要条件”; “充要条件”; “既不充分也不必要条件”之一填空)
【答案】必要条件
【名师解析】设为不到长城,推出非好汉,即,则,即好汉到长城,
故“到长城”是“好汉”的必要条件,故选:.
6、《墨子·经说上》上说:“小故,有之不必然,无之必不然,体也,若有端,大故,有之必然,若见之成见也.”这一段文字蕴含着十分丰富的逻辑思想,那么文中的“小故”指的是逻辑中的___________(选“充分条件”; “必要条件”; “充要条件”; “既不充分也不必要条件”之一填空)
【答案】必要条件
【解析】由“小故,有之不必然,无之必不然也”,知“小故”是导致某个结果出现的几个条件中的一个或一部分条件,故“小故”指的是逻辑中的必要条件;
7、右图为由电池、开关和灯泡组成的电路,假定所有零件均能正常工作,
则电路中“开关K1和K2有且只有一个闭合”是“灯泡L亮”
的 条件;
(填“充分不必要”;“必要不充分”;“充要”;“既不充分也不必要” 之一填空)
【答案】充分不必要;
【解析】当开关K1和K2有且只有一个闭合时,灯泡L亮
当灯泡L亮时,开关K1和K2有可能都闭合
即电路中“开关K1和K2有且只有一个闭合”是“灯泡L亮”的充分不必要条件
故答案为:充分不必要
8、王安石在《游褒禅山记》中写道:“世之奇伟、瑰怪,非常之观,常在险远,而人之所罕至焉,故非有志者不能至也.”请问“有志”是能到达“奇伟、瑰怪,非常之观”的______条件.(填“充分”“必要”“充要”中的一个)
【答案】必要
【名师解析】因为“非有志者不能至”所以“能至是有志者”,因此“有志”是能到达“奇伟、瑰怪,非常之观”的必要条件.故答案为:必要
9、某校有17名学生,每人至少参加全国数学 物理 化学三科竞赛中的一科,已知其中参加数学竞赛的有11人,参加物理竞赛的有7人,参加化学竞赛的有9人,同时参加数学和物理竞赛的有4人,同时参加数学和化学竞赛的有5人,同时参加物理和化学竞赛的有3人,则三科竞赛都参加的有___________人.
【提示】设参加数学、物理、化学竞赛的学生组成集合、、,根据已知条件结合集合间的运算即可求解;
【答案】
【解析】
设参加数学竞赛的学生组成集合,参加物理竞赛的学生组成集合,参加化学竞赛的学生组成集合,
根据题意可得:,,,,
,,,
因为
所以
解得:,
所以三科竞赛都参加的有人,
故答案为:
【说明】注意用好文氏图,直观形象;
10、对于平面上的点集,如果连接中任意两点的线段必定包含于,则称为平面上的凸集,给出平面上4个点集的图形如下(阴影区域及其边界):
其中为凸集的是 (写出所有凸集相应图形的序号)。
【答案】②③;
【解析】根据题意,在①④中适当选取两点,连接起来,不符合题意。
【说明】只要透彻理解题中“凸集”的含义,就能很快找出正确答案;
二、选择题(共4小题 每小题4分,满分16分)
11、在集合上定义两种运算和如下
那么( )
A. B. C. D.
【答案】A;
【解析】由上表可知:,故,选A;
【说明】认真看懂上面两个表格,弄清两种运算和,解答本题其实一点都不难。
12、某校为调查学生参加研究性学习的情况,从全校学生中随机抽取名学生,其中参加“数学类”的有名,既参加“数学类”又参加“理化类”的有名,“数学类”和“理化类”都没有参加的有名,则该校参加“理化类”研究性学习的学生人数与该校学生总数的比值的估计值是( )
A. B. C. D.
【答案】C
【解析】设参加“数学类”的学生人数构成集合,参加“理化类”的学生人数构成集合,其中只参加“理化类”的学生人数为人,样本100人构成全集,
根据题意,可得,解得,
所以参加“理化类”的学生人数为人,
所以参加“理化类”研究性学习的学生人数与该校学生总数的比值的估计值是.
故选:C.
13、调查了100名携带药品出国的旅游者,其中75人带有感冒药,80人带有胃药,那么对于既带感冒药又带胃药的人数统计中,下列说法正确的是( )
A.最多人数是55 B.最少人数是55 C.最少人数是75 D.最多人数是80
【答案】B
【解析】设100名携带药品出国的旅游者组成全集I,其中带感冒药的人组成集合A,带胃药的人组成集合B.
又设所携带药品既非感冒药又非胃药的人数为x,则x∈[0,20],以上两种药都带的人数为y.
根据题意列出Venn图,如图所示,由图可知,x+75+80-y=100.
所以,y=55+x.,又因为 0≤x≤20,所以,55≤y≤75,故最少人数是55.故选B;
14、设计如下图的四个电路图,则能表示“开关A闭合”是“灯泡B亮”的必要不充分条件的一个电路图是( )
A. B. C. D.
【提示】根据“开关A闭合”是“灯泡B亮”的必要不充分条件判断出:开关A闭合推不出灯泡B亮,但灯泡B亮能推出开关A闭合,从而选出选项.
【答案】C;
【解析】选项A:“开关A闭合”是“灯泡B亮”的充分不必要条件;
选项B:“开关A闭合”是“灯泡B亮”的充要条件;
选项C:“开关A闭合”是“灯泡B亮”的必要不充分条件;
选项D:“开关A闭合”是“灯泡B亮”的既不充分也不必要条件.
故选:C.
三、解答题(共4小题,满分44分;请在答题卡指定区域内作答,解答时应写出文字说明、证明过程或演算步骤)
15.(本题8分)
某班45名学生参加“3·12”植树节活动,每位学生都参加除草 植树两项劳动.依据劳动表现,评定为“优秀” “合格”2个等级,结果如下表:
等级项目 优秀 合格 合计
除草 30 15 45
植树 20 25 45
若在两个项目中都“合格”的学生最多有10人,求在两个项目中都“优秀”的最多的人数。
【提示】用集合表示除草优秀的学生,表示椿树优秀的学生,全班学生用全集表示,则表示除草合格的学生,则表示植树合格的学生,作出Venn图,易得它们的关系,从而得出结论;
【答案】15;
【解析】用集合表示除草优秀的学生,表示椿树优秀的学生,全班学生用全集表示,则表示除草合格的学生,则表示植树合格的学生,作出Venn图,如图,
设两个项目都优秀的人数为,两个项目都是合格的人数为,由图可得,,因为,所以;
【说明】集合与逻辑问题中 遇到涉及集合运算与元素个数问题,文氏图可以直观地帮助分析、列式与结合限制条件解之。
16.(本题10分)
当两个集合中一个集合为另一集合的子集时,称这两个集合构成“全食”;当两个集合有公共元素,但互不为对方子集时,称这两个集合构成“偏食”.对于集合A=,B={x|ax2=1,a≥0},若A与B构成“全食”或构成“偏食”,求a的取值构成的集合。
【答案】{0,1,4}
【解析】因为,B={x|ax2=1,a≥0},
所以,当a=0时,B为空集,此时满足B A,
所以,集合A与B构成“全食”;
若a>0,则B=.由题意知=1或=,
当=1时,B={1,-1},B A,A与B构成“全食”;
当=时,B=,A与B构成“偏食”.
解得a=1或a=4.综上,a的取值集合为{0,1,4}.
17.(本题满分12分)已知非空集合A,B满足以下两个条件:
①,;
②A的元素个数不是A中的元素,B的元素个数不是B中的元素,
求:有序集合对的个数。
【答案】8;
【解析】由题意,符合要求的情况分为以下几类:
(1)当集合A只有一个元素时,集合B中有四个元素,且,
故,,共计1种;
(2)当集合A有两个元素时,集合B中有三个元素,且,
故可能结果为:①,;②,;
③,,共计3种;
(3)当集合A有三个元素时,集合B中有两个元素,且,
故可能结果为:①,;②,;
③,,共计3种;
(4)当集合A中有4个元素时,集合B中有1个元素,且,
故,,共计1种.
所以有序集合对的个数为.
18.(本题满分14分、第1小题满分6分、第2小题满分8分)
在①、②、③这三个条件中任选一个,补充在下面横线上,求解下列问题:
设集合___________,集合,
(1)定义且,当时,求;
(2)若,求实数的取值范围.
注:如果选择多个条件分别解答,按第一个解答计分.
【答案】(1);(2).
【解析】
选①:
(1),若,则,即,解得,
若,,无解,
则的解集为,,
,即,解得,,
则.
(2)因为,所以,即,,
因为,所以,解得,的取值范围为.
选②:
(1),解得,,
,即,解得,,
则.
(2)因为,所以,即,,
因为,所以,解得,的取值范围为.
选③:
(1),,解得,,
,即,解得,,
则.
(2)因为,所以,即,,
因为,所以,解得,的取值范围为.
【说明】本题属于“集合中的结构不良问题”;综合考查学生的命题构成与结合教材概念、公式与推导思路、过程进行推导、论证的能力;
①
②
③
④
①
②
③
④
一、填空题(共10小题,每小题4分,满分40分)
1、已知集合A={x|x2-2x-3≤0,x∈N },B={1,3},定义集合A,B之间的运算“*”:A*B={x|x=x1+x2,x1∈A,x2∈B},则A*B中的所有元素数字之和为( )
A.15 B.16 C.20 D.21
2、定义一种新的集合运算※:A※B={x|x∈A且x B}.若集合A={x|x2-4x+3<0},B={x|2≤x≤4},则按运算※,B※A等于
3、《西游记》《三国演义》《水浒传》和《红楼梦》是中国古典文学瑰宝,并称为中国古典小说四大名著.某中学为了了解本校学生阅读四大名著的情况,随机调查了100位学生,其中阅读过《西游记》或《红楼梦》的学生共有90位,阅读过《红楼梦》的学生共有80位,阅读过《西游记》且阅读过《红楼梦》的学生共有60位,则该校阅读过《西游记》的学生人数与该校学生总数比值的估计值为
4、某校高三(1)班有50名学生,春季运动会上,有15名学生参加了田赛项目,有20名学生参加了径赛项目,已知田赛和径赛都参加的有8名同学,则该班学生中田赛和径赛都没有参加的人数为
5、伟人毛泽东的《清平乐 六盘山》传颂至今,“天高云淡,望断南飞雁.不到长城非好汉,屈指行程二万,六盘山上高峰,红旗漫卷西风,今日长缨在手,何时缚住苍龙?”现在许多人前往长城游玩时,经常会用“不到长城非好汉”来勉励自己,由此推断,“到长城”是“为好汉”的 (选“充分条件”; “必要条件”; “充要条件”; “既不充分也不必要条件”之一填空)
6、《墨子·经说上》上说:“小故,有之不必然,无之必不然,体也,若有端,大故,有之必然,若见之成见也.”这一段文字蕴含着十分丰富的逻辑思想,那么文中的“小故”指的是逻辑中的___________(选“充分条件”; “必要条件”; “充要条件”; “既不充分也不必要条件”之一填空)
7、右图为由电池、开关和灯泡组成的电路,假定所有零件均能正常工作,
则电路中“开关K1和K2有且只有一个闭合”是“灯泡L亮”
的 条件;
(填“充分不必要”;“必要不充分”;“充要”;“既不充分也不必要” 之一填空)
8、王安石在《游褒禅山记》中写道:“世之奇伟、瑰怪,非常之观,常在险远,而人之所罕至焉,故非有志者不能至也.”请问“有志”是能到达“奇伟、瑰怪,非常之观”的______条件.(填“充分”“必要”“充要”中的一个)
9、某校有17名学生,每人至少参加全国数学 物理 化学三科竞赛中的一科,已知其中参加数学竞赛的有11人,参加物理竞赛的有7人,参加化学竞赛的有9人,同时参加数学和物理竞赛的有4人,同时参加数学和化学竞赛的有5人,同时参加物理和化学竞赛的有3人,则三科竞赛都参加的有___________人.
10、对于平面上的点集,如果连接中任意两点的线段必定包含于,则称为平面上的凸集,给出平面上4个点集的图形如下(阴影区域及其边界):
其中为凸集的是 (写出所有凸集相应图形的序号)。
二、选择题(共4小题 每小题4分,满分16分)
11、在集合上定义两种运算和如下
那么( )
A. B. C. D.
12、某校为调查学生参加研究性学习的情况,从全校学生中随机抽取名学生,其中参加“数学类”的有名,既参加“数学类”又参加“理化类”的有名,“数学类”和“理化类”都没有参加的有名,则该校参加“理化类”研究性学习的学生人数与该校学生总数的比值的估计值是( )
A. B. C. D.
13、调查了100名携带药品出国的旅游者,其中75人带有感冒药,80人带有胃药,那么对于既带感冒药又带胃药的人数统计中,下列说法正确的是( )
A.最多人数是55 B.最少人数是55 C.最少人数是75 D.最多人数是80
14、设计如下图的四个电路图,则能表示“开关A闭合”是“灯泡B亮”的必要不充分条件的一个电路图是( )
A. B. C. D.
三、解答题(共4小题,满分44分;请在答题卡指定区域内作答,解答时应写出文字说明、证明过程或演算步骤)
15.(本题8分)
某班45名学生参加“3·12”植树节活动,每位学生都参加除草 植树两项劳动.依据劳动表现,评定为“优秀” “合格”2个等级,结果如下表:
等级项目 优秀 合格 合计
除草 30 15 45
植树 20 25 45
若在两个项目中都“合格”的学生最多有10人,求在两个项目中都“优秀”的最多的人数。
16.(本题10分)
当两个集合中一个集合为另一集合的子集时,称这两个集合构成“全食”;当两个集合有公共元素,但互不为对方子集时,称这两个集合构成“偏食”.对于集合A=,B={x|ax2=1,a≥0},若A与B构成“全食”或构成“偏食”,求a的取值构成的集合。
17.(本题满分12分)已知非空集合A,B满足以下两个条件:
①,;
②A的元素个数不是A中的元素,B的元素个数不是B中的元素,
求:有序集合对的个数。
18.(本题满分14分、第1小题满分6分、第2小题满分8分)
在①、②、③这三个条件中任选一个,补充在下面横线上,求解下列问题:
设集合___________,集合,
(1)定义且,当时,求;
(2)若,求实数的取值范围.
注:如果选择多个条件分别解答,按第一个解答计分.
【教师版】高一数学《第 1 章 集合与逻辑》章节复习练习卷【5】
一、填空题(共10小题,每小题4分,满分40分)
1、已知集合A={x|x2-2x-3≤0,x∈N },B={1,3},定义集合A,B之间的运算“*”:A*B={x|x=x1+x2,x1∈A,x2∈B},则A*B中的所有元素数字之和为( )
A.15 B.16 C.20 D.21
【答案】D;
【解析】由x2-2x-3≤0,得(x+1)(x-3)≤0,得A={0,1,2,3}.因为A*B={x|x=x1+x2,x1∈A,x2∈B},所以A*B中的元素有:0+1=1,0+3=3,1+1=2,1+3=4,2+1=3(舍去),2+3=5,3+1=4(舍去),3+3=6,所以A*B={1,2,3,4,5,6},所以A*B中的所有元素数字之和为21;
【说明】注意即时理解新定义、新运算解之;
2、定义一种新的集合运算※:A※B={x|x∈A且x B}.若集合A={x|x2-4x+3<0},B={x|2≤x≤4},则按运算※,B※A等于
【答案】{x|3≤x≤4}
【解析】由题意知,A={x|1
3、《西游记》《三国演义》《水浒传》和《红楼梦》是中国古典文学瑰宝,并称为中国古典小说四大名著.某中学为了了解本校学生阅读四大名著的情况,随机调查了100位学生,其中阅读过《西游记》或《红楼梦》的学生共有90位,阅读过《红楼梦》的学生共有80位,阅读过《西游记》且阅读过《红楼梦》的学生共有60位,则该校阅读过《西游记》的学生人数与该校学生总数比值的估计值为
【答案】0.7(2019全国卷3改编)
【解析】根据题意阅读过《红楼梦》《西游记》的人数用Venn图表示如图,所以该校阅读过《西游记》的学生人数与该校学生总数比值的估计值为=0.7;
【说明】注意用好文氏图,直观形象;
4、某校高三(1)班有50名学生,春季运动会上,有15名学生参加了田赛项目,有20名学生参加了径赛项目,已知田赛和径赛都参加的有8名同学,则该班学生中田赛和径赛都没有参加的人数为
【答案】23
【解析】设高三(1)班有50名学生组成的集合为 ,参加田赛项目的学生组成的集合为,参加径赛项目的学生组成的集合为由题意集合有15个元素,有20个元素,中有8个元素
所以有个元素.所以该班学生中田赛和径赛都没有参加的人数为;
【说明】可以尝试用文氏图,直观形象;
5、伟人毛泽东的《清平乐 六盘山》传颂至今,“天高云淡,望断南飞雁.不到长城非好汉,屈指行程二万,六盘山上高峰,红旗漫卷西风,今日长缨在手,何时缚住苍龙?”现在许多人前往长城游玩时,经常会用“不到长城非好汉”来勉励自己,由此推断,“到长城”是“为好汉”的 (选“充分条件”; “必要条件”; “充要条件”; “既不充分也不必要条件”之一填空)
【答案】必要条件
【名师解析】设为不到长城,推出非好汉,即,则,即好汉到长城,
故“到长城”是“好汉”的必要条件,故选:.
6、《墨子·经说上》上说:“小故,有之不必然,无之必不然,体也,若有端,大故,有之必然,若见之成见也.”这一段文字蕴含着十分丰富的逻辑思想,那么文中的“小故”指的是逻辑中的___________(选“充分条件”; “必要条件”; “充要条件”; “既不充分也不必要条件”之一填空)
【答案】必要条件
【解析】由“小故,有之不必然,无之必不然也”,知“小故”是导致某个结果出现的几个条件中的一个或一部分条件,故“小故”指的是逻辑中的必要条件;
7、右图为由电池、开关和灯泡组成的电路,假定所有零件均能正常工作,
则电路中“开关K1和K2有且只有一个闭合”是“灯泡L亮”
的 条件;
(填“充分不必要”;“必要不充分”;“充要”;“既不充分也不必要” 之一填空)
【答案】充分不必要;
【解析】当开关K1和K2有且只有一个闭合时,灯泡L亮
当灯泡L亮时,开关K1和K2有可能都闭合
即电路中“开关K1和K2有且只有一个闭合”是“灯泡L亮”的充分不必要条件
故答案为:充分不必要
8、王安石在《游褒禅山记》中写道:“世之奇伟、瑰怪,非常之观,常在险远,而人之所罕至焉,故非有志者不能至也.”请问“有志”是能到达“奇伟、瑰怪,非常之观”的______条件.(填“充分”“必要”“充要”中的一个)
【答案】必要
【名师解析】因为“非有志者不能至”所以“能至是有志者”,因此“有志”是能到达“奇伟、瑰怪,非常之观”的必要条件.故答案为:必要
9、某校有17名学生,每人至少参加全国数学 物理 化学三科竞赛中的一科,已知其中参加数学竞赛的有11人,参加物理竞赛的有7人,参加化学竞赛的有9人,同时参加数学和物理竞赛的有4人,同时参加数学和化学竞赛的有5人,同时参加物理和化学竞赛的有3人,则三科竞赛都参加的有___________人.
【提示】设参加数学、物理、化学竞赛的学生组成集合、、,根据已知条件结合集合间的运算即可求解;
【答案】
【解析】
设参加数学竞赛的学生组成集合,参加物理竞赛的学生组成集合,参加化学竞赛的学生组成集合,
根据题意可得:,,,,
,,,
因为
所以
解得:,
所以三科竞赛都参加的有人,
故答案为:
【说明】注意用好文氏图,直观形象;
10、对于平面上的点集,如果连接中任意两点的线段必定包含于,则称为平面上的凸集,给出平面上4个点集的图形如下(阴影区域及其边界):
其中为凸集的是 (写出所有凸集相应图形的序号)。
【答案】②③;
【解析】根据题意,在①④中适当选取两点,连接起来,不符合题意。
【说明】只要透彻理解题中“凸集”的含义,就能很快找出正确答案;
二、选择题(共4小题 每小题4分,满分16分)
11、在集合上定义两种运算和如下
那么( )
A. B. C. D.
【答案】A;
【解析】由上表可知:,故,选A;
【说明】认真看懂上面两个表格,弄清两种运算和,解答本题其实一点都不难。
12、某校为调查学生参加研究性学习的情况,从全校学生中随机抽取名学生,其中参加“数学类”的有名,既参加“数学类”又参加“理化类”的有名,“数学类”和“理化类”都没有参加的有名,则该校参加“理化类”研究性学习的学生人数与该校学生总数的比值的估计值是( )
A. B. C. D.
【答案】C
【解析】设参加“数学类”的学生人数构成集合,参加“理化类”的学生人数构成集合,其中只参加“理化类”的学生人数为人,样本100人构成全集,
根据题意,可得,解得,
所以参加“理化类”的学生人数为人,
所以参加“理化类”研究性学习的学生人数与该校学生总数的比值的估计值是.
故选:C.
13、调查了100名携带药品出国的旅游者,其中75人带有感冒药,80人带有胃药,那么对于既带感冒药又带胃药的人数统计中,下列说法正确的是( )
A.最多人数是55 B.最少人数是55 C.最少人数是75 D.最多人数是80
【答案】B
【解析】设100名携带药品出国的旅游者组成全集I,其中带感冒药的人组成集合A,带胃药的人组成集合B.
又设所携带药品既非感冒药又非胃药的人数为x,则x∈[0,20],以上两种药都带的人数为y.
根据题意列出Venn图,如图所示,由图可知,x+75+80-y=100.
所以,y=55+x.,又因为 0≤x≤20,所以,55≤y≤75,故最少人数是55.故选B;
14、设计如下图的四个电路图,则能表示“开关A闭合”是“灯泡B亮”的必要不充分条件的一个电路图是( )
A. B. C. D.
【提示】根据“开关A闭合”是“灯泡B亮”的必要不充分条件判断出:开关A闭合推不出灯泡B亮,但灯泡B亮能推出开关A闭合,从而选出选项.
【答案】C;
【解析】选项A:“开关A闭合”是“灯泡B亮”的充分不必要条件;
选项B:“开关A闭合”是“灯泡B亮”的充要条件;
选项C:“开关A闭合”是“灯泡B亮”的必要不充分条件;
选项D:“开关A闭合”是“灯泡B亮”的既不充分也不必要条件.
故选:C.
三、解答题(共4小题,满分44分;请在答题卡指定区域内作答,解答时应写出文字说明、证明过程或演算步骤)
15.(本题8分)
某班45名学生参加“3·12”植树节活动,每位学生都参加除草 植树两项劳动.依据劳动表现,评定为“优秀” “合格”2个等级,结果如下表:
等级项目 优秀 合格 合计
除草 30 15 45
植树 20 25 45
若在两个项目中都“合格”的学生最多有10人,求在两个项目中都“优秀”的最多的人数。
【提示】用集合表示除草优秀的学生,表示椿树优秀的学生,全班学生用全集表示,则表示除草合格的学生,则表示植树合格的学生,作出Venn图,易得它们的关系,从而得出结论;
【答案】15;
【解析】用集合表示除草优秀的学生,表示椿树优秀的学生,全班学生用全集表示,则表示除草合格的学生,则表示植树合格的学生,作出Venn图,如图,
设两个项目都优秀的人数为,两个项目都是合格的人数为,由图可得,,因为,所以;
【说明】集合与逻辑问题中 遇到涉及集合运算与元素个数问题,文氏图可以直观地帮助分析、列式与结合限制条件解之。
16.(本题10分)
当两个集合中一个集合为另一集合的子集时,称这两个集合构成“全食”;当两个集合有公共元素,但互不为对方子集时,称这两个集合构成“偏食”.对于集合A=,B={x|ax2=1,a≥0},若A与B构成“全食”或构成“偏食”,求a的取值构成的集合。
【答案】{0,1,4}
【解析】因为,B={x|ax2=1,a≥0},
所以,当a=0时,B为空集,此时满足B A,
所以,集合A与B构成“全食”;
若a>0,则B=.由题意知=1或=,
当=1时,B={1,-1},B A,A与B构成“全食”;
当=时,B=,A与B构成“偏食”.
解得a=1或a=4.综上,a的取值集合为{0,1,4}.
17.(本题满分12分)已知非空集合A,B满足以下两个条件:
①,;
②A的元素个数不是A中的元素,B的元素个数不是B中的元素,
求:有序集合对的个数。
【答案】8;
【解析】由题意,符合要求的情况分为以下几类:
(1)当集合A只有一个元素时,集合B中有四个元素,且,
故,,共计1种;
(2)当集合A有两个元素时,集合B中有三个元素,且,
故可能结果为:①,;②,;
③,,共计3种;
(3)当集合A有三个元素时,集合B中有两个元素,且,
故可能结果为:①,;②,;
③,,共计3种;
(4)当集合A中有4个元素时,集合B中有1个元素,且,
故,,共计1种.
所以有序集合对的个数为.
18.(本题满分14分、第1小题满分6分、第2小题满分8分)
在①、②、③这三个条件中任选一个,补充在下面横线上,求解下列问题:
设集合___________,集合,
(1)定义且,当时,求;
(2)若,求实数的取值范围.
注:如果选择多个条件分别解答,按第一个解答计分.
【答案】(1);(2).
【解析】
选①:
(1),若,则,即,解得,
若,,无解,
则的解集为,,
,即,解得,,
则.
(2)因为,所以,即,,
因为,所以,解得,的取值范围为.
选②:
(1),解得,,
,即,解得,,
则.
(2)因为,所以,即,,
因为,所以,解得,的取值范围为.
选③:
(1),,解得,,
,即,解得,,
则.
(2)因为,所以,即,,
因为,所以,解得,的取值范围为.
【说明】本题属于“集合中的结构不良问题”;综合考查学生的命题构成与结合教材概念、公式与推导思路、过程进行推导、论证的能力;
①
②
③
④
①
②
③
④
