2.2整式的加减 课后练习2020-2021学年沪科版七年级数学上册(Word版 含答案)
文档属性
| 名称 | 2.2整式的加减 课后练习2020-2021学年沪科版七年级数学上册(Word版 含答案) |

|
|
| 格式 | docx | ||
| 文件大小 | 286.6KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 沪科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-10-19 14:38:29 | ||
图片预览



文档简介
整式的加减
一、单选题
1.下列式子:
(1)和;(2)和;(3)和;(4)和;(5)和;(6)和3.其中,是同类项的是( )
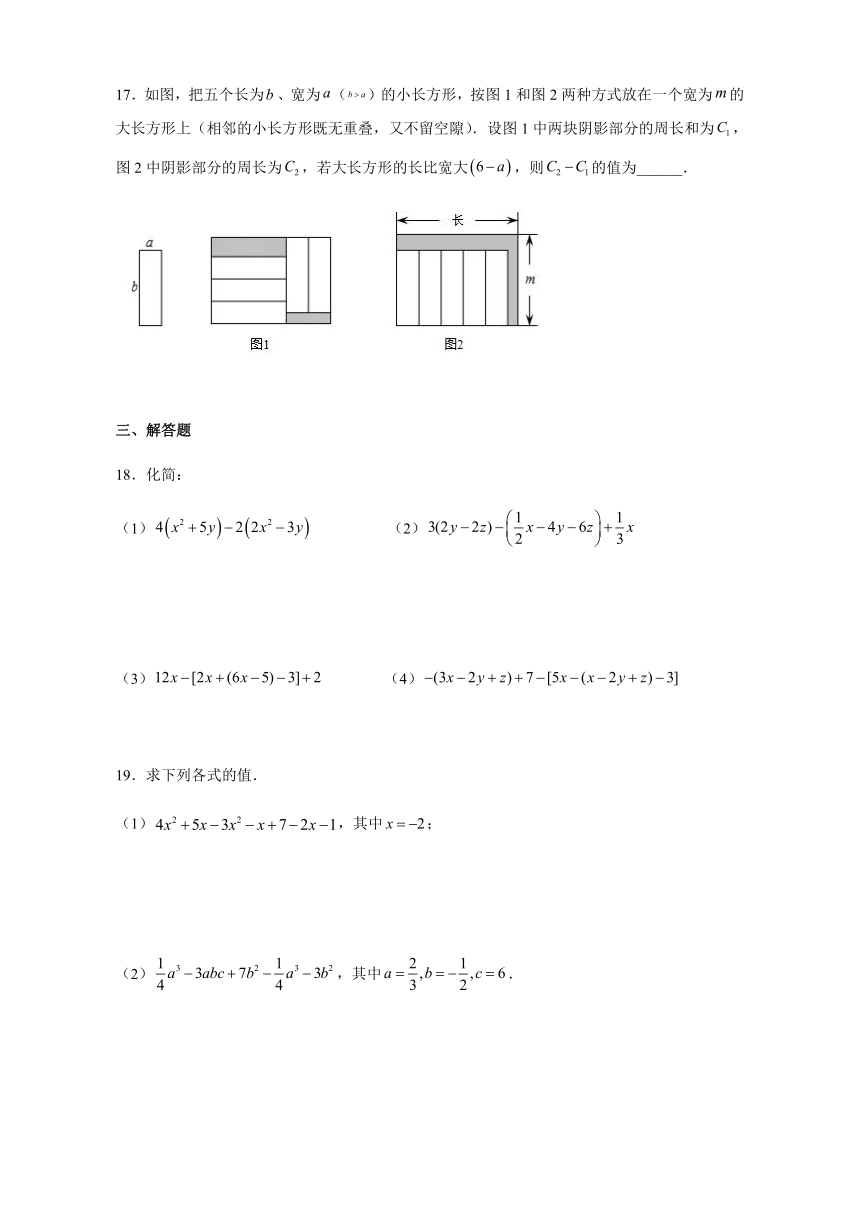
A.(1)(2)(3) B.(2)(4)(5)(6) C.(2)(5)(6) D.(4)(5)(6)
2.已知单项式与可以合并同类项,则m,n分别为( )
A.1,2 B.3,2 C.1,0 D.3,0
3.下列运算正确的是( )
A.3a+2b=5ab B.﹣y2﹣y=﹣y3
C.5a2b﹣3ba2=2a2b D.﹣(6x+2y)=﹣6x+2y
4.如果关于y的整式合并同类项后为零,则有理数a、b的关系是( ).
A.相等 B.都是零 C.互为相反数 D.可为任意数
5.把多项式合并同类项后所得的结果是( ).
A.二次三项式 B.二次二项式 C.一次二项式 D.单项式
6.化简的结果是( )
A. B. C. D.
7.下列各式中,去括号错误的是( )
A.abcabc B.abcabc
C.abcabc D.abcabc
8.不改变多项式的值,把后三项放在前面是“—”号的括号中,正确的是( )
A. B.
C. D.
9.将多项式按字母的降幂排列正确的是( )
A. B.
C. D.
10.若,,则的值为( ).
A. B. C. D.
11.当时,多项式与的和是( )
A.0 B.4 C. D.
12.多项式与相加后不含二次项,则常数m的值是( )
A. B.3 C. D.
二、填空题
13.若单项式与的和为单项式,则______,_______.
14.如果多项式中不含的项,则k的值为______
15.有一道题的部分条件为:长方体的长宽高均为整数,将长宽高都增加1后,求长方体增加的表面积.四位同学做出来的答案分别为:14、103、214、400,已知有一位同学的答案是正确答案,那么正确答案为__________.
16.多项式﹣3x2﹣2xy2+x3y+4x4y3+5按x降幂排列得到______.
17.如图,把五个长为、宽为()的小长方形,按图1和图2两种方式放在一个宽为的大长方形上(相邻的小长方形既无重叠,又不留空隙).设图1中两块阴影部分的周长和为,图2中阴影部分的周长为,若大长方形的长比宽大,则的值为______.
三、解答题
18.化简:
(1) (2)
(3) (4)
19.求下列各式的值.
(1),其中;
(2),其中.
20.规定:,如:.
(1)求的值;
(2)若,求的值;
(3)的绝对值为,若,求的值.
21.如图,长为32米,宽为20米的长方形地面上,修筑宽度均为x米的两条互相垂直的小路(图中阴影部分),余下的部分作为耕地,如果将两条小路铺上地砖,选用地砖的价格是每平米40元.
(1)求买地砖至少需要多少元?(用含x的式子表示)
(2)计算当x=2时,地砖的费用.
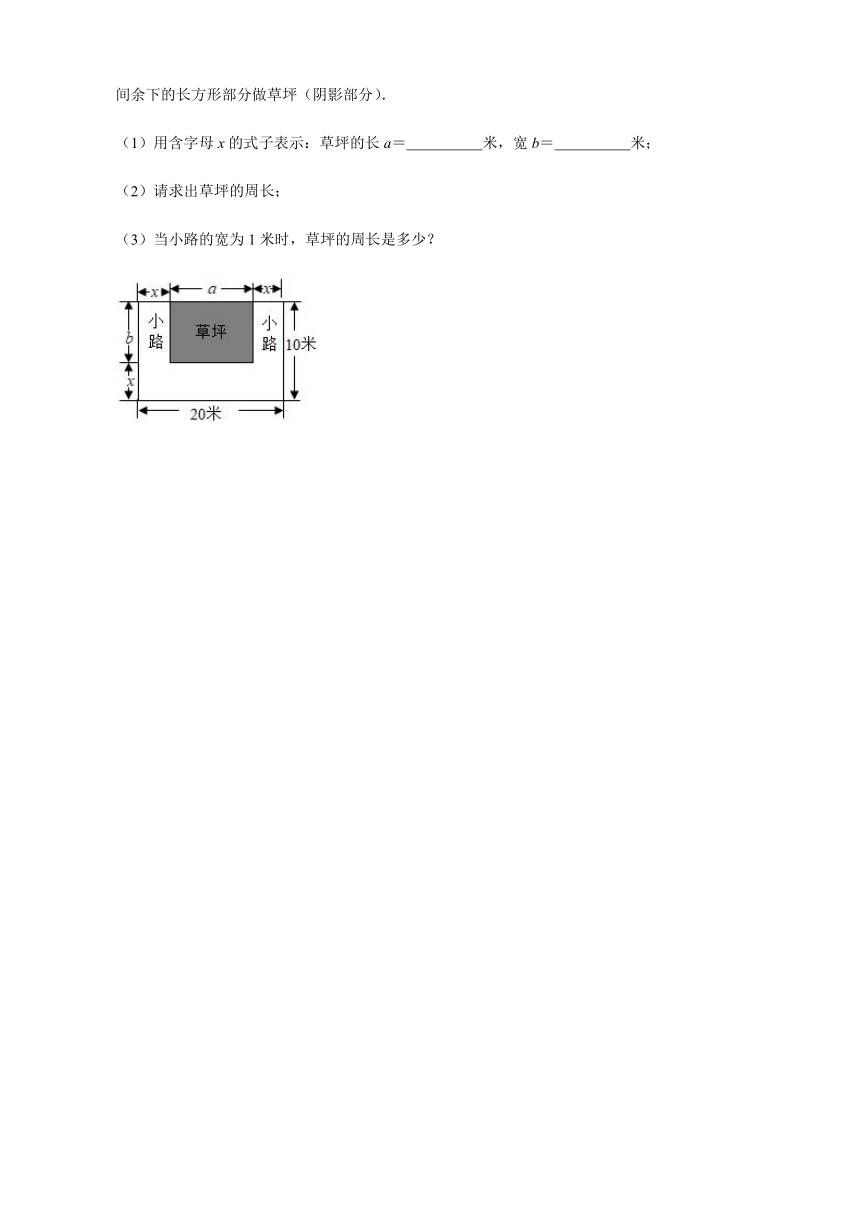
22.如图,有一块长为20米,宽为10米的长方形土地,现在将三面留出宽都是x米的小路,中间余下的长方形部分做草坪(阴影部分).
(1)用含字母x的式子表示:草坪的长a= 米,宽b= 米;
(2)请求出草坪的周长;
(3)当小路的宽为1米时,草坪的周长是多少?
参考答案
1.C
解:(1)中含有的字母不同,(3)中后一个单项式缺少字母x,(4)中相同字母的指数不同,
所以(1)(3)(4)均不是同类项,
(2)(5)(6)所含字母相同,并且相同字母的指数也相同
所以(2)(5)(6)是同类项,
故选:C.
2.A
解:由题意可知:m+1=2,n-1=1,
∴m=1,n=2,
故选:A.
3.C
解:A、3a+2b不能合并,故本选项错误;
B、﹣y2﹣y不能合并,故本选项错误;
C、5a2b﹣3ba2=2a2b,故本选项正确;
D、﹣(6x+2y)=﹣6x﹣2y,故本选项错误;
故选:C.
4.C
解:ay+by=0 则a+b=0
∴a=-b
∴a,b互为相反数
故选C
5.B
解:
.
最高次为2,项数为2,即为二次二项式.
故选B.
6.B
解:.
故选:B.
7.D
解:A选项,原式=a+b﹣c,故该选项计算正确;
B选项,原式=a﹣b+c,故该选项计算正确;
C选项,原式=a﹣b+c,故该选项计算正确;
D选项,原式=a+b+c,故该选项计算错误;
故选:D.
8.A
解:3b3-2ab2+4a2b-a3=3b3-(2ab2-4a2b+a3);
故选:A.
9.B
解:根据题意,
按字母的降幂排列正确的是;
故选:B.
10.C
解:,故不符合题意;
,故不符合题意;
,故符合题意;
,故不符合题意;
故选:
11.D
解:根据题意,
.
当时,
原式.
故选:D.
12.A
解:36x2-3x+5+3x3+12mx2-5x+7
=3x3+(36+12m)x2-8x+12,
∵多项式36x2-3x+5与3x3+12mx2-5x+7相加后,不含二次项,
∴36+12m=0,
解得,m=-3,
故选:A.
13.2 4
解:单项式与的和为单项式,
解得
故答案为:;.
14.
解:,
∵多项式不含项,
∴,
解得:.
故答案为:.
15.214
解:设长方体的长、宽、高分别为:、、,
则原长方体的表面积为:,
增加以后长方体的表面积为:,
则增加的表面积为:,
∵长方体的长宽高均为整数,
∴也为整数,且,
∴当增加的表面积为14时,,
解得:,不合题意,舍去;
当增加的表面积为103时:,
解得:,不合题意,舍去;
当增加的表面积为214时:,
解得:,符合题意;
当增加的表面积为400时:,
解得:,不合题意,舍去;
故答案为:214.
16.4x4y3+x3y﹣3x2﹣2xy2+5
解:多项式﹣3x2﹣2xy2+x3y+4x4y3+5按x的降幂排列为:
4x4y3+x3y﹣3x2﹣2xy2+5.
故答案为:4x4y3+x3y﹣3x2﹣2xy2+5.
17.12
解:由图可知
∴
又
∴
故答案为12.
18.(1);(2);(3);(4)
解:(1)原式;
(2)原式;
(3)原式;
(4)原式;
19.(1),6;(2),7.
解:(1)
,
当时,
原式;
(2)
,
当时,
原式
.
20.(1)5;(2)9;(3)或
解:(1)∵,
∴;
(2)∵,
∴,
∴,
∴===9;
(3)∵,
∴,
∴或,
解得:或.
21.(1)(2080x﹣40x2)元;(2)4000元
解:(1)小路的面积为:32x+20x﹣x2,即52x﹣x2(平方米),
买地砖的金额为:40×(52x﹣x2)=2080x﹣40x2(元),
答:买地砖至少需要(2080x﹣40x2)元;
(2)当x=2时,
2080x﹣40x2=2080×2﹣40×22
=4160﹣160
=4000(元),
答:当x=2时,地砖的费用为4000元.
22.(1)20﹣2x,10﹣x;(2)(60﹣6x)米;(3)54米
解:(1)由图形所反映的草坪的长a,宽b,路的宽x与原长方形的长20m,宽10m之间关系得,
a=20﹣2x,b=10﹣x,
故答案为:20﹣2x,10﹣x;
(2)由长方形的周长公式得,
[(20﹣2x)+(10﹣x)]×2=60﹣6x(米),
答:长方形的周长为(60﹣6x)米;
(3)当x=1时,60﹣6x=60﹣6=54(米),
答:当小路的宽为1米时,草坪的周长是54米.
一、单选题
1.下列式子:
(1)和;(2)和;(3)和;(4)和;(5)和;(6)和3.其中,是同类项的是( )
A.(1)(2)(3) B.(2)(4)(5)(6) C.(2)(5)(6) D.(4)(5)(6)
2.已知单项式与可以合并同类项,则m,n分别为( )
A.1,2 B.3,2 C.1,0 D.3,0
3.下列运算正确的是( )
A.3a+2b=5ab B.﹣y2﹣y=﹣y3
C.5a2b﹣3ba2=2a2b D.﹣(6x+2y)=﹣6x+2y
4.如果关于y的整式合并同类项后为零,则有理数a、b的关系是( ).
A.相等 B.都是零 C.互为相反数 D.可为任意数
5.把多项式合并同类项后所得的结果是( ).
A.二次三项式 B.二次二项式 C.一次二项式 D.单项式
6.化简的结果是( )
A. B. C. D.
7.下列各式中,去括号错误的是( )
A.abcabc B.abcabc
C.abcabc D.abcabc
8.不改变多项式的值,把后三项放在前面是“—”号的括号中,正确的是( )
A. B.
C. D.
9.将多项式按字母的降幂排列正确的是( )
A. B.
C. D.
10.若,,则的值为( ).
A. B. C. D.
11.当时,多项式与的和是( )
A.0 B.4 C. D.
12.多项式与相加后不含二次项,则常数m的值是( )
A. B.3 C. D.
二、填空题
13.若单项式与的和为单项式,则______,_______.
14.如果多项式中不含的项,则k的值为______
15.有一道题的部分条件为:长方体的长宽高均为整数,将长宽高都增加1后,求长方体增加的表面积.四位同学做出来的答案分别为:14、103、214、400,已知有一位同学的答案是正确答案,那么正确答案为__________.
16.多项式﹣3x2﹣2xy2+x3y+4x4y3+5按x降幂排列得到______.
17.如图,把五个长为、宽为()的小长方形,按图1和图2两种方式放在一个宽为的大长方形上(相邻的小长方形既无重叠,又不留空隙).设图1中两块阴影部分的周长和为,图2中阴影部分的周长为,若大长方形的长比宽大,则的值为______.
三、解答题
18.化简:
(1) (2)
(3) (4)
19.求下列各式的值.
(1),其中;
(2),其中.
20.规定:,如:.
(1)求的值;
(2)若,求的值;
(3)的绝对值为,若,求的值.
21.如图,长为32米,宽为20米的长方形地面上,修筑宽度均为x米的两条互相垂直的小路(图中阴影部分),余下的部分作为耕地,如果将两条小路铺上地砖,选用地砖的价格是每平米40元.
(1)求买地砖至少需要多少元?(用含x的式子表示)
(2)计算当x=2时,地砖的费用.
22.如图,有一块长为20米,宽为10米的长方形土地,现在将三面留出宽都是x米的小路,中间余下的长方形部分做草坪(阴影部分).
(1)用含字母x的式子表示:草坪的长a= 米,宽b= 米;
(2)请求出草坪的周长;
(3)当小路的宽为1米时,草坪的周长是多少?
参考答案
1.C
解:(1)中含有的字母不同,(3)中后一个单项式缺少字母x,(4)中相同字母的指数不同,
所以(1)(3)(4)均不是同类项,
(2)(5)(6)所含字母相同,并且相同字母的指数也相同
所以(2)(5)(6)是同类项,
故选:C.
2.A
解:由题意可知:m+1=2,n-1=1,
∴m=1,n=2,
故选:A.
3.C
解:A、3a+2b不能合并,故本选项错误;
B、﹣y2﹣y不能合并,故本选项错误;
C、5a2b﹣3ba2=2a2b,故本选项正确;
D、﹣(6x+2y)=﹣6x﹣2y,故本选项错误;
故选:C.
4.C
解:ay+by=0 则a+b=0
∴a=-b
∴a,b互为相反数
故选C
5.B
解:
.
最高次为2,项数为2,即为二次二项式.
故选B.
6.B
解:.
故选:B.
7.D
解:A选项,原式=a+b﹣c,故该选项计算正确;
B选项,原式=a﹣b+c,故该选项计算正确;
C选项,原式=a﹣b+c,故该选项计算正确;
D选项,原式=a+b+c,故该选项计算错误;
故选:D.
8.A
解:3b3-2ab2+4a2b-a3=3b3-(2ab2-4a2b+a3);
故选:A.
9.B
解:根据题意,
按字母的降幂排列正确的是;
故选:B.
10.C
解:,故不符合题意;
,故不符合题意;
,故符合题意;
,故不符合题意;
故选:
11.D
解:根据题意,
.
当时,
原式.
故选:D.
12.A
解:36x2-3x+5+3x3+12mx2-5x+7
=3x3+(36+12m)x2-8x+12,
∵多项式36x2-3x+5与3x3+12mx2-5x+7相加后,不含二次项,
∴36+12m=0,
解得,m=-3,
故选:A.
13.2 4
解:单项式与的和为单项式,
解得
故答案为:;.
14.
解:,
∵多项式不含项,
∴,
解得:.
故答案为:.
15.214
解:设长方体的长、宽、高分别为:、、,
则原长方体的表面积为:,
增加以后长方体的表面积为:,
则增加的表面积为:,
∵长方体的长宽高均为整数,
∴也为整数,且,
∴当增加的表面积为14时,,
解得:,不合题意,舍去;
当增加的表面积为103时:,
解得:,不合题意,舍去;
当增加的表面积为214时:,
解得:,符合题意;
当增加的表面积为400时:,
解得:,不合题意,舍去;
故答案为:214.
16.4x4y3+x3y﹣3x2﹣2xy2+5
解:多项式﹣3x2﹣2xy2+x3y+4x4y3+5按x的降幂排列为:
4x4y3+x3y﹣3x2﹣2xy2+5.
故答案为:4x4y3+x3y﹣3x2﹣2xy2+5.
17.12
解:由图可知
∴
又
∴
故答案为12.
18.(1);(2);(3);(4)
解:(1)原式;
(2)原式;
(3)原式;
(4)原式;
19.(1),6;(2),7.
解:(1)
,
当时,
原式;
(2)
,
当时,
原式
.
20.(1)5;(2)9;(3)或
解:(1)∵,
∴;
(2)∵,
∴,
∴,
∴===9;
(3)∵,
∴,
∴或,
解得:或.
21.(1)(2080x﹣40x2)元;(2)4000元
解:(1)小路的面积为:32x+20x﹣x2,即52x﹣x2(平方米),
买地砖的金额为:40×(52x﹣x2)=2080x﹣40x2(元),
答:买地砖至少需要(2080x﹣40x2)元;
(2)当x=2时,
2080x﹣40x2=2080×2﹣40×22
=4160﹣160
=4000(元),
答:当x=2时,地砖的费用为4000元.
22.(1)20﹣2x,10﹣x;(2)(60﹣6x)米;(3)54米
解:(1)由图形所反映的草坪的长a,宽b,路的宽x与原长方形的长20m,宽10m之间关系得,
a=20﹣2x,b=10﹣x,
故答案为:20﹣2x,10﹣x;
(2)由长方形的周长公式得,
[(20﹣2x)+(10﹣x)]×2=60﹣6x(米),
答:长方形的周长为(60﹣6x)米;
(3)当x=1时,60﹣6x=60﹣6=54(米),
答:当小路的宽为1米时,草坪的周长是54米.
同课章节目录
- 第1章 有理数
- 1.1 正数和负数
- 1.2 数轴、相反数和绝对值
- 1.3 有理数的大小
- 1.4 有理数的加减
- 1.5 有理数的乘除
- 1.6 有理数的乘方
- 1.7 近似数
- 第2章 整式加减
- 2.1 代数式
- 2.2 整式加减
- 第3章 一次方程与方程组
- 3.1 一元一次方程及其解法
- 3.2 一元一次方程的应用
- 3.3二元一次方程组及其解法
- 3.4 二元一次方程组的应用
- 3.5 三元一次方程组及其解法
- 第4章 直线与角
- 4.1 几何图形
- 4.2 线段、射线、直线
- 4.3 线段的 长短比较
- 4.4 角
- 4.5 角的比较与补(余)角
- 4.6 用尺规作线段与角
- 第5章 数据的收集与整理
- 5.1 数据的 收集
- 5.2 数据的整理
- 5.3 用统计图描述数据
- 5.4 从图表中的数据获取信息
