冀教版2021-2022学年数学九年级上册第25章图形的相似 同步练习题 (word版、含解析)
文档属性
| 名称 | 冀教版2021-2022学年数学九年级上册第25章图形的相似 同步练习题 (word版、含解析) |  | |
| 格式 | doc | ||
| 文件大小 | 440.4KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 冀教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-10-19 15:52:53 | ||
图片预览


文档简介
2021-2022学年冀教版九年级数学上册《第25章图形的相似》同步练习题(附答案)
一.选择题
1.若2a=3b,则=( )
A. B.﹣ C. D.﹣
2.如果,那么的值等于( )
A. B. C. D.2
3.若(3b+d﹣2f≠0),则的值是( )
A.1 B. C.3 D.无法确定
4.下列各组线段中,不是成比例线段的是( )
A.3,6,2,4 B.4,6,5,10 C.1,,, D.2,,,2
5.下列各组线段中,成比例的一组是( )
A.a=4,b=6,c=5,d=10 B.a=2,b=4,c=3,d=6
C.a=2,b=,c=2,d=10 D.a=0.8,b=3,c=1,d=10
6.若ad=bc,则下列不成立的是( )
A.=(b≠0,d≠0)
B.=(b≠0,b≠d)
C.=(b≠0,d≠0)
D.=(b≠﹣1,d≠﹣1)
7.古希腊时期,人们认为最美人体的头顶至肚脐的长度与肚脐至足底的长度之比是(,称为黄金分割比例),著名的“断臂维纳斯”便是如此.若小凡的身高满足此黄金分割比例,且肚脐至足底的长度为108cm,则小凡的身高约为( )
A.155cm B.165cm C.175cm D.185cm
8.已知点B是线段AC的黄金分割点(AB>BC),AC=10,那么AB的长是( )
A. B. C. D.
9.如图,△ABC中,点D,E分别在AB,AC边上,DE∥BC,AD:AB=3:4,则AE:EC的值为( )
A.3:1 B.4:1 C.4:3 D.3:2
10.如图,在△APM的边AP上任取两点B,C,过B作AM的平行线交PM于N,过N作MC的平行线交AP于D.若=,则的值为( )
A. B. C.2 D.3
11.如图,直线l1∥l2∥l3,直线AC和DF被l1,l2,l3所截,如果AB=3,BC=5,EF=4,那么DE的长是( )
A. B. C. D.
12.如图,已知△ADE和△ABC的相似比是1:2,且△ADE的面积是1,则四边形DBCE的面积是( )
A.2 B.3 C.4 D.5
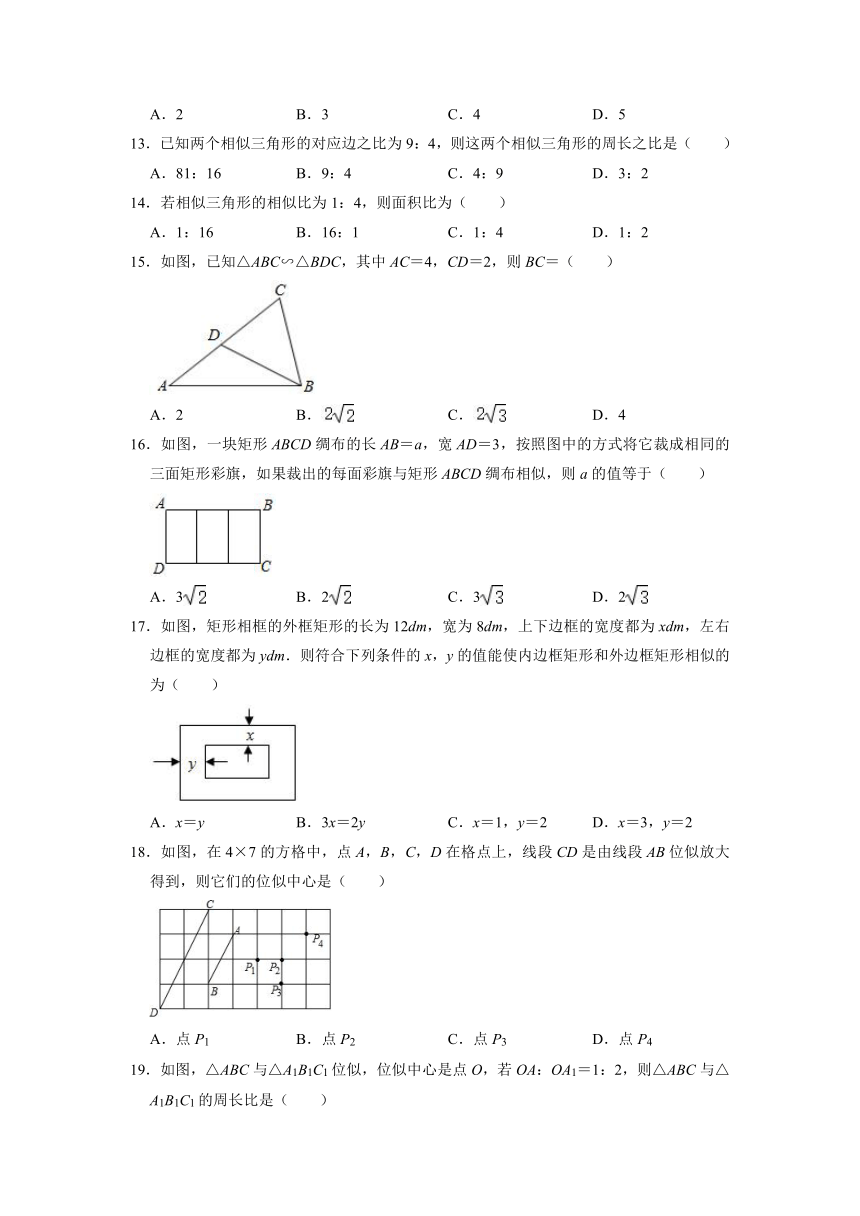
13.已知两个相似三角形的对应边之比为9:4,则这两个相似三角形的周长之比是( )
A.81:16 B.9:4 C.4:9 D.3:2
14.若相似三角形的相似比为1:4,则面积比为( )
A.1:16 B.16:1 C.1:4 D.1:2
15.如图,已知△ABC∽△BDC,其中AC=4,CD=2,则BC=( )
A.2 B. C. D.4
16.如图,一块矩形ABCD绸布的长AB=a,宽AD=3,按照图中的方式将它裁成相同的三面矩形彩旗,如果裁出的每面彩旗与矩形ABCD绸布相似,则a的值等于( )
A.3 B.2 C.3 D.2
17.如图,矩形相框的外框矩形的长为12dm,宽为8dm,上下边框的宽度都为xdm,左右边框的宽度都为ydm.则符合下列条件的x,y的值能使内边框矩形和外边框矩形相似的为( )
A.x=y B.3x=2y C.x=1,y=2 D.x=3,y=2
18.如图,在4×7的方格中,点A,B,C,D在格点上,线段CD是由线段AB位似放大得到,则它们的位似中心是( )
A.点P1 B.点P2 C.点P3 D.点P4
19.如图,△ABC与△A1B1C1位似,位似中心是点O,若OA:OA1=1:2,则△ABC与△A1B1C1的周长比是( )
A.1:2 B.1:3 C.1:4 D.1:
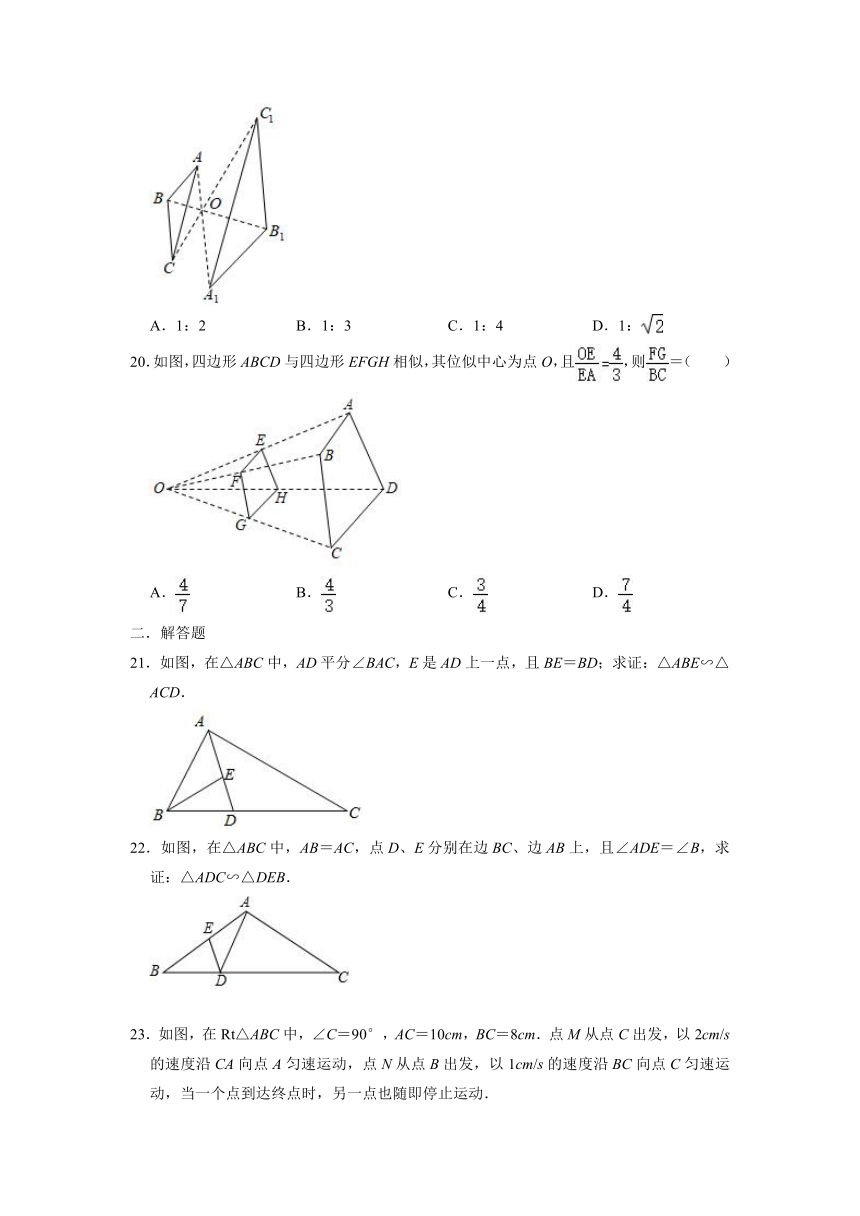
20.如图,四边形ABCD与四边形EFGH相似,其位似中心为点O,且,则=( )
A. B. C. D.
二.解答题
21.如图,在△ABC中,AD平分∠BAC,E是AD上一点,且BE=BD;求证:△ABE∽△ACD.
22.如图,在△ABC中,AB=AC,点D、E分别在边BC、边AB上,且∠ADE=∠B,求证:△ADC∽△DEB.
23.如图,在Rt△ABC中,∠C=90°,AC=10cm,BC=8cm.点M从点C出发,以2cm/s的速度沿CA向点A匀速运动,点N从点B出发,以1cm/s的速度沿BC向点C匀速运动,当一个点到达终点时,另一点也随即停止运动.
(1)经过几秒后,△MCN的面积等于△ABC面积的?
(2)经过几秒,△MCN与△ABC相似?
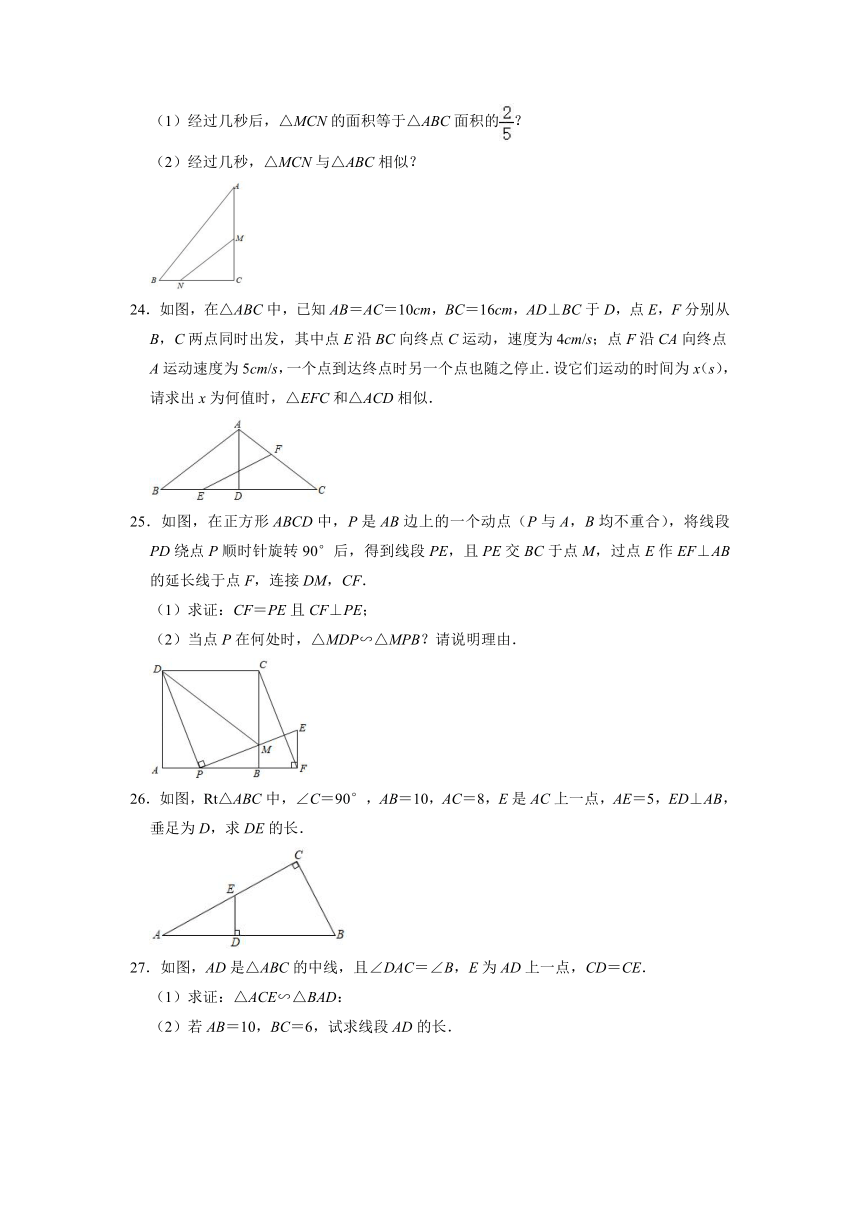
24.如图,在△ABC中,已知AB=AC=10cm,BC=16cm,AD⊥BC于D,点E,F分别从B,C两点同时出发,其中点E沿BC向终点C运动,速度为4cm/s;点F沿CA向终点A运动速度为5cm/s,一个点到达终点时另一个点也随之停止.设它们运动的时间为x(s),请求出x为何值时,△EFC和△ACD相似.
25.如图,在正方形ABCD中,P是AB边上的一个动点(P与A,B均不重合),将线段PD绕点P顺时针旋转90°后,得到线段PE,且PE交BC于点M,过点E作EF⊥AB的延长线于点F,连接DM,CF.
(1)求证:CF=PE且CF⊥PE;
(2)当点P在何处时,△MDP∽△MPB?请说明理由.
26.如图,Rt△ABC中,∠C=90°,AB=10,AC=8,E是AC上一点,AE=5,ED⊥AB,垂足为D,求DE的长.
27.如图,AD是△ABC的中线,且∠DAC=∠B,E为AD上一点,CD=CE.
(1)求证:△ACE∽△BAD:
(2)若AB=10,BC=6,试求线段AD的长.
28.如图,AD是△ABC的高,点P、Q在BC边上,点R在AC边上,点S在AB边上,BC=80,AD=60,四边形PQRS是由两个并排放置的正方形所组成的矩形,则矩形的面积为多少?
29.真身宝塔,位于陕西省扶风法门镇法门寺内,因塔下藏有佛祖真身舍利而得名.小玲和晓静很想知道真身宝塔的高度PQ,于是,有一天,他们带着标杆和皮尺来到法门寺进行测量,测量方案如下:如图,首先,小玲在C处放置一平面镜,她从点C沿QC后退,当退行1.8米到B处时,恰好在镜子中看到塔顶P的像,此时测得小玲眼睛到地面的距离AB为1.5米;然后,晓静在F处竖立了一根高1.6米的标杆EF,发现地面上的点M、标杆顶点E和塔顶P在一条直线上,此时测得FM为2.4米,CF为11.7米,已知PQ⊥QM,AB⊥QM,EF⊥QM,点Q、C、B、F、M在一条直线上,请根据以上所测数据,计算真身宝塔的高度PQ.
30.如图,为了估计河的宽度,在河的对岸选定一个目标点P,在近岸取点Q和S,使点P、Q、S在一条直线上,且直线PS与河垂直,在过点S且与直线PS垂直的直线a上选择适当的点T,PT与过点Q且与PS垂直的直线b的交点为R.如果QS=60m,ST=120m,QR=80m,求PQ的长.
31.如图,利用标杆DE测量楼高,点A,D,B在同一直线上,DE⊥AC,BC⊥AC,垂足分别为E,C.若测得AE=1m,DE=1.5m,CE=5m,楼高BC是多少?
32.如图,△ABC的三个顶点都在方格纸的格点上,请按要求在方格纸内作图.
(1)在图1中以点B为位似中心,作△ABC的位似图形,并把△ABC的边长缩小到原来的.
(2)在图2中画格点线段EF(端点在格点上),把△ABC的面积分为1:2两部分,其中点E,F均落在△ABC的边上且不与点A,B,C重合.
参考答案
1.解:∵2a=3b,
∴=.
故选:A.
2.解:∵,
∴3(a﹣b)=a,
∴a=b,
∴==.
故选:B.
3.解:∵(3b+d﹣2f≠0),
∴a=3b,c=3d,e=3f,
∴===3.
故选:C.
4.解:A、6×2=3×4,成比例线段,故本选项不符合题意;
B、4×10≠5×6,不是成比例线段,故本选项符合题意;
C、1×=×,成比例线段,故本选项不符合题意;
D、2×=×2,成比例线段,故本选项不符合题意.
故选:B.
5.解:A. ==,==,则≠,所以A选项不符合题意;
B. ==,==,则=,所以B选项符合题意;
C. ==,==,则≠,所以C选项不符合题意;
D. ==0.8,==0.3,则≠,所以D选项不符合题意.
故选:B.
6.解:A、∵=,
∴ad=bc,故选项成立;
B、∵=,
∴b(a﹣c)=a(b﹣d),
∴ab﹣bc=ab﹣ad,
∴ad=bc,故选项成立;
C、∵=,
∴(a+b)d=(c+d)b,
∴ad+bd=bc+bd,
∴ad=bc,故选项成立;
D、∵=,
∴(a+1)(d+1)=(b+1)(c+1),
∴ad+a+d+1=bc+b+c+1,
∴ad+a+d=bc+b+c,故选项不成立.
故选:D.
7.解:设小凡的头顶至肚脐的长度为xcm,则小凡的身高为(x+108)cm,
由题意得:=,
∴x≈0.618×108=66.744(cm),
∴x+108≈175(cm),
即小凡的身高约为175cm,
故选:C.
8.解:∵点B是线段AC的黄金分割点(AB>BC),
∴AB=AC,
∵AC=10,
∴AB=×10=5﹣5,
故选:B.
9.解:∵AD:AB=3:4,
∴AD:DB=3:1,
∵DE∥BC,
∴AE:EC=AD:DB=3:1,
故选:A.
10.解:∵BN∥AM,=,
∴=,
∵DN∥CM,
∴==,
故选:B.
11.解:∵直线l1∥l2∥l3,
∴,
∵AB=3,BC=5,EF=4,
∴,
∴DE=.
故选:A.
12.解:∵△ADE与△ABC的相似比为1:2,
∴△ADE与△ABC的面积比为1:4.
∴△ADE与四边形DBCE的面积比为1:3.
∵△ADE的面积是1,
∴四边形DBCE的面积是3.
故选:B.
13.解:两个相似三角形的对应边之比为9:4,则这两个相似三角形的周长之比9:4.
故选:B.
14.解:两个相似三角形的相似比为1:4,相似三角形面积的比等于相似比的平方是1:16.
故选:A.
15.解:∵△ABC∽△BDC,
∴=,
∵AC=4,CD=2,
∴BC2=AC CD=4×2=8,
∴BC=2.
故选:B.
16.解:∵使裁出的每面彩旗的宽与长的比与原绸布的宽与长的比相同,
∴,
解得a=3或﹣3(舍弃),
∴a=3,
故选:C.
17.解:如图,当矩形ABCD∽矩形EFGH时,则有=,
∴=,
可得3x=2y,选项B符合题意,
当矩形ABCD∽矩形EHFG时,则有=,
∴=,
推不出:x=y或3x=2y或x=1,y=2或x=3,y=2.故选项A,B,C,D都不满足条件,此种情形不存在.
∴矩形ABCD∽矩形EFGH,可得3x=2y,
故选:B.
18.解:延长CA、DB交于点P1,
则点P1为位似中心,
故选:A.
19.解:∵△ABC与△A1B1C1位似,
∴△ABC∽△A1B1C1,AC∥A1C1,
∴△AOC∽△A1OC1,
∴==,
∴△ABC与△A1B1C1的周长比为1:2,
故选:A.
20.解:∵=,
∴=,
∵四边形ABCD与四边形EFGH相似,
∴EF∥AB,FG∥BC,
∴△OEF∽△OAB,△OGF∽△OCB,
∴=,=,
∴==,
故选:A.
21.证明:∵AD平分∠BAC,
∴∠BAD=∠CAD.
∵BE=BD,
∴∠BED=∠BDE.
∴∠AEB=∠ADC.
∴△ABE∽△ACD.
22.证明:在△ABC中,AB=AC,
∴∠B=∠C,
∵∠EDC=∠ADE+∠ADC=∠B+∠BED,∠ADE=∠B,
∴∠DEB=∠ADC,
在△ADC和△DEB中,∠ADC=∠DEB,∠C=∠B,
∴△ADC∽△DEB.
23.解:(1)设经过x秒,△MCN的面积等于△ABC面积的.
×2x(8﹣x)=×8×10×.
解得x1=x2=4.
答:经过4秒后,△MCN的面积等于△ABC面积的;
(2)设经过t秒,△MCN与△ABC相似.
∵∠C=∠C,
∴可分为两种情况:
①=,即=,
解得t=;
②=,即=.
解得t=.
答:经过或秒,△MCN与△ABC相似.
24.解:(1)如图1中,
点F在AC上,点E在BD上时,
①当时,△CFE∽△CDA,
∴,
∴t=,
②当时,即,
∴t=2,
当点F在AC上,点E在CD上时,不存在△EFC和△ACD相似,
综上所述,t=s或2s时,△EFC和△ACD相似.
25.解:(1)证明:在正方形ABCD中,P在边AB上,且∠DPE=∠A=90°,
∴∠APD+∠ADP=∠APD+∠FPE=90°,
∴∠ADP=∠FPE,
∵EF⊥AB,
∴∠PFE=∠A=90°,
在△PEF和△DPA中,
,
∴△PEF≌△DPA(AAS),
∴PF=AD=AB=DC,
又AF∥CD,
∴四边形PFCD是平行四边形,
∴CF=PD=PE,CF∥PD,
∵DP⊥PE,
∴CF⊥PE.
(2)当点P是AB的中点时,△MDP∽△MPB.
理由:∵△MDP∽△MPB,
∴,
∵∠ADP=∠BPM,∠A=∠PBM,
∴△PDA∽△MPB,
∴,
∴,
∴PA=PB,
即点P是边AB的中点,
∴当点P恰好是AB边的中点时,△MDP∽△MPB.
26.解:∵∠C=∠ADE=90°,∠A=∠A,
∴△ADE∽△ACB,
∴,
又∵AB=10,AC=8,
∴CB==6,
∴=,
∴DE=3.
27.证明:(1)∵CD=CE
∴∠CDE=∠CED
∴∠AEC=∠BDA
又∵∠DAC=∠B
∴△ACE∽△BAD;
(2)∵AD是△ABC的中线,
∴CD=BD=CE=BC=3,
∵∠DAC=∠B,
∴∠ACD=∠BCA,
∴△ACD∽△BCA,
∴,
即,
∴AC=3,
∵△ACE∽△BAD,
∴,
即,
∴AD=5.
28.解:∵SR∥BC,
∴△ASR∽△ABC,
∴,
设PS=y,则SR=2y,
即 ,
解得y=24,
∴PS=24,SR=48,
∴矩形PQRS的面积是24×48=1152.
29.解:∵∠PQC=∠ABC=90°,∠PCQ=∠ACB,
∴△PCQ∽△ACB,
∴,
∴,
∴QC=1.2PQ,
∵∠PQF=∠EFM=90°,∠PMQ=∠EMF,
∴△PMQ∽△EMF,
∴,
∴,
即,
∴PQ=47,
答:真身宝塔的高度PQ为47米.
30.解:设PQ=xm,
由题意可知QR∥ST,
∴△PQR∽△PST
∴.
∴,
解得x=120.
∴PQ的长为120m.
31.解:∵DE⊥AC,BC⊥AC,
∴DE∥BC,
∴△ADE∽△ABC,
∴=,
∴=,
∴BC=9(m),
答:楼高BC是9m.
32.解:(1)如图所示:
(2)∵△ABC的面积为×6×4=12,
∴线段EF将△ABC面积分成4和8两部分,
如图所示:
一.选择题
1.若2a=3b,则=( )
A. B.﹣ C. D.﹣
2.如果,那么的值等于( )
A. B. C. D.2
3.若(3b+d﹣2f≠0),则的值是( )
A.1 B. C.3 D.无法确定
4.下列各组线段中,不是成比例线段的是( )
A.3,6,2,4 B.4,6,5,10 C.1,,, D.2,,,2
5.下列各组线段中,成比例的一组是( )
A.a=4,b=6,c=5,d=10 B.a=2,b=4,c=3,d=6
C.a=2,b=,c=2,d=10 D.a=0.8,b=3,c=1,d=10
6.若ad=bc,则下列不成立的是( )
A.=(b≠0,d≠0)
B.=(b≠0,b≠d)
C.=(b≠0,d≠0)
D.=(b≠﹣1,d≠﹣1)
7.古希腊时期,人们认为最美人体的头顶至肚脐的长度与肚脐至足底的长度之比是(,称为黄金分割比例),著名的“断臂维纳斯”便是如此.若小凡的身高满足此黄金分割比例,且肚脐至足底的长度为108cm,则小凡的身高约为( )
A.155cm B.165cm C.175cm D.185cm
8.已知点B是线段AC的黄金分割点(AB>BC),AC=10,那么AB的长是( )
A. B. C. D.
9.如图,△ABC中,点D,E分别在AB,AC边上,DE∥BC,AD:AB=3:4,则AE:EC的值为( )
A.3:1 B.4:1 C.4:3 D.3:2
10.如图,在△APM的边AP上任取两点B,C,过B作AM的平行线交PM于N,过N作MC的平行线交AP于D.若=,则的值为( )
A. B. C.2 D.3
11.如图,直线l1∥l2∥l3,直线AC和DF被l1,l2,l3所截,如果AB=3,BC=5,EF=4,那么DE的长是( )
A. B. C. D.
12.如图,已知△ADE和△ABC的相似比是1:2,且△ADE的面积是1,则四边形DBCE的面积是( )
A.2 B.3 C.4 D.5
13.已知两个相似三角形的对应边之比为9:4,则这两个相似三角形的周长之比是( )
A.81:16 B.9:4 C.4:9 D.3:2
14.若相似三角形的相似比为1:4,则面积比为( )
A.1:16 B.16:1 C.1:4 D.1:2
15.如图,已知△ABC∽△BDC,其中AC=4,CD=2,则BC=( )
A.2 B. C. D.4
16.如图,一块矩形ABCD绸布的长AB=a,宽AD=3,按照图中的方式将它裁成相同的三面矩形彩旗,如果裁出的每面彩旗与矩形ABCD绸布相似,则a的值等于( )
A.3 B.2 C.3 D.2
17.如图,矩形相框的外框矩形的长为12dm,宽为8dm,上下边框的宽度都为xdm,左右边框的宽度都为ydm.则符合下列条件的x,y的值能使内边框矩形和外边框矩形相似的为( )
A.x=y B.3x=2y C.x=1,y=2 D.x=3,y=2
18.如图,在4×7的方格中,点A,B,C,D在格点上,线段CD是由线段AB位似放大得到,则它们的位似中心是( )
A.点P1 B.点P2 C.点P3 D.点P4
19.如图,△ABC与△A1B1C1位似,位似中心是点O,若OA:OA1=1:2,则△ABC与△A1B1C1的周长比是( )
A.1:2 B.1:3 C.1:4 D.1:
20.如图,四边形ABCD与四边形EFGH相似,其位似中心为点O,且,则=( )
A. B. C. D.
二.解答题
21.如图,在△ABC中,AD平分∠BAC,E是AD上一点,且BE=BD;求证:△ABE∽△ACD.
22.如图,在△ABC中,AB=AC,点D、E分别在边BC、边AB上,且∠ADE=∠B,求证:△ADC∽△DEB.
23.如图,在Rt△ABC中,∠C=90°,AC=10cm,BC=8cm.点M从点C出发,以2cm/s的速度沿CA向点A匀速运动,点N从点B出发,以1cm/s的速度沿BC向点C匀速运动,当一个点到达终点时,另一点也随即停止运动.
(1)经过几秒后,△MCN的面积等于△ABC面积的?
(2)经过几秒,△MCN与△ABC相似?
24.如图,在△ABC中,已知AB=AC=10cm,BC=16cm,AD⊥BC于D,点E,F分别从B,C两点同时出发,其中点E沿BC向终点C运动,速度为4cm/s;点F沿CA向终点A运动速度为5cm/s,一个点到达终点时另一个点也随之停止.设它们运动的时间为x(s),请求出x为何值时,△EFC和△ACD相似.
25.如图,在正方形ABCD中,P是AB边上的一个动点(P与A,B均不重合),将线段PD绕点P顺时针旋转90°后,得到线段PE,且PE交BC于点M,过点E作EF⊥AB的延长线于点F,连接DM,CF.
(1)求证:CF=PE且CF⊥PE;
(2)当点P在何处时,△MDP∽△MPB?请说明理由.
26.如图,Rt△ABC中,∠C=90°,AB=10,AC=8,E是AC上一点,AE=5,ED⊥AB,垂足为D,求DE的长.
27.如图,AD是△ABC的中线,且∠DAC=∠B,E为AD上一点,CD=CE.
(1)求证:△ACE∽△BAD:
(2)若AB=10,BC=6,试求线段AD的长.
28.如图,AD是△ABC的高,点P、Q在BC边上,点R在AC边上,点S在AB边上,BC=80,AD=60,四边形PQRS是由两个并排放置的正方形所组成的矩形,则矩形的面积为多少?
29.真身宝塔,位于陕西省扶风法门镇法门寺内,因塔下藏有佛祖真身舍利而得名.小玲和晓静很想知道真身宝塔的高度PQ,于是,有一天,他们带着标杆和皮尺来到法门寺进行测量,测量方案如下:如图,首先,小玲在C处放置一平面镜,她从点C沿QC后退,当退行1.8米到B处时,恰好在镜子中看到塔顶P的像,此时测得小玲眼睛到地面的距离AB为1.5米;然后,晓静在F处竖立了一根高1.6米的标杆EF,发现地面上的点M、标杆顶点E和塔顶P在一条直线上,此时测得FM为2.4米,CF为11.7米,已知PQ⊥QM,AB⊥QM,EF⊥QM,点Q、C、B、F、M在一条直线上,请根据以上所测数据,计算真身宝塔的高度PQ.
30.如图,为了估计河的宽度,在河的对岸选定一个目标点P,在近岸取点Q和S,使点P、Q、S在一条直线上,且直线PS与河垂直,在过点S且与直线PS垂直的直线a上选择适当的点T,PT与过点Q且与PS垂直的直线b的交点为R.如果QS=60m,ST=120m,QR=80m,求PQ的长.
31.如图,利用标杆DE测量楼高,点A,D,B在同一直线上,DE⊥AC,BC⊥AC,垂足分别为E,C.若测得AE=1m,DE=1.5m,CE=5m,楼高BC是多少?
32.如图,△ABC的三个顶点都在方格纸的格点上,请按要求在方格纸内作图.
(1)在图1中以点B为位似中心,作△ABC的位似图形,并把△ABC的边长缩小到原来的.
(2)在图2中画格点线段EF(端点在格点上),把△ABC的面积分为1:2两部分,其中点E,F均落在△ABC的边上且不与点A,B,C重合.
参考答案
1.解:∵2a=3b,
∴=.
故选:A.
2.解:∵,
∴3(a﹣b)=a,
∴a=b,
∴==.
故选:B.
3.解:∵(3b+d﹣2f≠0),
∴a=3b,c=3d,e=3f,
∴===3.
故选:C.
4.解:A、6×2=3×4,成比例线段,故本选项不符合题意;
B、4×10≠5×6,不是成比例线段,故本选项符合题意;
C、1×=×,成比例线段,故本选项不符合题意;
D、2×=×2,成比例线段,故本选项不符合题意.
故选:B.
5.解:A. ==,==,则≠,所以A选项不符合题意;
B. ==,==,则=,所以B选项符合题意;
C. ==,==,则≠,所以C选项不符合题意;
D. ==0.8,==0.3,则≠,所以D选项不符合题意.
故选:B.
6.解:A、∵=,
∴ad=bc,故选项成立;
B、∵=,
∴b(a﹣c)=a(b﹣d),
∴ab﹣bc=ab﹣ad,
∴ad=bc,故选项成立;
C、∵=,
∴(a+b)d=(c+d)b,
∴ad+bd=bc+bd,
∴ad=bc,故选项成立;
D、∵=,
∴(a+1)(d+1)=(b+1)(c+1),
∴ad+a+d+1=bc+b+c+1,
∴ad+a+d=bc+b+c,故选项不成立.
故选:D.
7.解:设小凡的头顶至肚脐的长度为xcm,则小凡的身高为(x+108)cm,
由题意得:=,
∴x≈0.618×108=66.744(cm),
∴x+108≈175(cm),
即小凡的身高约为175cm,
故选:C.
8.解:∵点B是线段AC的黄金分割点(AB>BC),
∴AB=AC,
∵AC=10,
∴AB=×10=5﹣5,
故选:B.
9.解:∵AD:AB=3:4,
∴AD:DB=3:1,
∵DE∥BC,
∴AE:EC=AD:DB=3:1,
故选:A.
10.解:∵BN∥AM,=,
∴=,
∵DN∥CM,
∴==,
故选:B.
11.解:∵直线l1∥l2∥l3,
∴,
∵AB=3,BC=5,EF=4,
∴,
∴DE=.
故选:A.
12.解:∵△ADE与△ABC的相似比为1:2,
∴△ADE与△ABC的面积比为1:4.
∴△ADE与四边形DBCE的面积比为1:3.
∵△ADE的面积是1,
∴四边形DBCE的面积是3.
故选:B.
13.解:两个相似三角形的对应边之比为9:4,则这两个相似三角形的周长之比9:4.
故选:B.
14.解:两个相似三角形的相似比为1:4,相似三角形面积的比等于相似比的平方是1:16.
故选:A.
15.解:∵△ABC∽△BDC,
∴=,
∵AC=4,CD=2,
∴BC2=AC CD=4×2=8,
∴BC=2.
故选:B.
16.解:∵使裁出的每面彩旗的宽与长的比与原绸布的宽与长的比相同,
∴,
解得a=3或﹣3(舍弃),
∴a=3,
故选:C.
17.解:如图,当矩形ABCD∽矩形EFGH时,则有=,
∴=,
可得3x=2y,选项B符合题意,
当矩形ABCD∽矩形EHFG时,则有=,
∴=,
推不出:x=y或3x=2y或x=1,y=2或x=3,y=2.故选项A,B,C,D都不满足条件,此种情形不存在.
∴矩形ABCD∽矩形EFGH,可得3x=2y,
故选:B.
18.解:延长CA、DB交于点P1,
则点P1为位似中心,
故选:A.
19.解:∵△ABC与△A1B1C1位似,
∴△ABC∽△A1B1C1,AC∥A1C1,
∴△AOC∽△A1OC1,
∴==,
∴△ABC与△A1B1C1的周长比为1:2,
故选:A.
20.解:∵=,
∴=,
∵四边形ABCD与四边形EFGH相似,
∴EF∥AB,FG∥BC,
∴△OEF∽△OAB,△OGF∽△OCB,
∴=,=,
∴==,
故选:A.
21.证明:∵AD平分∠BAC,
∴∠BAD=∠CAD.
∵BE=BD,
∴∠BED=∠BDE.
∴∠AEB=∠ADC.
∴△ABE∽△ACD.
22.证明:在△ABC中,AB=AC,
∴∠B=∠C,
∵∠EDC=∠ADE+∠ADC=∠B+∠BED,∠ADE=∠B,
∴∠DEB=∠ADC,
在△ADC和△DEB中,∠ADC=∠DEB,∠C=∠B,
∴△ADC∽△DEB.
23.解:(1)设经过x秒,△MCN的面积等于△ABC面积的.
×2x(8﹣x)=×8×10×.
解得x1=x2=4.
答:经过4秒后,△MCN的面积等于△ABC面积的;
(2)设经过t秒,△MCN与△ABC相似.
∵∠C=∠C,
∴可分为两种情况:
①=,即=,
解得t=;
②=,即=.
解得t=.
答:经过或秒,△MCN与△ABC相似.
24.解:(1)如图1中,
点F在AC上,点E在BD上时,
①当时,△CFE∽△CDA,
∴,
∴t=,
②当时,即,
∴t=2,
当点F在AC上,点E在CD上时,不存在△EFC和△ACD相似,
综上所述,t=s或2s时,△EFC和△ACD相似.
25.解:(1)证明:在正方形ABCD中,P在边AB上,且∠DPE=∠A=90°,
∴∠APD+∠ADP=∠APD+∠FPE=90°,
∴∠ADP=∠FPE,
∵EF⊥AB,
∴∠PFE=∠A=90°,
在△PEF和△DPA中,
,
∴△PEF≌△DPA(AAS),
∴PF=AD=AB=DC,
又AF∥CD,
∴四边形PFCD是平行四边形,
∴CF=PD=PE,CF∥PD,
∵DP⊥PE,
∴CF⊥PE.
(2)当点P是AB的中点时,△MDP∽△MPB.
理由:∵△MDP∽△MPB,
∴,
∵∠ADP=∠BPM,∠A=∠PBM,
∴△PDA∽△MPB,
∴,
∴,
∴PA=PB,
即点P是边AB的中点,
∴当点P恰好是AB边的中点时,△MDP∽△MPB.
26.解:∵∠C=∠ADE=90°,∠A=∠A,
∴△ADE∽△ACB,
∴,
又∵AB=10,AC=8,
∴CB==6,
∴=,
∴DE=3.
27.证明:(1)∵CD=CE
∴∠CDE=∠CED
∴∠AEC=∠BDA
又∵∠DAC=∠B
∴△ACE∽△BAD;
(2)∵AD是△ABC的中线,
∴CD=BD=CE=BC=3,
∵∠DAC=∠B,
∴∠ACD=∠BCA,
∴△ACD∽△BCA,
∴,
即,
∴AC=3,
∵△ACE∽△BAD,
∴,
即,
∴AD=5.
28.解:∵SR∥BC,
∴△ASR∽△ABC,
∴,
设PS=y,则SR=2y,
即 ,
解得y=24,
∴PS=24,SR=48,
∴矩形PQRS的面积是24×48=1152.
29.解:∵∠PQC=∠ABC=90°,∠PCQ=∠ACB,
∴△PCQ∽△ACB,
∴,
∴,
∴QC=1.2PQ,
∵∠PQF=∠EFM=90°,∠PMQ=∠EMF,
∴△PMQ∽△EMF,
∴,
∴,
即,
∴PQ=47,
答:真身宝塔的高度PQ为47米.
30.解:设PQ=xm,
由题意可知QR∥ST,
∴△PQR∽△PST
∴.
∴,
解得x=120.
∴PQ的长为120m.
31.解:∵DE⊥AC,BC⊥AC,
∴DE∥BC,
∴△ADE∽△ABC,
∴=,
∴=,
∴BC=9(m),
答:楼高BC是9m.
32.解:(1)如图所示:
(2)∵△ABC的面积为×6×4=12,
∴线段EF将△ABC面积分成4和8两部分,
如图所示:
同课章节目录
- 第23章 数据分析
- 23.1 平均数与加权平均数
- 23.2 中位数与众数
- 23.3 方差
- 23.4 用样本估计总体
- 第24章 一元二次方程
- 24.1 一元二次方程
- 24.2 解一元二次方程
- 24.3 一元二次方程根与系数的关系
- 24.4 一元二次方程的应用
- 第25章 图形的相似
- 25.1 比例线段
- 25.2 平行线分线段成比例
- 25.3 相似三角形
- 25.4 相似三角形的判定
- 25.5 相似三角形的性质
- 25.6 相似三角形的应用
- 25.7 相似多边形和图形的位似
- 第26章 解直角三角形
- 26.1 锐角三角函数
- 26.2 锐角三角函数的计算
- 26.3 解直角三角形
- 26.4 解直角三角形的应用
- 第27章 反比例函数
- 27.1 反比例函数
- 27.2 反比例函数的图像和性质
- 27.3 反比例函数的应用
- 第28章 圆
- 28.1 圆的概念和性质
- 28.2 过三点的圆
- 28.3 圆心角和圆周角
- 28.4 垂径定理
- 28.5 弧长和扇形面积
