冀教版2021-2022学年数学九年级上册 第25章图形的相似 同步达标训练 (word版含解析)
文档属性
| 名称 | 冀教版2021-2022学年数学九年级上册 第25章图形的相似 同步达标训练 (word版含解析) |  | |
| 格式 | doc | ||
| 文件大小 | 577.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 冀教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-10-19 17:15:18 | ||
图片预览



文档简介
2021-2022学年冀教版九年级数学上册《第25章图形的相似》同步达标训练(附答案)
一.选择题
1.下面四组线段中,成比例的是( )
A.a=2,b=3,c=4,d=5 B.a=1,b=2,c=2,d=4
C.a=4,b=6,c=8,d=10 D.a=,b=,c=3,d=
2.如果,那么的值等于( )
A. B. C. D.2
3.若(3b+d﹣2f≠0),则的值是( )
A.1 B. C.3 D.无法确定
4.如图,AB与CD相交于点E,点F在线段BC上,且AC∥EF∥DB.若BE=5,BF=3,AE=BC,则的值为( )
A. B. C. D.
5.如图,在△ABC中,D是BC上一点,连接AD,,F是AD的中点,连接BF并延长交AC于E,则的值是( )
A. B. C. D.
6.如图,在四边形ABCD中,已知∠ADC=∠BAC,那么补充下列条件后不能判定△ADC和△BAC相似的是( )
A.CA平分∠BCD B. C.AC2=BC CD D.∠DAC=∠ABC
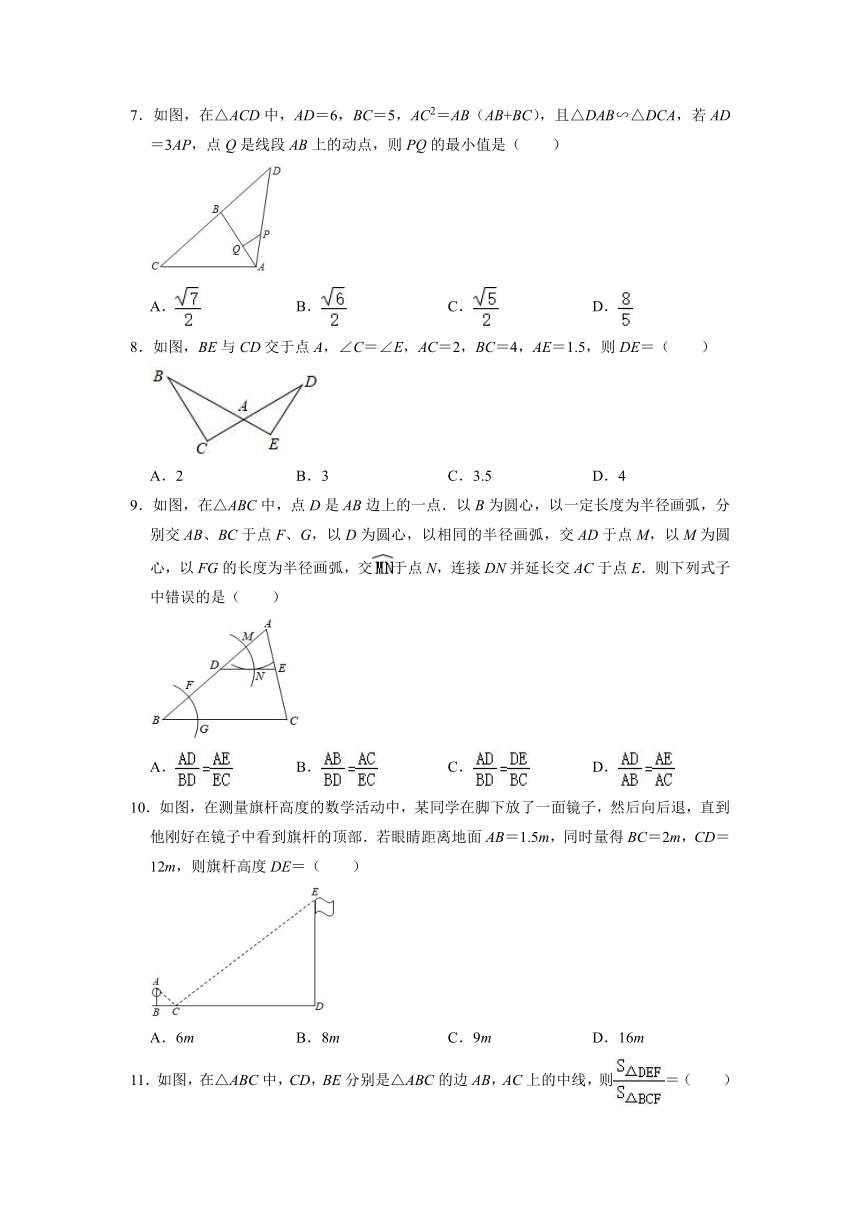
7.如图,在△ACD中,AD=6,BC=5,AC2=AB(AB+BC),且△DAB∽△DCA,若AD=3AP,点Q是线段AB上的动点,则PQ的最小值是( )
A. B. C. D.
8.如图,BE与CD交于点A,∠C=∠E,AC=2,BC=4,AE=1.5,则DE=( )
A.2 B.3 C.3.5 D.4
9.如图,在△ABC中,点D是AB边上的一点.以B为圆心,以一定长度为半径画弧,分别交AB、BC于点F、G,以D为圆心,以相同的半径画弧,交AD于点M,以M为圆心,以FG的长度为半径画弧,交于点N,连接DN并延长交AC于点E.则下列式子中错误的是( )
A. B. C. D.
10.如图,在测量旗杆高度的数学活动中,某同学在脚下放了一面镜子,然后向后退,直到他刚好在镜子中看到旗杆的顶部.若眼睛距离地面AB=1.5m,同时量得BC=2m,CD=12m,则旗杆高度DE=( )
A.6m B.8m C.9m D.16m
11.如图,在△ABC中,CD,BE分别是△ABC的边AB,AC上的中线,则=( )
A. B. C. D.
12.如图所示是利用图形的位似绘制的一幅“小鱼”图案,其中O为位似中心,且OA=2OD,若图案中鱼身(△ABC)的面积为S,则鱼尾(△DEF)的面积为( )
A. B.S C.S D.S
13.如图,已知点C,D都是线段AB的黄金分割点,如果CD=4,那么AB的长度是( )
A.2﹣2 B.6﹣2 C.8+4 D.2+
二.填空题
14.已知(abc≠0,a+b≠c),则= .
15.若===k成立,则k的值为 .
16.若(k≠0),则y=kx+k﹣2一定经过第 象限.
17.如图,点D、E分别在△ABC的边AB,AC上,DE∥BC,点G在边BC上,AG交DE于点H,点O是线段AG的中点,若AD:DB=3:1,则AO:OH= .
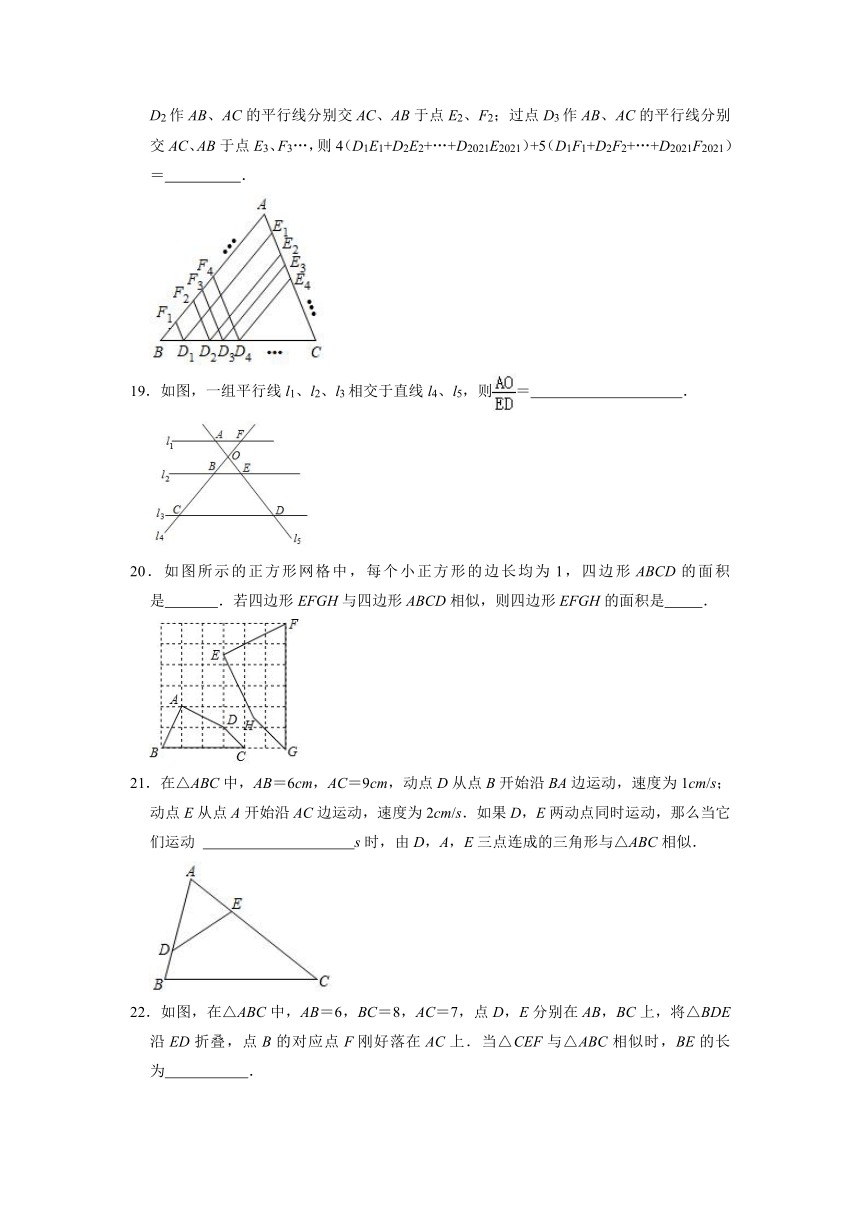
18.如图,在△ABC中,AB=5,AC=4,若进行以下操作,在边BC上从左到右依次取点D1、D2、D3、D4、…;过点D1作AB、AC的平行线分别交AC、AB于点E1、F1;过点D2作AB、AC的平行线分别交AC、AB于点E2、F2;过点D3作AB、AC的平行线分别交AC、AB于点E3、F3…,则4(D1E1+D2E2+…+D2021E2021)+5(D1F1+D2F2+…+D2021F2021)= .
19.如图,一组平行线l1、l2、l3相交于直线l4、l5,则= .
20.如图所示的正方形网格中,每个小正方形的边长均为1,四边形ABCD的面积是 .若四边形EFGH与四边形ABCD相似,则四边形EFGH的面积是 .
21.在△ABC中,AB=6cm,AC=9cm,动点D从点B开始沿BA边运动,速度为1cm/s;动点E从点A开始沿AC边运动,速度为2cm/s.如果D,E两动点同时运动,那么当它们运动 s时,由D,A,E三点连成的三角形与△ABC相似.
22.如图,在△ABC中,AB=6,BC=8,AC=7,点D,E分别在AB,BC上,将△BDE沿ED折叠,点B的对应点F刚好落在AC上.当△CEF与△ABC相似时,BE的长为 .
23.如图,菱形ABCD中,对角线AC与BD相交于点O.将线段AB绕点B顺时针方向旋转,使点A落在BD上的点H.点E为边BC的中点,连接HE,交AC于点P,若AC=12,BD=16,则线段PC的长为 .
24.△AOB三个顶点的坐标分别为A(5,0),O(0,0),B(3,6),以原点O为位似中心,相似比为,将△AOB缩小,则点B的对应点B′的坐标是 .
三.解答题
25.如图1,Rt△ABC中,∠ABC=90°,AB=2BC,D为AC边上一点,BE⊥BD,BE=2BD,连接DE交AB于F点.
(1)求证:△CBD∽△ABE;
(2)若∠DBC=30°,求的值;
(3)如图2,若D在射线AC上,且CD=1,当F点为BE中点时,求AB的值
.
26.如图,在 ABCD中,点E为CD上一点,连接AE,在AE上取一点F,使得∠AFB=∠D.求证:AE BF=BC BA.
27.如图,在平面直角坐标系中,已知△ABC三个顶点的坐标分别为A(﹣1,2),B(﹣3,4),C(﹣2,6).
(1)画出△ABC绕点A顺时针旋转90°后得到的△A1B1C1,写出点C1的坐标.
(2)以原点O为位似中心,画出将△A1B1C1三条边放大为原来的2倍后得△A2B2C2,写出点B2的坐标.
28.如图,在△ABC中,点D、E分别在边AB,AC上,∠AED=∠B,线段AG分别交线段DE,BC于点F,G,且.
(1)求证:△ADF∽△ACG;
(2)若=,求的值.
29.如图,在△ABC中,点D、E分别在边BC、AC上,连接AD、DE.且∠B=∠ADE=∠C.
(1)证明:△BDA∽△CED;
(2)若∠B=45°,BC=6,当点D在BC上运动时(点D不与B、C重合).且△ADE是等腰三角形,求此时BD的长.
30.如图在锐角三角形OAB中,点M,N分别在边OB,OA上,OG⊥AB于点G,OH⊥MN于点H,∠NOH=∠GOB.
(1)求证:△OMN∽△OAB;
(2)若OM=3,OA=7,求的值.
31.如图,在平行四边形ABCD中,点E是AC上一点,射线BE与CD的延长线交于点P,与边AD交于点F,连接FC.
(1)若∠ABF=∠ACF,求证:CE2=EF EP;
(2)若点D是CP中点,BE=2,求EF的长.
32.如图,在△ABC中,CD是角平分线,DE平分∠CDB交BC于点E,且DE∥AC.
(1)求证:CD2=CA CE.
(2)若CE=2BE=2,求CD的长.
33.已知:如图,在Rt△ABC中,∠BAC=90°,AD⊥BC于D,E为直角边AC的中点,过D,E作直线交AB的延长线于F.
(1)若AB=6,AC=8,求BD长;
(2)求证:AB AF=AC DF.
34.如图,在△ABC中,点D,E,F分别在AB,BC,AC边上,DE∥AC,EF∥AB.
(1)求证:△BDE∽△EFC.
(2)若,△EFC的面积是25,求△ABC的面积.
35.如图,在Rt△ABC中,∠C=90°,AC=10cm,BC=8cm.点M从点C出发,以2cm/s的速度沿CA向点A匀速运动,点N从点B出发,以1cm/s的速度沿BC向点C匀速运动,当一个点到达终点时,另一点也随即停止运动.
(1)经过几秒后,△MCN的面积等于△ABC面积的?
(2)经过几秒,△MCN与△ABC相似?
36.如图,在菱形ABCD中,点E,F分别在边BC,DC上,AE与BD交于点H,AE的延长线与DC的延长线交于点G,∠BAE=∠DAF.
(1)求证:AD2=DF DG;
(2)若HE=4,EG=5,求AH的长.
37.如图,小明同学为了测量教学楼的高度OE,先在操场上点A处放一面镜子,从点A处后退1m到点B处,恰好在镜子中看到楼的顶部E点;再将镜子向后移动4m放在C处,从点C处向后退1.5m到点D处,恰好再次在镜子中看到楼的顶部E点,测得小明的眼睛距地面的高度FB,GD为1.5m,点O,A,B,C,D在同一水平线上,镜子可看成一个点.求教学楼的高度OE.
参考答案
1.解:A、2×5≠3×4,故选项不符合题意;
B、1×4=2×2,故选项符合题意;
C、4×10≠5×6,故选项不符合题意;
D、×3≠×,故选项不符合题意.
故选:B.
2.解:∵,
∴3(a﹣b)=a,
∴a=b,
∴==.
故选:B.
3.解:∵(3b+d﹣2f≠0),
∴a=3b,c=3d,e=3f,
∴===3.
故选:C.
4.解:设CF=x,
∵EF∥AC,
∴=,
∴=,
解得x=,
∴CF=,
∵EF∥DB,
∴===.
故选:A.
5.解:过D点作DH∥BE交AC于H,如图,
∵F点为AD的中点,
∴AF=FD,
∵FE∥DH,
∴==1,即AE=EH,
∵DH∥BE,
∴==,CH=3EH,
∴=.
故选:A.
6.解:在△ADC和△BAC中,∠ADC=∠BAC,
如果△ADC∽△BAC,需满足的条件有:
①∠DAC=∠ABC或AC是∠BCD的平分线;
②=;
故选:C.
7.解:∵△DAB∽△DCA,
∴,
∴,
解得:BD=4(负值舍去),
∵△DAB∽△DCA,
∴,
∴AC=,
∵AC2=AB(AB+BC),
∴(AB)2=AB(AB+BC),
∴AB=4,
∴AB=BD=4,
过B作BH⊥AD于H,
∴AH=AD=3,
∴BH===,
∵AD=3AP,AD=6,
∴AP=2,
当PQ⊥AB时,PQ的值最小,
∵∠AQP=∠AHB=90°,∠PAQ=∠BAH,
∴△APQ∽△ABH,
∴,
∴=,
∴PQ=,
故选:A.
8.解:∵∠C=∠E,∠CAB=∠DAE,
∴△CAB∽△EAD,
∴,
∴,
∴DE=3,
故选:B.
9.解:由题意可得:∠ABC=∠ADE,
∴DE∥BC,
∴,,,故选项A,B,D不合题意,
∵DE∥BC,
∴△ADE∽△ABC,
∴,故选项C符合题意,
故选:C.
10.解:∵AB⊥BD,DE⊥BD,
∴∠ABC=∠EDC=90°,
∵∠ACB=∠DCE,
∴△ABC∽△EDC,
∴=,
∴=,
∴DE=9(m),
故选:C.
11.解:∵CD,BE分别是△ABC的边AB,AC上中线,
∴D是AB的中点,E是AC的中点,
∴DE是△ABC的中位线,
∴DE∥BC,DE=BC,
∴△DEF∽△CBF,
∴==,
故选:D.
12.解:∵△ABC与△DEF是以O为位似中心位似图形,OA=2OD,
∴△ABC∽△DEF,且相似比为2,
∴=22=4,
∵△ABC的面积为S,
∴△DEF的面积S,
故选:C.
13.解:∵点C,D都是线段AB的黄金分割点,
∴AD=AB,BC=AB,
∵CD=4,AD+BC﹣CD=AB,
∴AB+AB﹣4=AB,
解得:AB=8+4,
故选:C.
14.解:设=k,
则a=2k,b=3k,c=4k,
所以
=
=
=3,
故答案为:3.
15.解:当a+b+c≠0时,根据比例的等比性质,得k==1:
当a+b+c=0时,即a+b=﹣c,则k==﹣2.
故答案为:1或﹣2.
16.解:根据比例的等比性质,得k=,
当a+b+c≠0时,k=2,
∴直线解析式是y=2x,
∴图象经过一、三象限.
当a+b+c=0时,a+b=﹣c,
∴k===﹣1,
∴直线解析式是y=﹣x﹣3,
∴图象经过二、三、四象限.
综上所述,直线一定经过第三象限,
故答案为:三.
17.解:∵点O是线段AG的中点,
∴OA=OG=AG,
∵DE∥BC,AD:DB=3:1,
∴===,==,
∴OH=OG﹣HG=AG﹣AG=AG,
∴AO:OH=(AG):(AG)=2:1,
故答案为:2:1.
18.解:∵D1F1∥AC,
∴.
∵D1F1∥AC,D1E1∥AB,
∴四边形D1E1AF1为平行四边形.
∴D1E1=AF1.
∴BF1=AB﹣AF1=AB﹣D1E1.
∴.
将AB=5,AC=4代入上式得:4D1E1+5D1F1=20.
同理可得:4D2E2+5D2F2=20,
…
4D2021E2021+5D2021F2021=20,
∴4(D1E1+D2E2+…+D2021E2021)+5(D1F1+D2F2+…+D2021F2021)
=4D1E1+5D1F1+4D2E2+5D2F2+…+4D2021E2021+5D2021F2021
=20+20+…+20
=2021×20
=40420.
故答案为40420.
19.解:∵l1∥l2,
∴=①,
∵l2∥l3,
∴=②,
①×②,得=,
故答案为:.
20.解:∵S四边形ABCD=2×4﹣×1×2﹣×1×2﹣1×1﹣×1×1=.
又∵四边形EFGH与四边形ABCD相似,
∴S四边形EFGH:S四边形ABCD=()2=()2=,
∴S四边形EFGH=×=.
故答案为:,.
21.解:根据题意得:AE=2t,BD=t,
∴AD=6﹣t,
∵∠A=∠A,
∴分两种情况:
①当=时,
即=,解得:t=;
②当=时,
即=,解得:t=;
综上所述:当t=或时,△ADE与△ABC相似.
22.解:∵将△BDE沿DE翻折得到△FDE,
∴BE=EF,
∵BC=8,
∴CE=8﹣BE,
当△CEF与△ABC相似时,=或=,即=或=,
解得:BE=或,
故答案是:或.
23.解:过E点作EF⊥BD于F,
∵四边形ABCD是菱形,
∴AC⊥BD,
∴EF∥AC,
∵AC=12,BD=16,
∴OC=OA=AC=6,OB=OD=BD=8,
∴BC===10,
∴BH=AB=BC=10,
∴OH=BH﹣OB=2,
∵E是BC的中点,EF∥AC,
∴EF=OC=3,OF=OB=4,
∴HF=OH+OF=6,
∵EF∥AC,
∴△HOP∽△HFE,
∴,
∴,
∴OP=1,
∴CP=OC﹣OP=5.
故答案为:5.
24.解:∵△AOB顶点B的坐标为(3,6),以原点O为位似中心,相似比为,将△AOB缩小,
∴点B的对应点B′的坐标为(3×,6×)或(3×(﹣),6×(﹣)),即(2,4)或(﹣2,﹣4),
故答案为:(2,4)或(﹣2,﹣4).
25.解:(1)∵BE⊥BD,
∴∠DBE=90°=∠ABC,
∴∠CBD=∠ABE,
∵AB=2BC,BE=2BD,
∴=,
∴△CBD∽△ABE;
(2)如图1,过点D作DH⊥BC于H,
∵∠ABC=90°,AB=2BC,
∴AC==BC,
∵△CBD∽△ABE,
∴,∠AEB=∠BDC,
∴AE=2CD,
∵DH⊥BC,
∴∠ABC=∠DHC=90°,
又∵∠C=∠C,
∴△ABC∽△DHC,
∴,
∴CH=CD,DH=CD,
∵∠DBC=30°,
∴BD=2DH=CD,
∵∠AEB=∠BDC,∠BDC+∠ADB=180°,
∴∠AEB+∠ADB=180°,
∴点A,点E,点B,点D四点共圆,
∴∠AED=∠ABD,∠BAE=∠BDE,
∴△AEF∽△DBF,
∴,
∴;
(3)如图2,过点A作AN⊥BE于N,
∵F点为BE中点,BE=2BD,
∴BF=EF=BE=BD,
又∵∠EBD=90°,
∴∠BFD=∠BDF=45°,
∵△CBD∽△ABE,
∴AE=2CD=2,∠AEB=∠ADB=45°,
又∵∠BFD=∠AFE=45°,
∴∠AEF=∠AFE,
∴∠FAE=90°,AE=AF=2,
∴EF=2,
∵AN⊥BE,
∴AN=EN=FN=,
∵EF=BF=2,
∴BN=3,
∴AB===2.
26.证明:∵四边形ABCD是平行四边形,
∴AD=BC,AB∥CD,
∴∠DEA=∠BAF,
又∵∠AFB=∠D,
∴△ADE∽△BFA,
∴,
∴AE BF=AB AD=BC BA.
27.解:(1)如图,△A1B1C1为所求作的三角形,C1(3,3).
(2)如图所示,则△A2B2C2为所求作的三角形,B2(2,8).
28.解:(1)∵∠AED=∠B,∠DAE=∠CAB,
∴△AED∽△ABC,
∴∠ADF=∠C,
又∵,
∴△ADF∽△ACG;
(2)∵△ADF∽△ACG,
∴,
∵,
∴,
又∵AG=AF+FG,
∴.
29.解:(1)∵∠B=∠ADE=∠C,
∴∠BAD=180°﹣∠ADB﹣∠ADE,
∵∠CDE=180°﹣∠ADB﹣∠ADE,
∴∠BAD=∠CDE,
∴△BDA∽△CED;
(2)当AD=AE时,
∴∠1=∠AED,
∵∠1=45°,
∴∠1=∠ADE=45°,
∴∠DAE=90°,
∴点D与B重合,不合题意舍去;
当EA=ED时,如图1,
∴∠EAD=∠1=45°,
∵∠BAC=90°,
∴∠BAD=∠EAD=45°,
∴AD平分∠BAC,
∴AD垂直平分BC,
∴BD=3;
当DA=DE时,如图2,
∵∠1=∠C,∠DAE=∠CAD,
∴△ADE∽△ACD,
∴DA:AC=DE:DC,
∴AC=DC,
∵∠B=45°,
∴∠C=45°,∠BAC=90°,
∵BC=6,
∴,
∴,
综上所述,当△ADE是等腰三角形时,BD的长为3或.
30.(1)证明:在△OHN和△OGB中,∵∠OHN=∠OGB=90°,∠NOH=∠BOG,
∴△OHN∽△OGB,
∴∠ONH=∠B,
∵∠AOB=∠MON,
∴△OMN∽△OAB;
(2)解:由(1)得△OMN∽△OAB,
∵OM=3,OA=7,
∴.
31.解:(1)∵平行四边形ABCD,射线BE与CD的延长线交于点P,
∴AB∥CD,
∴∠ABF=∠P,
∵∠ABF=∠ACF,
∴∠ACF=∠P,
∵∠CEF=∠PEC,
∴△CEF∽△PEC,
∴,
即CE2=EF PE;
(2))∵平行四边形ABCD,射线BE与CD的延长线交于点P,
∴AB∥CD,AB=CD,AD∥BC,
∴∠ABF=∠P,
∵∠AEB=∠CEP,
∴△BEA∽△PEC,
∴,
∵点D是CP的中点,
∴CP=2CD=2AB,点F是BP的中点,
∴,
解得:PE=4,
∴PF=﹣BP
=(BE+PE)
=3,
∴EF=PE﹣PF=.
32.(1)证明:∵CD是角平分线,
∴∠ACD=∠DCE.
∵DE平分∠CDB,
∴∠CDE=∠EDB,
又∵DE∥AC,
∴∠A=∠EDB,
∴∠A=∠CDE,
∴△ACD∽△DCE,
∴,
∴CD2=CA CE;
(2)解:∵CE=2BE=2,
∴CE=2,BE=1,
∵CD平分∠CDB,
∴∠ACD=∠BCD,
又∵DE∥AC,
∴∠ACD=∠CDE,
∴∠BCD=∠CDE,
∴DE=CE=2,
∵DE∥AC,
∴,
∴CA=6,
∴CD2=CA CE=12,
∴.
33.解:(1)∵∠BAC=90°,AB=6,AC=8,
∴BC==10,
∵∠BAC=90°,AD⊥BC,
∴∠CAB=∠ADB,
∵∠B=∠B,
∴△CBA∽△ABD,
∴,
∴,
∴BD=3.6;
(2)证明:由(1)知:BD:AD=AB:AC①,
又∵E为AC的中点,AD⊥BC,
∴ED=AE=EC,
∴∠C=∠EDC=∠FAD=∠BDF,
又∵∠F为公共角,
∴△DBF∽△ADF,
∴BD:AD=DF:AF②,
由①②得,AB:AC=DF:AF,
∴AB AF=AC DF.
34.解:(1)∵DE∥AC,EF∥AB,
∴∠DEB=∠C,∠BDE=∠A,∠A=∠EFC.
∴∠BDE=∠EFC.
∴△BDE∽△EFC.
(2)∵DE∥AC,
∴∠A=∠EFC,∠B=∠FEC.
∴△ABC∽△FEC.
∵,
∴.
∴=.
∴.
∵△EFC的面积是25,
∴S△ABC=64.
35.解:(1)设经过x秒,△MCN的面积等于△ABC面积的.
×2x(8﹣x)=×8×10×.
解得x1=x2=4.
答:经过4秒后,△MCN的面积等于△ABC面积的;
(2)设经过t秒,△MCN与△ABC相似.
∵∠C=∠C,
∴可分为两种情况:
①=,即=,
解得t=;
②=,即=.
解得t=.
答:经过或秒,△MCN与△ABC相似.
36.(1)证明:∵四边形ABCD为菱形,
∴AB∥DG,
∴∠BAE=∠DGA,
又∠BAE=∠DAF,
∴∠DGA=∠DAF,
又∠ADF=∠GDA,
∴△ADF∽△GDA,
∴,
∴AD2=DF DG.
(2)解:∵AB∥GD,
∴,
∵AD∥BC,
∴,
∴,
即AH2=HG HE=(4+5)×4=36,
∴AH=6.
37.解:由已知得,AB=1m,CD=1.5m,AC=4m,FB=GD=1.5m,∠AOE=∠ABF=∠CDG=90°,∠BAF=∠OAE,∠DCG=∠OCE.
∵∠BAF=∠OAE,∠ABF=∠AOE,
∴△BAF∽△OAE,
∴=,即=,
∴OE=1.5OA,
∵∠DCG=∠OCE,∠CDG=∠COE,
∴△GDC∽△EOC,
∴=,即=,
∴OE=OA+4,
∴OE=1.5OA,
∴1.5OA=OA+4,
∴OA=8m,OE=12m.
答:教学楼的高度OE为12m.
一.选择题
1.下面四组线段中,成比例的是( )
A.a=2,b=3,c=4,d=5 B.a=1,b=2,c=2,d=4
C.a=4,b=6,c=8,d=10 D.a=,b=,c=3,d=
2.如果,那么的值等于( )
A. B. C. D.2
3.若(3b+d﹣2f≠0),则的值是( )
A.1 B. C.3 D.无法确定
4.如图,AB与CD相交于点E,点F在线段BC上,且AC∥EF∥DB.若BE=5,BF=3,AE=BC,则的值为( )
A. B. C. D.
5.如图,在△ABC中,D是BC上一点,连接AD,,F是AD的中点,连接BF并延长交AC于E,则的值是( )
A. B. C. D.
6.如图,在四边形ABCD中,已知∠ADC=∠BAC,那么补充下列条件后不能判定△ADC和△BAC相似的是( )
A.CA平分∠BCD B. C.AC2=BC CD D.∠DAC=∠ABC
7.如图,在△ACD中,AD=6,BC=5,AC2=AB(AB+BC),且△DAB∽△DCA,若AD=3AP,点Q是线段AB上的动点,则PQ的最小值是( )
A. B. C. D.
8.如图,BE与CD交于点A,∠C=∠E,AC=2,BC=4,AE=1.5,则DE=( )
A.2 B.3 C.3.5 D.4
9.如图,在△ABC中,点D是AB边上的一点.以B为圆心,以一定长度为半径画弧,分别交AB、BC于点F、G,以D为圆心,以相同的半径画弧,交AD于点M,以M为圆心,以FG的长度为半径画弧,交于点N,连接DN并延长交AC于点E.则下列式子中错误的是( )
A. B. C. D.
10.如图,在测量旗杆高度的数学活动中,某同学在脚下放了一面镜子,然后向后退,直到他刚好在镜子中看到旗杆的顶部.若眼睛距离地面AB=1.5m,同时量得BC=2m,CD=12m,则旗杆高度DE=( )
A.6m B.8m C.9m D.16m
11.如图,在△ABC中,CD,BE分别是△ABC的边AB,AC上的中线,则=( )
A. B. C. D.
12.如图所示是利用图形的位似绘制的一幅“小鱼”图案,其中O为位似中心,且OA=2OD,若图案中鱼身(△ABC)的面积为S,则鱼尾(△DEF)的面积为( )
A. B.S C.S D.S
13.如图,已知点C,D都是线段AB的黄金分割点,如果CD=4,那么AB的长度是( )
A.2﹣2 B.6﹣2 C.8+4 D.2+
二.填空题
14.已知(abc≠0,a+b≠c),则= .
15.若===k成立,则k的值为 .
16.若(k≠0),则y=kx+k﹣2一定经过第 象限.
17.如图,点D、E分别在△ABC的边AB,AC上,DE∥BC,点G在边BC上,AG交DE于点H,点O是线段AG的中点,若AD:DB=3:1,则AO:OH= .
18.如图,在△ABC中,AB=5,AC=4,若进行以下操作,在边BC上从左到右依次取点D1、D2、D3、D4、…;过点D1作AB、AC的平行线分别交AC、AB于点E1、F1;过点D2作AB、AC的平行线分别交AC、AB于点E2、F2;过点D3作AB、AC的平行线分别交AC、AB于点E3、F3…,则4(D1E1+D2E2+…+D2021E2021)+5(D1F1+D2F2+…+D2021F2021)= .
19.如图,一组平行线l1、l2、l3相交于直线l4、l5,则= .
20.如图所示的正方形网格中,每个小正方形的边长均为1,四边形ABCD的面积是 .若四边形EFGH与四边形ABCD相似,则四边形EFGH的面积是 .
21.在△ABC中,AB=6cm,AC=9cm,动点D从点B开始沿BA边运动,速度为1cm/s;动点E从点A开始沿AC边运动,速度为2cm/s.如果D,E两动点同时运动,那么当它们运动 s时,由D,A,E三点连成的三角形与△ABC相似.
22.如图,在△ABC中,AB=6,BC=8,AC=7,点D,E分别在AB,BC上,将△BDE沿ED折叠,点B的对应点F刚好落在AC上.当△CEF与△ABC相似时,BE的长为 .
23.如图,菱形ABCD中,对角线AC与BD相交于点O.将线段AB绕点B顺时针方向旋转,使点A落在BD上的点H.点E为边BC的中点,连接HE,交AC于点P,若AC=12,BD=16,则线段PC的长为 .
24.△AOB三个顶点的坐标分别为A(5,0),O(0,0),B(3,6),以原点O为位似中心,相似比为,将△AOB缩小,则点B的对应点B′的坐标是 .
三.解答题
25.如图1,Rt△ABC中,∠ABC=90°,AB=2BC,D为AC边上一点,BE⊥BD,BE=2BD,连接DE交AB于F点.
(1)求证:△CBD∽△ABE;
(2)若∠DBC=30°,求的值;
(3)如图2,若D在射线AC上,且CD=1,当F点为BE中点时,求AB的值
.
26.如图,在 ABCD中,点E为CD上一点,连接AE,在AE上取一点F,使得∠AFB=∠D.求证:AE BF=BC BA.
27.如图,在平面直角坐标系中,已知△ABC三个顶点的坐标分别为A(﹣1,2),B(﹣3,4),C(﹣2,6).
(1)画出△ABC绕点A顺时针旋转90°后得到的△A1B1C1,写出点C1的坐标.
(2)以原点O为位似中心,画出将△A1B1C1三条边放大为原来的2倍后得△A2B2C2,写出点B2的坐标.
28.如图,在△ABC中,点D、E分别在边AB,AC上,∠AED=∠B,线段AG分别交线段DE,BC于点F,G,且.
(1)求证:△ADF∽△ACG;
(2)若=,求的值.
29.如图,在△ABC中,点D、E分别在边BC、AC上,连接AD、DE.且∠B=∠ADE=∠C.
(1)证明:△BDA∽△CED;
(2)若∠B=45°,BC=6,当点D在BC上运动时(点D不与B、C重合).且△ADE是等腰三角形,求此时BD的长.
30.如图在锐角三角形OAB中,点M,N分别在边OB,OA上,OG⊥AB于点G,OH⊥MN于点H,∠NOH=∠GOB.
(1)求证:△OMN∽△OAB;
(2)若OM=3,OA=7,求的值.
31.如图,在平行四边形ABCD中,点E是AC上一点,射线BE与CD的延长线交于点P,与边AD交于点F,连接FC.
(1)若∠ABF=∠ACF,求证:CE2=EF EP;
(2)若点D是CP中点,BE=2,求EF的长.
32.如图,在△ABC中,CD是角平分线,DE平分∠CDB交BC于点E,且DE∥AC.
(1)求证:CD2=CA CE.
(2)若CE=2BE=2,求CD的长.
33.已知:如图,在Rt△ABC中,∠BAC=90°,AD⊥BC于D,E为直角边AC的中点,过D,E作直线交AB的延长线于F.
(1)若AB=6,AC=8,求BD长;
(2)求证:AB AF=AC DF.
34.如图,在△ABC中,点D,E,F分别在AB,BC,AC边上,DE∥AC,EF∥AB.
(1)求证:△BDE∽△EFC.
(2)若,△EFC的面积是25,求△ABC的面积.
35.如图,在Rt△ABC中,∠C=90°,AC=10cm,BC=8cm.点M从点C出发,以2cm/s的速度沿CA向点A匀速运动,点N从点B出发,以1cm/s的速度沿BC向点C匀速运动,当一个点到达终点时,另一点也随即停止运动.
(1)经过几秒后,△MCN的面积等于△ABC面积的?
(2)经过几秒,△MCN与△ABC相似?
36.如图,在菱形ABCD中,点E,F分别在边BC,DC上,AE与BD交于点H,AE的延长线与DC的延长线交于点G,∠BAE=∠DAF.
(1)求证:AD2=DF DG;
(2)若HE=4,EG=5,求AH的长.
37.如图,小明同学为了测量教学楼的高度OE,先在操场上点A处放一面镜子,从点A处后退1m到点B处,恰好在镜子中看到楼的顶部E点;再将镜子向后移动4m放在C处,从点C处向后退1.5m到点D处,恰好再次在镜子中看到楼的顶部E点,测得小明的眼睛距地面的高度FB,GD为1.5m,点O,A,B,C,D在同一水平线上,镜子可看成一个点.求教学楼的高度OE.
参考答案
1.解:A、2×5≠3×4,故选项不符合题意;
B、1×4=2×2,故选项符合题意;
C、4×10≠5×6,故选项不符合题意;
D、×3≠×,故选项不符合题意.
故选:B.
2.解:∵,
∴3(a﹣b)=a,
∴a=b,
∴==.
故选:B.
3.解:∵(3b+d﹣2f≠0),
∴a=3b,c=3d,e=3f,
∴===3.
故选:C.
4.解:设CF=x,
∵EF∥AC,
∴=,
∴=,
解得x=,
∴CF=,
∵EF∥DB,
∴===.
故选:A.
5.解:过D点作DH∥BE交AC于H,如图,
∵F点为AD的中点,
∴AF=FD,
∵FE∥DH,
∴==1,即AE=EH,
∵DH∥BE,
∴==,CH=3EH,
∴=.
故选:A.
6.解:在△ADC和△BAC中,∠ADC=∠BAC,
如果△ADC∽△BAC,需满足的条件有:
①∠DAC=∠ABC或AC是∠BCD的平分线;
②=;
故选:C.
7.解:∵△DAB∽△DCA,
∴,
∴,
解得:BD=4(负值舍去),
∵△DAB∽△DCA,
∴,
∴AC=,
∵AC2=AB(AB+BC),
∴(AB)2=AB(AB+BC),
∴AB=4,
∴AB=BD=4,
过B作BH⊥AD于H,
∴AH=AD=3,
∴BH===,
∵AD=3AP,AD=6,
∴AP=2,
当PQ⊥AB时,PQ的值最小,
∵∠AQP=∠AHB=90°,∠PAQ=∠BAH,
∴△APQ∽△ABH,
∴,
∴=,
∴PQ=,
故选:A.
8.解:∵∠C=∠E,∠CAB=∠DAE,
∴△CAB∽△EAD,
∴,
∴,
∴DE=3,
故选:B.
9.解:由题意可得:∠ABC=∠ADE,
∴DE∥BC,
∴,,,故选项A,B,D不合题意,
∵DE∥BC,
∴△ADE∽△ABC,
∴,故选项C符合题意,
故选:C.
10.解:∵AB⊥BD,DE⊥BD,
∴∠ABC=∠EDC=90°,
∵∠ACB=∠DCE,
∴△ABC∽△EDC,
∴=,
∴=,
∴DE=9(m),
故选:C.
11.解:∵CD,BE分别是△ABC的边AB,AC上中线,
∴D是AB的中点,E是AC的中点,
∴DE是△ABC的中位线,
∴DE∥BC,DE=BC,
∴△DEF∽△CBF,
∴==,
故选:D.
12.解:∵△ABC与△DEF是以O为位似中心位似图形,OA=2OD,
∴△ABC∽△DEF,且相似比为2,
∴=22=4,
∵△ABC的面积为S,
∴△DEF的面积S,
故选:C.
13.解:∵点C,D都是线段AB的黄金分割点,
∴AD=AB,BC=AB,
∵CD=4,AD+BC﹣CD=AB,
∴AB+AB﹣4=AB,
解得:AB=8+4,
故选:C.
14.解:设=k,
则a=2k,b=3k,c=4k,
所以
=
=
=3,
故答案为:3.
15.解:当a+b+c≠0时,根据比例的等比性质,得k==1:
当a+b+c=0时,即a+b=﹣c,则k==﹣2.
故答案为:1或﹣2.
16.解:根据比例的等比性质,得k=,
当a+b+c≠0时,k=2,
∴直线解析式是y=2x,
∴图象经过一、三象限.
当a+b+c=0时,a+b=﹣c,
∴k===﹣1,
∴直线解析式是y=﹣x﹣3,
∴图象经过二、三、四象限.
综上所述,直线一定经过第三象限,
故答案为:三.
17.解:∵点O是线段AG的中点,
∴OA=OG=AG,
∵DE∥BC,AD:DB=3:1,
∴===,==,
∴OH=OG﹣HG=AG﹣AG=AG,
∴AO:OH=(AG):(AG)=2:1,
故答案为:2:1.
18.解:∵D1F1∥AC,
∴.
∵D1F1∥AC,D1E1∥AB,
∴四边形D1E1AF1为平行四边形.
∴D1E1=AF1.
∴BF1=AB﹣AF1=AB﹣D1E1.
∴.
将AB=5,AC=4代入上式得:4D1E1+5D1F1=20.
同理可得:4D2E2+5D2F2=20,
…
4D2021E2021+5D2021F2021=20,
∴4(D1E1+D2E2+…+D2021E2021)+5(D1F1+D2F2+…+D2021F2021)
=4D1E1+5D1F1+4D2E2+5D2F2+…+4D2021E2021+5D2021F2021
=20+20+…+20
=2021×20
=40420.
故答案为40420.
19.解:∵l1∥l2,
∴=①,
∵l2∥l3,
∴=②,
①×②,得=,
故答案为:.
20.解:∵S四边形ABCD=2×4﹣×1×2﹣×1×2﹣1×1﹣×1×1=.
又∵四边形EFGH与四边形ABCD相似,
∴S四边形EFGH:S四边形ABCD=()2=()2=,
∴S四边形EFGH=×=.
故答案为:,.
21.解:根据题意得:AE=2t,BD=t,
∴AD=6﹣t,
∵∠A=∠A,
∴分两种情况:
①当=时,
即=,解得:t=;
②当=时,
即=,解得:t=;
综上所述:当t=或时,△ADE与△ABC相似.
22.解:∵将△BDE沿DE翻折得到△FDE,
∴BE=EF,
∵BC=8,
∴CE=8﹣BE,
当△CEF与△ABC相似时,=或=,即=或=,
解得:BE=或,
故答案是:或.
23.解:过E点作EF⊥BD于F,
∵四边形ABCD是菱形,
∴AC⊥BD,
∴EF∥AC,
∵AC=12,BD=16,
∴OC=OA=AC=6,OB=OD=BD=8,
∴BC===10,
∴BH=AB=BC=10,
∴OH=BH﹣OB=2,
∵E是BC的中点,EF∥AC,
∴EF=OC=3,OF=OB=4,
∴HF=OH+OF=6,
∵EF∥AC,
∴△HOP∽△HFE,
∴,
∴,
∴OP=1,
∴CP=OC﹣OP=5.
故答案为:5.
24.解:∵△AOB顶点B的坐标为(3,6),以原点O为位似中心,相似比为,将△AOB缩小,
∴点B的对应点B′的坐标为(3×,6×)或(3×(﹣),6×(﹣)),即(2,4)或(﹣2,﹣4),
故答案为:(2,4)或(﹣2,﹣4).
25.解:(1)∵BE⊥BD,
∴∠DBE=90°=∠ABC,
∴∠CBD=∠ABE,
∵AB=2BC,BE=2BD,
∴=,
∴△CBD∽△ABE;
(2)如图1,过点D作DH⊥BC于H,
∵∠ABC=90°,AB=2BC,
∴AC==BC,
∵△CBD∽△ABE,
∴,∠AEB=∠BDC,
∴AE=2CD,
∵DH⊥BC,
∴∠ABC=∠DHC=90°,
又∵∠C=∠C,
∴△ABC∽△DHC,
∴,
∴CH=CD,DH=CD,
∵∠DBC=30°,
∴BD=2DH=CD,
∵∠AEB=∠BDC,∠BDC+∠ADB=180°,
∴∠AEB+∠ADB=180°,
∴点A,点E,点B,点D四点共圆,
∴∠AED=∠ABD,∠BAE=∠BDE,
∴△AEF∽△DBF,
∴,
∴;
(3)如图2,过点A作AN⊥BE于N,
∵F点为BE中点,BE=2BD,
∴BF=EF=BE=BD,
又∵∠EBD=90°,
∴∠BFD=∠BDF=45°,
∵△CBD∽△ABE,
∴AE=2CD=2,∠AEB=∠ADB=45°,
又∵∠BFD=∠AFE=45°,
∴∠AEF=∠AFE,
∴∠FAE=90°,AE=AF=2,
∴EF=2,
∵AN⊥BE,
∴AN=EN=FN=,
∵EF=BF=2,
∴BN=3,
∴AB===2.
26.证明:∵四边形ABCD是平行四边形,
∴AD=BC,AB∥CD,
∴∠DEA=∠BAF,
又∵∠AFB=∠D,
∴△ADE∽△BFA,
∴,
∴AE BF=AB AD=BC BA.
27.解:(1)如图,△A1B1C1为所求作的三角形,C1(3,3).
(2)如图所示,则△A2B2C2为所求作的三角形,B2(2,8).
28.解:(1)∵∠AED=∠B,∠DAE=∠CAB,
∴△AED∽△ABC,
∴∠ADF=∠C,
又∵,
∴△ADF∽△ACG;
(2)∵△ADF∽△ACG,
∴,
∵,
∴,
又∵AG=AF+FG,
∴.
29.解:(1)∵∠B=∠ADE=∠C,
∴∠BAD=180°﹣∠ADB﹣∠ADE,
∵∠CDE=180°﹣∠ADB﹣∠ADE,
∴∠BAD=∠CDE,
∴△BDA∽△CED;
(2)当AD=AE时,
∴∠1=∠AED,
∵∠1=45°,
∴∠1=∠ADE=45°,
∴∠DAE=90°,
∴点D与B重合,不合题意舍去;
当EA=ED时,如图1,
∴∠EAD=∠1=45°,
∵∠BAC=90°,
∴∠BAD=∠EAD=45°,
∴AD平分∠BAC,
∴AD垂直平分BC,
∴BD=3;
当DA=DE时,如图2,
∵∠1=∠C,∠DAE=∠CAD,
∴△ADE∽△ACD,
∴DA:AC=DE:DC,
∴AC=DC,
∵∠B=45°,
∴∠C=45°,∠BAC=90°,
∵BC=6,
∴,
∴,
综上所述,当△ADE是等腰三角形时,BD的长为3或.
30.(1)证明:在△OHN和△OGB中,∵∠OHN=∠OGB=90°,∠NOH=∠BOG,
∴△OHN∽△OGB,
∴∠ONH=∠B,
∵∠AOB=∠MON,
∴△OMN∽△OAB;
(2)解:由(1)得△OMN∽△OAB,
∵OM=3,OA=7,
∴.
31.解:(1)∵平行四边形ABCD,射线BE与CD的延长线交于点P,
∴AB∥CD,
∴∠ABF=∠P,
∵∠ABF=∠ACF,
∴∠ACF=∠P,
∵∠CEF=∠PEC,
∴△CEF∽△PEC,
∴,
即CE2=EF PE;
(2))∵平行四边形ABCD,射线BE与CD的延长线交于点P,
∴AB∥CD,AB=CD,AD∥BC,
∴∠ABF=∠P,
∵∠AEB=∠CEP,
∴△BEA∽△PEC,
∴,
∵点D是CP的中点,
∴CP=2CD=2AB,点F是BP的中点,
∴,
解得:PE=4,
∴PF=﹣BP
=(BE+PE)
=3,
∴EF=PE﹣PF=.
32.(1)证明:∵CD是角平分线,
∴∠ACD=∠DCE.
∵DE平分∠CDB,
∴∠CDE=∠EDB,
又∵DE∥AC,
∴∠A=∠EDB,
∴∠A=∠CDE,
∴△ACD∽△DCE,
∴,
∴CD2=CA CE;
(2)解:∵CE=2BE=2,
∴CE=2,BE=1,
∵CD平分∠CDB,
∴∠ACD=∠BCD,
又∵DE∥AC,
∴∠ACD=∠CDE,
∴∠BCD=∠CDE,
∴DE=CE=2,
∵DE∥AC,
∴,
∴CA=6,
∴CD2=CA CE=12,
∴.
33.解:(1)∵∠BAC=90°,AB=6,AC=8,
∴BC==10,
∵∠BAC=90°,AD⊥BC,
∴∠CAB=∠ADB,
∵∠B=∠B,
∴△CBA∽△ABD,
∴,
∴,
∴BD=3.6;
(2)证明:由(1)知:BD:AD=AB:AC①,
又∵E为AC的中点,AD⊥BC,
∴ED=AE=EC,
∴∠C=∠EDC=∠FAD=∠BDF,
又∵∠F为公共角,
∴△DBF∽△ADF,
∴BD:AD=DF:AF②,
由①②得,AB:AC=DF:AF,
∴AB AF=AC DF.
34.解:(1)∵DE∥AC,EF∥AB,
∴∠DEB=∠C,∠BDE=∠A,∠A=∠EFC.
∴∠BDE=∠EFC.
∴△BDE∽△EFC.
(2)∵DE∥AC,
∴∠A=∠EFC,∠B=∠FEC.
∴△ABC∽△FEC.
∵,
∴.
∴=.
∴.
∵△EFC的面积是25,
∴S△ABC=64.
35.解:(1)设经过x秒,△MCN的面积等于△ABC面积的.
×2x(8﹣x)=×8×10×.
解得x1=x2=4.
答:经过4秒后,△MCN的面积等于△ABC面积的;
(2)设经过t秒,△MCN与△ABC相似.
∵∠C=∠C,
∴可分为两种情况:
①=,即=,
解得t=;
②=,即=.
解得t=.
答:经过或秒,△MCN与△ABC相似.
36.(1)证明:∵四边形ABCD为菱形,
∴AB∥DG,
∴∠BAE=∠DGA,
又∠BAE=∠DAF,
∴∠DGA=∠DAF,
又∠ADF=∠GDA,
∴△ADF∽△GDA,
∴,
∴AD2=DF DG.
(2)解:∵AB∥GD,
∴,
∵AD∥BC,
∴,
∴,
即AH2=HG HE=(4+5)×4=36,
∴AH=6.
37.解:由已知得,AB=1m,CD=1.5m,AC=4m,FB=GD=1.5m,∠AOE=∠ABF=∠CDG=90°,∠BAF=∠OAE,∠DCG=∠OCE.
∵∠BAF=∠OAE,∠ABF=∠AOE,
∴△BAF∽△OAE,
∴=,即=,
∴OE=1.5OA,
∵∠DCG=∠OCE,∠CDG=∠COE,
∴△GDC∽△EOC,
∴=,即=,
∴OE=OA+4,
∴OE=1.5OA,
∴1.5OA=OA+4,
∴OA=8m,OE=12m.
答:教学楼的高度OE为12m.
同课章节目录
- 第23章 数据分析
- 23.1 平均数与加权平均数
- 23.2 中位数与众数
- 23.3 方差
- 23.4 用样本估计总体
- 第24章 一元二次方程
- 24.1 一元二次方程
- 24.2 解一元二次方程
- 24.3 一元二次方程根与系数的关系
- 24.4 一元二次方程的应用
- 第25章 图形的相似
- 25.1 比例线段
- 25.2 平行线分线段成比例
- 25.3 相似三角形
- 25.4 相似三角形的判定
- 25.5 相似三角形的性质
- 25.6 相似三角形的应用
- 25.7 相似多边形和图形的位似
- 第26章 解直角三角形
- 26.1 锐角三角函数
- 26.2 锐角三角函数的计算
- 26.3 解直角三角形
- 26.4 解直角三角形的应用
- 第27章 反比例函数
- 27.1 反比例函数
- 27.2 反比例函数的图像和性质
- 27.3 反比例函数的应用
- 第28章 圆
- 28.1 圆的概念和性质
- 28.2 过三点的圆
- 28.3 圆心角和圆周角
- 28.4 垂径定理
- 28.5 弧长和扇形面积
