冀教版 2021-2022学年九年级数学上册25.2平行线分线段成比例 同步达标测评(word版含解析)
文档属性
| 名称 | 冀教版 2021-2022学年九年级数学上册25.2平行线分线段成比例 同步达标测评(word版含解析) |

|
|
| 格式 | doc | ||
| 文件大小 | 422.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 冀教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-10-19 17:31:11 | ||
图片预览



文档简介
2021-2022学年冀教版九年级数学上册《25.2平行线分线段成比例》同步达标测评(附答案)
一.选择题(共10小题,满分50分)
1.如图,l1∥l2∥l3,直线a,b与l1、l2、l3分别相交于A、B、C和点D、E、F.若=,DE=4,则EF的长是( )
A. B. C.6 D.10
2.在△ABC中,AD:BD=1:1,AE:CE=1:2,BE与CD交于点P,则BP:PE=( )
A.2:1 B.1:2 C.2:3 D.3:2
3.如图,在Rt△ABC中,∠C=90°,AC=BC=6cm,点P从点A出发,沿AB方向以每秒cm的速度向终点B运动;同时,动点Q从点B出发沿BC方向以每秒1cm的速度向终点C运动,将△PQC沿BC翻折,点P的对应点为点P′.设点Q运动的时间为t秒,若四边形QPCP′为菱形,则t的值为( )
A. B.2 C. D.3
4.如图,在平行四边形ABCD中,E为AB的中点,F为AD上一点,EF交AC于G,AF=2cm,DF=4cm,AG=3cm,则AC的长为( )
A.9cm B.14cm C.15cm D.18cm
5.如图,利用标杆BE测量建筑物DC的高度,如果标杆BE长为1.5米,测得AB=2米,BC=10米.则楼高CD是( )
A.8米 B.7.5米 C.9.5米 D.9米
6.如图,在平行四边形ABCD中,E是AD上一点,连接CE并延长交BA的延长线于点F,则下列结论中错误的是( )
A.∠AEF=∠DEC B.FA:CD=AE:BC
C.FA:AB=FE:EC D.AB=DC
7.△ABC中,D、E分别是边AB、AC上的点,且DE∥BC,已知,那么等于( )
A. B. C. D.
8.已知线段a、b,求作线段x,使,正确的作法是( )
A. B.
C. D.
9.如图,在△ABC中,D、E分别是AB、AC上一点,下面有四个条件:
(1);(2);(3);(4).
其中一定能判定DE∥BC有( )
A.1个 B.2个 C.3个 D.4个
10.如图,在△ABC中,AD是BC边上的中线,E在AC边上,且AE:EC=1:2,BE交AD于P,则AP:PD等于( )
A.1:1 B.1:2 C.2:3 D.4:3
二.填空题(共5小题,满分30分)
11.如图,点A1,A2,A3,A4在射线OA上,点B1,B2,B3在射线OB上,且A1B1∥A2B2∥A3B3,A2B1∥A3B2∥A4B3.若△A2B1B2,△A3B2B3的面积分别为1,9,则图中三个阴影三角形面积之和为 .
12.如图,△ABC的面积是63,D是BC上的一点,且BD:CD=2:1,DE∥AC交AB于E,延长DE到F,使FE:ED=2:1,则△CDF的面积是 .
13.如图,已知:△ABC中,DE∥BC,AD=3,DB=6,AE=2,则EC= .
14.如图,已知点O是△ABC中BC边上的中点,且,则= .
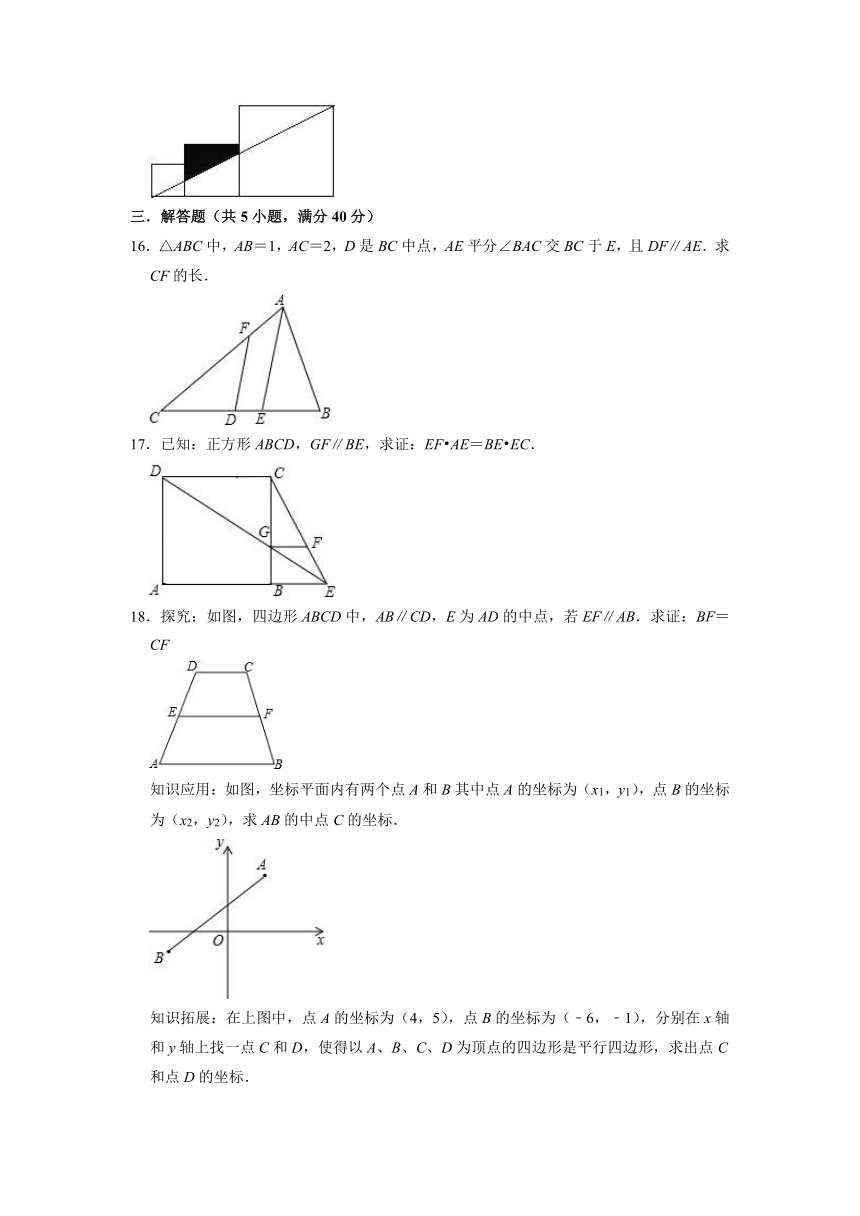
15.将边长分别为2、3、5的三个正方形按图所示的方式排列,则图中阴影部分的面积为 .
三.解答题(共5小题,满分40分)
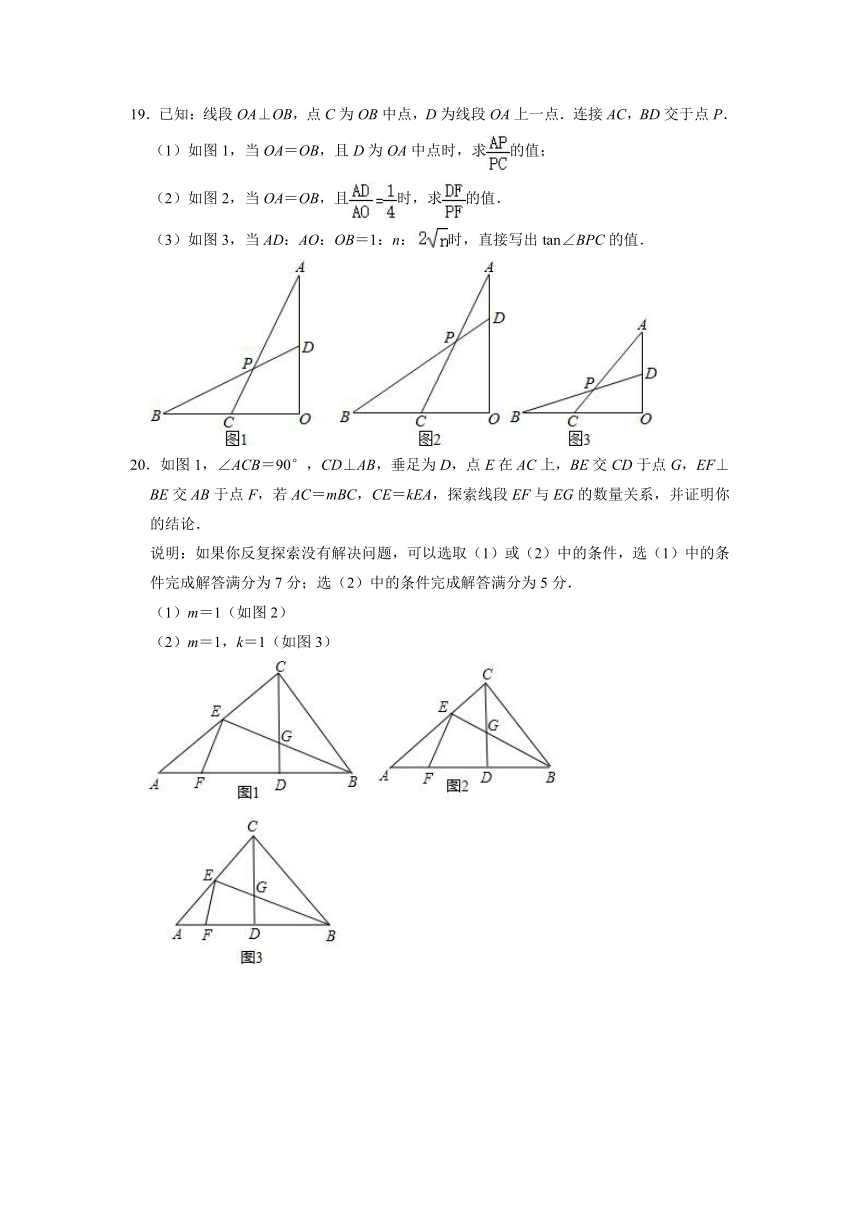
16.△ABC中,AB=1,AC=2,D是BC中点,AE平分∠BAC交BC于E,且DF∥AE.求CF的长.
17.已知:正方形ABCD,GF∥BE,求证:EF AE=BE EC.
18.探究:如图,四边形ABCD中,AB∥CD,E为AD的中点,若EF∥AB.求证:BF=CF
知识应用:如图,坐标平面内有两个点A和B其中点A的坐标为(x1,y1),点B的坐标为(x2,y2),求AB的中点C的坐标.
知识拓展:在上图中,点A的坐标为(4,5),点B的坐标为(﹣6,﹣1),分别在x轴和y轴上找一点C和D,使得以A、B、C、D为顶点的四边形是平行四边形,求出点C和点D的坐标.
19.已知:线段OA⊥OB,点C为OB中点,D为线段OA上一点.连接AC,BD交于点P.
(1)如图1,当OA=OB,且D为OA中点时,求的值;
(2)如图2,当OA=OB,且时,求的值.
(3)如图3,当AD:AO:OB=1:n:时,直接写出tan∠BPC的值.
20.如图1,∠ACB=90°,CD⊥AB,垂足为D,点E在AC上,BE交CD于点G,EF⊥BE交AB于点F,若AC=mBC,CE=kEA,探索线段EF与EG的数量关系,并证明你的结论.
说明:如果你反复探索没有解决问题,可以选取(1)或(2)中的条件,选(1)中的条件完成解答满分为7分;选(2)中的条件完成解答满分为5分.
(1)m=1(如图2)
(2)m=1,k=1(如图3)
参考答案
一.选择题(共10小题,满分50分)
1.解:∵l1∥l2∥l3,
∴,
即,
解得:EF=6.
故选:C.
2.解:
过B作BM∥DC交AC的延长线于M,
∵DC∥BM,
∴=,
∵AD:BD=1:1,
∴AC=CM,
∵AE:CE=1:2,
∴=,
∵DC∥BM,
∴==,
故选:D.
3.解:连接PP′交BC于O,
∵若四边形QPCP′为菱形,
∴PP′⊥QC,
∴∠POQ=90°,
∵∠ACB=90°,
∴PO∥AC,
∴=,
∵设点Q运动的时间为t秒,
∴AP=t,QB=t,
∴QC=6﹣t,
∴CO=3﹣,
∵AC=CB=6,∠ACB=90°,
∴AB=6,
∴=,
解得:t=2,
故选:B.
4.解:∵四边形ABCD是平行四边形,
∴BC=AD=6cm,BC∥AD.
∴∠EAF=∠EBH,∠AFE=∠BHE,
又AE=BE,
∴△AFE≌△BHE,
∴BH=AF=2cm.
∵BC∥AD,
∴,
即,
则CG=12,
则AC=AG+CG=15(cm).
故选:C.
5.解:由题意可得,BE∥CD,
所以,即,
解得CD=9米,故选D.
6.解:A、根据对顶角相等,此结论正确;
B、根据平行线分线段成比例定理,得FA:FB=AE:BC,所以此结论错误;
C、根据平行线分线段成比例定理得,此项正确;
D、根据平行四边形的对边相等,所以此项正确.
故选:B.
7.解:∵DE∥BC,
∴,
又∵,
∴,
∴=.故选:D.
8.解:由题意,
∴,
∵线段x没法先作出,
∴B选项错误,
根据平行线分线段成比例定理,只有C符合.
故选:C.
9.解:根据对应线段成比例两直线平行,
有,
得到(1)(2)(3)正确,(4)的线段不对应(如图所示)DE′=DE时,DE′不平行于BC,所以不正确.故选:C.
10.解:过点D作DF∥BE,交AC于F,
∴AD是BC边上的中线,
即BD=CD,
∴EF=CF,
∵AE:EC=1:2,
∴AE=EF=FC,
∴AE:EF=1:1,
∴AP:PD=AE:EF=1:1.故选:A.
二.填空题(共5小题,满分30分)
11.解:△A2B1B2,△A3B2B3的面积分别为1,9,
又∵A2B2∥A3B3,A2B1∥A3B2,
∴∠OB2A2=∠OB3A3,∠A2B1B2=∠A3B2B3,
∴△B1B2A2∽△B2B3A3,
==,
∴=.
∵=,△A3B2B3的面积是9,
∴△A2B2A3的面积为=×S△A3B2B3=×9=3(等高的三角形的面积的比等于底边的比).
同理可得:△A3B3A4=3×S△A3B2B3=3×9=27;
△A1B1A2的面积=S△A2B1B2=×1=.
故三个阴影面积之和=+3+27=30.
故答案为:30.
12.方法一:
解:连接CE,因为BD:CD=2:1,所以△BDE和△CDE的面积之比为2:1,
又因为DE∥AC,
∴=,
∴S△BDE:S△ABC=4:9,
又因为△ABC的面积是63,
∴△BDE的面积为:28,
所以△CDE的面积为14,
因为FE:ED=2:1,所以△FDC和△CDE的面积之比为3:1
故答案为:42.
方法二:解:作MW⊥BC,AN⊥BC,垂足分别为W,N.
∵BD:CD=2:1,DE∥AC,
∴BE:AE=2:1,
∴BD:BC=DE:AC=BE:AB=2:3,
∴S△BDE:S△ABC=4:9,
∴S△BDE=×63=28,
∵FE:ED=2:1=4:2,
∴EF:AC=4:3,
∴S△MEF:S△AMC=16:9,
∴EM:AM=4:3,
假设EM=4x,AM=3x,BE=AB=2AE=2(EM+AM)=14x,
∴BM:AM=18x:3x=18:3,
∴MW:AN=BM:AB=18:21=6:7,
∴S△BMC:S△ABC=BC WM:BC AN=WM:AN=6:7,
∵S△ABC=63,
∴S△BMC=54,
∴S△AMC=63﹣54=9,
∵S△MEF:S△AMC=16:9,
∴S△MEF=16,
∵S△BDE=×63=28,
∴S四边形MEDC=63﹣9﹣28=26,
∴△CDF的面积是:26+16=42.
故答案为:42.
13.解:∵△ABC中,DE∥BC,
∴,
∵AD=3,DB=6,AE=2,
∴,
∴EC=4.
故答案为:4.
14.解:过B作BF∥AC,交DE于点F,
∵BF∥AC,
∴∠FBO=∠C,∠BFO=∠CEO,
又O为BC的中点,∴BO=CO,
在△OBF和△OCE中,
,
∴△OBF≌△OCE(AAS),
∴BF=CE,
∵=,∴=,
又∵BF∥AE,∴==,
∴=,
则==.
故答案为:.
15.解:∵VB∥ED,三个正方形的边长分别为2、3、5,
∴VB:DE=AB:AD,即VB:5=2:(2+3+5)=1:5,
∴VB=1,
∵CF∥ED,
∴CF:DE=AC:AD,即CF:5=5:10
∴CF=2.5,
∵S梯形VBFC=(BV+CF) BC=,
∴阴影部分的面积=S正方形BCQW﹣S梯形VBCF=.
故答案为:
三.解答题(共5小题,满分40分)
16.解:分别过E作EH⊥AB于H,EG⊥AC于G,因AE平分∠BAC,所以有EH=EG.
从而有.
又由DF∥AE,得
所以CF=CA==.
17.证明:∵四边形ABCD是正方形,
∴AB∥CD,AD∥BC,
∵GF∥BE,
∴GF∥CD,
∴,
同理:,
∴,
∴EF AE=BE EC.
18.【探究】证明:过点F作GH∥AD,交AB于H,交DC的延长线于点G,
∵AH∥EF∥DG,AD∥GH,
∴四边形AHFE和四边形DEFG都是平行四边形,
∴FH=AE,FG=DE,
∵AE=DE,
∴FG=FH,
∵AB∥DG,
∴∠G=∠FHB,∠GCF=∠B,
∴△CFG≌△BFH,
∴FC=FB;
【知识应用】过点C作CM⊥x轴于点M,过点A作AN⊥x轴于点N,过点B作BP⊥x轴于点P,
则点P的坐标为(x2,0),点N的坐标为(x1,0),
由探究的结论可知,MN=MP,
∴点M的坐标为(,0),
∴点C的横坐标为,
同理可求点C的纵坐标为,
∴点C的坐标为(,).
【知识拓展】
①当AB是平行四边形一条边,且点C在x轴的正半轴时,AD与BC互相平分,
设点C的坐标为(a,0),点D的坐标为(0,b)
由上面的结论可知:﹣6+a=4+0,﹣1+0=5+b,
∴a=10,b=﹣6,
∴此时点C的坐标为(10,0),点D的坐标为(0,﹣6),
②同理,当AB是平行四边形一条边,且点C在x轴的负半轴时,求得点C的坐标为(﹣10,0),点D的坐标为(0,6),
③当AB是对角线时点C的坐标为(﹣2,0),点D的坐标为(0,4).
19.
解:(1)过D作DE∥CO交AC于E,
∵D为OA中点,
∴AE=CE=,,
∵点C为OB中点,
∴BC=CO,,
∴,
∴PC==,
∴=2;
(2)过点D作DE∥BO交AC于E,
∵,
∴==,
∵点C为OB中点,
∴,
∴,
∴PC==,
过D作DF⊥AC,垂足为F,设AD=a,则AO=4a,
∵OA=OB,点C为OB中点,
∴CO=2a,
在Rt△ACO中,AC===2a,
又∵Rt△ADF∽Rt△ACO,
∴,
∴AF=,DF=,
PF=AC﹣AF﹣PC=2a﹣﹣=,
=.
(3)与(2)的方法相同,设AD=a,求出DF=a,
PF=a,所以tan∠BPC=.
20.解:过E作EM⊥AB,EN⊥CD,
∵CD⊥AB,∴EM∥CD,EN∥AB,
∵EF⊥BE,∴∠EFM+∠EBF=90°,
∵∠EBF+∠DGB=90°,∠DGB=∠EGN(对顶角相等)
∴∠EFM=∠EGN,
∴,
在△ADC中,
∵EM∥CD,
∴,
又CE=kEA,
∴AC=(k+1)AE
∴CD=(k+1)EM,
同理,
∴AD=EN,
∵∠ACB=90°,CD⊥AB,AC=mBC
∴,
∴EF=EG.
一.选择题(共10小题,满分50分)
1.如图,l1∥l2∥l3,直线a,b与l1、l2、l3分别相交于A、B、C和点D、E、F.若=,DE=4,则EF的长是( )
A. B. C.6 D.10
2.在△ABC中,AD:BD=1:1,AE:CE=1:2,BE与CD交于点P,则BP:PE=( )
A.2:1 B.1:2 C.2:3 D.3:2
3.如图,在Rt△ABC中,∠C=90°,AC=BC=6cm,点P从点A出发,沿AB方向以每秒cm的速度向终点B运动;同时,动点Q从点B出发沿BC方向以每秒1cm的速度向终点C运动,将△PQC沿BC翻折,点P的对应点为点P′.设点Q运动的时间为t秒,若四边形QPCP′为菱形,则t的值为( )
A. B.2 C. D.3
4.如图,在平行四边形ABCD中,E为AB的中点,F为AD上一点,EF交AC于G,AF=2cm,DF=4cm,AG=3cm,则AC的长为( )
A.9cm B.14cm C.15cm D.18cm
5.如图,利用标杆BE测量建筑物DC的高度,如果标杆BE长为1.5米,测得AB=2米,BC=10米.则楼高CD是( )
A.8米 B.7.5米 C.9.5米 D.9米
6.如图,在平行四边形ABCD中,E是AD上一点,连接CE并延长交BA的延长线于点F,则下列结论中错误的是( )
A.∠AEF=∠DEC B.FA:CD=AE:BC
C.FA:AB=FE:EC D.AB=DC
7.△ABC中,D、E分别是边AB、AC上的点,且DE∥BC,已知,那么等于( )
A. B. C. D.
8.已知线段a、b,求作线段x,使,正确的作法是( )
A. B.
C. D.
9.如图,在△ABC中,D、E分别是AB、AC上一点,下面有四个条件:
(1);(2);(3);(4).
其中一定能判定DE∥BC有( )
A.1个 B.2个 C.3个 D.4个
10.如图,在△ABC中,AD是BC边上的中线,E在AC边上,且AE:EC=1:2,BE交AD于P,则AP:PD等于( )
A.1:1 B.1:2 C.2:3 D.4:3
二.填空题(共5小题,满分30分)
11.如图,点A1,A2,A3,A4在射线OA上,点B1,B2,B3在射线OB上,且A1B1∥A2B2∥A3B3,A2B1∥A3B2∥A4B3.若△A2B1B2,△A3B2B3的面积分别为1,9,则图中三个阴影三角形面积之和为 .
12.如图,△ABC的面积是63,D是BC上的一点,且BD:CD=2:1,DE∥AC交AB于E,延长DE到F,使FE:ED=2:1,则△CDF的面积是 .
13.如图,已知:△ABC中,DE∥BC,AD=3,DB=6,AE=2,则EC= .
14.如图,已知点O是△ABC中BC边上的中点,且,则= .
15.将边长分别为2、3、5的三个正方形按图所示的方式排列,则图中阴影部分的面积为 .
三.解答题(共5小题,满分40分)
16.△ABC中,AB=1,AC=2,D是BC中点,AE平分∠BAC交BC于E,且DF∥AE.求CF的长.
17.已知:正方形ABCD,GF∥BE,求证:EF AE=BE EC.
18.探究:如图,四边形ABCD中,AB∥CD,E为AD的中点,若EF∥AB.求证:BF=CF
知识应用:如图,坐标平面内有两个点A和B其中点A的坐标为(x1,y1),点B的坐标为(x2,y2),求AB的中点C的坐标.
知识拓展:在上图中,点A的坐标为(4,5),点B的坐标为(﹣6,﹣1),分别在x轴和y轴上找一点C和D,使得以A、B、C、D为顶点的四边形是平行四边形,求出点C和点D的坐标.
19.已知:线段OA⊥OB,点C为OB中点,D为线段OA上一点.连接AC,BD交于点P.
(1)如图1,当OA=OB,且D为OA中点时,求的值;
(2)如图2,当OA=OB,且时,求的值.
(3)如图3,当AD:AO:OB=1:n:时,直接写出tan∠BPC的值.
20.如图1,∠ACB=90°,CD⊥AB,垂足为D,点E在AC上,BE交CD于点G,EF⊥BE交AB于点F,若AC=mBC,CE=kEA,探索线段EF与EG的数量关系,并证明你的结论.
说明:如果你反复探索没有解决问题,可以选取(1)或(2)中的条件,选(1)中的条件完成解答满分为7分;选(2)中的条件完成解答满分为5分.
(1)m=1(如图2)
(2)m=1,k=1(如图3)
参考答案
一.选择题(共10小题,满分50分)
1.解:∵l1∥l2∥l3,
∴,
即,
解得:EF=6.
故选:C.
2.解:
过B作BM∥DC交AC的延长线于M,
∵DC∥BM,
∴=,
∵AD:BD=1:1,
∴AC=CM,
∵AE:CE=1:2,
∴=,
∵DC∥BM,
∴==,
故选:D.
3.解:连接PP′交BC于O,
∵若四边形QPCP′为菱形,
∴PP′⊥QC,
∴∠POQ=90°,
∵∠ACB=90°,
∴PO∥AC,
∴=,
∵设点Q运动的时间为t秒,
∴AP=t,QB=t,
∴QC=6﹣t,
∴CO=3﹣,
∵AC=CB=6,∠ACB=90°,
∴AB=6,
∴=,
解得:t=2,
故选:B.
4.解:∵四边形ABCD是平行四边形,
∴BC=AD=6cm,BC∥AD.
∴∠EAF=∠EBH,∠AFE=∠BHE,
又AE=BE,
∴△AFE≌△BHE,
∴BH=AF=2cm.
∵BC∥AD,
∴,
即,
则CG=12,
则AC=AG+CG=15(cm).
故选:C.
5.解:由题意可得,BE∥CD,
所以,即,
解得CD=9米,故选D.
6.解:A、根据对顶角相等,此结论正确;
B、根据平行线分线段成比例定理,得FA:FB=AE:BC,所以此结论错误;
C、根据平行线分线段成比例定理得,此项正确;
D、根据平行四边形的对边相等,所以此项正确.
故选:B.
7.解:∵DE∥BC,
∴,
又∵,
∴,
∴=.故选:D.
8.解:由题意,
∴,
∵线段x没法先作出,
∴B选项错误,
根据平行线分线段成比例定理,只有C符合.
故选:C.
9.解:根据对应线段成比例两直线平行,
有,
得到(1)(2)(3)正确,(4)的线段不对应(如图所示)DE′=DE时,DE′不平行于BC,所以不正确.故选:C.
10.解:过点D作DF∥BE,交AC于F,
∴AD是BC边上的中线,
即BD=CD,
∴EF=CF,
∵AE:EC=1:2,
∴AE=EF=FC,
∴AE:EF=1:1,
∴AP:PD=AE:EF=1:1.故选:A.
二.填空题(共5小题,满分30分)
11.解:△A2B1B2,△A3B2B3的面积分别为1,9,
又∵A2B2∥A3B3,A2B1∥A3B2,
∴∠OB2A2=∠OB3A3,∠A2B1B2=∠A3B2B3,
∴△B1B2A2∽△B2B3A3,
==,
∴=.
∵=,△A3B2B3的面积是9,
∴△A2B2A3的面积为=×S△A3B2B3=×9=3(等高的三角形的面积的比等于底边的比).
同理可得:△A3B3A4=3×S△A3B2B3=3×9=27;
△A1B1A2的面积=S△A2B1B2=×1=.
故三个阴影面积之和=+3+27=30.
故答案为:30.
12.方法一:
解:连接CE,因为BD:CD=2:1,所以△BDE和△CDE的面积之比为2:1,
又因为DE∥AC,
∴=,
∴S△BDE:S△ABC=4:9,
又因为△ABC的面积是63,
∴△BDE的面积为:28,
所以△CDE的面积为14,
因为FE:ED=2:1,所以△FDC和△CDE的面积之比为3:1
故答案为:42.
方法二:解:作MW⊥BC,AN⊥BC,垂足分别为W,N.
∵BD:CD=2:1,DE∥AC,
∴BE:AE=2:1,
∴BD:BC=DE:AC=BE:AB=2:3,
∴S△BDE:S△ABC=4:9,
∴S△BDE=×63=28,
∵FE:ED=2:1=4:2,
∴EF:AC=4:3,
∴S△MEF:S△AMC=16:9,
∴EM:AM=4:3,
假设EM=4x,AM=3x,BE=AB=2AE=2(EM+AM)=14x,
∴BM:AM=18x:3x=18:3,
∴MW:AN=BM:AB=18:21=6:7,
∴S△BMC:S△ABC=BC WM:BC AN=WM:AN=6:7,
∵S△ABC=63,
∴S△BMC=54,
∴S△AMC=63﹣54=9,
∵S△MEF:S△AMC=16:9,
∴S△MEF=16,
∵S△BDE=×63=28,
∴S四边形MEDC=63﹣9﹣28=26,
∴△CDF的面积是:26+16=42.
故答案为:42.
13.解:∵△ABC中,DE∥BC,
∴,
∵AD=3,DB=6,AE=2,
∴,
∴EC=4.
故答案为:4.
14.解:过B作BF∥AC,交DE于点F,
∵BF∥AC,
∴∠FBO=∠C,∠BFO=∠CEO,
又O为BC的中点,∴BO=CO,
在△OBF和△OCE中,
,
∴△OBF≌△OCE(AAS),
∴BF=CE,
∵=,∴=,
又∵BF∥AE,∴==,
∴=,
则==.
故答案为:.
15.解:∵VB∥ED,三个正方形的边长分别为2、3、5,
∴VB:DE=AB:AD,即VB:5=2:(2+3+5)=1:5,
∴VB=1,
∵CF∥ED,
∴CF:DE=AC:AD,即CF:5=5:10
∴CF=2.5,
∵S梯形VBFC=(BV+CF) BC=,
∴阴影部分的面积=S正方形BCQW﹣S梯形VBCF=.
故答案为:
三.解答题(共5小题,满分40分)
16.解:分别过E作EH⊥AB于H,EG⊥AC于G,因AE平分∠BAC,所以有EH=EG.
从而有.
又由DF∥AE,得
所以CF=CA==.
17.证明:∵四边形ABCD是正方形,
∴AB∥CD,AD∥BC,
∵GF∥BE,
∴GF∥CD,
∴,
同理:,
∴,
∴EF AE=BE EC.
18.【探究】证明:过点F作GH∥AD,交AB于H,交DC的延长线于点G,
∵AH∥EF∥DG,AD∥GH,
∴四边形AHFE和四边形DEFG都是平行四边形,
∴FH=AE,FG=DE,
∵AE=DE,
∴FG=FH,
∵AB∥DG,
∴∠G=∠FHB,∠GCF=∠B,
∴△CFG≌△BFH,
∴FC=FB;
【知识应用】过点C作CM⊥x轴于点M,过点A作AN⊥x轴于点N,过点B作BP⊥x轴于点P,
则点P的坐标为(x2,0),点N的坐标为(x1,0),
由探究的结论可知,MN=MP,
∴点M的坐标为(,0),
∴点C的横坐标为,
同理可求点C的纵坐标为,
∴点C的坐标为(,).
【知识拓展】
①当AB是平行四边形一条边,且点C在x轴的正半轴时,AD与BC互相平分,
设点C的坐标为(a,0),点D的坐标为(0,b)
由上面的结论可知:﹣6+a=4+0,﹣1+0=5+b,
∴a=10,b=﹣6,
∴此时点C的坐标为(10,0),点D的坐标为(0,﹣6),
②同理,当AB是平行四边形一条边,且点C在x轴的负半轴时,求得点C的坐标为(﹣10,0),点D的坐标为(0,6),
③当AB是对角线时点C的坐标为(﹣2,0),点D的坐标为(0,4).
19.
解:(1)过D作DE∥CO交AC于E,
∵D为OA中点,
∴AE=CE=,,
∵点C为OB中点,
∴BC=CO,,
∴,
∴PC==,
∴=2;
(2)过点D作DE∥BO交AC于E,
∵,
∴==,
∵点C为OB中点,
∴,
∴,
∴PC==,
过D作DF⊥AC,垂足为F,设AD=a,则AO=4a,
∵OA=OB,点C为OB中点,
∴CO=2a,
在Rt△ACO中,AC===2a,
又∵Rt△ADF∽Rt△ACO,
∴,
∴AF=,DF=,
PF=AC﹣AF﹣PC=2a﹣﹣=,
=.
(3)与(2)的方法相同,设AD=a,求出DF=a,
PF=a,所以tan∠BPC=.
20.解:过E作EM⊥AB,EN⊥CD,
∵CD⊥AB,∴EM∥CD,EN∥AB,
∵EF⊥BE,∴∠EFM+∠EBF=90°,
∵∠EBF+∠DGB=90°,∠DGB=∠EGN(对顶角相等)
∴∠EFM=∠EGN,
∴,
在△ADC中,
∵EM∥CD,
∴,
又CE=kEA,
∴AC=(k+1)AE
∴CD=(k+1)EM,
同理,
∴AD=EN,
∵∠ACB=90°,CD⊥AB,AC=mBC
∴,
∴EF=EG.
同课章节目录
- 第23章 数据分析
- 23.1 平均数与加权平均数
- 23.2 中位数与众数
- 23.3 方差
- 23.4 用样本估计总体
- 第24章 一元二次方程
- 24.1 一元二次方程
- 24.2 解一元二次方程
- 24.3 一元二次方程根与系数的关系
- 24.4 一元二次方程的应用
- 第25章 图形的相似
- 25.1 比例线段
- 25.2 平行线分线段成比例
- 25.3 相似三角形
- 25.4 相似三角形的判定
- 25.5 相似三角形的性质
- 25.6 相似三角形的应用
- 25.7 相似多边形和图形的位似
- 第26章 解直角三角形
- 26.1 锐角三角函数
- 26.2 锐角三角函数的计算
- 26.3 解直角三角形
- 26.4 解直角三角形的应用
- 第27章 反比例函数
- 27.1 反比例函数
- 27.2 反比例函数的图像和性质
- 27.3 反比例函数的应用
- 第28章 圆
- 28.1 圆的概念和性质
- 28.2 过三点的圆
- 28.3 圆心角和圆周角
- 28.4 垂径定理
- 28.5 弧长和扇形面积
