北师版2021-2022学年九上数学4.1成比例线段课件(共27张PPT)
文档属性
| 名称 | 北师版2021-2022学年九上数学4.1成比例线段课件(共27张PPT) |  | |
| 格式 | ppt | ||
| 文件大小 | 1.3MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-10-19 17:38:00 | ||
图片预览







文档简介
(共27张PPT)
1 比例线段
第四章 图形的相似
第1课时 线段的比和成比例线段
1.知道线段的比的概念,会计算两条线段的比;(重点)
2.理解成比例线段的概念;(重点)
3.掌握成比例线段的判定方法.(难点)
学习目标
问题1 下面两张邮票有什么特点?有什么关系?
导入新课
观察与思考
问题2 多啦A梦的2寸照片和4寸照片,它的形状改变了吗?大小呢?
讲授新课
线段的比和成比例线段
一
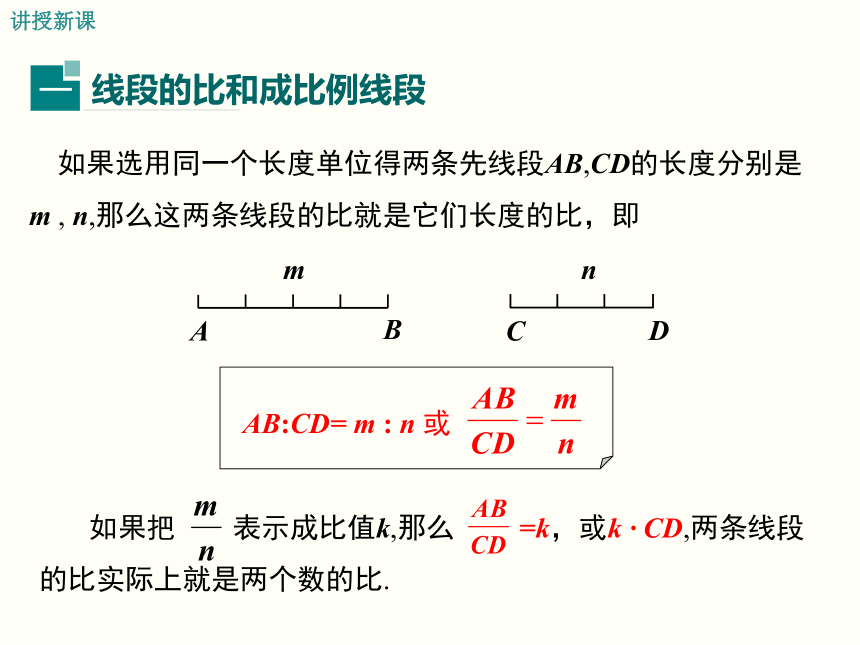
如果选用同一个长度单位得两条先线段AB,CD的长度分别是m , n,那么这两条线段的比就是它们长度的比,即
A
B
C
D
m
n
AB:CD= m : n 或
如果把 表示成比值k,那么 =k,或k · CD,两条线段的比实际上就是两个数的比.
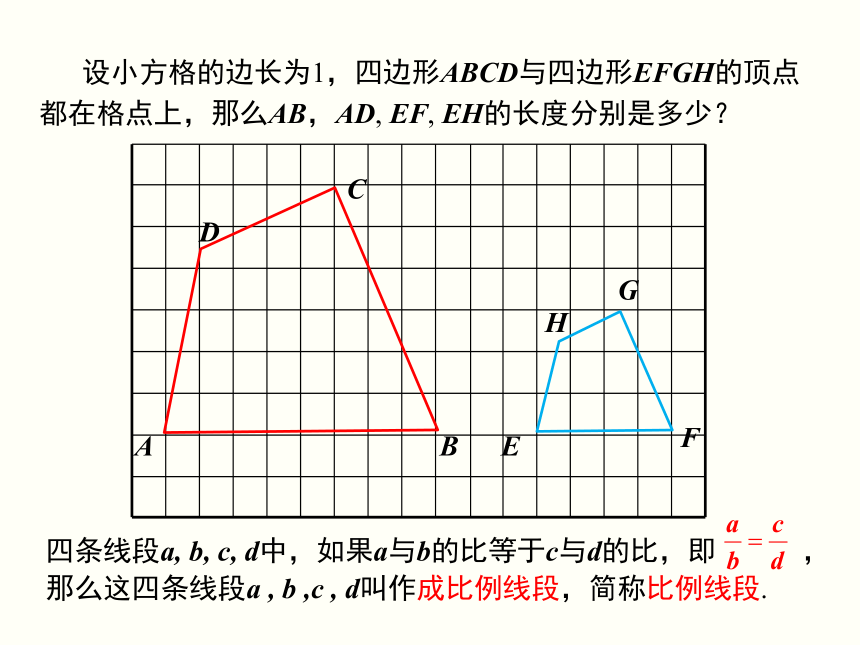
设小方格的边长为1,四边形ABCD与四边形EFGH的顶点都在格点上,那么AB,AD, EF, EH的长度分别是多少?
四条线段a, b, c, d中,如果a与b的比等于c与d的比,即 ,那么这四条线段a , b ,c , d叫作成比例线段,简称比例线段.
A
B
C
D
G
H
E
F
,那么
、
各等于多少?
2.已知
1.已知: 线段a、b、c满足关系式
且b=4,那么ac=______.
,
练一练
16
例:判断下列线段a、b、c、d是否是成比例线段:
(1)a=4,b=6,c=5,d=10;
解: (1) ∵
∴ 线段a、b、c、d 不是成比例线段.
,
∴
,
典例精析
(2)a=2,b=
,c=
,d=
.
(2) ∵
∴
∴ 线段a、b、c、d是成比例线段.
注意:
1.若a:b=k , 说明a是b的 k 倍;
2.两条线段的比与所采用的长度单位无关,但求比时两
条线段的长度单位必须一致;
3.两条线段的比值是一个没有单位的正数;
4.除了a=b外,a:b≠b:a,
互为倒数.
解:根据题意可知AE= am,
由 ,得
即 .
成比例线段的应用
二
例:一块矩形绸布的长AB=am,宽AD=1m,按照图中所示中方式它裁剪成相同的三面矩形彩旗,且使才裁出的每面彩旗的宽与长的比与原绸布的宽与长的比相同,即 ,那么a的值应当是多少?
D
A
F
E
C
B
开平方,得
当堂练习
1.一把矩形米尺,长1m,宽3cm,则这把米尺的长和宽的比
为( )
A.100:3 B.1:3 C.10:3 D.1000:3
2.甲、乙两地相距35km,图上距离为7cm,则这张图的比例
尺为( )
A.5:1 B. 1:5 C.1:500000 D.500000:1
A
C
解:根据题意可知 ,
AB = 15 , AC = 10 , BD = 6.
则 AD = AB – BD =15 – 6= 9.
则
3.已知 ,AB=15,AC=10,BD=6.求AE.
A
B
C
D
E
课堂小结
成比例线段
如果选用同一长度单位量得两条线段AB,CD的长
度分别是m,n,那么这两条线段的比就是它们长
度的比,即AB:CD=m:n,或写成
四条线段a,b,c,d,如果a与b的比等于c与d的
比,即 ,那么这四条线段a,b,c,d叫做
成比例线段,简称比例线段.
线段的比
成比例线段
1 成比例线段
第四章 图形的相似
第2课时 比例的性质
1.理解并掌握比例的基本性质和等比性质;(重点)
2.能运用比例的性质进行相关计算,能通过比例变形解决一些
实际问题.(难点)
学习目标
导入新课
观察与思考
如图的(1)和(2)都是故宫太和殿的照片,(2)是由(1)缩小得到的.
(1)
(2)
P
Q
P′
Q′
在照片(1)中任意取四个点P,Q,A , B在照片(2)
找出对应的两个点P′,Q′,A ′, B ′量出线段PQ,P′Q′,AB, A′B′的长度.计算它们的长度的比值.
A
A
B
B
一般地,如果选用同一长度单位量得两条线段PQ, P′Q′的长度分别为m,n,那么把长度的比 叫作这两条线段PQ与P′Q′的比,记作
,或PQ:
其中PQ, 分别叫作比的前项、后项,如果 的比值为k,那么也可写成
,或
图中,对于另外两条线段有:
讲授新课
比例的基本性质
一
合作探究
问题1:如果四个数a , b, c, d成比例,那么ad = bc吗?反过来如果ad = bc,那么a , b, c , d四个数成比例吗?
如果四个数a,b,c,d成比例,即
那么ad=bc吗?
在等式两边同时乘以bd,得ad=bc
由此可得到比例的基本性质:
如果 ,那么 ad=bc.
由此可得到比例的基本性质:
如果ad=bc(a,b,c,d都不等于0),那么 .
如果ad=bc,那么等式 还成立吗?
在等式中,四个数a,b,c,d可以为任意数,而在分式中,分母不能为0.
典例精析
例1:根据下列条件,求 a : b 的值:
(1) 4a=5b ;
(2)
解 (1)∵ 4a=5b,∴
(2)∵ ,∴8a=7b,∴
例2:已知 ,求 的值.
解:解法1:由比例的基本性质,
得 2(a+3b)=7×2b.
∴a=4b,∴ = 4.
解法2:由 ,得 .
∴ ,
问题2:已知a , b, c, d, e, f 六个数,如果 (b+d+f≠0),那么 成立吗?为什么?
设 ,则
a = kb, c = kd , e= kf .
所以
等比性质
二
例3:在△ABC与△DEF中,已知 ,且△ABC的周长为18cm,求△DEF得周长.
解:∵
∴
∴4(AB + BC + CA)=3 (DE + EF + FD).
即 AB+BC+CA = (DE+EF+FD) ,
又 △ABC的周长为18cm, 即 AB+BC+CA=18cm.
∴ △DEF的周长为24cm.
1.(1)已知 ,那么 = , = .
(3)如果 ,那么 .
(2)如果 那么 .
当堂练习
2.已知四个数a,b,c,d成比例.
(1)若a=-3,b=9,c=2,求d;
(2)若a=-3,b= ,c=2,求d.
1 比例线段
第四章 图形的相似
第1课时 线段的比和成比例线段
1.知道线段的比的概念,会计算两条线段的比;(重点)
2.理解成比例线段的概念;(重点)
3.掌握成比例线段的判定方法.(难点)
学习目标
问题1 下面两张邮票有什么特点?有什么关系?
导入新课
观察与思考
问题2 多啦A梦的2寸照片和4寸照片,它的形状改变了吗?大小呢?
讲授新课
线段的比和成比例线段
一
如果选用同一个长度单位得两条先线段AB,CD的长度分别是m , n,那么这两条线段的比就是它们长度的比,即
A
B
C
D
m
n
AB:CD= m : n 或
如果把 表示成比值k,那么 =k,或k · CD,两条线段的比实际上就是两个数的比.
设小方格的边长为1,四边形ABCD与四边形EFGH的顶点都在格点上,那么AB,AD, EF, EH的长度分别是多少?
四条线段a, b, c, d中,如果a与b的比等于c与d的比,即 ,那么这四条线段a , b ,c , d叫作成比例线段,简称比例线段.
A
B
C
D
G
H
E
F
,那么
、
各等于多少?
2.已知
1.已知: 线段a、b、c满足关系式
且b=4,那么ac=______.
,
练一练
16
例:判断下列线段a、b、c、d是否是成比例线段:
(1)a=4,b=6,c=5,d=10;
解: (1) ∵
∴ 线段a、b、c、d 不是成比例线段.
,
∴
,
典例精析
(2)a=2,b=
,c=
,d=
.
(2) ∵
∴
∴ 线段a、b、c、d是成比例线段.
注意:
1.若a:b=k , 说明a是b的 k 倍;
2.两条线段的比与所采用的长度单位无关,但求比时两
条线段的长度单位必须一致;
3.两条线段的比值是一个没有单位的正数;
4.除了a=b外,a:b≠b:a,
互为倒数.
解:根据题意可知AE= am,
由 ,得
即 .
成比例线段的应用
二
例:一块矩形绸布的长AB=am,宽AD=1m,按照图中所示中方式它裁剪成相同的三面矩形彩旗,且使才裁出的每面彩旗的宽与长的比与原绸布的宽与长的比相同,即 ,那么a的值应当是多少?
D
A
F
E
C
B
开平方,得
当堂练习
1.一把矩形米尺,长1m,宽3cm,则这把米尺的长和宽的比
为( )
A.100:3 B.1:3 C.10:3 D.1000:3
2.甲、乙两地相距35km,图上距离为7cm,则这张图的比例
尺为( )
A.5:1 B. 1:5 C.1:500000 D.500000:1
A
C
解:根据题意可知 ,
AB = 15 , AC = 10 , BD = 6.
则 AD = AB – BD =15 – 6= 9.
则
3.已知 ,AB=15,AC=10,BD=6.求AE.
A
B
C
D
E
课堂小结
成比例线段
如果选用同一长度单位量得两条线段AB,CD的长
度分别是m,n,那么这两条线段的比就是它们长
度的比,即AB:CD=m:n,或写成
四条线段a,b,c,d,如果a与b的比等于c与d的
比,即 ,那么这四条线段a,b,c,d叫做
成比例线段,简称比例线段.
线段的比
成比例线段
1 成比例线段
第四章 图形的相似
第2课时 比例的性质
1.理解并掌握比例的基本性质和等比性质;(重点)
2.能运用比例的性质进行相关计算,能通过比例变形解决一些
实际问题.(难点)
学习目标
导入新课
观察与思考
如图的(1)和(2)都是故宫太和殿的照片,(2)是由(1)缩小得到的.
(1)
(2)
P
Q
P′
Q′
在照片(1)中任意取四个点P,Q,A , B在照片(2)
找出对应的两个点P′,Q′,A ′, B ′量出线段PQ,P′Q′,AB, A′B′的长度.计算它们的长度的比值.
A
A
B
B
一般地,如果选用同一长度单位量得两条线段PQ, P′Q′的长度分别为m,n,那么把长度的比 叫作这两条线段PQ与P′Q′的比,记作
,或PQ:
其中PQ, 分别叫作比的前项、后项,如果 的比值为k,那么也可写成
,或
图中,对于另外两条线段有:
讲授新课
比例的基本性质
一
合作探究
问题1:如果四个数a , b, c, d成比例,那么ad = bc吗?反过来如果ad = bc,那么a , b, c , d四个数成比例吗?
如果四个数a,b,c,d成比例,即
那么ad=bc吗?
在等式两边同时乘以bd,得ad=bc
由此可得到比例的基本性质:
如果 ,那么 ad=bc.
由此可得到比例的基本性质:
如果ad=bc(a,b,c,d都不等于0),那么 .
如果ad=bc,那么等式 还成立吗?
在等式中,四个数a,b,c,d可以为任意数,而在分式中,分母不能为0.
典例精析
例1:根据下列条件,求 a : b 的值:
(1) 4a=5b ;
(2)
解 (1)∵ 4a=5b,∴
(2)∵ ,∴8a=7b,∴
例2:已知 ,求 的值.
解:解法1:由比例的基本性质,
得 2(a+3b)=7×2b.
∴a=4b,∴ = 4.
解法2:由 ,得 .
∴ ,
问题2:已知a , b, c, d, e, f 六个数,如果 (b+d+f≠0),那么 成立吗?为什么?
设 ,则
a = kb, c = kd , e= kf .
所以
等比性质
二
例3:在△ABC与△DEF中,已知 ,且△ABC的周长为18cm,求△DEF得周长.
解:∵
∴
∴4(AB + BC + CA)=3 (DE + EF + FD).
即 AB+BC+CA = (DE+EF+FD) ,
又 △ABC的周长为18cm, 即 AB+BC+CA=18cm.
∴ △DEF的周长为24cm.
1.(1)已知 ,那么 = , = .
(3)如果 ,那么 .
(2)如果 那么 .
当堂练习
2.已知四个数a,b,c,d成比例.
(1)若a=-3,b=9,c=2,求d;
(2)若a=-3,b= ,c=2,求d.
同课章节目录
- 第一章 特殊平行四边形
- 1 菱形的性质与判定
- 2 矩形的性质与判定
- 3 正方形的性质与判定
- 第二章 一元二次方程
- 1 认识一元二次方程
- 2 用配方法求解一元二次方程
- 3 用公式法求解一元二次方程
- 4 用因式分解法求解一元二次方程
- 5 一元二次方程的根与系数的关系
- 6 应用一元二次方程
- 第三章 概率的进一步认识
- 1 用树状图或表格求概率
- 2 用频率估计概率
- 第四章 图形的相似
- 1 成比例线段
- 2 平行线分线段成比例
- 3 相似多边形
- 4 探索三角形相似的条件
- 5 相似三角形判定定理的证明
- 6 利用相似三角形测高
- 7 相似三角形的性质
- 8 图形的位似
- 第五章 投影与视图
- 1 投影
- 2 视图
- 第六章 反比例函数
- 1 反比例函数
- 2 反比例函数的图象与性质
- 3 反比例函数的应用
