北师版2021春九下数学1.2 30°,45°,60°角的三角函数值课件(共14张PPT)
文档属性
| 名称 | 北师版2021春九下数学1.2 30°,45°,60°角的三角函数值课件(共14张PPT) |  | |
| 格式 | ppt | ||
| 文件大小 | 660.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-10-19 17:28:39 | ||
图片预览






文档简介
(共14张PPT)
2 30o,45o,60o角的三角函数值
复习回顾
在Rt△ABC中,如果锐角A确定,那么∠A的对边与斜边的比、邻边与斜边比、对边与邻边的比也随之确定,分别叫做∠A的正弦、余弦、正切.
A
B
C
c
b
a
┌
sinA= , cosA= , tanA=
如图,观察一副三角板:
它们其中有几个锐角 分别是多少度
(1)sin300等于多少
┌
┌
300
600
450
450
(2)cos300等于多少
(3)tan300等于多少
请与同伴交流你是怎么想的 又是怎么做的
引入新知
(5)sin450,sin600等于多少
(6)cos450,cos600等于多少
(7)tan450,tan600等于多少
┌
┌
300
600
450
450
老师期望:
你能对伴随九个学年的这副三角尺所具有的功能来个重新认识和评价.
引入新知
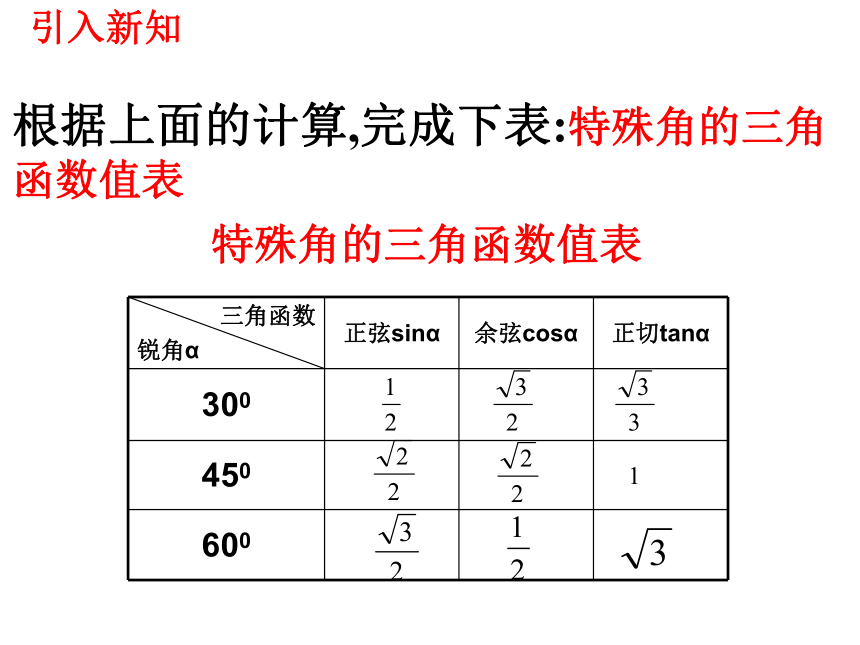
特殊角的三角函数值表
三角函数
锐角α 正弦sinα 余弦cosα 正切tanα
300
450
600
根据上面的计算,完成下表:特殊角的三角函数值表
引入新知
例1 计算:
(1)sin300+cos450;(2) sin2600+sin2300-tan450.
老师提示:
Sin2600表示(sin600)2,
cos2600表示(cos600)2,其余类推.
解: (1)sin300+cos450
(2) sin2600+sin2300-tan450
例题解析
(1)sin600-cos450;(2)cos600+tan600
1计算:
课内练习
例2 如图:一个小孩荡秋千,秋千链子的长度为2.5m,当秋千向两边摆动时,摆角恰好为600,且两边摆动的角度相同,求它摆至最高位置时与其摆至最低位置时的高度之差(结果精确到0.01m).
∴最高位置与最低位置的高度差约为0.34m.
∠AOD OD=2.5m,
A
C
O
B
D
┌
解:如图,根据题意可知,
∴AC=2.5-2.165≈0.34(m).
●
2.5
例题解析
老师期望:
sin2A+cos2A=1它反映了同角之间的三角函数的关系,且它更具有灵活变换的特点,若能予以掌握,则将有益于智力开发.
2.某商场有一自动扶梯,其倾斜角为300,高为7m,扶梯的长度是多少
3.如图,在Rt△ABC中,∠C=90°,
∠A,∠B ,∠C的对边分别是a,b,c.
求证:sin2A+cos2A=1
b
A
B
C
a
┌
c
课内练习
⒈计算:
⑴ sin60°-tan45°;
⑵ cos60°+tan60°;
⑶ sin45°+sin60°-2cos45°
⒉某商场有一自动扶梯,其倾斜角为30°,高为7m.扶梯的长度是多少
课后练习
直角三角形中的边角关系
小结 拓展
看图说话:
直角三角形三边的关系.
直角三角形两锐角的关系.
直角三角形边与角之间的关系.
特殊角300,450,600角的三角函数值.
互余两角之间的三角函数关系.
同角之间的三角函数关系
b
A
B
C
a
┌
c
┌
┌
300
600
450
450
P10 习题1.3 1,2,3题
课后作业
小阳发现电线杆AB的影子落在土坡的坡面CD和地面BC上,量得CD=8米,BC=20米,CD与地面成30O角,且此时没得1米杆的影长为2米,则电线杆的高度为( )
A.9米
B.28米
链接中考
C.
米
D.
米
C
你一天的爱心可能带来别人一生的感谢。
2 30o,45o,60o角的三角函数值
复习回顾
在Rt△ABC中,如果锐角A确定,那么∠A的对边与斜边的比、邻边与斜边比、对边与邻边的比也随之确定,分别叫做∠A的正弦、余弦、正切.
A
B
C
c
b
a
┌
sinA= , cosA= , tanA=
如图,观察一副三角板:
它们其中有几个锐角 分别是多少度
(1)sin300等于多少
┌
┌
300
600
450
450
(2)cos300等于多少
(3)tan300等于多少
请与同伴交流你是怎么想的 又是怎么做的
引入新知
(5)sin450,sin600等于多少
(6)cos450,cos600等于多少
(7)tan450,tan600等于多少
┌
┌
300
600
450
450
老师期望:
你能对伴随九个学年的这副三角尺所具有的功能来个重新认识和评价.
引入新知
特殊角的三角函数值表
三角函数
锐角α 正弦sinα 余弦cosα 正切tanα
300
450
600
根据上面的计算,完成下表:特殊角的三角函数值表
引入新知
例1 计算:
(1)sin300+cos450;(2) sin2600+sin2300-tan450.
老师提示:
Sin2600表示(sin600)2,
cos2600表示(cos600)2,其余类推.
解: (1)sin300+cos450
(2) sin2600+sin2300-tan450
例题解析
(1)sin600-cos450;(2)cos600+tan600
1计算:
课内练习
例2 如图:一个小孩荡秋千,秋千链子的长度为2.5m,当秋千向两边摆动时,摆角恰好为600,且两边摆动的角度相同,求它摆至最高位置时与其摆至最低位置时的高度之差(结果精确到0.01m).
∴最高位置与最低位置的高度差约为0.34m.
∠AOD OD=2.5m,
A
C
O
B
D
┌
解:如图,根据题意可知,
∴AC=2.5-2.165≈0.34(m).
●
2.5
例题解析
老师期望:
sin2A+cos2A=1它反映了同角之间的三角函数的关系,且它更具有灵活变换的特点,若能予以掌握,则将有益于智力开发.
2.某商场有一自动扶梯,其倾斜角为300,高为7m,扶梯的长度是多少
3.如图,在Rt△ABC中,∠C=90°,
∠A,∠B ,∠C的对边分别是a,b,c.
求证:sin2A+cos2A=1
b
A
B
C
a
┌
c
课内练习
⒈计算:
⑴ sin60°-tan45°;
⑵ cos60°+tan60°;
⑶ sin45°+sin60°-2cos45°
⒉某商场有一自动扶梯,其倾斜角为30°,高为7m.扶梯的长度是多少
课后练习
直角三角形中的边角关系
小结 拓展
看图说话:
直角三角形三边的关系.
直角三角形两锐角的关系.
直角三角形边与角之间的关系.
特殊角300,450,600角的三角函数值.
互余两角之间的三角函数关系.
同角之间的三角函数关系
b
A
B
C
a
┌
c
┌
┌
300
600
450
450
P10 习题1.3 1,2,3题
课后作业
小阳发现电线杆AB的影子落在土坡的坡面CD和地面BC上,量得CD=8米,BC=20米,CD与地面成30O角,且此时没得1米杆的影长为2米,则电线杆的高度为( )
A.9米
B.28米
链接中考
C.
米
D.
米
C
你一天的爱心可能带来别人一生的感谢。
