2021秋北师版九上数学 2.1第2课时估算一元二次方程的近似解(共21张)
文档属性
| 名称 | 2021秋北师版九上数学 2.1第2课时估算一元二次方程的近似解(共21张) |

|
|
| 格式 | ppt | ||
| 文件大小 | 1.5MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-10-19 00:00:00 | ||
图片预览








文档简介
(共21张PPT)
第二章 一元二次方程
认识一元二次方程
第2课时 估算一元二次方程的近似解
对于一元二次方程
(1)(8-2x)(5-2x)=18 即:2x2-13x+11=0;
(2)(x+6)2+72=102 即:x2+12x-15=0,
你能分别求出方程中的x吗?
一、复习回顾
二、情境引入
16枚金币中有一枚略轻,是假币,如何最快的用天平找出,最少几次?
身临其境 体验生活
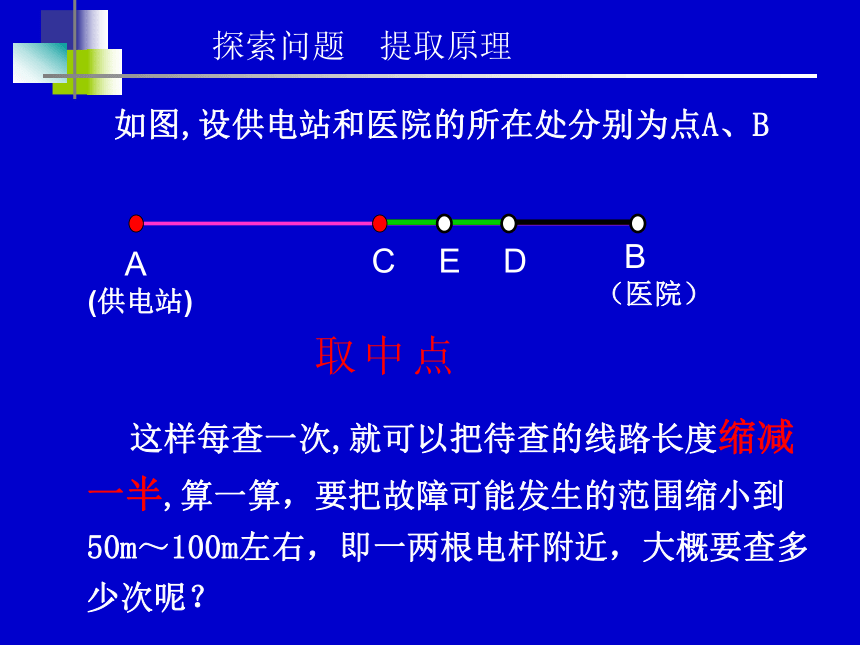
某个雷电交加的夜晚,医院的医生正在抢救一个危重病人,忽然电停了。据了解原因是供电站到医院的某处线路出现了故障,维修工,如何迅速查出故障所在 (线路长10km,每50m一根电线杆)
二、情境引入
提醒:如果沿着线路一小段一小段查找,困难很多,每查一个点要爬一次电线杆子,10km长,大约有200根电线杆子呢。
想一想:维修线路的工人师傅怎样工作最合理?
如图,设供电站和医院的所在处分别为点A、B
A
(供电站)
这样每查一次,就可以把待查的线路长度缩减一半,算一算,要把故障可能发生的范围缩小到50m~100m左右,即一两根电杆附近,大概要查多少次呢?
C
B
(医院)
D
E
探索问题 提取原理
二、情境引入
(1)有一根外带有塑料皮长为100m的电线,不知什么原因中间有一处不通,现给你一只万用表(能测量是否通)进行检查,你怎样快速地找到这一断裂处?与同伴进行交流。
二、情境引入
(2)幼儿园活动教室矩形地面的长为8米,宽为5米,现准备在地面的正中间铺设一块面积为18m2的地毯,四周未铺地毯的条形区域的宽度都相同 ,你能求出这个宽度吗?
解:设所求的宽度为xm , 根据题意,可得方程 (8-2x)(5-2x)=18 即: 2x2-13x+11=0
8
5
x
x
x
x
(8-2x)
(5-2x)
18m2
5
二、情境引入
对于方程(8-2x)(5-2x)=18,即2x2-13x+11=0
(1)根据题目的已知条件,你能确定x的大致范围吗? 说说你的理由.
(2) x可能小于0吗 x可能大于4吗 可能大于2.5吗 说说你的理由,并与同伴进行交流.
(3)完成下表:
(4)你知道所求的宽度x(m)是多少吗 还有其他求解方法吗 与同伴进行交流.
2x2-13x+11
2
1.5
1
0.5
0
x
2.5
二、情境引入
用“夹逼”思想解一元二次方程的步骤:
①在未知数x的取值范围内排除一部分取值;
②根据题意所列的具体情况再次进行排除;
③列出能反映未知数和方程的值的表格进行 再次筛选;
④最终得出未知数的最小取值范围或具体数据。
三、做一做
如图,一个长为10m的梯子斜靠在墙上,梯子的顶端距地面的垂直距离为8m.如果梯子的顶端下滑1m,那么梯子的底端滑动多少米?
x
8m
1
10m
7m
6m
10m
在上一节课的问题中,梯子底端滑动的距离x(m)满足方程(x+6)2+72 =102,把这个方程化为一般形式为 x2+12x-15=0
(1)你能猜出滑动距离x(m)的大致范围吗
(2)小明认为底端也滑动了1 m,他的说法正确吗
为什么
(3)底端滑动的距离可能是2 m吗 可能是3 m吗 为什么
(4)x的整数部分是几 十分位是几
三、做一做
三、做一做
x2+12x-15
13
2
5.25
1.5
-2
1
-8.75
0.5
-15
0
x
甲同学的做法:
所以1<x<1.5
三、做一做
x2+12x-15
13
2
5.25
1.5
-2
1
-8.75
0.5
-15
0
x
进一步计算:
所以1.1<x<1.2
因此x的整数部分是1,十分位是1。
三、做一做
x2+12x-15
5.25
1.5
3.76
1.4
2.29
1.3
0.84
1.2
-0.59
1.1
x
乙同学的做法:
所以1.1<x<1.2
因此x的整数部分是1,十分位是1。
四、练一练
五个连续整数,前三个数的平方和等于后两个数的平方。您能求出这五个整数分别是多少吗?
四、练一练
A同学的做法:
设五个连续整数中的第一个数为x,那么后面四个数依次可表示为x+1,x+2,x+3,x+4.根据题意,可得方程:
x2+(x+1)2+(x+2)2=(x+3)2+(x+4)2
即:x2-8x-20=0
x2-8x-20
0
10
-11
9
…
…
0
-2
13
-3
x
所以,x=-2或x=10
四、练一练
B同学的做法:
设五个连续整数中的中间一个数为x,那么其余四个数
依次可表示为x-2,x-1,x+1,x+2.根据题意,可得方程:(x-2)2+(x-1)2+x2=(x+1)2+(x+2)2
即:x2-12x=0
x2-12x
0
10
-11
9
…
…
0
-2
13
-3
x
所以,x=0或x=12
五、读一读
自己用3-4分钟阅读课本P34页读一读
六、课堂小结
通过本堂课你有哪些收获?谈谈你的感想。
七、作业
课本35页习题2.2 1题、2题
第二章 一元二次方程
认识一元二次方程
第2课时 估算一元二次方程的近似解
对于一元二次方程
(1)(8-2x)(5-2x)=18 即:2x2-13x+11=0;
(2)(x+6)2+72=102 即:x2+12x-15=0,
你能分别求出方程中的x吗?
一、复习回顾
二、情境引入
16枚金币中有一枚略轻,是假币,如何最快的用天平找出,最少几次?
身临其境 体验生活
某个雷电交加的夜晚,医院的医生正在抢救一个危重病人,忽然电停了。据了解原因是供电站到医院的某处线路出现了故障,维修工,如何迅速查出故障所在 (线路长10km,每50m一根电线杆)
二、情境引入
提醒:如果沿着线路一小段一小段查找,困难很多,每查一个点要爬一次电线杆子,10km长,大约有200根电线杆子呢。
想一想:维修线路的工人师傅怎样工作最合理?
如图,设供电站和医院的所在处分别为点A、B
A
(供电站)
这样每查一次,就可以把待查的线路长度缩减一半,算一算,要把故障可能发生的范围缩小到50m~100m左右,即一两根电杆附近,大概要查多少次呢?
C
B
(医院)
D
E
探索问题 提取原理
二、情境引入
(1)有一根外带有塑料皮长为100m的电线,不知什么原因中间有一处不通,现给你一只万用表(能测量是否通)进行检查,你怎样快速地找到这一断裂处?与同伴进行交流。
二、情境引入
(2)幼儿园活动教室矩形地面的长为8米,宽为5米,现准备在地面的正中间铺设一块面积为18m2的地毯,四周未铺地毯的条形区域的宽度都相同 ,你能求出这个宽度吗?
解:设所求的宽度为xm , 根据题意,可得方程 (8-2x)(5-2x)=18 即: 2x2-13x+11=0
8
5
x
x
x
x
(8-2x)
(5-2x)
18m2
5
二、情境引入
对于方程(8-2x)(5-2x)=18,即2x2-13x+11=0
(1)根据题目的已知条件,你能确定x的大致范围吗? 说说你的理由.
(2) x可能小于0吗 x可能大于4吗 可能大于2.5吗 说说你的理由,并与同伴进行交流.
(3)完成下表:
(4)你知道所求的宽度x(m)是多少吗 还有其他求解方法吗 与同伴进行交流.
2x2-13x+11
2
1.5
1
0.5
0
x
2.5
二、情境引入
用“夹逼”思想解一元二次方程的步骤:
①在未知数x的取值范围内排除一部分取值;
②根据题意所列的具体情况再次进行排除;
③列出能反映未知数和方程的值的表格进行 再次筛选;
④最终得出未知数的最小取值范围或具体数据。
三、做一做
如图,一个长为10m的梯子斜靠在墙上,梯子的顶端距地面的垂直距离为8m.如果梯子的顶端下滑1m,那么梯子的底端滑动多少米?
x
8m
1
10m
7m
6m
10m
在上一节课的问题中,梯子底端滑动的距离x(m)满足方程(x+6)2+72 =102,把这个方程化为一般形式为 x2+12x-15=0
(1)你能猜出滑动距离x(m)的大致范围吗
(2)小明认为底端也滑动了1 m,他的说法正确吗
为什么
(3)底端滑动的距离可能是2 m吗 可能是3 m吗 为什么
(4)x的整数部分是几 十分位是几
三、做一做
三、做一做
x2+12x-15
13
2
5.25
1.5
-2
1
-8.75
0.5
-15
0
x
甲同学的做法:
所以1<x<1.5
三、做一做
x2+12x-15
13
2
5.25
1.5
-2
1
-8.75
0.5
-15
0
x
进一步计算:
所以1.1<x<1.2
因此x的整数部分是1,十分位是1。
三、做一做
x2+12x-15
5.25
1.5
3.76
1.4
2.29
1.3
0.84
1.2
-0.59
1.1
x
乙同学的做法:
所以1.1<x<1.2
因此x的整数部分是1,十分位是1。
四、练一练
五个连续整数,前三个数的平方和等于后两个数的平方。您能求出这五个整数分别是多少吗?
四、练一练
A同学的做法:
设五个连续整数中的第一个数为x,那么后面四个数依次可表示为x+1,x+2,x+3,x+4.根据题意,可得方程:
x2+(x+1)2+(x+2)2=(x+3)2+(x+4)2
即:x2-8x-20=0
x2-8x-20
0
10
-11
9
…
…
0
-2
13
-3
x
所以,x=-2或x=10
四、练一练
B同学的做法:
设五个连续整数中的中间一个数为x,那么其余四个数
依次可表示为x-2,x-1,x+1,x+2.根据题意,可得方程:(x-2)2+(x-1)2+x2=(x+1)2+(x+2)2
即:x2-12x=0
x2-12x
0
10
-11
9
…
…
0
-2
13
-3
x
所以,x=0或x=12
五、读一读
自己用3-4分钟阅读课本P34页读一读
六、课堂小结
通过本堂课你有哪些收获?谈谈你的感想。
七、作业
课本35页习题2.2 1题、2题
同课章节目录
- 第一章 特殊平行四边形
- 1 菱形的性质与判定
- 2 矩形的性质与判定
- 3 正方形的性质与判定
- 第二章 一元二次方程
- 1 认识一元二次方程
- 2 用配方法求解一元二次方程
- 3 用公式法求解一元二次方程
- 4 用因式分解法求解一元二次方程
- 5 一元二次方程的根与系数的关系
- 6 应用一元二次方程
- 第三章 概率的进一步认识
- 1 用树状图或表格求概率
- 2 用频率估计概率
- 第四章 图形的相似
- 1 成比例线段
- 2 平行线分线段成比例
- 3 相似多边形
- 4 探索三角形相似的条件
- 5 相似三角形判定定理的证明
- 6 利用相似三角形测高
- 7 相似三角形的性质
- 8 图形的位似
- 第五章 投影与视图
- 1 投影
- 2 视图
- 第六章 反比例函数
- 1 反比例函数
- 2 反比例函数的图象与性质
- 3 反比例函数的应用
