2021秋北师版九下数学 3.9弧长及扇形的面积(共16张)
文档属性
| 名称 | 2021秋北师版九下数学 3.9弧长及扇形的面积(共16张) |  | |
| 格式 | ppt | ||
| 文件大小 | 382.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-10-19 18:36:33 | ||
图片预览




文档简介
(共16张PPT)
3.9 弧长及扇形的面积
创设情境 温故探新
复习
导入
在一块空旷的草地上有一根柱子,柱子上拴着一条长3m的绳子,绳子的一端拴着一只狗.
(1)这只狗的最大活动区域有多大?
这个区域的边缘长是多少?
(2)如果这只狗拴在夹角为120°
的墙角 ,那么它的最大活动区域
有多大?这个区域的边缘长是
多少?
合作交流探究新知
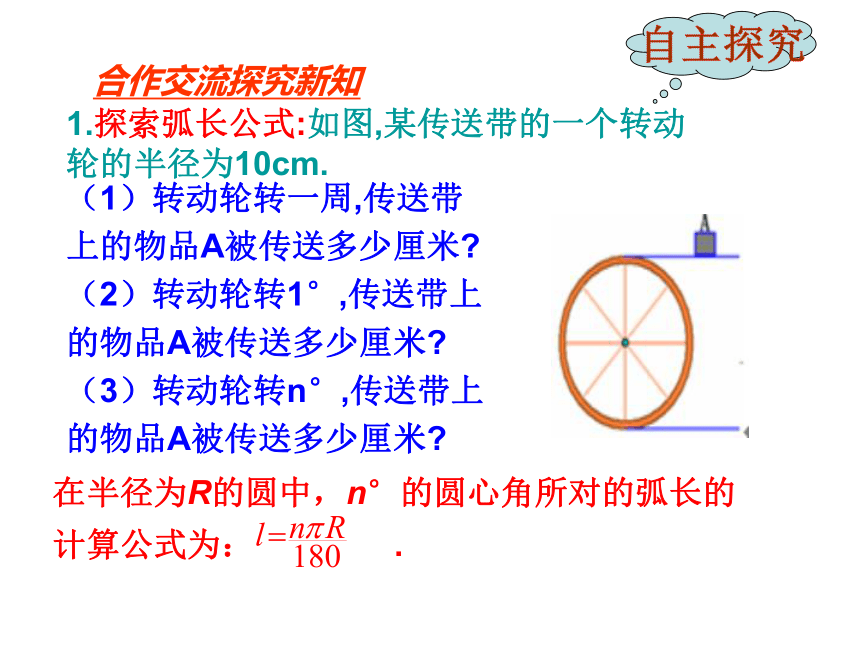
1.探索弧长公式:如图,某传送带的一个转动轮的半径为10cm.
(1)转动轮转一周,传送带上的物品A被传送多少厘米
(2)转动轮转1°,传送带上的物品A被传送多少厘米
(3)转动轮转n°,传送带上的物品A被传送多少厘米
在半径为R的圆中,n°的圆心角所对的弧长的计算公式为: .
合作交流探究新知
2.探索扇形面积公式
(1)观察与思考:怎样的图形是扇形?
(2)扇形面积的大小到底和哪些因素有关呢?
(3)讨论如何求扇形的面积?
①圆心角是1°的扇形面积是圆面积的多少?
②圆心角为n°的扇形面积是圆面积的多少?
合作交流探究新知
如果圆的半径为R,则圆的面积为πR2,1°的圆心角对应的扇形面积为 ,n°的圆心角对应的扇形面积为 .因此扇形面积的计算公式为: ,其中R为扇形的半径,n为圆心角.
合作交流探究新知
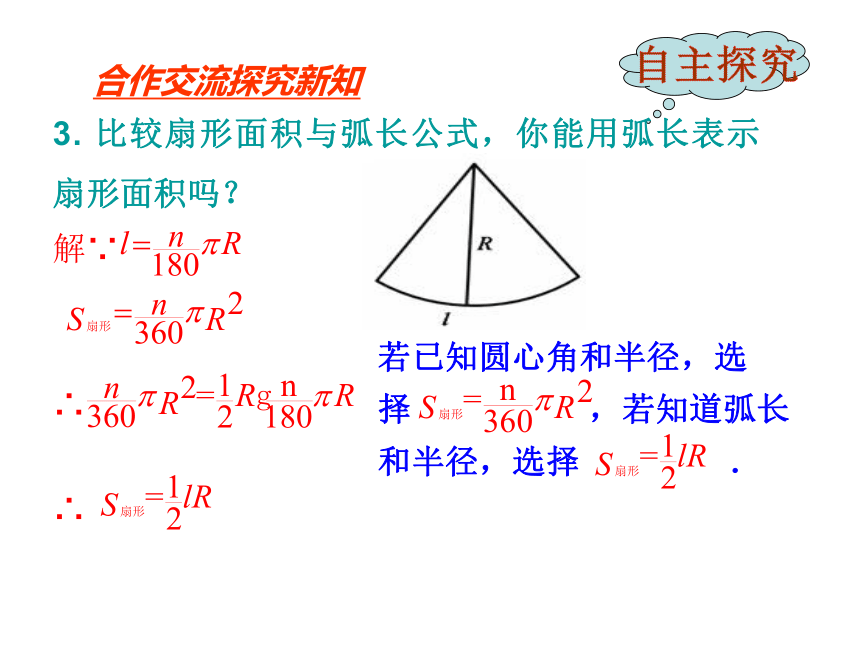
3. 比较扇形面积与弧长公式,你能用弧长表示扇形面积吗?
解∵
∴
∴
若已知圆心角和半径,选择 ,若知道弧长和半径,选择 .
范例研讨运用新知
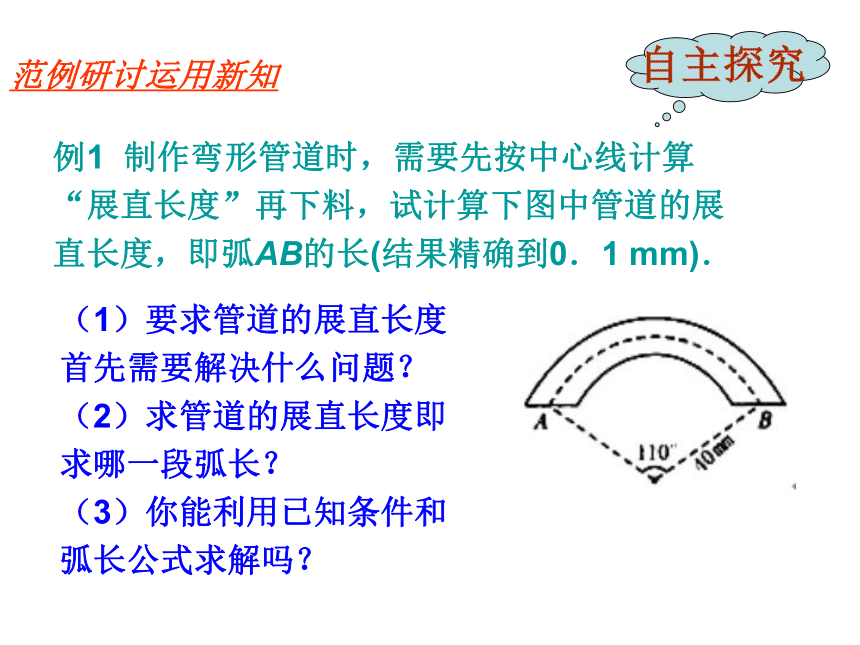
例1 制作弯形管道时,需要先按中心线计算“展直长度”再下料,试计算下图中管道的展直长度,即弧AB的长(结果精确到0.1 mm).
(1)要求管道的展直长度首先需要解决什么问题?
(2)求管道的展直长度即求哪一段弧长?
(3)你能利用已知条件和弧长公式求解吗?
范例研讨运用新知
解:∵R=40mm,n=110°.
∴弧AB的长 mm.
因此,管道的展直长度约为76.8 mm.
范例研讨运用新知
例2 扇形AOB的半径为12 cm,∠AOB=120°,求弧AB的长(结果精确到0.1 cm)和扇形AOB的面积(结果精确到0.1cm2)
(1)题目中给出了哪些已知条件?
(2)这些条件能直接应用于公式吗?
(3)你能利用已知条件和扇形面积公式求解吗?
范例研讨运用新知
解:弧AB的长l= ×π×12=8π≈25.1cm
S扇形= ×π×122=48π≈150.7 cm2.
因此,弧AB的长约为25.1 cm,扇形AOB的面积约为150.7 cm2.
1.(衡阳中考)圆心角为120°,弧长为12π的扇形半径为( )
A.6 B.9 C.18 D.36
2.(湖州中考)如图,已知C,D是以AB为直径的半圆周上的两点,O是圆心,半径OA=2,∠COD=120°,则图中阴影部分的面积等于_______.
反馈练习巩固新知
C
反馈练习巩固新知
3. 如图所示,在四边形ABCD中,AB⊥BC,AC⊥CD,以CD为直径作半圆O,AB=4cm,BC=3cm,AD=13cm.求图中阴影部分的面积.
反馈练习巩固新知
解:∵AB⊥BC,AB=4,BC=3,
∴AC=5.
∵AC⊥CD,AC=5,AD=13,
∴CD=12,
∴S阴影= =18π,
∴阴影部分的面积为18πcm2.
课堂小结布置作业
小结:
(1)n°的圆心角所对的弧长公式:
(2)n°的圆心角所对的扇形面积公式:
(3)半径为R,弧长为l的扇形面积:
课堂小结布置作业
作业:
1.课本101页随堂练习第1、2题.
2.课本102页习题3.11第1、2、3、4题.
3.9 弧长及扇形的面积
创设情境 温故探新
复习
导入
在一块空旷的草地上有一根柱子,柱子上拴着一条长3m的绳子,绳子的一端拴着一只狗.
(1)这只狗的最大活动区域有多大?
这个区域的边缘长是多少?
(2)如果这只狗拴在夹角为120°
的墙角 ,那么它的最大活动区域
有多大?这个区域的边缘长是
多少?
合作交流探究新知
1.探索弧长公式:如图,某传送带的一个转动轮的半径为10cm.
(1)转动轮转一周,传送带上的物品A被传送多少厘米
(2)转动轮转1°,传送带上的物品A被传送多少厘米
(3)转动轮转n°,传送带上的物品A被传送多少厘米
在半径为R的圆中,n°的圆心角所对的弧长的计算公式为: .
合作交流探究新知
2.探索扇形面积公式
(1)观察与思考:怎样的图形是扇形?
(2)扇形面积的大小到底和哪些因素有关呢?
(3)讨论如何求扇形的面积?
①圆心角是1°的扇形面积是圆面积的多少?
②圆心角为n°的扇形面积是圆面积的多少?
合作交流探究新知
如果圆的半径为R,则圆的面积为πR2,1°的圆心角对应的扇形面积为 ,n°的圆心角对应的扇形面积为 .因此扇形面积的计算公式为: ,其中R为扇形的半径,n为圆心角.
合作交流探究新知
3. 比较扇形面积与弧长公式,你能用弧长表示扇形面积吗?
解∵
∴
∴
若已知圆心角和半径,选择 ,若知道弧长和半径,选择 .
范例研讨运用新知
例1 制作弯形管道时,需要先按中心线计算“展直长度”再下料,试计算下图中管道的展直长度,即弧AB的长(结果精确到0.1 mm).
(1)要求管道的展直长度首先需要解决什么问题?
(2)求管道的展直长度即求哪一段弧长?
(3)你能利用已知条件和弧长公式求解吗?
范例研讨运用新知
解:∵R=40mm,n=110°.
∴弧AB的长 mm.
因此,管道的展直长度约为76.8 mm.
范例研讨运用新知
例2 扇形AOB的半径为12 cm,∠AOB=120°,求弧AB的长(结果精确到0.1 cm)和扇形AOB的面积(结果精确到0.1cm2)
(1)题目中给出了哪些已知条件?
(2)这些条件能直接应用于公式吗?
(3)你能利用已知条件和扇形面积公式求解吗?
范例研讨运用新知
解:弧AB的长l= ×π×12=8π≈25.1cm
S扇形= ×π×122=48π≈150.7 cm2.
因此,弧AB的长约为25.1 cm,扇形AOB的面积约为150.7 cm2.
1.(衡阳中考)圆心角为120°,弧长为12π的扇形半径为( )
A.6 B.9 C.18 D.36
2.(湖州中考)如图,已知C,D是以AB为直径的半圆周上的两点,O是圆心,半径OA=2,∠COD=120°,则图中阴影部分的面积等于_______.
反馈练习巩固新知
C
反馈练习巩固新知
3. 如图所示,在四边形ABCD中,AB⊥BC,AC⊥CD,以CD为直径作半圆O,AB=4cm,BC=3cm,AD=13cm.求图中阴影部分的面积.
反馈练习巩固新知
解:∵AB⊥BC,AB=4,BC=3,
∴AC=5.
∵AC⊥CD,AC=5,AD=13,
∴CD=12,
∴S阴影= =18π,
∴阴影部分的面积为18πcm2.
课堂小结布置作业
小结:
(1)n°的圆心角所对的弧长公式:
(2)n°的圆心角所对的扇形面积公式:
(3)半径为R,弧长为l的扇形面积:
课堂小结布置作业
作业:
1.课本101页随堂练习第1、2题.
2.课本102页习题3.11第1、2、3、4题.
