2021—2022学年人教版数学九年级上册22.1.2二次函数y=ax2的图像与性质 课件(18张)
文档属性
| 名称 | 2021—2022学年人教版数学九年级上册22.1.2二次函数y=ax2的图像与性质 课件(18张) |

|
|
| 格式 | zip | ||
| 文件大小 | 616.8KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-10-19 14:08:10 | ||
图片预览



文档简介
(共18张PPT)
愿你们努力进取,永不言败!
致我亲爱的同学们
给我最大快乐的,
不是已懂的知识,
而是不断的学习.
----高斯
人教版义务教育教科书 数学 九年级(上册)
22.1 二次函数y=ax2的图象和性质
复习提问:
(1)一次函数的图象是一条_____.
直线
二次函数的图象是什么形 状呢?
x … -3 -2 -1 0 1 2 3 …
y=x2
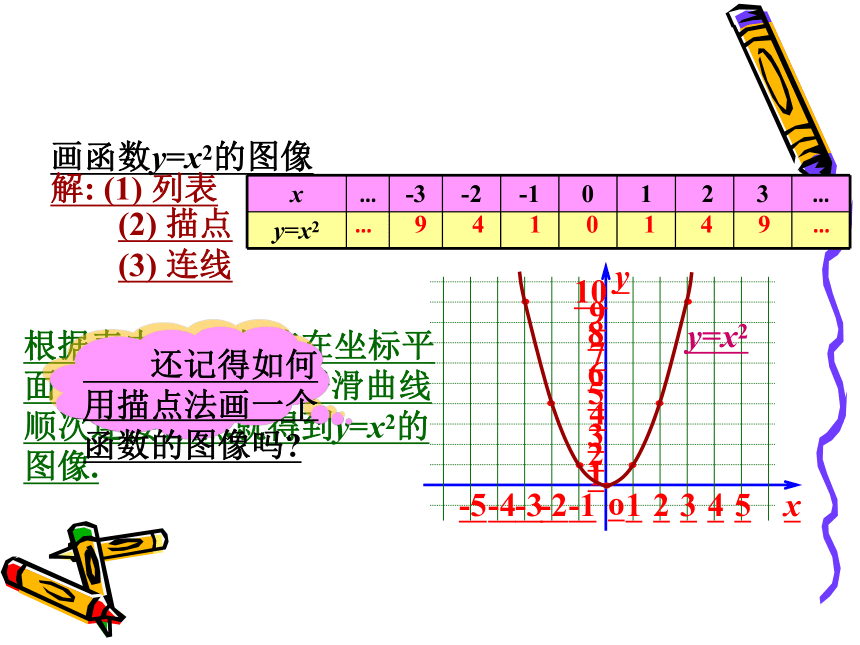
画函数y=x2的图像
解: (1) 列表
… 9 4 1 0 1 4 9 …
(2) 描点
(3) 连线
1
2
3
4
5
x
1
2
3
4
5
6
7
8
9
10
y
o
-1
-2
-3
-4
-5
根据表中x,y的数值在坐标平面中描点(x,y),再用平滑曲线顺次连接各点,就得到y=x2的图像.
还记得如何用描点法画一个函数的图像吗
y=x2
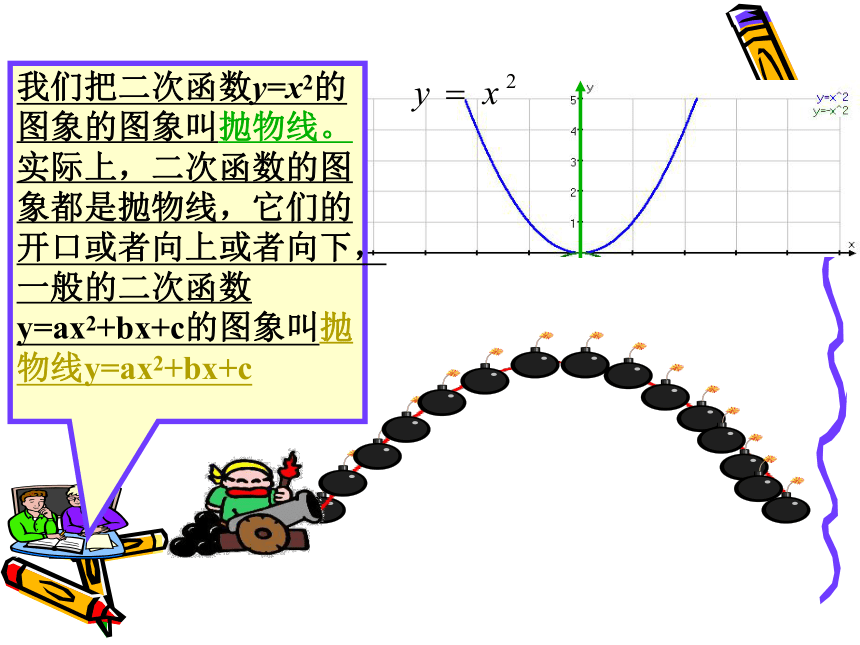
我们把二次函数y=x2的图象的图象叫抛物线。实际上,二次函数的图象都是抛物线,它们的开口或者向上或者向下, 一般的二次函数y=ax2+bx+c的图象叫抛物线y=ax2+bx+c
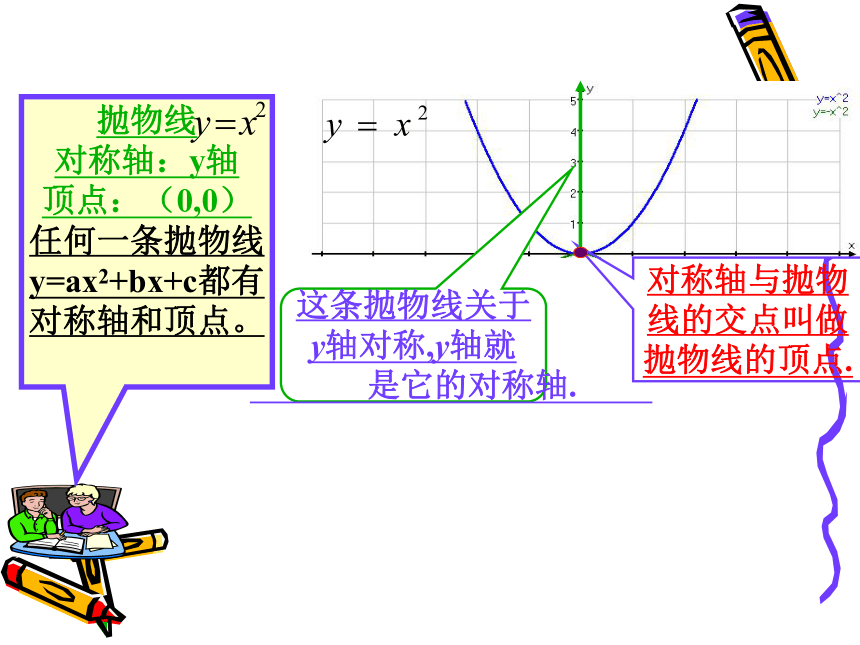
抛物线 对称轴:y轴
顶点:(0,0)
任何一条抛物线y=ax2+bx+c都有对称轴和顶点。
这条抛物线关于
y轴对称,y轴就
是它的对称轴.
对称轴与抛物
线的交点叫做
抛物线的顶点.
x … -4 -3 -2 -1 0 1 2 3 4 …
y= x2
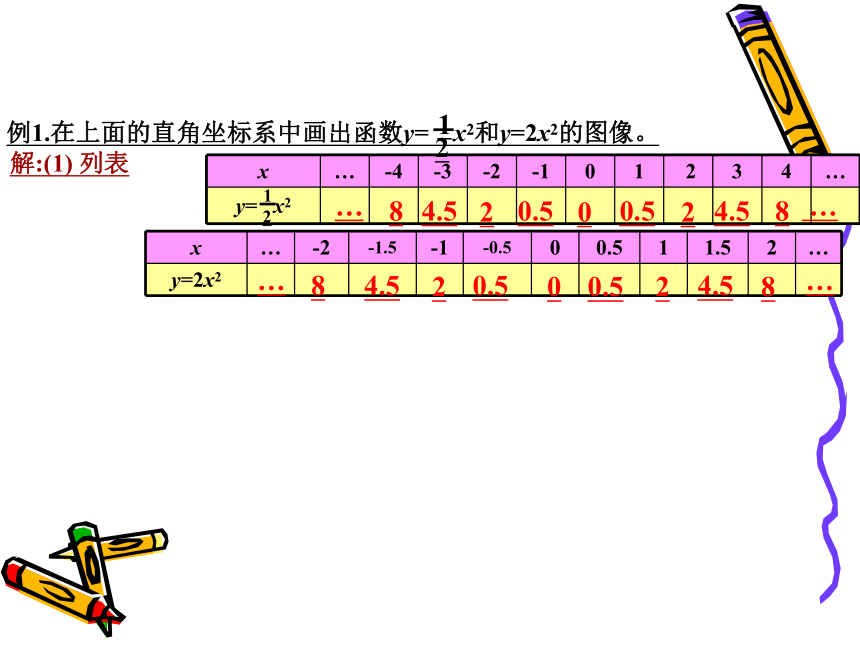
例1.在上面的直角坐标系中画出函数y= x2和y=2x2的图像。
解:(1) 列表
1
2
x … -2 -1.5 -1 -0.5 0 0.5 1 1.5 2 …
y=2x2
8
…
2
0.5
0
0.5
2
4.5
8
…
4.5
8
…
2
0.5
0
0.5
2
4.5
8
…
4.5
1
2
例1.在上面的直角坐标系中画出函数y= x2和y=2x2的图像。
解:(1) 列表
(2) 描点
(3) 连线
1
2
3
4
5
x
1
2
3
4
5
6
7
8
9
10
y
o
-1
-2
-3
-4
-5
1
2
函数y= x2,y=2x2的图像与函数y=x2(图中虚线图形)的图像相比,有什么共同点和不同点
当a>0时,二次函数y=ax2的图像有什么特点
观察
不同点:
共同点:开口向上;对称轴都是y轴;顶点都是原点,顶点是抛物线的最低点
除顶点外,图像都在x轴上方
开口大小不同,
1
2
x … -3 -2 -1 0 1 2 3 …
y=-x2
请画函数y=-x2的图像
解:(1) 列表
… -9 -4 -1 0 -1 -4 -9 …
(2) 描点
(3) 连线
根据表中x,y的数值在坐标平面中描点(x,y),再用平滑曲线顺次连接各点,就得到y=-x2的图像.
1
2
3
4
5
x
-1
-2
-3
-4
-5
-6
-7
-8
-9
1
y
o
-1
-2
-3
-4
-5
-10
y=-x2
1
2
3
4
5
x
1
2
3
4
5
6
7
8
9
10
y
o
-1
-2
-3
-4
-5
y=-x2
当a值相反时,两抛物线的
形状大小相同,开口相反
1
2
3
4
5
x
-1
-2
-3
-4
-5
-6
-7
-8
-9
1
y
o
-1
-2
-3
-4
-5
-10
在同一直角坐标系中画出函数y=- x2和y=-2x2的图像
1
2
函数y=- x2,y=-2x2的图像与函数y=-x2(图中虚线图形)的图像相比,有什么共同点和不同点 当a<0时,二次函数y=ax2的图像有什么特点
观察
共同点:
不同点:
开口向下;对称轴都是y轴;顶点都是原点,顶点是抛物线的低点
除顶点外,图像都在x轴下方
开口大小不同;a越大开口越大
y=-x2
1
2
1
2
3
4
5
x
-1
-2
-3
-4
-5
-6
-7
-8
-9
1
y
o
-1
-2
-3
-4
-5
-10
1
2
3
4
5
x
1
2
3
4
5
6
7
8
9
10
y
o
-1
-2
-3
-4
-5
一般地,抛物线y=ax2的对称轴是y轴,顶点是原点.
|a|越大,抛物线的开口越小
如果a>0时,抛物线的开口向上,顶点是抛物线的最低点在对称轴的左侧(当x<0时),y随着x的增大而减小。在对称轴的右侧(当x>0时),y随着x的增大而增大。
如果a<0时,抛物线的开口向下,顶点是抛物线的最高点在对称轴的左侧(当x<0时),y随着x的增大而增大。在对称轴的右侧(当x>0时),y随着x的增大而减小。
在同一坐标系内,抛物线y=ax2与抛物线y=-ax2是关于x轴对称的.
a>0
a<0
1、函数y=2x2的图象的开口 ,对称轴 ,顶点是 ;
2、函数y=-3x2的图象的开口 ,
对称轴 ,顶点是 。
向上
向下
y轴
y轴
(0,0)
(0,0)
3、抛物线 在x轴的 方(除顶点外),在对称轴的
左侧,y随着x的 ;在对称轴的右侧,y随着x的
,当x=0时,函数y的值最大,最大值是 ,
当x 0时,y<0.
下
增大而增大
增大而减小
0
4、已知抛物线y=ax2 (a ≠ 0),若点 A(-2,y1)与 B(3,y2)在此二次函数的图象上,则 y1___y2;(填“>”“=”或“<”)
请同学们把所学的二次函数图象的知识归纳小结。
y=ax2 顶点 对称轴 开口 图象 左侧 右侧
x y x y
a>0
a<0
增大
(0,0)
最低点
(0,0)
最高点
y轴
y轴
向上
向下
增大
减小
增大
增大
增大
减小
增大
课后作业
必做题:
教科书习题22.1
第3,4题.
你是雄鹰就要展翅翱翔!
同学们 再见
愿你们努力进取,永不言败!
致我亲爱的同学们
给我最大快乐的,
不是已懂的知识,
而是不断的学习.
----高斯
人教版义务教育教科书 数学 九年级(上册)
22.1 二次函数y=ax2的图象和性质
复习提问:
(1)一次函数的图象是一条_____.
直线
二次函数的图象是什么形 状呢?
x … -3 -2 -1 0 1 2 3 …
y=x2
画函数y=x2的图像
解: (1) 列表
… 9 4 1 0 1 4 9 …
(2) 描点
(3) 连线
1
2
3
4
5
x
1
2
3
4
5
6
7
8
9
10
y
o
-1
-2
-3
-4
-5
根据表中x,y的数值在坐标平面中描点(x,y),再用平滑曲线顺次连接各点,就得到y=x2的图像.
还记得如何用描点法画一个函数的图像吗
y=x2
我们把二次函数y=x2的图象的图象叫抛物线。实际上,二次函数的图象都是抛物线,它们的开口或者向上或者向下, 一般的二次函数y=ax2+bx+c的图象叫抛物线y=ax2+bx+c
抛物线 对称轴:y轴
顶点:(0,0)
任何一条抛物线y=ax2+bx+c都有对称轴和顶点。
这条抛物线关于
y轴对称,y轴就
是它的对称轴.
对称轴与抛物
线的交点叫做
抛物线的顶点.
x … -4 -3 -2 -1 0 1 2 3 4 …
y= x2
例1.在上面的直角坐标系中画出函数y= x2和y=2x2的图像。
解:(1) 列表
1
2
x … -2 -1.5 -1 -0.5 0 0.5 1 1.5 2 …
y=2x2
8
…
2
0.5
0
0.5
2
4.5
8
…
4.5
8
…
2
0.5
0
0.5
2
4.5
8
…
4.5
1
2
例1.在上面的直角坐标系中画出函数y= x2和y=2x2的图像。
解:(1) 列表
(2) 描点
(3) 连线
1
2
3
4
5
x
1
2
3
4
5
6
7
8
9
10
y
o
-1
-2
-3
-4
-5
1
2
函数y= x2,y=2x2的图像与函数y=x2(图中虚线图形)的图像相比,有什么共同点和不同点
当a>0时,二次函数y=ax2的图像有什么特点
观察
不同点:
共同点:开口向上;对称轴都是y轴;顶点都是原点,顶点是抛物线的最低点
除顶点外,图像都在x轴上方
开口大小不同,
1
2
x … -3 -2 -1 0 1 2 3 …
y=-x2
请画函数y=-x2的图像
解:(1) 列表
… -9 -4 -1 0 -1 -4 -9 …
(2) 描点
(3) 连线
根据表中x,y的数值在坐标平面中描点(x,y),再用平滑曲线顺次连接各点,就得到y=-x2的图像.
1
2
3
4
5
x
-1
-2
-3
-4
-5
-6
-7
-8
-9
1
y
o
-1
-2
-3
-4
-5
-10
y=-x2
1
2
3
4
5
x
1
2
3
4
5
6
7
8
9
10
y
o
-1
-2
-3
-4
-5
y=-x2
当a值相反时,两抛物线的
形状大小相同,开口相反
1
2
3
4
5
x
-1
-2
-3
-4
-5
-6
-7
-8
-9
1
y
o
-1
-2
-3
-4
-5
-10
在同一直角坐标系中画出函数y=- x2和y=-2x2的图像
1
2
函数y=- x2,y=-2x2的图像与函数y=-x2(图中虚线图形)的图像相比,有什么共同点和不同点 当a<0时,二次函数y=ax2的图像有什么特点
观察
共同点:
不同点:
开口向下;对称轴都是y轴;顶点都是原点,顶点是抛物线的低点
除顶点外,图像都在x轴下方
开口大小不同;a越大开口越大
y=-x2
1
2
1
2
3
4
5
x
-1
-2
-3
-4
-5
-6
-7
-8
-9
1
y
o
-1
-2
-3
-4
-5
-10
1
2
3
4
5
x
1
2
3
4
5
6
7
8
9
10
y
o
-1
-2
-3
-4
-5
一般地,抛物线y=ax2的对称轴是y轴,顶点是原点.
|a|越大,抛物线的开口越小
如果a>0时,抛物线的开口向上,顶点是抛物线的最低点在对称轴的左侧(当x<0时),y随着x的增大而减小。在对称轴的右侧(当x>0时),y随着x的增大而增大。
如果a<0时,抛物线的开口向下,顶点是抛物线的最高点在对称轴的左侧(当x<0时),y随着x的增大而增大。在对称轴的右侧(当x>0时),y随着x的增大而减小。
在同一坐标系内,抛物线y=ax2与抛物线y=-ax2是关于x轴对称的.
a>0
a<0
1、函数y=2x2的图象的开口 ,对称轴 ,顶点是 ;
2、函数y=-3x2的图象的开口 ,
对称轴 ,顶点是 。
向上
向下
y轴
y轴
(0,0)
(0,0)
3、抛物线 在x轴的 方(除顶点外),在对称轴的
左侧,y随着x的 ;在对称轴的右侧,y随着x的
,当x=0时,函数y的值最大,最大值是 ,
当x 0时,y<0.
下
增大而增大
增大而减小
0
4、已知抛物线y=ax2 (a ≠ 0),若点 A(-2,y1)与 B(3,y2)在此二次函数的图象上,则 y1___y2;(填“>”“=”或“<”)
请同学们把所学的二次函数图象的知识归纳小结。
y=ax2 顶点 对称轴 开口 图象 左侧 右侧
x y x y
a>0
a<0
增大
(0,0)
最低点
(0,0)
最高点
y轴
y轴
向上
向下
增大
减小
增大
增大
增大
减小
增大
课后作业
必做题:
教科书习题22.1
第3,4题.
你是雄鹰就要展翅翱翔!
同学们 再见
同课章节目录
