北京课改新版2021-2022学年八年级上册数学《第12章 三角形》单元测试卷(word版含解析)
文档属性
| 名称 | 北京课改新版2021-2022学年八年级上册数学《第12章 三角形》单元测试卷(word版含解析) |
|
|
| 格式 | zip | ||
| 文件大小 | 209.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北京课改版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-10-19 19:10:30 | ||
图片预览

文档简介
2021-2022学年北京课改新版八年级上册数学《第12章 三角形》单元测试卷
一.选择题
1.课堂上,老师把教学用的两块三角板叠放在一起,得到如图所示的图形,其中三角形的个数为( )
A.2 B.3 C.5 D.6
2.要使五边形木架(用五根根条钉成)不变形,至少要再钉上( )根本条.
A.1 B.2 C.3 D.4
3.如图,直线a∥b,在Rt△ABC中,点C在直线a上,若∠1=58°,∠2=24°,则∠A的度数为( )
A.56° B.34° C.36° D.24°
4.如图,工人师傅做了一个长方形窗框ABCD,E,F,G,H分别是四条边上的中点,为了使它稳固,需要在窗框上钉一根木条,这根木条不应钉在( )
A.A,C两点之间 B.G,H两点之间
C.B,F两点之间 D.E,G两点之间
5.在△ABC中,AD是BC边上中线,G是重心,若GD=6,那么AG的长为( )
A.9 B.12 C.3 D.2
6.如图,∠BAD=∠ADC=90°,以AD为一条高线的三角形个数有( )
A.2个 B.3个 C.4个 D.5个
7.如图所示的图形中,三角形共有( )
A.3个 B.4个 C.5个 D.6个
8.以下列数据为长度的三条线段,能组成三角形的是( )
A.2cm、3cm、5cm B.2cm、3cm、4cm
C.3cm、5cm、9cm D.8cm、4cm、4cm
9.如图,图中三角形的个数共有( )
A.3个 B.4个 C.5个 D.6个
10.如图,在直角△ABC中,∠CAB=90°,∠ABC=70°,AD是∠CAB的平分线,交边BC于点D,过点C作△ACD中AD边上的高线CE,则∠ECD的度数为( )
A.35° B.30° C.25° D.20°
二.填空题
11.三角形的三边之比是3:4:5,周长是36cm,则最长边比最短边长 .
12.如图,自行车的车身为三角结构,这样做根据的数学道理是 .
13.大桥钢架、索道支架、人字梁等为了坚固,都采用三角形结构,这是根据 .
14.已知点G是△ABC的重心,AG=4,那么点G与边BC中点的距离是 .
15.在△ABC中,AC=3cm,AD是△ABC中线,若△ABD周长比△ADC的周长大2cm,则BA= cm.
16.如图,共有 个三角形.
17.如图,在△ABC中,∠A=30°,∠B=50°,CD平分∠ACB,则∠ADC的度数是 .
18.若有一条公共边的两个三角形称为一对“共边三角形”,则图中以BC为公共边的“共边三角形”有 对.
19.三角形三边长分别为3,a,8,则a的取值范围是 .
20.如图,△ABC中,∠B=35°,∠BCA=75°,请依据尺规作图的作图痕迹,计算∠α= °
三.解答题
21.如图,已知==,△ABC的周长是14cm,求BC的长.
22.如图,G为△ABC重心,已知GA=5,GB=12,GC=13,求△ABC边AB上的高.
23.(1)下列图形中具有稳定性是 ;(只填图形序号)
(2)对不具有稳定性的图形,请适当地添加线段,使之具有稳定性.
24.如图所示,已知AD,AE分别是△ADC和△ABC的高和中线,AB=6cm,AC=8cm,BC=10cm,∠CAB=90°.试求:
(1)AD的长;
(2)△ABE的面积;
(3)△ACE和△ABE的周长的差.
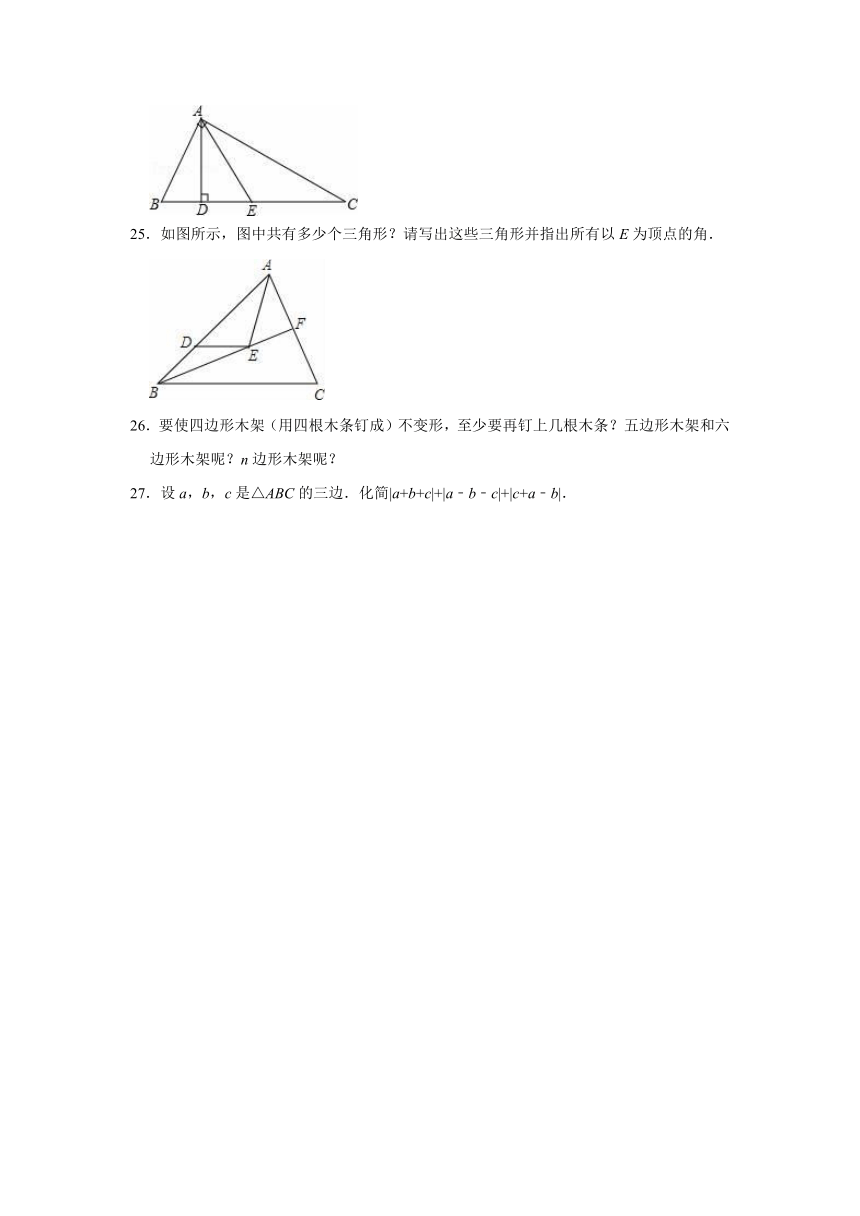
25.如图所示,图中共有多少个三角形?请写出这些三角形并指出所有以E为顶点的角.
26.要使四边形木架(用四根木条钉成)不变形,至少要再钉上几根木条?五边形木架和六边形木架呢?n边形木架呢?
27.设a,b,c是△ABC的三边.化简|a+b+c|+|a﹣b﹣c|+|c+a﹣b|.
参考答案与试题解析
一.选择题
1.解:图中三角形的个数是5个,
故选:C.
2.解:如图,至少需要2根木条.
故选:B.
3.解:如图,
∵∠1=54°,a∥b,
∴∠3=∠1=58°.
∵∠2=24°,∠A=∠3﹣∠2,
∴∠A=58°﹣24°=34°.
故选:B.
4.解:工人师傅做了一个长方形窗框ABCD,工人师傅为了使它稳固,需要在窗框上钉一根木条,这根木条不应钉在E、G两点之间(没有构成三角形),这种做法根据的是四边形没有稳定性.
故选:D.
5.解:如图,∵G是重心,
∴AG=2GD=12.
故选:B.
6.解:以AD为一条高线的三角形有△ADE、△ADC、△AEC、△DAB这4个,
故选:C.
7.解:三角形的个数有△BED,△AED,△ADC,△ABD,△ABC,
故选:C.
8.解:A、2+3=5,故不能组成三角形,不符合题意;
B、2+3>4,能组成三角形,符合题意;
C、3+5<9,不能组成三角形,不符合题意;
D、4+4=8,不能组成三角形,不符合题意.
故选:B.
9.解:图中是三角形的有:△AOC、△BOD、△AOB、△ABC、△ABD.
故选:C.
10.解:∵∠CAB=90°,AD是∠CAB的角平分线,
∴∠CAD=∠BAD=∠CAB=45°,
∵CE⊥AD,
∴∠ECA=∠CEA﹣∠CAE=45°,
∵∠BCA=∠CAB﹣∠B=20°,
∴∠ECD=∠ACE﹣∠BCA=25°,
故选:C.
二.填空题
11.解:由题意,设三边分别为3xcm,4xcm,5xcm,
则3x+4x+5x=36,
解得x=3,
三边分别为9cm,12cm,15cm.
故最长的边长比最短的边长长6cm.
故答案是:6cm.
12.解:自行车的车身为三角结构,这是因为三角形具有稳定性.
故答案为:三角形具有稳定性.
13.解:大桥钢架、索道支架、人字梁等为了坚固,都采用三角形结构,这是根据三角形具有稳定性.
故答案为:三角形具有稳定性.
14.解:如图,D是BC边的中点;
∵G是△ABC的重心,
∴AG=2GD=4,即GD=2,
故点G与边BC中点之间的距离是2,
故答案为:2.
15.解:∵AD是△ABC中线,
∴BD=CD,
∵△ABD周长比△ADC的周长大2cm,
∴(AB+BD+AD)﹣(AC+CD+AD)=2cm,
∴AB+BD+AD﹣AC﹣CD﹣AD=AB﹣AC=2cm.
∵AC=3cm,
∴BA=5cm.
故答案为:5.
16.解:图中有:△OAB,△OAC,△OAD,△OBC,△OCD,△OBD,共6个.
故答案为:6.
17.解:∵∠A=30°,∠B=50°,∠A+∠B+∠ACB=180°,
∴∠ACB=180°﹣30°﹣50°=100°,
∵CD平分∠ACB,
∴∠BCD=∠ACB=×100°=50°,
∴∠ADC=∠BCD+∠B=50°+50°=100°,
故答案为:100°.
18.解:△BDC与△BEC、△BDC与△BAC、△BEC与△BAC共三对.
故答案为:3.
19.解:∵三角形三边长分别为3,a,8,
∴8﹣3<a<8+3,
∴5<a<11.
故答案为:5<a<11.
20.解:∵∠B=35°,∠BCA=75°,
∴∠BAC=70°,
∵由作法可知,AD是∠BAC的平分线,
∴∠CAD=∠BAC=35°,
∵由作法可知,EF是线段BC的垂直平分线,
∴∠BCF=∠B=35°,
∵∠ACF=∠ACB﹣∠BCF=40°,
∴∠α=∠CAD+∠ACF=75°,
故答案为:75.
三.解答题
21.解:∵==,
设AB为5x,BD为2x,AC为5y,CD为2y,
∵△ABC的周长是14cm,
∴5x+2x+5y+2y=14,
解得:x+y=2,
所以BC=2(x+y)=4.
22.解:延长AG至E,使GD=DE,作CH⊥AB于点G.
∵G为△ABC重心,
∴AG=2GD=GE,BD=DC.
∴△BGD≌△CED(SAS).
∴∠BGE=∠GEC,EC=BG=12.
∵GC2=EG2+EC2,
∴∠BGE=∠GEC=90°.
∴S△ABD===45,
由勾股定理得
AB===13,
∴S△ABC=2S△ABD=90.
∴CH==.
23.解:(1)具有稳定性的是①④⑥三个.
(2)如图所示:
24.解:∵∠BAC=90°,AD是边BC上的高,
∴AB AC=BC AD,
∴AD===4.8(cm),即AD的长度为4.8cm;
(2)方法一:如图,∵△ABC是直角三角形,∠BAC=90°,AB=6cm,AC=8cm,
∴S△ABC=AB AC=×6×8=24(cm2).
又∵AE是边BC的中线,
∴BE=EC,
∴BE AD=EC AD,即S△ABE=S△AEC,
∴S△ABE=S△ABC=12(cm2).
∴△ABE的面积是12cm2.
方法二:因为BE=BC=5,由(1)知AD=4.8,
所以S△ABE=BE AD=×5×4.8=12(cm2).
∴△ABE的面积是12cm2.
(3)∵AE为BC边上的中线,
∴BE=CE,
∴△ACE的周长﹣△ABE的周长=AC+AE+CE﹣(AB+BE+AE)=AC﹣AB=8﹣6=2(cm),即△ACE和△ABE的周长的差是2cm.
25.解:图中共有7个,△AEF,△ADE,△DEB,△ABF,△BCF,△ABC,△ABE,以E为顶点的角是∠AEF,∠AED,∠DEB,∠DEF,∠AEB,∠BEF.
26.解:四边形木架,至少要再钉上1根木条,使四边形变成两个三角形;
五边形木架,至少要再钉上2根木条,使五边形变成3个三角形;
六边形木架,至少要再钉上3根木条,使六边形变成4个三角形;
n边形木架,至少要再钉上(n﹣3)根木条,使多边形变成(n﹣2)个三角形.
27.解:根据三角形的三边关系,两边之和大于第三边,
得a+b+c>0,a﹣b﹣c<0,c+a﹣b>0.
∴|a+b+c|+|a﹣b﹣c|+|c+a﹣b|
=a+b+c﹣a+b+c+c+a﹣b
=a+b+3c.
一.选择题
1.课堂上,老师把教学用的两块三角板叠放在一起,得到如图所示的图形,其中三角形的个数为( )
A.2 B.3 C.5 D.6
2.要使五边形木架(用五根根条钉成)不变形,至少要再钉上( )根本条.
A.1 B.2 C.3 D.4
3.如图,直线a∥b,在Rt△ABC中,点C在直线a上,若∠1=58°,∠2=24°,则∠A的度数为( )
A.56° B.34° C.36° D.24°
4.如图,工人师傅做了一个长方形窗框ABCD,E,F,G,H分别是四条边上的中点,为了使它稳固,需要在窗框上钉一根木条,这根木条不应钉在( )
A.A,C两点之间 B.G,H两点之间
C.B,F两点之间 D.E,G两点之间
5.在△ABC中,AD是BC边上中线,G是重心,若GD=6,那么AG的长为( )
A.9 B.12 C.3 D.2
6.如图,∠BAD=∠ADC=90°,以AD为一条高线的三角形个数有( )
A.2个 B.3个 C.4个 D.5个
7.如图所示的图形中,三角形共有( )
A.3个 B.4个 C.5个 D.6个
8.以下列数据为长度的三条线段,能组成三角形的是( )
A.2cm、3cm、5cm B.2cm、3cm、4cm
C.3cm、5cm、9cm D.8cm、4cm、4cm
9.如图,图中三角形的个数共有( )
A.3个 B.4个 C.5个 D.6个
10.如图,在直角△ABC中,∠CAB=90°,∠ABC=70°,AD是∠CAB的平分线,交边BC于点D,过点C作△ACD中AD边上的高线CE,则∠ECD的度数为( )
A.35° B.30° C.25° D.20°
二.填空题
11.三角形的三边之比是3:4:5,周长是36cm,则最长边比最短边长 .
12.如图,自行车的车身为三角结构,这样做根据的数学道理是 .
13.大桥钢架、索道支架、人字梁等为了坚固,都采用三角形结构,这是根据 .
14.已知点G是△ABC的重心,AG=4,那么点G与边BC中点的距离是 .
15.在△ABC中,AC=3cm,AD是△ABC中线,若△ABD周长比△ADC的周长大2cm,则BA= cm.
16.如图,共有 个三角形.
17.如图,在△ABC中,∠A=30°,∠B=50°,CD平分∠ACB,则∠ADC的度数是 .
18.若有一条公共边的两个三角形称为一对“共边三角形”,则图中以BC为公共边的“共边三角形”有 对.
19.三角形三边长分别为3,a,8,则a的取值范围是 .
20.如图,△ABC中,∠B=35°,∠BCA=75°,请依据尺规作图的作图痕迹,计算∠α= °
三.解答题
21.如图,已知==,△ABC的周长是14cm,求BC的长.
22.如图,G为△ABC重心,已知GA=5,GB=12,GC=13,求△ABC边AB上的高.
23.(1)下列图形中具有稳定性是 ;(只填图形序号)
(2)对不具有稳定性的图形,请适当地添加线段,使之具有稳定性.
24.如图所示,已知AD,AE分别是△ADC和△ABC的高和中线,AB=6cm,AC=8cm,BC=10cm,∠CAB=90°.试求:
(1)AD的长;
(2)△ABE的面积;
(3)△ACE和△ABE的周长的差.
25.如图所示,图中共有多少个三角形?请写出这些三角形并指出所有以E为顶点的角.
26.要使四边形木架(用四根木条钉成)不变形,至少要再钉上几根木条?五边形木架和六边形木架呢?n边形木架呢?
27.设a,b,c是△ABC的三边.化简|a+b+c|+|a﹣b﹣c|+|c+a﹣b|.
参考答案与试题解析
一.选择题
1.解:图中三角形的个数是5个,
故选:C.
2.解:如图,至少需要2根木条.
故选:B.
3.解:如图,
∵∠1=54°,a∥b,
∴∠3=∠1=58°.
∵∠2=24°,∠A=∠3﹣∠2,
∴∠A=58°﹣24°=34°.
故选:B.
4.解:工人师傅做了一个长方形窗框ABCD,工人师傅为了使它稳固,需要在窗框上钉一根木条,这根木条不应钉在E、G两点之间(没有构成三角形),这种做法根据的是四边形没有稳定性.
故选:D.
5.解:如图,∵G是重心,
∴AG=2GD=12.
故选:B.
6.解:以AD为一条高线的三角形有△ADE、△ADC、△AEC、△DAB这4个,
故选:C.
7.解:三角形的个数有△BED,△AED,△ADC,△ABD,△ABC,
故选:C.
8.解:A、2+3=5,故不能组成三角形,不符合题意;
B、2+3>4,能组成三角形,符合题意;
C、3+5<9,不能组成三角形,不符合题意;
D、4+4=8,不能组成三角形,不符合题意.
故选:B.
9.解:图中是三角形的有:△AOC、△BOD、△AOB、△ABC、△ABD.
故选:C.
10.解:∵∠CAB=90°,AD是∠CAB的角平分线,
∴∠CAD=∠BAD=∠CAB=45°,
∵CE⊥AD,
∴∠ECA=∠CEA﹣∠CAE=45°,
∵∠BCA=∠CAB﹣∠B=20°,
∴∠ECD=∠ACE﹣∠BCA=25°,
故选:C.
二.填空题
11.解:由题意,设三边分别为3xcm,4xcm,5xcm,
则3x+4x+5x=36,
解得x=3,
三边分别为9cm,12cm,15cm.
故最长的边长比最短的边长长6cm.
故答案是:6cm.
12.解:自行车的车身为三角结构,这是因为三角形具有稳定性.
故答案为:三角形具有稳定性.
13.解:大桥钢架、索道支架、人字梁等为了坚固,都采用三角形结构,这是根据三角形具有稳定性.
故答案为:三角形具有稳定性.
14.解:如图,D是BC边的中点;
∵G是△ABC的重心,
∴AG=2GD=4,即GD=2,
故点G与边BC中点之间的距离是2,
故答案为:2.
15.解:∵AD是△ABC中线,
∴BD=CD,
∵△ABD周长比△ADC的周长大2cm,
∴(AB+BD+AD)﹣(AC+CD+AD)=2cm,
∴AB+BD+AD﹣AC﹣CD﹣AD=AB﹣AC=2cm.
∵AC=3cm,
∴BA=5cm.
故答案为:5.
16.解:图中有:△OAB,△OAC,△OAD,△OBC,△OCD,△OBD,共6个.
故答案为:6.
17.解:∵∠A=30°,∠B=50°,∠A+∠B+∠ACB=180°,
∴∠ACB=180°﹣30°﹣50°=100°,
∵CD平分∠ACB,
∴∠BCD=∠ACB=×100°=50°,
∴∠ADC=∠BCD+∠B=50°+50°=100°,
故答案为:100°.
18.解:△BDC与△BEC、△BDC与△BAC、△BEC与△BAC共三对.
故答案为:3.
19.解:∵三角形三边长分别为3,a,8,
∴8﹣3<a<8+3,
∴5<a<11.
故答案为:5<a<11.
20.解:∵∠B=35°,∠BCA=75°,
∴∠BAC=70°,
∵由作法可知,AD是∠BAC的平分线,
∴∠CAD=∠BAC=35°,
∵由作法可知,EF是线段BC的垂直平分线,
∴∠BCF=∠B=35°,
∵∠ACF=∠ACB﹣∠BCF=40°,
∴∠α=∠CAD+∠ACF=75°,
故答案为:75.
三.解答题
21.解:∵==,
设AB为5x,BD为2x,AC为5y,CD为2y,
∵△ABC的周长是14cm,
∴5x+2x+5y+2y=14,
解得:x+y=2,
所以BC=2(x+y)=4.
22.解:延长AG至E,使GD=DE,作CH⊥AB于点G.
∵G为△ABC重心,
∴AG=2GD=GE,BD=DC.
∴△BGD≌△CED(SAS).
∴∠BGE=∠GEC,EC=BG=12.
∵GC2=EG2+EC2,
∴∠BGE=∠GEC=90°.
∴S△ABD===45,
由勾股定理得
AB===13,
∴S△ABC=2S△ABD=90.
∴CH==.
23.解:(1)具有稳定性的是①④⑥三个.
(2)如图所示:
24.解:∵∠BAC=90°,AD是边BC上的高,
∴AB AC=BC AD,
∴AD===4.8(cm),即AD的长度为4.8cm;
(2)方法一:如图,∵△ABC是直角三角形,∠BAC=90°,AB=6cm,AC=8cm,
∴S△ABC=AB AC=×6×8=24(cm2).
又∵AE是边BC的中线,
∴BE=EC,
∴BE AD=EC AD,即S△ABE=S△AEC,
∴S△ABE=S△ABC=12(cm2).
∴△ABE的面积是12cm2.
方法二:因为BE=BC=5,由(1)知AD=4.8,
所以S△ABE=BE AD=×5×4.8=12(cm2).
∴△ABE的面积是12cm2.
(3)∵AE为BC边上的中线,
∴BE=CE,
∴△ACE的周长﹣△ABE的周长=AC+AE+CE﹣(AB+BE+AE)=AC﹣AB=8﹣6=2(cm),即△ACE和△ABE的周长的差是2cm.
25.解:图中共有7个,△AEF,△ADE,△DEB,△ABF,△BCF,△ABC,△ABE,以E为顶点的角是∠AEF,∠AED,∠DEB,∠DEF,∠AEB,∠BEF.
26.解:四边形木架,至少要再钉上1根木条,使四边形变成两个三角形;
五边形木架,至少要再钉上2根木条,使五边形变成3个三角形;
六边形木架,至少要再钉上3根木条,使六边形变成4个三角形;
n边形木架,至少要再钉上(n﹣3)根木条,使多边形变成(n﹣2)个三角形.
27.解:根据三角形的三边关系,两边之和大于第三边,
得a+b+c>0,a﹣b﹣c<0,c+a﹣b>0.
∴|a+b+c|+|a﹣b﹣c|+|c+a﹣b|
=a+b+c﹣a+b+c+c+a﹣b
=a+b+3c.
同课章节目录
- 第十章 分式
- 10.1 分式
- 10.2 分式的基本性质
- 10.3 分式的乘除法
- 10.4 分式的加减法
- 10.5 可化为一元一次方程的分式方程及其应用
- 第十一章 实数和二次根式
- 11.1 平方根
- 11.2 立方根
- 11.3 用科学计算器开方
- 11.4 无理数与实数
- 11.5 二次根式及其性质
- 11.6 二次根式的乘除法
- 11.7 二次根式的加减法
- 第十二章 三角形
- 12.1 三角形
- 12.2 三角形的性质
- 12.3 三角形中的主要线段
- 12.4 全等三角形
- 12.5 全等三角形的判定
- 12.6 等腰三角形
- 12.7 直角三角形
- 12.8 基本作图
- 12.9 逆命题 、逆定理
- 12.10 轴对称和轴对称图形
- 12.11 勾股定理
- 12.12 勾股定理的逆定理
- 第十三章 事件与可能性
- 13.1 必然事件与随机事件
- 13.2 随机事件发生的可能性
- 13.3 求简单随机事件发生的可能性的大小
