黑龙江省大庆市第69中学2011-2012年度下学期九年级数学期末试卷
文档属性
| 名称 | 黑龙江省大庆市第69中学2011-2012年度下学期九年级数学期末试卷 |
|
|
| 格式 | zip | ||
| 文件大小 | 119.1KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版(五四学制) | ||
| 科目 | 数学 | ||
| 更新时间 | 2012-08-21 00:00:00 | ||
图片预览


文档简介
大庆市第69中学初三年级数学期末试卷
考试时间:2012年7月11日 答卷时间:120分钟 卷面分值:120分
一、填空(每空3分,共33分)
1. 在Rt△ABC中,∠C=90°,sinA=,则∠A=____________.
2. 抛物线y=x2-x的顶点坐标是_________________.
3. 若反比例函数y=(2k-1)的图像经过二、四象限,则k=___________.
4. 已知y-2比x成反比例,当x=3时,y=1, 则y与x间的函数关系式为______________.
5. 在Rt△ABC中,∠C=90°,tanA=,则sinB=____________.
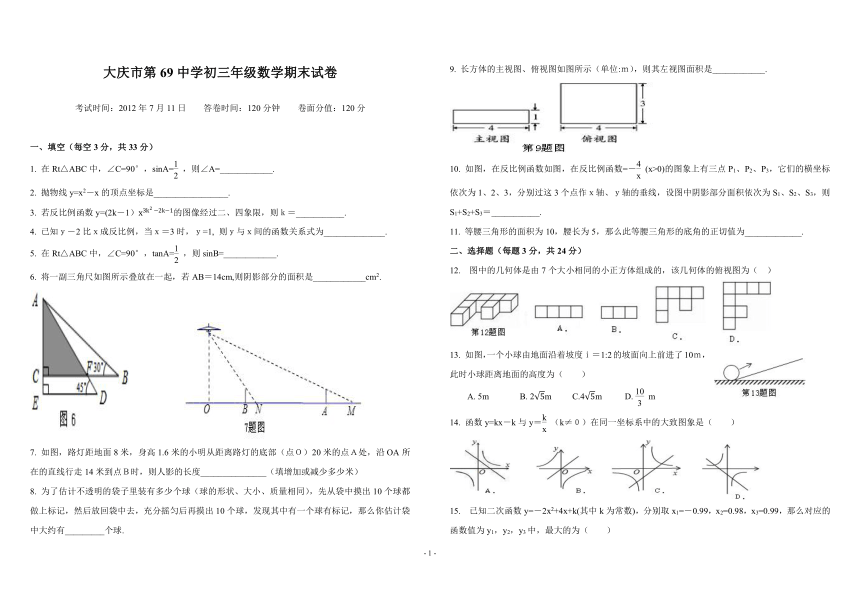
6. 将一副三角尺如图所示叠放在一起,若AB=14cm,则阴影部分的面积是____________cm2.
7. 如图,路灯距地面8米,身高1.6米的小明从距离路灯的底部(点O)20米的点A处,沿OA所在的直线行走14米到点B时,则人影的长度_______________(填增加或减少多少米)
8. 为了估计不透明的袋子里装有多少个球(球的形状、大小、质量相同),先从袋中摸出10个球都做上标记,然后放回袋中去,充分摇匀后再摸出10个球,发现其中有一个球有标记,那么你估计袋中大约有_________个球.
9. 长方体的主视图、俯视图如图所示(单位:m),则其左视图面积是____________.
10. 如图,在反比例函数如图,在反比例函数=-(x>0)的图象上有三点P1、P2、P3,它们的横坐标依次为1、2、3,分别过这3个点作x轴、y轴的垂线,设图中阴影部分面积依次为S1、S2、S3,则S1+S2+S3=___________.
11. 等腰三角形的面积为10,腰长为5,那么此等腰三角形的底角的正切值为_____________.
二、选择题(每题3分,共24分)
12. 图中的几何体是由7个大小相同的小正方体组成的,该几何体的俯视图为( )
13. 如图,一个小球由地面沿着坡度i=1:2的坡面向上前进了10m,此时小球距离地面的高度为( )
A. 5m B. 2m C.4m D. m
14. 函数y=kx-k与y=(k≠0)在同一坐标系中的大致图象是( )
15. 已知二次函数y=-2x2+4x+k(其中k为常数),分别取x1=-0.99,x2=0.98,x3=0.99,那么对应的函数值为y1,y2,y3中,最大的为( )
A. y3 B.y2, C. y1, D.不能确定,与k的取值有关
16. 无论m为任何实数,二次函数y=x2+(2-m)x+m的图象总通过的点( )
A.(1,3) B.(1,0) C.(-1,3) D.(-1,0)
17. 在围棋盒中有x颗白色棋子和y颗黑色棋子,从盒中随机取出一颗棋子,取得白色棋子的概率是,如再往盒中放进3颗黑色棋子,取得白色棋子的概率变为,则原来盒里有白色棋子( ) A.1颗 B.2颗 C.3颗 D.4颗
18. 已知反比例函数y=的图象上有两点A(x1,y1),B(x2,y2),且x1A.正数 B.负数 C.非负数 D.不能确定
19.如图,过边长为1的等边△ABC的边AB上一点P,作PE⊥AC于E,Q为BC延长线上一点,当PA=CQ时,连PQ交AC边于D,则DE的长为( )
A. B. C. D.不能确定
三、解答下列各题:
20. 计算:(每题5分,共10分)
(1) - tan45° (2)6tan230°-sin60°+2tan45°
21.(8分)某中学学生会为考察该校学生参加课外体育活动的情况,采取抽样调查的方法从篮球、排球、乒乓球、足球及其他等五个方面调查了若干名学生的兴趣爱好(每人只能选其中一项),并将调查结果绘制成如下两幅不完整的统计图,请根据图中提供的信息解答下列问题:
(1)在这次考察中一共调查了多少名学生?
(2)在扇形统计图中,“乒乓球”部分所对应的圆心角是多少度?
(3)补全条形统计图;
(4)若全校有1500名学生,试估计该校喜欢篮球的学生约有多少人?
22.(9分)小英和小丽用两个转盘做“配紫色”游戏,配成紫色小英得1分,否则小丽得1分,这个游戏对双方公平吗?请用树状图法或列表法分析(红色+蓝色=紫色)
23.(9分)在数学活动课上,九年级(1)班数学兴趣小组的同学们测量校园内一棵大树的高度,设计的测量方案及数据如下:
(1)在大树前的平地上选择一点A,测得由点A看大树顶端C的仰角为30°;
(2)在点A和大树之间选择一点B(A、B、D在同一直线上),测得由点B看大树顶端C的仰角恰好为45°;
(3)量出A、B间的距离为4米.请你根据以上数据求出大树CD的高度.
(精确到0.1,参考数据: ≈1.41 ,≈1.73)
24.(9分)如图,在Rt△ABC中,∠C=90°,sinB=,点D在BC上且∠ADC=45°,DC=6,求∠BAD的正切值。
25.(9分)如图,直线y=k1x+b与反比例函数y=的图象交于A(1,6)、B(a,3)两点.
(1)求k1、k2的值;
(2)直接写出k1x+b->0时的x的取值范围;
(3)如图,等腰梯形OBCD中,BC∥OD,OB=CD,OD边在x轴上,过点C作CE⊥OD于点E,CE和反比例函数的图象交于点P,当梯形OBCD的面积为12时,请判断PC和PE的大小关系,并说明理由.
26.(9分)已知:如图,抛物线y=ax2-2ax+c(a0)与y轴交于点C(0,4),与x轴交于点A、B,点A的坐标为(4,0).
(1)求该抛物线的解析式;
(2)点Q是线段AB上的动点,过点Q作QE∥AC,交BC于点E,连接CQ.当△CQE的面积最大时,求点Q的坐标;
(3)若平行于x轴的动直线l与该抛物线交于点P,与直线AC交于点F,点D的坐标为(2,0).问:是否存在这样的直线l,使得△ODF是等腰三角形?若存在,请求出点P的坐标;若不存在,请说明理由.
(备用图)
- 1 -
考试时间:2012年7月11日 答卷时间:120分钟 卷面分值:120分
一、填空(每空3分,共33分)
1. 在Rt△ABC中,∠C=90°,sinA=,则∠A=____________.
2. 抛物线y=x2-x的顶点坐标是_________________.
3. 若反比例函数y=(2k-1)的图像经过二、四象限,则k=___________.
4. 已知y-2比x成反比例,当x=3时,y=1, 则y与x间的函数关系式为______________.
5. 在Rt△ABC中,∠C=90°,tanA=,则sinB=____________.
6. 将一副三角尺如图所示叠放在一起,若AB=14cm,则阴影部分的面积是____________cm2.
7. 如图,路灯距地面8米,身高1.6米的小明从距离路灯的底部(点O)20米的点A处,沿OA所在的直线行走14米到点B时,则人影的长度_______________(填增加或减少多少米)
8. 为了估计不透明的袋子里装有多少个球(球的形状、大小、质量相同),先从袋中摸出10个球都做上标记,然后放回袋中去,充分摇匀后再摸出10个球,发现其中有一个球有标记,那么你估计袋中大约有_________个球.
9. 长方体的主视图、俯视图如图所示(单位:m),则其左视图面积是____________.
10. 如图,在反比例函数如图,在反比例函数=-(x>0)的图象上有三点P1、P2、P3,它们的横坐标依次为1、2、3,分别过这3个点作x轴、y轴的垂线,设图中阴影部分面积依次为S1、S2、S3,则S1+S2+S3=___________.
11. 等腰三角形的面积为10,腰长为5,那么此等腰三角形的底角的正切值为_____________.
二、选择题(每题3分,共24分)
12. 图中的几何体是由7个大小相同的小正方体组成的,该几何体的俯视图为( )
13. 如图,一个小球由地面沿着坡度i=1:2的坡面向上前进了10m,此时小球距离地面的高度为( )
A. 5m B. 2m C.4m D. m
14. 函数y=kx-k与y=(k≠0)在同一坐标系中的大致图象是( )
15. 已知二次函数y=-2x2+4x+k(其中k为常数),分别取x1=-0.99,x2=0.98,x3=0.99,那么对应的函数值为y1,y2,y3中,最大的为( )
A. y3 B.y2, C. y1, D.不能确定,与k的取值有关
16. 无论m为任何实数,二次函数y=x2+(2-m)x+m的图象总通过的点( )
A.(1,3) B.(1,0) C.(-1,3) D.(-1,0)
17. 在围棋盒中有x颗白色棋子和y颗黑色棋子,从盒中随机取出一颗棋子,取得白色棋子的概率是,如再往盒中放进3颗黑色棋子,取得白色棋子的概率变为,则原来盒里有白色棋子( ) A.1颗 B.2颗 C.3颗 D.4颗
18. 已知反比例函数y=的图象上有两点A(x1,y1),B(x2,y2),且x1
19.如图,过边长为1的等边△ABC的边AB上一点P,作PE⊥AC于E,Q为BC延长线上一点,当PA=CQ时,连PQ交AC边于D,则DE的长为( )
A. B. C. D.不能确定
三、解答下列各题:
20. 计算:(每题5分,共10分)
(1) - tan45° (2)6tan230°-sin60°+2tan45°
21.(8分)某中学学生会为考察该校学生参加课外体育活动的情况,采取抽样调查的方法从篮球、排球、乒乓球、足球及其他等五个方面调查了若干名学生的兴趣爱好(每人只能选其中一项),并将调查结果绘制成如下两幅不完整的统计图,请根据图中提供的信息解答下列问题:
(1)在这次考察中一共调查了多少名学生?
(2)在扇形统计图中,“乒乓球”部分所对应的圆心角是多少度?
(3)补全条形统计图;
(4)若全校有1500名学生,试估计该校喜欢篮球的学生约有多少人?
22.(9分)小英和小丽用两个转盘做“配紫色”游戏,配成紫色小英得1分,否则小丽得1分,这个游戏对双方公平吗?请用树状图法或列表法分析(红色+蓝色=紫色)
23.(9分)在数学活动课上,九年级(1)班数学兴趣小组的同学们测量校园内一棵大树的高度,设计的测量方案及数据如下:
(1)在大树前的平地上选择一点A,测得由点A看大树顶端C的仰角为30°;
(2)在点A和大树之间选择一点B(A、B、D在同一直线上),测得由点B看大树顶端C的仰角恰好为45°;
(3)量出A、B间的距离为4米.请你根据以上数据求出大树CD的高度.
(精确到0.1,参考数据: ≈1.41 ,≈1.73)
24.(9分)如图,在Rt△ABC中,∠C=90°,sinB=,点D在BC上且∠ADC=45°,DC=6,求∠BAD的正切值。
25.(9分)如图,直线y=k1x+b与反比例函数y=的图象交于A(1,6)、B(a,3)两点.
(1)求k1、k2的值;
(2)直接写出k1x+b->0时的x的取值范围;
(3)如图,等腰梯形OBCD中,BC∥OD,OB=CD,OD边在x轴上,过点C作CE⊥OD于点E,CE和反比例函数的图象交于点P,当梯形OBCD的面积为12时,请判断PC和PE的大小关系,并说明理由.
26.(9分)已知:如图,抛物线y=ax2-2ax+c(a0)与y轴交于点C(0,4),与x轴交于点A、B,点A的坐标为(4,0).
(1)求该抛物线的解析式;
(2)点Q是线段AB上的动点,过点Q作QE∥AC,交BC于点E,连接CQ.当△CQE的面积最大时,求点Q的坐标;
(3)若平行于x轴的动直线l与该抛物线交于点P,与直线AC交于点F,点D的坐标为(2,0).问:是否存在这样的直线l,使得△ODF是等腰三角形?若存在,请求出点P的坐标;若不存在,请说明理由.
(备用图)
- 1 -
同课章节目录
