3.4二次函数y=ax2 bx c的图象与性质 优生辅导测评 2021-2022学年鲁教版(五四制)九年级数学上册(word版含答案)
文档属性
| 名称 | 3.4二次函数y=ax2 bx c的图象与性质 优生辅导测评 2021-2022学年鲁教版(五四制)九年级数学上册(word版含答案) |  | |
| 格式 | doc | ||
| 文件大小 | 343.9KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 鲁教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-10-20 07:06:29 | ||
图片预览




文档简介
2021-2022年鲁教版九年级数学上册《3.4二次函数y=ax2+bx+c的图象与性质》
优生辅导测评(附答案)
一.选择题(共11小题,满分33分)
1.二次函数y=ax2+4ax+1﹣a的图象只过三个象限,则a的取值范围为( )
A.<a≤1 B.0<a< C.﹣1<a<0 D.a<﹣1
2.在同一平面直角坐标系中,函数y=mx+m和函数y=﹣mx2+2x+2(m是常数,且m≠0)的图象可能是( )
A.B.C.D.
3.对称轴为直线x=1的抛物线y=ax2+bx+c(a、b、c为常数,且a≠0)如图所示,小明同学得出了以下结论:①abc<0,②b2>4ac,③4a+2b+c>0,④3a+c>0,⑤(a+c)2<b2.其中结论正确的为( )
A.①②④ B.②③⑤ C.②④⑤ D.②③④
4.二次函数y=ax2+bx+c(a≠0)的部分图象如图所示,有以下结论:①a﹣b+c<0;②abc>0;③2a﹣b<0;④3a+c=0;⑤>4a,其中正确的个数为( )
A.1个 B.2个 C.3个 D.4个
5.二次函数y=ax2+bx+c(a≠0)的图象如图所示.下列结论:①abc>0;②2a+b=0;③m为任意实数,则a+b>am2+bm;④a﹣b+c>0;⑤若ax12+bx1=ax22+bx2且x1≠x2,则x1+x2=2.其中正确的有( )
A.①④ B.③④ C.②⑤ D.②③⑤
6.二次函数y=ax2+bx+c(a≠0)的图象如图,给出下列四个结论:
①3a+2b+c<0;
②3a+c<b2﹣4ac;
③方程2ax2+2bx+2c﹣5=0没有实数根;
④m(am+b)+b<a(m≠﹣1).
其中正确结论的个数是( )
A.4个 B.3个 C.2个 D.1个
7.已知点A(x1.y1),B(x2、y2),C(x3、y3)都在二次函数y=ax2(a<0)的图象上.且x1<x2<0<x3,则下列结论可能成立的是( )
A.y1<y2<y3<0 B.0<y1<y2<y3 C.y1<y2<0<y3 D.y3<y2<y1<0
8.如图,在△ABC中,∠B=90°,AB=4cm,BC=8cm.动点P从点A出发,沿边AB向点B以1cm/s的速度移动(不与点B重合),同时动点Q从点B出发,沿边BC向点C以2cm/s的速度移动(不与点C重合).当四边形APQC的面积最小时,经过的时间为( )
A.1s B.2s C.3s D.4s
9.如图,将抛物线y=(x﹣1)2的图象位于直线y=4以上的部分向下翻折,得到新的图象(实线部分),若直线y=﹣x+m与新图象只有四个交点,求m的取值范围.( )
A.<m<3 B.<m<7 C.<m<7 D.<m<3
10.二次函数y=ax2+bx+c的图象如图所示,对称轴是直线x=1.下列结论:①abc<0;②3a+c>0;③(a+c)2﹣b2<0;④a+b≤m(am+b)(m为实数).其中结论正确的个数为( )
A.1个 B.2个 C.3个 D.4个
11.如果抛物线y=x2﹣6x+c﹣2的顶点到x轴的距离是3,那么c的值等于( )
A.8 B.14 C.8或14 D.﹣8或﹣14
二.填空题(共10小题,满分30分)
12.已知二次函数y=﹣(x+k)2+h,当x>﹣2时,y随x的增大而减小,则k的取值范围是 .
13.已知二次函数y=mx2+2mx+1(m≠0)在﹣2≤x≤2时有最小值﹣2,则m= .
14.二次函数y=x2﹣2x﹣3(3≤x≤6)的最小值是 .
15.已知二次函数y=x2+2mx+1,若x>1时,y随x的增大而增大,则m的取值范围是 .
16.将二次函数y=x2﹣4x﹣4的图象先向上平移3个单位长度,再向右平移2个单位长度得到的图象对应的二次函数的解析式为y=x2+ax+b,则ab= .
17.二次函数y=(x﹣1)2+1的图象先向右平移2个单位,再向上平移3个单位,平移后图象的函数表达式为 .
18.将二次函数y=2x2﹣4x﹣1的图象沿着y轴翻折,所得到的图象对应的函数表达式是 .
19.若二次函数y=﹣x2+mx在﹣1≤x≤2时的最大值为3,那么m的值是 .
20.抛物线y=2x2﹣4x+3绕坐标原点旋转180°所得的抛物线的解析式是 .
21.用一根长为32cm的铁丝围成一个矩形,则围成矩形面积的最大值是 cm2.
三.解答题(共10小题,满分57分)
22.已知二次函数y=﹣x2+2tx﹣t+1(是常数).
(1)求此函数的顶点坐标.(用含t的代数式表示)
(2)当x≥2时,y随x的增大而减小,求t的取值范围.
(3)当0≤x≤1时,该函数有最大值4,求t的值.
23.已知二次函数y=﹣x2+2kx+1﹣k(k是常数)
(1)求此函数的顶点坐标.
(2)当x≥1时,y随x的增大而减小,求k的取值范围.
(3)当0≤x≤1时,该函数有最大值3,求k的值.
24.已知二次函数y=﹣2x2,y=﹣2(x﹣2)2,y=﹣2(x﹣2)2+2,请回答下列问题:
(1)写出抛物线y=﹣2(x﹣2)2的顶点坐标,开口方向和对称轴;
(2)分别通过怎样的平移,可以由抛物线y=﹣2x2得到抛物线y=﹣2(x﹣2)2和y=﹣2(x﹣2)2+2?
(3)如果要得到抛物线y=﹣2(x﹣2017)2﹣2018,应将y=﹣2x2怎样平移?
25.函数y=(m+2)是关于x的二次函数,求:
(1)满足条件的m值;
(2)m为何值时,抛物线有最低点?求出这个最低点.这时,当x为何值时,y随x的增大而增大?
(3)m为何值时,函数有最大值?最大值是多少?这时,当x为何值时,y随x的增大而减小.
26.如图,平面直角坐标系中,抛物线y=﹣x2+4x+m﹣4(m为常数)与y轴的交点为C,M(3,0)与N(0,﹣2)分别是x轴、y轴上的点
(1)当m=1时,求抛物线顶点坐标.
(2)若3≤x≤3+m时,函数y=﹣x2+4x+m﹣4有最小值﹣7,求m的值.
(3)若抛物线与线段MN有公共点,直接写出m的取值范围是 .
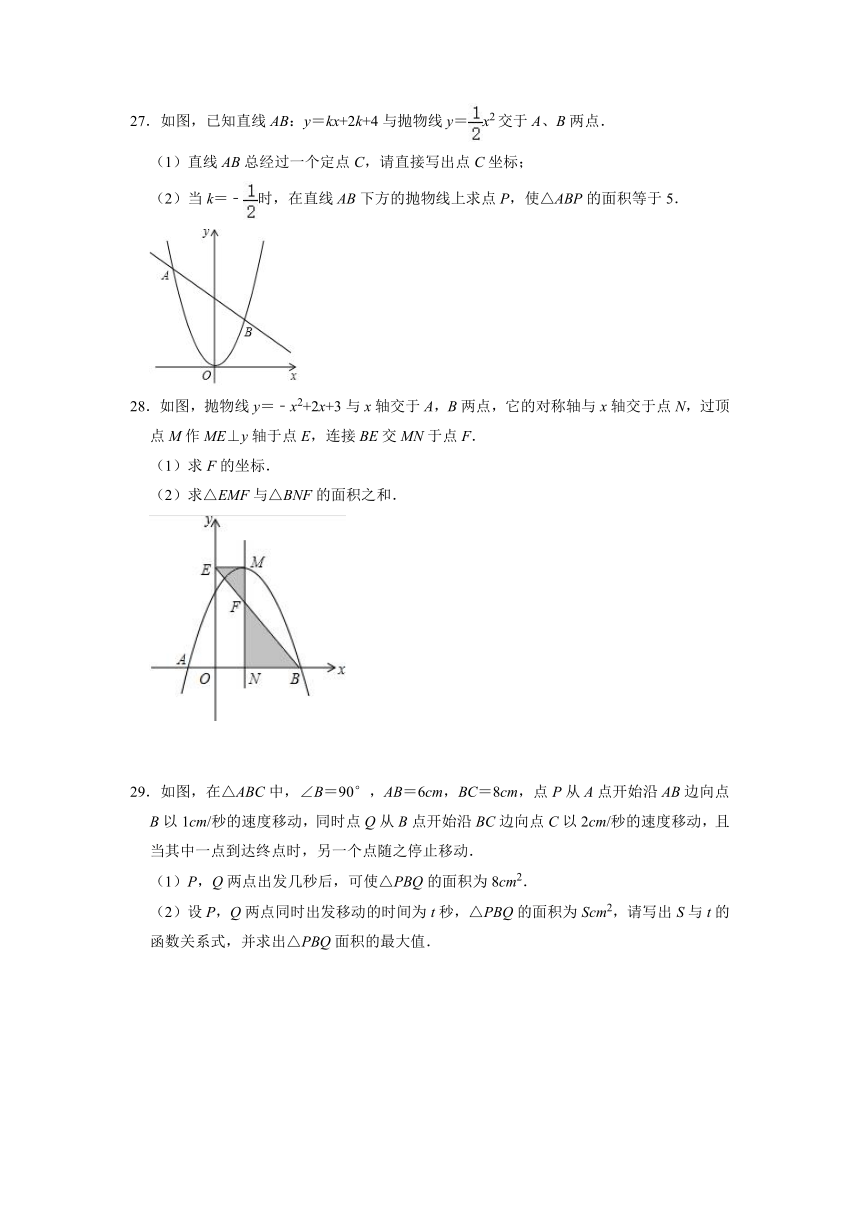
27.如图,已知直线AB:y=kx+2k+4与抛物线y=x2交于A、B两点.
(1)直线AB总经过一个定点C,请直接写出点C坐标;
(2)当k=﹣时,在直线AB下方的抛物线上求点P,使△ABP的面积等于5.
28.如图,抛物线y=﹣x2+2x+3与x轴交于A,B两点,它的对称轴与x轴交于点N,过顶点M作ME⊥y轴于点E,连接BE交MN于点F.
(1)求F的坐标.
(2)求△EMF与△BNF的面积之和.
29.如图,在△ABC中,∠B=90°,AB=6cm,BC=8cm,点P从A点开始沿AB边向点B以1cm/秒的速度移动,同时点Q从B点开始沿BC边向点C以2cm/秒的速度移动,且当其中一点到达终点时,另一个点随之停止移动.
(1)P,Q两点出发几秒后,可使△PBQ的面积为8cm2.
(2)设P,Q两点同时出发移动的时间为t秒,△PBQ的面积为Scm2,请写出S与t的函数关系式,并求出△PBQ面积的最大值.
30.已知抛物线C1的解析式是y=2x2﹣4x+5,抛物线C2与抛物线C1关于x轴对称,求抛物线C2的解析式.
31.如图.抛物线y=ax2+bx+与直线AB交于点A(﹣1,0),B(4,),点D是抛物线上位于直线AB上方的一点(不与点A,B重合),连接AD,BD.
(1)求抛物线的解析;
(2)设△ADB的面为S,求出当S取最大值时的点D的坐标.
参考答案
一.选择题(共11小题,满分33分)
1.解:∵抛物线的对称轴为直线x=﹣=﹣2,抛物线图象只过三个象限,
∴当a>0,抛物线经过第一、二、三象限,当a<0,抛物线经过第二、三、四象限
∴当a>0时,,解得<a≤1;
当a<0时,,无解,
所以a的范围为<a≤1;
故选:A.
2.解:A、由函数y=mx+m的图象可知m<0,即函数y=﹣mx2+2x+2开口方向朝上,与图象不符,故A选项错误;
B、由函数y=mx+m的图象可知m<0,对称轴为x=﹣=﹣=<0,则对称轴应在y轴左侧,与图象不符,故B选项错误;
C、由函数y=mx+m的图象可知m>0,即函数y=﹣mx2+2x+2开口方向朝下,与图象不符,故C选项错误;
D、由函数y=mx+m的图象可知m<0,即函数y=﹣mx2+2x+2开口方向朝上,对称轴为x=﹣=﹣=<0,则对称轴应在y轴左侧,与图象相符,故D选项正确;
故选:D.
3.解:①由图象可知:a>0,c<0,
∵﹣=1,
∴b=﹣2a<0,
∴abc>0,故①错误;
②∵抛物线与x轴有两个交点,
∴b2﹣4ac>0,
∴b2>4ac,故②正确;
③当x=2时,y=4a+2b+c<0,故③错误;
④当x=﹣1时,y=a﹣b+c=a﹣(﹣2a)+c>0,
∴3a+c>0,故④正确;
⑤当x=﹣1时,y>0,即:a﹣b+c>0.
当x=1时,y<0,即:a+b+c<0
两式相乘得(a+c)2﹣b2<0,
∴(a+c)2<b2.故⑤正确.
故选:C.
4.解:由图象可知,当x=﹣1时,y=a﹣b+c>0,
∴①不合题意,
∵抛物线的开口向下,
∴a<0,
∵抛物线与y轴的交点在x轴的上方,
∴c>0,
∵抛物线的对称轴为x=﹣1,
∴,即b=2a,
∴b<0,
∴abc>0,
∴②符合题意,
∵抛物线的对称轴为x=﹣1,
∴,即b=2a,
∴2a﹣b=0,
∴③不合题意,
由图象可知,抛物线与x轴的另一个交点为(1,0),
∴当x=1时,y=a+b+c=a+2a+c=3a+c=0,
∴④符合题意,
∵,
∴,
∴⑤符合题意,
∴符合题意的有三个,
故选:C.
5.解:①抛物线开口方向向下,则a<0.
抛物线对称轴位于y轴右侧,则a、b异号,即ab<0.
抛物线与y轴交于正半轴,则c>0.
所以abc<0.
故①错误.
②∵抛物线对称轴为直线x==1,
∴b=﹣2a,即2a+b=0,
故②正确;
③∵抛物线对称轴为直线x=1,
∴函数的最大值为:a+b+c,
∴a+b+c≥am2+bm+c,即a+b≥am2+bm,
故③错误;
④∵抛物线与x轴的一个交点在(3,0)的左侧,而对称轴为直线x=1,
∴抛物线与x轴的另一个交点在(﹣1,0)的右侧
∴当x=﹣1时,y<0,
∴a﹣b+c<0,
故④错误;
⑤∵ax12+bx1=ax22+bx2,
∴ax12+bx1﹣ax22﹣bx2=0,
∴a(x1+x2)(x1﹣x2)+b(x1﹣x2)=0,
∴(x1﹣x2)[a(x1+x2)+b]=0,
而x1≠x2,
∴a(x1+x2)+b=0,即x1+x2=,
∵b=﹣2a,
∴x1+x2=2,
故⑤正确.
综上所述,正确的有②⑤.
故选:C.
6.解:由图象可知,当x=1时,y<0,即a+b+c<0,
∵对称轴x=﹣=﹣1,a<0,
∴b=2a<0,
∴a+2a+c<0,即3a+c<0,
∴3a+2b+c<0,故①正确;
∵抛物线与x轴有两个交点,
∴b2﹣4ac>0,
∴3a+c<0<b2﹣4ac,故②正确;
∵2ax2+2bx+2c﹣5=0,
∴ax2+bx+c=,
结合图象可知,不能确定抛物线y=ax2+bx+c与直线y=的交点情况,
故③不正确;
∵当x=m(m≠﹣1)时,y=am2+bm+c,且当x=﹣1时,函数y取得最大值,
∴a﹣b+c>am2+bm+c,
∴m(am+b)+b<a,故④正确;
综上,正确结论有①②④共3个,
故选:B.
7.解:∵二次函数y=ax2的对称轴为y轴,开口向下,且关于y轴对称,
∴x<0时,y随x的增大而增大,
∵x1<x2<0<x3,
∴y1<y2<0,y3<0.
∴下列结论可能成立的是A,
故选:A.
8.解:设运动时间为x秒,四边形APQC的面积为ycm2,
则AP=xcm,BQ=2xcm,
∴BP=(4﹣x)cm,
∴y=S△ABC﹣S△PBQ=BC AB﹣BQ BP,
即y=×8×4﹣×2x(4﹣x)=x2﹣4x+16=(x﹣2)2+12,
∴当x=2时,y有最小值为12,
故选:B.
9.解:令y=4,则4=(x﹣1)2,
解得x=3或﹣1,
∴A(﹣1,4),
平移直线y=﹣x+m知:直线位于l1和l2时,它与新图象有三个不同的公共点.
①当直线位于l1时,此时l1过点A(﹣1,4),
∴4=1+m,即m=3.
②当直线位于l2时,此时l2与函数y=(x﹣1)2 的图象有一个公共点,
∴方程﹣x+m=x2﹣2x+1,
即x2﹣x+1﹣m=0有两个相等实根,
∴△=1﹣4(1﹣m)=0,
即m=.
由①②知若直线y=﹣x+m与新图象只有四个交点,m的取值范围为<m<3;
故选:A.
10.解:①∵抛物线开口向下,
∴a<0,
∵抛物线的对称轴在y轴右侧,
∴b>0
∵抛物线与y轴交于正半轴,
∴c>0,
∴abc<0,所以①正确;
②当x=﹣1时,y<0,
∴a﹣b+c<0,
∵﹣=1,
∴b=﹣2a,
把b=﹣2a代入a﹣b+c<0中得3a+c<0,所以②错误;
③当x=﹣1时,y<0,
∴a﹣b+c<0,
∴a+c<b,
当x=1时,y>0,
∴a+b+c>0,
∴a+c>﹣b,
∴|a+c|<|b|
∴(a+c)2<b2,即(a+c)2﹣b2<0,所以③正确;
④∵抛物线的对称轴为直线x=1,
∴x=1时,函数的最大值为a+b+c,
∴a+b+c≥am2+mb+c,
即a+b≥m(am+b),所以④错误.
故选:B.
11.解:根据题意=±3,
解得c=8或14.
故选:C.
二.填空题(共10小题,满分30分)
12.解:抛物线的对称轴为直线x=﹣k,
因为a=﹣1<0,
所以抛物线开口向下,
所以当x>﹣k时,y的值随x值的增大而减小,
而x>﹣2时,y的值随x值的增大而减小,
所以﹣k≤﹣2,
所以k≥2.
故答案为k≥2.
13.解:∵二次函数y=mx2+2mx+1=m(x+1)2﹣m+1,
∴对称轴为直线x=﹣1,
①m>0,抛物线开口向上,
x=﹣1时,有最小值y=﹣m+1=﹣2,
解得:m=3;
②m<0,抛物线开口向下,
∵对称轴为直线x=﹣1,在﹣2≤x≤2时有最小值﹣2,
∴x=2时,有最小值y=4m+4m+1=﹣2,
解得:m=﹣;
故答案为:3或.
14.解:∵y=x2﹣2x﹣3=(x﹣1)2﹣4,
∴对称轴为x=1,
∵3≤x≤6时,y随x的增大而增大,
∴x=3时,有最小值,y最小值=22﹣4=0;
故答案为:0.
15.解:∵二次函数y=x2+2mx+1,当x>1时,y随x的增大而增大,
∴﹣≤1,
∴m≥﹣1,
故答案为m≥﹣1.
16.解:∵y=x2﹣4x﹣4=(x﹣2)2﹣8,
∴将抛物线y=(x﹣2)2﹣8向右平移2个单位所得直线解析式为:y=(x﹣4)2﹣8,
再向上平移3个单位为:y=(x﹣4)2﹣5,即y=x2﹣8x+11,
故ab=﹣8×11=﹣88.
故答案为:﹣88.
17.解:二次函数y=(x﹣1)2+1的图象先向右平移2个单位,再向上平移3个单位,平移后图象的函数表达式为:y=(x﹣1﹣2)2+1+3,即y=(x﹣3)2+4.
故答案是:y=(x﹣3)2+4.
18.解:将二次函数y=2x2﹣4x﹣1的图象沿着y轴翻折,所得到的图象对应的函数表达式是y=2(﹣x)2﹣4 (﹣x)﹣1,即y=2x2+4x﹣1,
故答案为y=2x2+4x﹣1,
19.解:∵y=﹣x2+mx,
∴抛物线开口向下,抛物线的对称轴为x=﹣=,
∵=,
①当≤﹣1,即m≤﹣2时,当x=﹣1时,函数最大值为3,
∴﹣1﹣m=3,
解得:m=﹣4;
②当≥2,即m≥4时,当x=2时,函数最大值为3,
∴﹣4+2m=3,
解得:m=(舍去).
③当﹣1<<2,即﹣2<m<4时,当x=时,函数最大值为3,
∴﹣+=3,
解得m=2或m=﹣2(舍去),
综上所述,m=﹣4或m=2,
故答案为﹣4或2.
20.解:将y=2x2﹣4x+3化为顶点式,得y=2(x﹣1)2+1,
抛物线y=2x2﹣4x+3绕坐标原点旋转180°所得的抛物线的解析式是y=﹣2(x+1)2﹣1,
化为一般式,得
y=﹣2x2﹣4x﹣3,
故答案为:y=﹣2x2﹣4x﹣3.
21.解:设矩形的一边长是xcm,则邻边的长是(16﹣x)cm.
则矩形的面积S=x(16﹣x),即S=﹣x2+16x,
当x=﹣=﹣=8时,S有最大值是:64.
故答案是:64.
三.解答题(共10小题,满分57分)
22.解:(1)∵y=﹣x2+2tx﹣t+1=﹣(x﹣t)2+t2﹣t+1,
∴顶点坐标为(t,t2﹣t+1);
(2)∵y=﹣x2+2tx﹣t+1=﹣(x﹣t)2+t2﹣t+1,
∴抛物线开口向下,在对称轴x=t的右边y随x的增大而减小,
∴当x≥t时,y随x的增大而减小,
∵当x≥2时,y随x的增大而减小,
∴t≤2;
(3)∵当0≤x≤1时,该函数有最大值4,
∴①若t<0,则当x=0时,y=﹣t+1=4,
解得,t=﹣3;
②若0≤t≤1,则t2﹣t+1=4,
解得,t=(舍);
③若t>1,则当x=1时,y=﹣1+2t﹣t+1=4,
解得,t=4.
综上,t=﹣3或4.
23.解:(1)∵抛物线的解析式为y=﹣x2+2kx+1﹣k=﹣(x﹣k)2+1﹣k+k2,
∴抛物线的顶点坐标为(k,1﹣k+k2);
(2)∵抛物线的解析式为y=﹣(x﹣k)2+1﹣k+k2,
∴当x≥k时,y随x的增大而减小,
∵当x≥1时,y随x的增大而减小,
∴k≤1.
(3)①当k<0时,x=0时,函数值最大,
∴1﹣k=3,解得k=﹣2;
②当0≤k≤1时,则1﹣k+k2=3,
解得k=2或﹣1(舍去),
③当k>1时,x=1时,函数值最大,
∴﹣1+2k+1﹣k=3,解得k=3
综上,当0≤x≤1时,该函数有最大值3,则k=﹣2或k=3.
24.解:(1)抛物线y=﹣2(x﹣2)2的顶点坐标(2,0),开口方向向下,对称轴为直线x=2;
(2)y=﹣2x2的顶点坐标为(0,0),y=﹣2(x﹣2)2的顶点坐标为(2,0),y=﹣2(x﹣2)2+2的顶点坐标为(2,2),
所以,抛物线y=﹣2x2向右平移2个单位得到抛物线y=﹣2(x﹣2)2,
抛物线y=﹣2x2向右平移2个单位,再向上平移2个单位得到抛物线y=﹣2(x﹣2)2+2;
(3)∵抛物线y=﹣2(x﹣2017)2﹣2018的顶点坐标为(2017,﹣2018),
∴应将y=﹣2x2向右平移2017个单位,向下平移2018个单位得到.
25.解:(1)根据题意得m+2≠0且m2+m﹣4=2,
解得m1=2,m2=﹣3,
所以满足条件的m值为2或﹣3;
(2)当m+2>0时,抛物线有最低点,
所以m=2,
抛物线解析式为y=4x2,
所以抛物线的最低点为(0,0),当x≥0时,y随x的增大而增大;
(3)当m=﹣3时,抛物线开口向下,函数有最大值;
抛物线解析式为y=﹣x2,
所以二次函数的最大值是0,这时,当x≥0时,y随x的增大而减小.
26.解:(1)当m=1时,y=﹣x2+4x﹣3=﹣(x﹣2)2+1,
∴顶点坐标为(2,1);
(2)由抛物线y=﹣x2+4x+m﹣4(m为常数)可知:开口向上,函数的对称轴为直线x=2,
∴当3≤x≤3+m时,y随x的增大而减小,
∴当x=m+3时,y有最小值﹣7,
∴﹣(m+3)2+4(m+3)+m﹣4=﹣7,
解得m1=2,m2=﹣3(舍去),
∴m=2;
(3)∵M(3,0),N(0,﹣2),
∴直线MN的解析式为y=x﹣2,
∵抛物线与线段MN有公共点,则方程﹣x2+4x+m﹣4=x﹣2,即x2﹣x﹣m+2=0中△≥0,且m﹣4≤﹣2,
∴(﹣)2﹣4(﹣m+2)≥0,
解得﹣≤m≤2,
故答案为﹣≤m≤2.
27.解:(1)∵直线AB的解析式为:y=kx+2k+4=k(x+2)+4,
∴直线AB总经过一个定点C,点C的坐标为(﹣2,4).
(2)过点P作PD∥y轴交直线AB于点D,如图所示.
当k=﹣时,直线AB的解析式为y=﹣x+3,
联立直线AB与抛物线解析式成方程组,得:
,解得:,,
∴点A的坐标为(﹣3,),点B的坐标为(2,2).
设点P的坐标为(m,m2)(﹣3<m<2),则点D的坐标为(m,﹣m+3),
∴S△ABP=PD (xB﹣xA)=×(﹣m+3﹣m2)×[2﹣(﹣3)]=×(﹣m2﹣m+3)=5,
解得:m1=﹣2,m2=1,
∴点P的坐标为(﹣2,2)或(1,).
28.解:(1)∵y=﹣x2+2x+3=﹣(x﹣1)2+4,
∴顶点M的坐标是(1,4),对称轴是直线x=1,
∵ME⊥y轴,
∴点E的坐标是(0,4),
解方程﹣x2+2x+3=0得x1=﹣1,x2=3,
∴A(﹣1,0),B(3,0),
设直线BE的解析式为y=kx+b,
把B(3,0),E(0,4)代入得,解得,
∴直线BE的解析式为y=﹣x+4,
∵当x=1时,y=﹣x+4=,
∴所以F的坐标是(1,);
(2)由(1)可得EM=1,MF=4﹣=,FN=,BN=3﹣1=2,
S△EFM+S△BNF= 1 + 2 =.
29.解:(1)设经过t秒后,△PBQ的面积等于8cm2.
×(6﹣t)×2t=8,
解得:t1=2,t2=4,
答:经过2或4秒后,△PBQ的面积等于8cm2.
(2)依题意,得S=×PB×BQ=×(6﹣t)×2t=﹣t2+6t=﹣(t﹣3)2+9,
∴在移动过程中,△PBQ的最大面积是9cm2.
30.解:抛物线C2与抛物线C1关于x轴对称,横坐标不变,纵坐标互为相反数,即﹣y=2x2﹣4x+5,
因此所求抛物线C2的解析式是y=﹣2x2+4x﹣5.
31.解:(1)∵抛物线y=ax2+bx+经过点A(﹣1,0),B(4,),
∴解得,
∴抛物线解析式为y=﹣x2+2x+.
(2)设点D坐标为(m,﹣m2+2m+),直线DC⊥x轴,与AB交于点C,
∵直线AB解析式为y=x+,
∴点C坐标(m,m+),
∵S△ABD=S△ACD+S△BCD=(﹣m2+2m+﹣m﹣)×(4+1)=﹣(m2﹣3m﹣4)=﹣(m﹣)2+,
∴当m=时,△ADB面积最大,此时点D坐标(,).
优生辅导测评(附答案)
一.选择题(共11小题,满分33分)
1.二次函数y=ax2+4ax+1﹣a的图象只过三个象限,则a的取值范围为( )
A.<a≤1 B.0<a< C.﹣1<a<0 D.a<﹣1
2.在同一平面直角坐标系中,函数y=mx+m和函数y=﹣mx2+2x+2(m是常数,且m≠0)的图象可能是( )
A.B.C.D.
3.对称轴为直线x=1的抛物线y=ax2+bx+c(a、b、c为常数,且a≠0)如图所示,小明同学得出了以下结论:①abc<0,②b2>4ac,③4a+2b+c>0,④3a+c>0,⑤(a+c)2<b2.其中结论正确的为( )
A.①②④ B.②③⑤ C.②④⑤ D.②③④
4.二次函数y=ax2+bx+c(a≠0)的部分图象如图所示,有以下结论:①a﹣b+c<0;②abc>0;③2a﹣b<0;④3a+c=0;⑤>4a,其中正确的个数为( )
A.1个 B.2个 C.3个 D.4个
5.二次函数y=ax2+bx+c(a≠0)的图象如图所示.下列结论:①abc>0;②2a+b=0;③m为任意实数,则a+b>am2+bm;④a﹣b+c>0;⑤若ax12+bx1=ax22+bx2且x1≠x2,则x1+x2=2.其中正确的有( )
A.①④ B.③④ C.②⑤ D.②③⑤
6.二次函数y=ax2+bx+c(a≠0)的图象如图,给出下列四个结论:
①3a+2b+c<0;
②3a+c<b2﹣4ac;
③方程2ax2+2bx+2c﹣5=0没有实数根;
④m(am+b)+b<a(m≠﹣1).
其中正确结论的个数是( )
A.4个 B.3个 C.2个 D.1个
7.已知点A(x1.y1),B(x2、y2),C(x3、y3)都在二次函数y=ax2(a<0)的图象上.且x1<x2<0<x3,则下列结论可能成立的是( )
A.y1<y2<y3<0 B.0<y1<y2<y3 C.y1<y2<0<y3 D.y3<y2<y1<0
8.如图,在△ABC中,∠B=90°,AB=4cm,BC=8cm.动点P从点A出发,沿边AB向点B以1cm/s的速度移动(不与点B重合),同时动点Q从点B出发,沿边BC向点C以2cm/s的速度移动(不与点C重合).当四边形APQC的面积最小时,经过的时间为( )
A.1s B.2s C.3s D.4s
9.如图,将抛物线y=(x﹣1)2的图象位于直线y=4以上的部分向下翻折,得到新的图象(实线部分),若直线y=﹣x+m与新图象只有四个交点,求m的取值范围.( )
A.<m<3 B.<m<7 C.<m<7 D.<m<3
10.二次函数y=ax2+bx+c的图象如图所示,对称轴是直线x=1.下列结论:①abc<0;②3a+c>0;③(a+c)2﹣b2<0;④a+b≤m(am+b)(m为实数).其中结论正确的个数为( )
A.1个 B.2个 C.3个 D.4个
11.如果抛物线y=x2﹣6x+c﹣2的顶点到x轴的距离是3,那么c的值等于( )
A.8 B.14 C.8或14 D.﹣8或﹣14
二.填空题(共10小题,满分30分)
12.已知二次函数y=﹣(x+k)2+h,当x>﹣2时,y随x的增大而减小,则k的取值范围是 .
13.已知二次函数y=mx2+2mx+1(m≠0)在﹣2≤x≤2时有最小值﹣2,则m= .
14.二次函数y=x2﹣2x﹣3(3≤x≤6)的最小值是 .
15.已知二次函数y=x2+2mx+1,若x>1时,y随x的增大而增大,则m的取值范围是 .
16.将二次函数y=x2﹣4x﹣4的图象先向上平移3个单位长度,再向右平移2个单位长度得到的图象对应的二次函数的解析式为y=x2+ax+b,则ab= .
17.二次函数y=(x﹣1)2+1的图象先向右平移2个单位,再向上平移3个单位,平移后图象的函数表达式为 .
18.将二次函数y=2x2﹣4x﹣1的图象沿着y轴翻折,所得到的图象对应的函数表达式是 .
19.若二次函数y=﹣x2+mx在﹣1≤x≤2时的最大值为3,那么m的值是 .
20.抛物线y=2x2﹣4x+3绕坐标原点旋转180°所得的抛物线的解析式是 .
21.用一根长为32cm的铁丝围成一个矩形,则围成矩形面积的最大值是 cm2.
三.解答题(共10小题,满分57分)
22.已知二次函数y=﹣x2+2tx﹣t+1(是常数).
(1)求此函数的顶点坐标.(用含t的代数式表示)
(2)当x≥2时,y随x的增大而减小,求t的取值范围.
(3)当0≤x≤1时,该函数有最大值4,求t的值.
23.已知二次函数y=﹣x2+2kx+1﹣k(k是常数)
(1)求此函数的顶点坐标.
(2)当x≥1时,y随x的增大而减小,求k的取值范围.
(3)当0≤x≤1时,该函数有最大值3,求k的值.
24.已知二次函数y=﹣2x2,y=﹣2(x﹣2)2,y=﹣2(x﹣2)2+2,请回答下列问题:
(1)写出抛物线y=﹣2(x﹣2)2的顶点坐标,开口方向和对称轴;
(2)分别通过怎样的平移,可以由抛物线y=﹣2x2得到抛物线y=﹣2(x﹣2)2和y=﹣2(x﹣2)2+2?
(3)如果要得到抛物线y=﹣2(x﹣2017)2﹣2018,应将y=﹣2x2怎样平移?
25.函数y=(m+2)是关于x的二次函数,求:
(1)满足条件的m值;
(2)m为何值时,抛物线有最低点?求出这个最低点.这时,当x为何值时,y随x的增大而增大?
(3)m为何值时,函数有最大值?最大值是多少?这时,当x为何值时,y随x的增大而减小.
26.如图,平面直角坐标系中,抛物线y=﹣x2+4x+m﹣4(m为常数)与y轴的交点为C,M(3,0)与N(0,﹣2)分别是x轴、y轴上的点
(1)当m=1时,求抛物线顶点坐标.
(2)若3≤x≤3+m时,函数y=﹣x2+4x+m﹣4有最小值﹣7,求m的值.
(3)若抛物线与线段MN有公共点,直接写出m的取值范围是 .
27.如图,已知直线AB:y=kx+2k+4与抛物线y=x2交于A、B两点.
(1)直线AB总经过一个定点C,请直接写出点C坐标;
(2)当k=﹣时,在直线AB下方的抛物线上求点P,使△ABP的面积等于5.
28.如图,抛物线y=﹣x2+2x+3与x轴交于A,B两点,它的对称轴与x轴交于点N,过顶点M作ME⊥y轴于点E,连接BE交MN于点F.
(1)求F的坐标.
(2)求△EMF与△BNF的面积之和.
29.如图,在△ABC中,∠B=90°,AB=6cm,BC=8cm,点P从A点开始沿AB边向点B以1cm/秒的速度移动,同时点Q从B点开始沿BC边向点C以2cm/秒的速度移动,且当其中一点到达终点时,另一个点随之停止移动.
(1)P,Q两点出发几秒后,可使△PBQ的面积为8cm2.
(2)设P,Q两点同时出发移动的时间为t秒,△PBQ的面积为Scm2,请写出S与t的函数关系式,并求出△PBQ面积的最大值.
30.已知抛物线C1的解析式是y=2x2﹣4x+5,抛物线C2与抛物线C1关于x轴对称,求抛物线C2的解析式.
31.如图.抛物线y=ax2+bx+与直线AB交于点A(﹣1,0),B(4,),点D是抛物线上位于直线AB上方的一点(不与点A,B重合),连接AD,BD.
(1)求抛物线的解析;
(2)设△ADB的面为S,求出当S取最大值时的点D的坐标.
参考答案
一.选择题(共11小题,满分33分)
1.解:∵抛物线的对称轴为直线x=﹣=﹣2,抛物线图象只过三个象限,
∴当a>0,抛物线经过第一、二、三象限,当a<0,抛物线经过第二、三、四象限
∴当a>0时,,解得<a≤1;
当a<0时,,无解,
所以a的范围为<a≤1;
故选:A.
2.解:A、由函数y=mx+m的图象可知m<0,即函数y=﹣mx2+2x+2开口方向朝上,与图象不符,故A选项错误;
B、由函数y=mx+m的图象可知m<0,对称轴为x=﹣=﹣=<0,则对称轴应在y轴左侧,与图象不符,故B选项错误;
C、由函数y=mx+m的图象可知m>0,即函数y=﹣mx2+2x+2开口方向朝下,与图象不符,故C选项错误;
D、由函数y=mx+m的图象可知m<0,即函数y=﹣mx2+2x+2开口方向朝上,对称轴为x=﹣=﹣=<0,则对称轴应在y轴左侧,与图象相符,故D选项正确;
故选:D.
3.解:①由图象可知:a>0,c<0,
∵﹣=1,
∴b=﹣2a<0,
∴abc>0,故①错误;
②∵抛物线与x轴有两个交点,
∴b2﹣4ac>0,
∴b2>4ac,故②正确;
③当x=2时,y=4a+2b+c<0,故③错误;
④当x=﹣1时,y=a﹣b+c=a﹣(﹣2a)+c>0,
∴3a+c>0,故④正确;
⑤当x=﹣1时,y>0,即:a﹣b+c>0.
当x=1时,y<0,即:a+b+c<0
两式相乘得(a+c)2﹣b2<0,
∴(a+c)2<b2.故⑤正确.
故选:C.
4.解:由图象可知,当x=﹣1时,y=a﹣b+c>0,
∴①不合题意,
∵抛物线的开口向下,
∴a<0,
∵抛物线与y轴的交点在x轴的上方,
∴c>0,
∵抛物线的对称轴为x=﹣1,
∴,即b=2a,
∴b<0,
∴abc>0,
∴②符合题意,
∵抛物线的对称轴为x=﹣1,
∴,即b=2a,
∴2a﹣b=0,
∴③不合题意,
由图象可知,抛物线与x轴的另一个交点为(1,0),
∴当x=1时,y=a+b+c=a+2a+c=3a+c=0,
∴④符合题意,
∵,
∴,
∴⑤符合题意,
∴符合题意的有三个,
故选:C.
5.解:①抛物线开口方向向下,则a<0.
抛物线对称轴位于y轴右侧,则a、b异号,即ab<0.
抛物线与y轴交于正半轴,则c>0.
所以abc<0.
故①错误.
②∵抛物线对称轴为直线x==1,
∴b=﹣2a,即2a+b=0,
故②正确;
③∵抛物线对称轴为直线x=1,
∴函数的最大值为:a+b+c,
∴a+b+c≥am2+bm+c,即a+b≥am2+bm,
故③错误;
④∵抛物线与x轴的一个交点在(3,0)的左侧,而对称轴为直线x=1,
∴抛物线与x轴的另一个交点在(﹣1,0)的右侧
∴当x=﹣1时,y<0,
∴a﹣b+c<0,
故④错误;
⑤∵ax12+bx1=ax22+bx2,
∴ax12+bx1﹣ax22﹣bx2=0,
∴a(x1+x2)(x1﹣x2)+b(x1﹣x2)=0,
∴(x1﹣x2)[a(x1+x2)+b]=0,
而x1≠x2,
∴a(x1+x2)+b=0,即x1+x2=,
∵b=﹣2a,
∴x1+x2=2,
故⑤正确.
综上所述,正确的有②⑤.
故选:C.
6.解:由图象可知,当x=1时,y<0,即a+b+c<0,
∵对称轴x=﹣=﹣1,a<0,
∴b=2a<0,
∴a+2a+c<0,即3a+c<0,
∴3a+2b+c<0,故①正确;
∵抛物线与x轴有两个交点,
∴b2﹣4ac>0,
∴3a+c<0<b2﹣4ac,故②正确;
∵2ax2+2bx+2c﹣5=0,
∴ax2+bx+c=,
结合图象可知,不能确定抛物线y=ax2+bx+c与直线y=的交点情况,
故③不正确;
∵当x=m(m≠﹣1)时,y=am2+bm+c,且当x=﹣1时,函数y取得最大值,
∴a﹣b+c>am2+bm+c,
∴m(am+b)+b<a,故④正确;
综上,正确结论有①②④共3个,
故选:B.
7.解:∵二次函数y=ax2的对称轴为y轴,开口向下,且关于y轴对称,
∴x<0时,y随x的增大而增大,
∵x1<x2<0<x3,
∴y1<y2<0,y3<0.
∴下列结论可能成立的是A,
故选:A.
8.解:设运动时间为x秒,四边形APQC的面积为ycm2,
则AP=xcm,BQ=2xcm,
∴BP=(4﹣x)cm,
∴y=S△ABC﹣S△PBQ=BC AB﹣BQ BP,
即y=×8×4﹣×2x(4﹣x)=x2﹣4x+16=(x﹣2)2+12,
∴当x=2时,y有最小值为12,
故选:B.
9.解:令y=4,则4=(x﹣1)2,
解得x=3或﹣1,
∴A(﹣1,4),
平移直线y=﹣x+m知:直线位于l1和l2时,它与新图象有三个不同的公共点.
①当直线位于l1时,此时l1过点A(﹣1,4),
∴4=1+m,即m=3.
②当直线位于l2时,此时l2与函数y=(x﹣1)2 的图象有一个公共点,
∴方程﹣x+m=x2﹣2x+1,
即x2﹣x+1﹣m=0有两个相等实根,
∴△=1﹣4(1﹣m)=0,
即m=.
由①②知若直线y=﹣x+m与新图象只有四个交点,m的取值范围为<m<3;
故选:A.
10.解:①∵抛物线开口向下,
∴a<0,
∵抛物线的对称轴在y轴右侧,
∴b>0
∵抛物线与y轴交于正半轴,
∴c>0,
∴abc<0,所以①正确;
②当x=﹣1时,y<0,
∴a﹣b+c<0,
∵﹣=1,
∴b=﹣2a,
把b=﹣2a代入a﹣b+c<0中得3a+c<0,所以②错误;
③当x=﹣1时,y<0,
∴a﹣b+c<0,
∴a+c<b,
当x=1时,y>0,
∴a+b+c>0,
∴a+c>﹣b,
∴|a+c|<|b|
∴(a+c)2<b2,即(a+c)2﹣b2<0,所以③正确;
④∵抛物线的对称轴为直线x=1,
∴x=1时,函数的最大值为a+b+c,
∴a+b+c≥am2+mb+c,
即a+b≥m(am+b),所以④错误.
故选:B.
11.解:根据题意=±3,
解得c=8或14.
故选:C.
二.填空题(共10小题,满分30分)
12.解:抛物线的对称轴为直线x=﹣k,
因为a=﹣1<0,
所以抛物线开口向下,
所以当x>﹣k时,y的值随x值的增大而减小,
而x>﹣2时,y的值随x值的增大而减小,
所以﹣k≤﹣2,
所以k≥2.
故答案为k≥2.
13.解:∵二次函数y=mx2+2mx+1=m(x+1)2﹣m+1,
∴对称轴为直线x=﹣1,
①m>0,抛物线开口向上,
x=﹣1时,有最小值y=﹣m+1=﹣2,
解得:m=3;
②m<0,抛物线开口向下,
∵对称轴为直线x=﹣1,在﹣2≤x≤2时有最小值﹣2,
∴x=2时,有最小值y=4m+4m+1=﹣2,
解得:m=﹣;
故答案为:3或.
14.解:∵y=x2﹣2x﹣3=(x﹣1)2﹣4,
∴对称轴为x=1,
∵3≤x≤6时,y随x的增大而增大,
∴x=3时,有最小值,y最小值=22﹣4=0;
故答案为:0.
15.解:∵二次函数y=x2+2mx+1,当x>1时,y随x的增大而增大,
∴﹣≤1,
∴m≥﹣1,
故答案为m≥﹣1.
16.解:∵y=x2﹣4x﹣4=(x﹣2)2﹣8,
∴将抛物线y=(x﹣2)2﹣8向右平移2个单位所得直线解析式为:y=(x﹣4)2﹣8,
再向上平移3个单位为:y=(x﹣4)2﹣5,即y=x2﹣8x+11,
故ab=﹣8×11=﹣88.
故答案为:﹣88.
17.解:二次函数y=(x﹣1)2+1的图象先向右平移2个单位,再向上平移3个单位,平移后图象的函数表达式为:y=(x﹣1﹣2)2+1+3,即y=(x﹣3)2+4.
故答案是:y=(x﹣3)2+4.
18.解:将二次函数y=2x2﹣4x﹣1的图象沿着y轴翻折,所得到的图象对应的函数表达式是y=2(﹣x)2﹣4 (﹣x)﹣1,即y=2x2+4x﹣1,
故答案为y=2x2+4x﹣1,
19.解:∵y=﹣x2+mx,
∴抛物线开口向下,抛物线的对称轴为x=﹣=,
∵=,
①当≤﹣1,即m≤﹣2时,当x=﹣1时,函数最大值为3,
∴﹣1﹣m=3,
解得:m=﹣4;
②当≥2,即m≥4时,当x=2时,函数最大值为3,
∴﹣4+2m=3,
解得:m=(舍去).
③当﹣1<<2,即﹣2<m<4时,当x=时,函数最大值为3,
∴﹣+=3,
解得m=2或m=﹣2(舍去),
综上所述,m=﹣4或m=2,
故答案为﹣4或2.
20.解:将y=2x2﹣4x+3化为顶点式,得y=2(x﹣1)2+1,
抛物线y=2x2﹣4x+3绕坐标原点旋转180°所得的抛物线的解析式是y=﹣2(x+1)2﹣1,
化为一般式,得
y=﹣2x2﹣4x﹣3,
故答案为:y=﹣2x2﹣4x﹣3.
21.解:设矩形的一边长是xcm,则邻边的长是(16﹣x)cm.
则矩形的面积S=x(16﹣x),即S=﹣x2+16x,
当x=﹣=﹣=8时,S有最大值是:64.
故答案是:64.
三.解答题(共10小题,满分57分)
22.解:(1)∵y=﹣x2+2tx﹣t+1=﹣(x﹣t)2+t2﹣t+1,
∴顶点坐标为(t,t2﹣t+1);
(2)∵y=﹣x2+2tx﹣t+1=﹣(x﹣t)2+t2﹣t+1,
∴抛物线开口向下,在对称轴x=t的右边y随x的增大而减小,
∴当x≥t时,y随x的增大而减小,
∵当x≥2时,y随x的增大而减小,
∴t≤2;
(3)∵当0≤x≤1时,该函数有最大值4,
∴①若t<0,则当x=0时,y=﹣t+1=4,
解得,t=﹣3;
②若0≤t≤1,则t2﹣t+1=4,
解得,t=(舍);
③若t>1,则当x=1时,y=﹣1+2t﹣t+1=4,
解得,t=4.
综上,t=﹣3或4.
23.解:(1)∵抛物线的解析式为y=﹣x2+2kx+1﹣k=﹣(x﹣k)2+1﹣k+k2,
∴抛物线的顶点坐标为(k,1﹣k+k2);
(2)∵抛物线的解析式为y=﹣(x﹣k)2+1﹣k+k2,
∴当x≥k时,y随x的增大而减小,
∵当x≥1时,y随x的增大而减小,
∴k≤1.
(3)①当k<0时,x=0时,函数值最大,
∴1﹣k=3,解得k=﹣2;
②当0≤k≤1时,则1﹣k+k2=3,
解得k=2或﹣1(舍去),
③当k>1时,x=1时,函数值最大,
∴﹣1+2k+1﹣k=3,解得k=3
综上,当0≤x≤1时,该函数有最大值3,则k=﹣2或k=3.
24.解:(1)抛物线y=﹣2(x﹣2)2的顶点坐标(2,0),开口方向向下,对称轴为直线x=2;
(2)y=﹣2x2的顶点坐标为(0,0),y=﹣2(x﹣2)2的顶点坐标为(2,0),y=﹣2(x﹣2)2+2的顶点坐标为(2,2),
所以,抛物线y=﹣2x2向右平移2个单位得到抛物线y=﹣2(x﹣2)2,
抛物线y=﹣2x2向右平移2个单位,再向上平移2个单位得到抛物线y=﹣2(x﹣2)2+2;
(3)∵抛物线y=﹣2(x﹣2017)2﹣2018的顶点坐标为(2017,﹣2018),
∴应将y=﹣2x2向右平移2017个单位,向下平移2018个单位得到.
25.解:(1)根据题意得m+2≠0且m2+m﹣4=2,
解得m1=2,m2=﹣3,
所以满足条件的m值为2或﹣3;
(2)当m+2>0时,抛物线有最低点,
所以m=2,
抛物线解析式为y=4x2,
所以抛物线的最低点为(0,0),当x≥0时,y随x的增大而增大;
(3)当m=﹣3时,抛物线开口向下,函数有最大值;
抛物线解析式为y=﹣x2,
所以二次函数的最大值是0,这时,当x≥0时,y随x的增大而减小.
26.解:(1)当m=1时,y=﹣x2+4x﹣3=﹣(x﹣2)2+1,
∴顶点坐标为(2,1);
(2)由抛物线y=﹣x2+4x+m﹣4(m为常数)可知:开口向上,函数的对称轴为直线x=2,
∴当3≤x≤3+m时,y随x的增大而减小,
∴当x=m+3时,y有最小值﹣7,
∴﹣(m+3)2+4(m+3)+m﹣4=﹣7,
解得m1=2,m2=﹣3(舍去),
∴m=2;
(3)∵M(3,0),N(0,﹣2),
∴直线MN的解析式为y=x﹣2,
∵抛物线与线段MN有公共点,则方程﹣x2+4x+m﹣4=x﹣2,即x2﹣x﹣m+2=0中△≥0,且m﹣4≤﹣2,
∴(﹣)2﹣4(﹣m+2)≥0,
解得﹣≤m≤2,
故答案为﹣≤m≤2.
27.解:(1)∵直线AB的解析式为:y=kx+2k+4=k(x+2)+4,
∴直线AB总经过一个定点C,点C的坐标为(﹣2,4).
(2)过点P作PD∥y轴交直线AB于点D,如图所示.
当k=﹣时,直线AB的解析式为y=﹣x+3,
联立直线AB与抛物线解析式成方程组,得:
,解得:,,
∴点A的坐标为(﹣3,),点B的坐标为(2,2).
设点P的坐标为(m,m2)(﹣3<m<2),则点D的坐标为(m,﹣m+3),
∴S△ABP=PD (xB﹣xA)=×(﹣m+3﹣m2)×[2﹣(﹣3)]=×(﹣m2﹣m+3)=5,
解得:m1=﹣2,m2=1,
∴点P的坐标为(﹣2,2)或(1,).
28.解:(1)∵y=﹣x2+2x+3=﹣(x﹣1)2+4,
∴顶点M的坐标是(1,4),对称轴是直线x=1,
∵ME⊥y轴,
∴点E的坐标是(0,4),
解方程﹣x2+2x+3=0得x1=﹣1,x2=3,
∴A(﹣1,0),B(3,0),
设直线BE的解析式为y=kx+b,
把B(3,0),E(0,4)代入得,解得,
∴直线BE的解析式为y=﹣x+4,
∵当x=1时,y=﹣x+4=,
∴所以F的坐标是(1,);
(2)由(1)可得EM=1,MF=4﹣=,FN=,BN=3﹣1=2,
S△EFM+S△BNF= 1 + 2 =.
29.解:(1)设经过t秒后,△PBQ的面积等于8cm2.
×(6﹣t)×2t=8,
解得:t1=2,t2=4,
答:经过2或4秒后,△PBQ的面积等于8cm2.
(2)依题意,得S=×PB×BQ=×(6﹣t)×2t=﹣t2+6t=﹣(t﹣3)2+9,
∴在移动过程中,△PBQ的最大面积是9cm2.
30.解:抛物线C2与抛物线C1关于x轴对称,横坐标不变,纵坐标互为相反数,即﹣y=2x2﹣4x+5,
因此所求抛物线C2的解析式是y=﹣2x2+4x﹣5.
31.解:(1)∵抛物线y=ax2+bx+经过点A(﹣1,0),B(4,),
∴解得,
∴抛物线解析式为y=﹣x2+2x+.
(2)设点D坐标为(m,﹣m2+2m+),直线DC⊥x轴,与AB交于点C,
∵直线AB解析式为y=x+,
∴点C坐标(m,m+),
∵S△ABD=S△ACD+S△BCD=(﹣m2+2m+﹣m﹣)×(4+1)=﹣(m2﹣3m﹣4)=﹣(m﹣)2+,
∴当m=时,△ADB面积最大,此时点D坐标(,).
