苏科版八年级数学上册 4.3 实数 教案
文档属性
| 名称 | 苏科版八年级数学上册 4.3 实数 教案 | 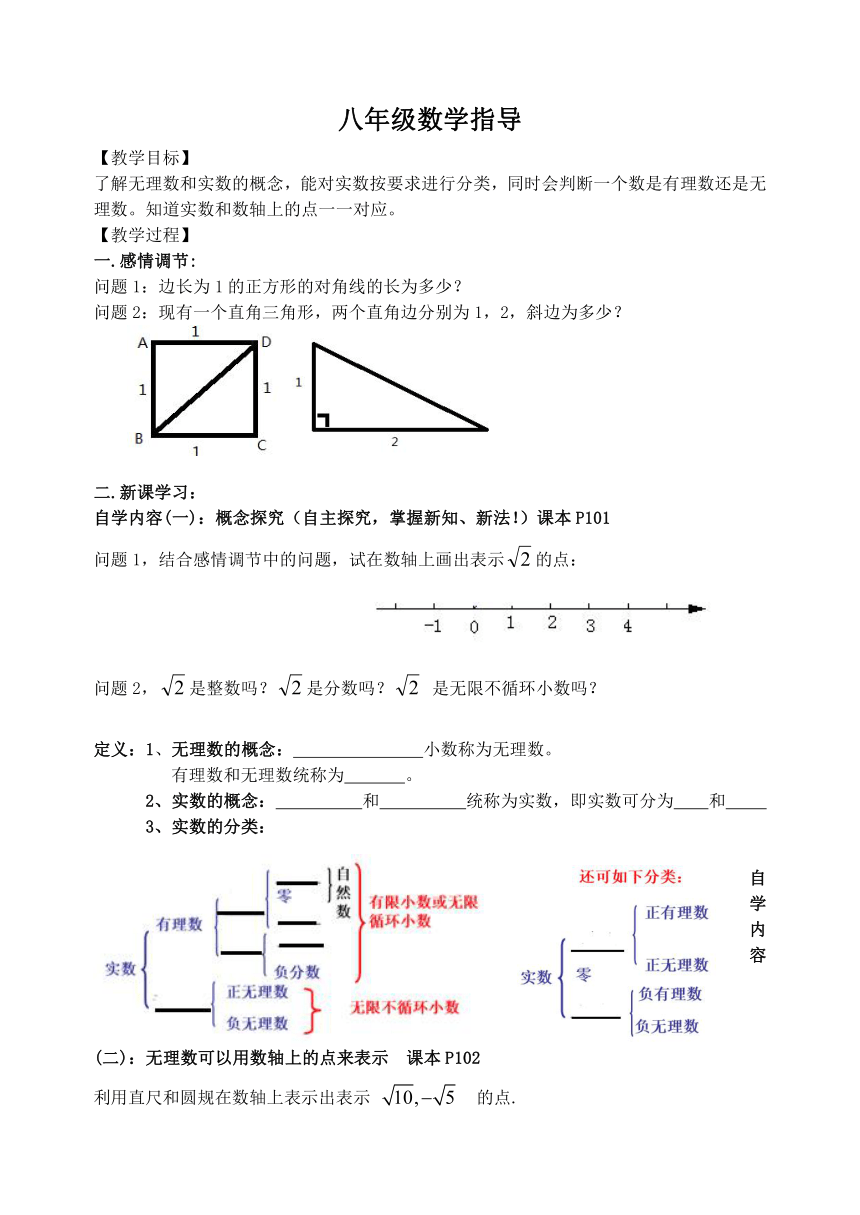 | |
| 格式 | docx | ||
| 文件大小 | 116.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 苏科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-10-20 08:22:43 | ||
图片预览


文档简介
八年级数学指导
【教学目标】
了解无理数和实数的概念,能对实数按要求进行分类,同时会判断一个数是有理数还是无理数。知道实数和数轴上的点一一对应。
【教学过程】
感情调节:
问题1:边长为1的正方形的对角线的长为多少?
问题2:现有一个直角三角形,两个直角边分别为1,2,斜边为多少?
二.新课学习:
自学内容(一):概念探究(自主探究,掌握新知、新法!)课本P101
问题1,结合感情调节中的问题,试在数轴上画出表示的点:
问题2,是整数吗?是分数吗? 是无限不循环小数吗?
定义:1、无理数的概念: 小数称为无理数。
有理数和无理数统称为 。
2、实数的概念: 和 统称为实数,即实数可分为 和
3、实数的分类:
自学内容(二):无理数可以用数轴上的点来表示 课本P102
利用直尺和圆规在数轴上表示出表示 的点.
结论:每一个实数都可以用数轴上的一个点来表示,反之,数轴上的每一个点都
表示一个 数 。 与数轴上的点 对应。
思考:的整数部分是: ,小数部分: ,那呢?
三.自主小结:(适时小结,构建、完善知识体系!)
当堂检测:(当堂检测,熟练掌握新知、新法!)
1.判断:
无理数都是无限小数 ( ) (2)无限小数都是无理数 ( )
(3)是分数( ) (4)是无理数 ( )
2. 在,﹣,,3.14,,,,,5π,0,,1.2626626662…中,属于无理数的有 个.
3.的整数部分是 小数部分是
4. 利用直尺和圆规在数轴上表示出表示
五.适度作业 班级: 姓名:
(一)核心价值题:
1.实数-1.732,,,0.121121112…,中,无理数的个数有 ( ).
A. 2个 B. 3个 C. 4个 D. 5个
2. 下列说法: (1)无限小数是无理数 (2)无理数都是无限小数
(3)有理数都是实数 (4)实数可分为正实数和负实数
(5)带根号的数都是无理数 (6)实数与数轴上的点一一对应 .
正确的个数是 ( )
A.5 B.4 C.3 D.2
3. 大家知道是一个无理数,那么—1在哪两个整数之间 ( )
A.1与2 B.2与3 C.3与4 D.4与5
4. 对于“”,下面说法不正确的是( )
A.它是一个无理数
B.它是数轴上离原点个单位长度的点表示的数
C.若a<<a+1,则整数a为2
D.它表示面积为7的正方形的边长
5. 已知x2=3,那么在数轴上与实数x对应的点可能是( )
A.P1 B.P4 C.P2或P3 D.P1或P4
6. 若无理数a满足:-1请你在横线上写一个负无理数_______.
7. 在数轴上离原点距离是的点表示的数是_______
8. 如图所示:数轴上点A所表示的数为a,则a的值是 .
9. 设2+的整数部分和小数部分分别是x、y,试求x、y的值与x-1的算术平方根.
10. 利用直尺和圆规在数轴上表示出表示 的点.
11.如图,正方形网格中的每个小正方形的边长都是1,每个小格的顶点叫做格点.
(1) 在图(1)中以格点为顶点画一个面积为10的正方形;
(2) 在图(2)中以格点为顶点画一个三角形,使三角形三边长分别为2,,;
(3) 如图(3),点A,B,C是小正方形的顶点,求∠ABC的度数.
(二)知识与演练技能:
12.如图,周长为a的圆上有且仅有一点A在数轴上,点A所表示的数为1,若该圆沿着数轴向右滚动两周后点A对应的点为B,此时,A、B两点之间恰好有三个表示正整数的点(不包括点A、B),则该圆的周长a的取值范围为 .
13.如图,数轴上表示1,的对应点分别为A、B,且AB=AC,设点C所表示的数为x,
求x的值.
(三)知者加速:
14. 观察思考下列计算过程:因为112=121,所以11;同样,因为1112=12321,所以=111,则=_______,可猜想_______.
【教学目标】
了解无理数和实数的概念,能对实数按要求进行分类,同时会判断一个数是有理数还是无理数。知道实数和数轴上的点一一对应。
【教学过程】
感情调节:
问题1:边长为1的正方形的对角线的长为多少?
问题2:现有一个直角三角形,两个直角边分别为1,2,斜边为多少?
二.新课学习:
自学内容(一):概念探究(自主探究,掌握新知、新法!)课本P101
问题1,结合感情调节中的问题,试在数轴上画出表示的点:
问题2,是整数吗?是分数吗? 是无限不循环小数吗?
定义:1、无理数的概念: 小数称为无理数。
有理数和无理数统称为 。
2、实数的概念: 和 统称为实数,即实数可分为 和
3、实数的分类:
自学内容(二):无理数可以用数轴上的点来表示 课本P102
利用直尺和圆规在数轴上表示出表示 的点.
结论:每一个实数都可以用数轴上的一个点来表示,反之,数轴上的每一个点都
表示一个 数 。 与数轴上的点 对应。
思考:的整数部分是: ,小数部分: ,那呢?
三.自主小结:(适时小结,构建、完善知识体系!)
当堂检测:(当堂检测,熟练掌握新知、新法!)
1.判断:
无理数都是无限小数 ( ) (2)无限小数都是无理数 ( )
(3)是分数( ) (4)是无理数 ( )
2. 在,﹣,,3.14,,,,,5π,0,,1.2626626662…中,属于无理数的有 个.
3.的整数部分是 小数部分是
4. 利用直尺和圆规在数轴上表示出表示
五.适度作业 班级: 姓名:
(一)核心价值题:
1.实数-1.732,,,0.121121112…,中,无理数的个数有 ( ).
A. 2个 B. 3个 C. 4个 D. 5个
2. 下列说法: (1)无限小数是无理数 (2)无理数都是无限小数
(3)有理数都是实数 (4)实数可分为正实数和负实数
(5)带根号的数都是无理数 (6)实数与数轴上的点一一对应 .
正确的个数是 ( )
A.5 B.4 C.3 D.2
3. 大家知道是一个无理数,那么—1在哪两个整数之间 ( )
A.1与2 B.2与3 C.3与4 D.4与5
4. 对于“”,下面说法不正确的是( )
A.它是一个无理数
B.它是数轴上离原点个单位长度的点表示的数
C.若a<<a+1,则整数a为2
D.它表示面积为7的正方形的边长
5. 已知x2=3,那么在数轴上与实数x对应的点可能是( )
A.P1 B.P4 C.P2或P3 D.P1或P4
6. 若无理数a满足:-1
7. 在数轴上离原点距离是的点表示的数是_______
8. 如图所示:数轴上点A所表示的数为a,则a的值是 .
9. 设2+的整数部分和小数部分分别是x、y,试求x、y的值与x-1的算术平方根.
10. 利用直尺和圆规在数轴上表示出表示 的点.
11.如图,正方形网格中的每个小正方形的边长都是1,每个小格的顶点叫做格点.
(1) 在图(1)中以格点为顶点画一个面积为10的正方形;
(2) 在图(2)中以格点为顶点画一个三角形,使三角形三边长分别为2,,;
(3) 如图(3),点A,B,C是小正方形的顶点,求∠ABC的度数.
(二)知识与演练技能:
12.如图,周长为a的圆上有且仅有一点A在数轴上,点A所表示的数为1,若该圆沿着数轴向右滚动两周后点A对应的点为B,此时,A、B两点之间恰好有三个表示正整数的点(不包括点A、B),则该圆的周长a的取值范围为 .
13.如图,数轴上表示1,的对应点分别为A、B,且AB=AC,设点C所表示的数为x,
求x的值.
(三)知者加速:
14. 观察思考下列计算过程:因为112=121,所以11;同样,因为1112=12321,所以=111,则=_______,可猜想_______.
同课章节目录
- 第一章 全等三角形
- 1.1 全等图形
- 1.2 全等三角形
- 1.3 探索三角形全等的条件
- 数学活动 关于三角形全等的条件
- 第二章 轴对称图形
- 2.1 轴对称与轴对称图形
- 2.2 轴对称的性质
- 2.3 设计轴对称图案
- 2.4 线段、角的轴对称性
- 2.5 等腰三角形的轴对称性
- 数学活动 折纸与证明
- 第三章 勾股定理
- 3.1 勾股定理
- 3.2 勾股定理的逆定理
- 3.3 勾股定理的简单应用
- 数学活动 探寻“勾股数”
- 第四章 实数
- 4.1 平方根
- 4.2 立方根
- 4.3 实数
- 4.4 近似数
- 数学活动 有关“实数”的课题探究
- 第五章 平面直角坐标系
- 5.1 物体位置的确定
- 5.2 平面直角坐标系
- 数学活动 确定藏宝地
- 第六章 一次函数
- 6.1 函数
- 6.2 一次函数
- 6.3 一次函数的图像
- 6.4 用一次函数解决问题
- 6.5 一次函数与二元一次方程
- 6.6 一次函数、一元一次方程和一元一次不等式
- 数学活动 温度计上的一次函数
