苏科版八年级数学上册 第一章 小结与思考(9)(课件)(共19张PPT)
文档属性
| 名称 | 苏科版八年级数学上册 第一章 小结与思考(9)(课件)(共19张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 1.0MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 苏科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-10-20 08:34:26 | ||
图片预览





文档简介
(共19张PPT)
小结与思考
亚历山大城有一位精通物理和数学的学者海伦,一天一位罗马将军专程去拜访他,向他请教一个百思不得其解的问题,军官每天从军营出发先到河边饮马,然后再去河的同侧帐篷休息,应该怎么走最省时?海伦利用光学性质很快就得到了解答,我们知道光在同一种介质里面是沿直线传播的,也就是说是沿最短路径行进的,但是当光从一点射出后不是直线射向另一点,而是经过平面镜反射到另一点的时候,光依旧会沿最短的路径进行.你说大自然多么奇妙,这个世界冥冥之中是按数学最优美的次序书写的,让人惊叹!从此“将军饮马”问题广为流传.
问题起源
《古从军行》
唐.李欣
白日登山望烽火,黄昏饮马傍交河。
问题起源
江苏科学技术出版社
线段最值问题
—将军饮马
数学是人类思考中最高的成就 ——米斯拉
学习目标
探究并掌握线段最值问题中将军饮马之各种基本图形.
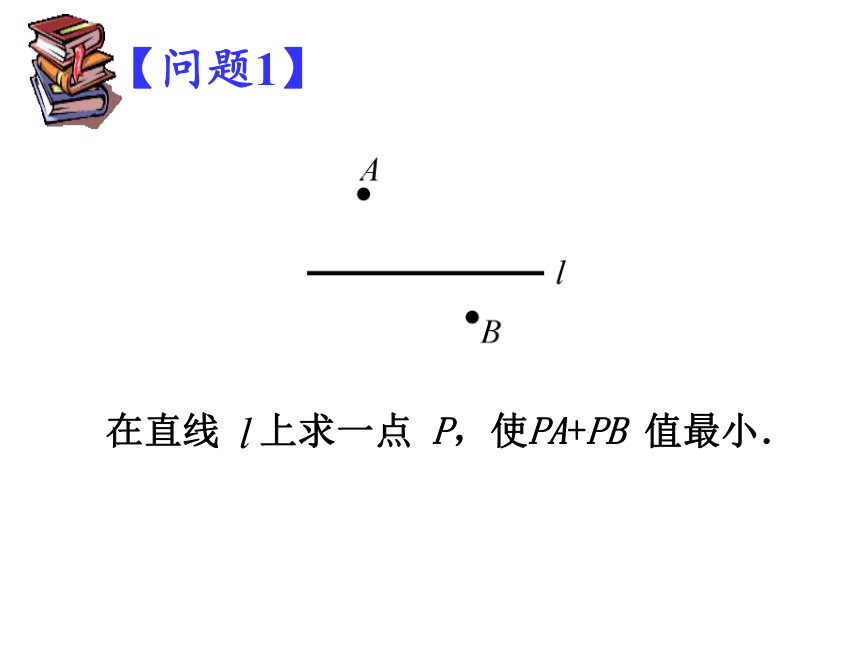
【问题1】
在直线 上求一点 P,使PA+PB 值最小.
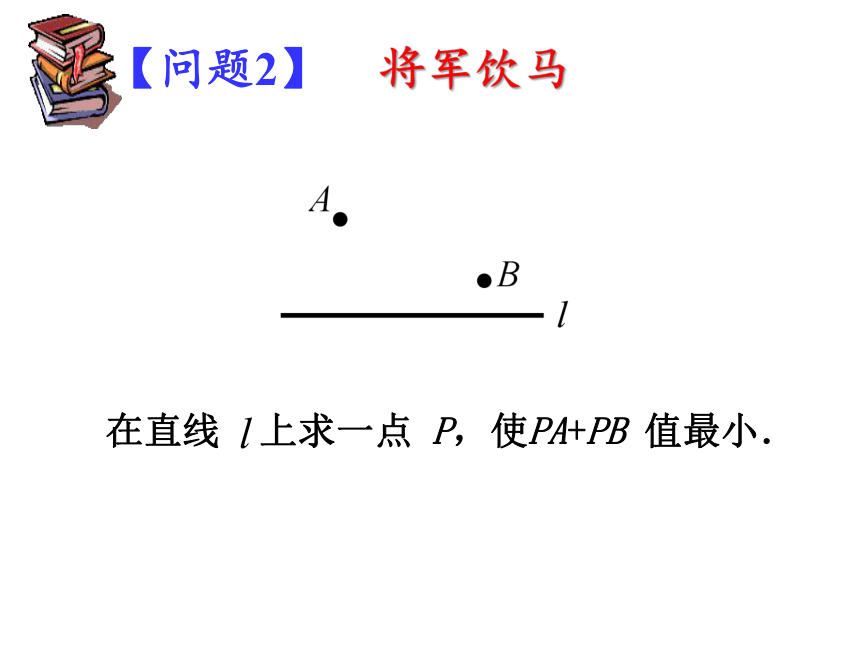
【问题2】
在直线 上求一点 P,使PA+PB 值最小.
将军饮马
【问题3】
在射线 上分别求点M、N,使△PMN 周长最小.
【问题4】
在射线 上分别求点M、N,使四边形PQMN
周长最小.
【问题5】
直线 m∥n ,在 m 、n上分别求点 M、N,
使MN⊥m ,且AM+MN+BN 的值最小.
造桥选址
【问题6】
在直线 上求两点M、N(M 在左),使 MN =a,
并使AM+MN+NB 的值最小.
【问题7】
A为 上一定点,B 为 上一定点,在 上求
点M,在 上求点 N ,使AM+MN+NB 的值最小.
【问题8】
在 上求点A,在 上求点 B,使 PA+AB 值最小.
【问题9】
△ABC 中每一内角都小于 120°,在△ABC 内求
一点P,使 PA+PB+PC 值最小.
费马点
【问题9】
费马点
解答:所求点为“费马点”,
即满足∠APB=∠BPC=∠ APC=120°.
以AB、AC为边向外作等边△ABD、△ACE,
连CD、BE 相交于P,点 P即为所求.
归纳小结
你有哪些收获快和伙伴们分享下吧
必做题:1.等腰△ABC中,CA=CB,M、N分别是两腰中点,在AB上找一点P,使得PM+PN最小。
2.直角坐标系中有正方形OABC,在OB上找一点P,使DP+AP最小。
选做题:
1.矩形ABCD中,AB=20厘米,BC=10厘米,若在AC、AB上各取一点M、N,使MB+MN值最小,求这个最小值。
2.已知定点A(1,2),B(3,4),在x轴找点P,使点P到A、B两点距离之和最短,求P点坐标。
课堂作业
敬请指导
谢 谢
小结与思考
亚历山大城有一位精通物理和数学的学者海伦,一天一位罗马将军专程去拜访他,向他请教一个百思不得其解的问题,军官每天从军营出发先到河边饮马,然后再去河的同侧帐篷休息,应该怎么走最省时?海伦利用光学性质很快就得到了解答,我们知道光在同一种介质里面是沿直线传播的,也就是说是沿最短路径行进的,但是当光从一点射出后不是直线射向另一点,而是经过平面镜反射到另一点的时候,光依旧会沿最短的路径进行.你说大自然多么奇妙,这个世界冥冥之中是按数学最优美的次序书写的,让人惊叹!从此“将军饮马”问题广为流传.
问题起源
《古从军行》
唐.李欣
白日登山望烽火,黄昏饮马傍交河。
问题起源
江苏科学技术出版社
线段最值问题
—将军饮马
数学是人类思考中最高的成就 ——米斯拉
学习目标
探究并掌握线段最值问题中将军饮马之各种基本图形.
【问题1】
在直线 上求一点 P,使PA+PB 值最小.
【问题2】
在直线 上求一点 P,使PA+PB 值最小.
将军饮马
【问题3】
在射线 上分别求点M、N,使△PMN 周长最小.
【问题4】
在射线 上分别求点M、N,使四边形PQMN
周长最小.
【问题5】
直线 m∥n ,在 m 、n上分别求点 M、N,
使MN⊥m ,且AM+MN+BN 的值最小.
造桥选址
【问题6】
在直线 上求两点M、N(M 在左),使 MN =a,
并使AM+MN+NB 的值最小.
【问题7】
A为 上一定点,B 为 上一定点,在 上求
点M,在 上求点 N ,使AM+MN+NB 的值最小.
【问题8】
在 上求点A,在 上求点 B,使 PA+AB 值最小.
【问题9】
△ABC 中每一内角都小于 120°,在△ABC 内求
一点P,使 PA+PB+PC 值最小.
费马点
【问题9】
费马点
解答:所求点为“费马点”,
即满足∠APB=∠BPC=∠ APC=120°.
以AB、AC为边向外作等边△ABD、△ACE,
连CD、BE 相交于P,点 P即为所求.
归纳小结
你有哪些收获快和伙伴们分享下吧
必做题:1.等腰△ABC中,CA=CB,M、N分别是两腰中点,在AB上找一点P,使得PM+PN最小。
2.直角坐标系中有正方形OABC,在OB上找一点P,使DP+AP最小。
选做题:
1.矩形ABCD中,AB=20厘米,BC=10厘米,若在AC、AB上各取一点M、N,使MB+MN值最小,求这个最小值。
2.已知定点A(1,2),B(3,4),在x轴找点P,使点P到A、B两点距离之和最短,求P点坐标。
课堂作业
敬请指导
谢 谢
同课章节目录
- 第一章 全等三角形
- 1.1 全等图形
- 1.2 全等三角形
- 1.3 探索三角形全等的条件
- 数学活动 关于三角形全等的条件
- 第二章 轴对称图形
- 2.1 轴对称与轴对称图形
- 2.2 轴对称的性质
- 2.3 设计轴对称图案
- 2.4 线段、角的轴对称性
- 2.5 等腰三角形的轴对称性
- 数学活动 折纸与证明
- 第三章 勾股定理
- 3.1 勾股定理
- 3.2 勾股定理的逆定理
- 3.3 勾股定理的简单应用
- 数学活动 探寻“勾股数”
- 第四章 实数
- 4.1 平方根
- 4.2 立方根
- 4.3 实数
- 4.4 近似数
- 数学活动 有关“实数”的课题探究
- 第五章 平面直角坐标系
- 5.1 物体位置的确定
- 5.2 平面直角坐标系
- 数学活动 确定藏宝地
- 第六章 一次函数
- 6.1 函数
- 6.2 一次函数
- 6.3 一次函数的图像
- 6.4 用一次函数解决问题
- 6.5 一次函数与二元一次方程
- 6.6 一次函数、一元一次方程和一元一次不等式
- 数学活动 温度计上的一次函数
