6.2 一次函数 课件(共25张PPT)
文档属性
| 名称 | 6.2 一次函数 课件(共25张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 993.2KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 鲁教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-10-20 06:46:31 | ||
图片预览





文档简介
(共25张PPT)
第六章 一次函数
2 一次函数
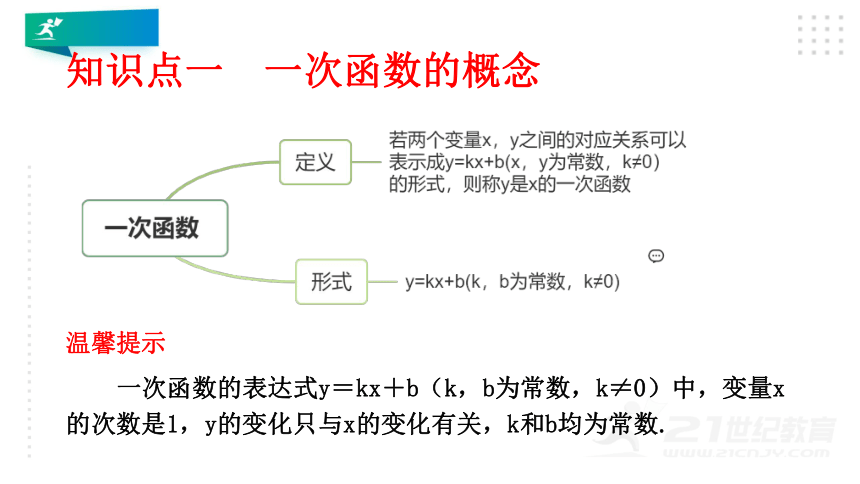
知识点一 一次函数的概念
知识点一 一次函数的概念
温馨提示
一次函数的表达式y=kx+b(k,b为常数,k≠0)中,变量x的次数是1,y的变化只与x的变化有关,k和b均为常数.
例1 在①y=-8x;②y=;③y=+1;④y=-8x2+6;
⑤y=-0.5x-1中,一次函数有( )
A.1个 B.2个 C.3个 D.4个
例1 在①y=-8x;②y=;③y=+1;④y=-8x2+6;
⑤y=-0.5x-1中,一次函数有( )
A.1个 B.2个 C.3个 D.4个
解析 由题意得,一次函数有①y=-8x;⑤y=-0.5x-1,共2个,故选B.
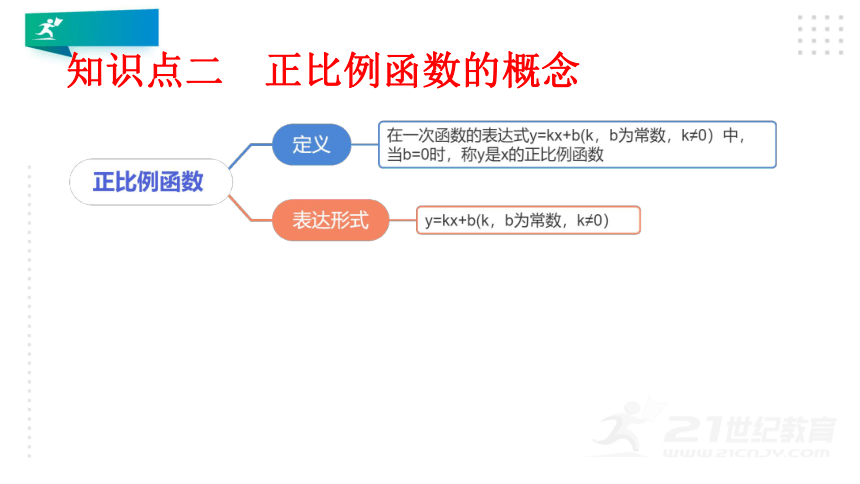
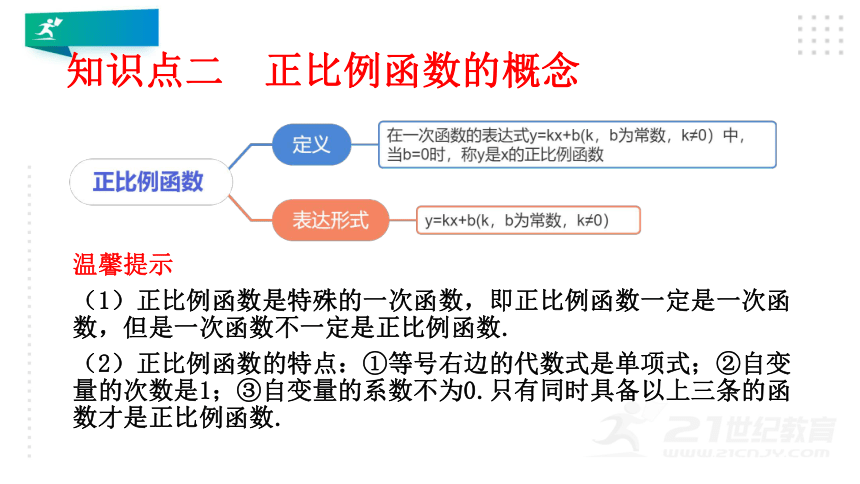
知识点二 正比例函数的概念
知识点二 正比例函数的概念
温馨提示
(1)正比例函数是特殊的一次函数,即正比例函数一定是一次函数,但是一次函数不一定是正比例函数.
(2)正比例函数的特点:①等号右边的代数式是单项式;②自变量的次数是1;③自变量的系数不为0.只有同时具备以上三条的函数才是正比例函数.
例2 下列y关于x的函数中,是正比例函数的为( )
A.y= B.y= C.y=x D.y=x+1
例2 下列y关于x的函数中,是正比例函数的为( )
A.y= B.y= C.y=x D.y=x+1
解析
判定 分析 综合点评
A不是 x2是关于x的二次式,所以y=x2不是正比例函数 辨别正比例函数,需明确以下三点:①自变量的次数为1;②常数项为0;③自变量的系数不等于0
B不是 y=不能化成y=kx(k≠0)的形式,所以y=不是正比例函数
C是 符合y=kx(k≠0)的一般形式
D不是 y=x+1不能化成y=kx(k≠0)的形式,所以y=x+1不是正比例函数
经典例题
题型一 根据一次函数或正比例函数的定义确定字母的取值
例1 函数y=(m-2)x+m2-4(m为常数).
(1)当m取何值时,y是x的正比例函数?
(2)当m取何值时,y是x的一次函数?
题型一 根据一次函数或正比例函数的定义确定字母的取值
例1 函数y=(m-2)x+m2-4(m为常数).
(1)当m取何值时,y是x的正比例函数?
(2)当m取何值时,y是x的一次函数?
解析 (1)当m2-4=0且m-2≠0时,y是x的正比例函数,此时m=-2.
(2)当m-2≠0,即m≠2时,y是x的一次函数.
题型一 根据一次函数或正比例函数的定义确定字母的取值
例1 函数y=(m-2)x+m2-4(m为常数).
(1)当m取何值时,y是x的正比例函数?
(2)当m取何值时,y是x的一次函数?
解析 (1)当m2-4=0且m-2≠0时,y是x的正比例函数,此时m=-2.
(2)当m-2≠0,即m≠2时,y是x的一次函数.
点拨 解此题的关键是掌握一次函数与正比例函数的定义:(1)一次函数y=kx+b的定义条件:k、b为常数,k≠0,自变量的次数为1;
(2)正比例函数y=kx的定义条件:k为常数且k≠0,自变量的次数为1.
题型二 一次函数关系的应用
题型二 一次函数关系的应用
例2 某公司销售玉米种子,价格为5元/千克,如果一次性购买10千克以上的种子,超过10千克部分的种子的价格打8折,部分表格如下:
(1)直接写出表格中a,b的值;
(2)设购买种子的数量为x(x>10)千克,付款金额为y元,求y与x的函数关系式;
(3)小李第一次购买种子35千克,第二次又购买了8千克,若两次购买种子的数量合在一起购买可省多少钱?
购买种子的数量/千克 2 5 10 12 20 30 …
付款金额/元 10 a 50 58 b 130 …
分析
(1)由题意计算可求解;
(2)由付款金额=10千克的金额+超过10千克部分的金额,可求y与x的函数关系式;
(3)分别求出两次购买金额,比较即可求解.
解析 (1)a=5×5=25,
b=5×10+(20-10)×0.8×5=90.
(2)y=5×10+5×0.8(x-10)=4x+10.
(3)购买35千克的付款金额=4×35+10=150(元),
购买8千克的付款金额=5×8=40(元),
一起购买的付款金额=4×(35+8)+10=182(元),
∴150+40-182=8(元),
答:一起购买可省8元.
易错易混
易错点 在判断函数是不是一次函数时,易忽略k≠0
易错点 在判断函数是不是一次函数时,易忽略k≠0
判断一个函数是不是一次函数,就是要通过恒等变形,看它能否转化为y=kx+b(k,b为常数,k≠0)的形式,若能,就是一次函数,若不能,就不是一次函数,解题过程中易忽略k≠0这个条件,导致出错.
例题 当k=________时,函数是关于x的一次函数.
例题 当k=________时,函数是关于x的一次函数.
解析 ∵函数y=是关于x的一次函数,
∴.k2-8=1,且k+3≠0.解得k=3.
故答案是3.
例题 当k=________时,函数是关于x的一次函数.
解析 ∵函数y=是关于x的一次函数,
∴.k2-8=1,且k+3≠0.解得k=3.
故答案是3.
易错分析
某函数是一次函数,除了要注意x的次数是1外,还要注意自变量x的系数≠0这个条件,本题易忽略k+3≠0,而得到错解k=±3.
第六章 一次函数
2 一次函数
知识点一 一次函数的概念
知识点一 一次函数的概念
温馨提示
一次函数的表达式y=kx+b(k,b为常数,k≠0)中,变量x的次数是1,y的变化只与x的变化有关,k和b均为常数.
例1 在①y=-8x;②y=;③y=+1;④y=-8x2+6;
⑤y=-0.5x-1中,一次函数有( )
A.1个 B.2个 C.3个 D.4个
例1 在①y=-8x;②y=;③y=+1;④y=-8x2+6;
⑤y=-0.5x-1中,一次函数有( )
A.1个 B.2个 C.3个 D.4个
解析 由题意得,一次函数有①y=-8x;⑤y=-0.5x-1,共2个,故选B.
知识点二 正比例函数的概念
知识点二 正比例函数的概念
温馨提示
(1)正比例函数是特殊的一次函数,即正比例函数一定是一次函数,但是一次函数不一定是正比例函数.
(2)正比例函数的特点:①等号右边的代数式是单项式;②自变量的次数是1;③自变量的系数不为0.只有同时具备以上三条的函数才是正比例函数.
例2 下列y关于x的函数中,是正比例函数的为( )
A.y= B.y= C.y=x D.y=x+1
例2 下列y关于x的函数中,是正比例函数的为( )
A.y= B.y= C.y=x D.y=x+1
解析
判定 分析 综合点评
A不是 x2是关于x的二次式,所以y=x2不是正比例函数 辨别正比例函数,需明确以下三点:①自变量的次数为1;②常数项为0;③自变量的系数不等于0
B不是 y=不能化成y=kx(k≠0)的形式,所以y=不是正比例函数
C是 符合y=kx(k≠0)的一般形式
D不是 y=x+1不能化成y=kx(k≠0)的形式,所以y=x+1不是正比例函数
经典例题
题型一 根据一次函数或正比例函数的定义确定字母的取值
例1 函数y=(m-2)x+m2-4(m为常数).
(1)当m取何值时,y是x的正比例函数?
(2)当m取何值时,y是x的一次函数?
题型一 根据一次函数或正比例函数的定义确定字母的取值
例1 函数y=(m-2)x+m2-4(m为常数).
(1)当m取何值时,y是x的正比例函数?
(2)当m取何值时,y是x的一次函数?
解析 (1)当m2-4=0且m-2≠0时,y是x的正比例函数,此时m=-2.
(2)当m-2≠0,即m≠2时,y是x的一次函数.
题型一 根据一次函数或正比例函数的定义确定字母的取值
例1 函数y=(m-2)x+m2-4(m为常数).
(1)当m取何值时,y是x的正比例函数?
(2)当m取何值时,y是x的一次函数?
解析 (1)当m2-4=0且m-2≠0时,y是x的正比例函数,此时m=-2.
(2)当m-2≠0,即m≠2时,y是x的一次函数.
点拨 解此题的关键是掌握一次函数与正比例函数的定义:(1)一次函数y=kx+b的定义条件:k、b为常数,k≠0,自变量的次数为1;
(2)正比例函数y=kx的定义条件:k为常数且k≠0,自变量的次数为1.
题型二 一次函数关系的应用
题型二 一次函数关系的应用
例2 某公司销售玉米种子,价格为5元/千克,如果一次性购买10千克以上的种子,超过10千克部分的种子的价格打8折,部分表格如下:
(1)直接写出表格中a,b的值;
(2)设购买种子的数量为x(x>10)千克,付款金额为y元,求y与x的函数关系式;
(3)小李第一次购买种子35千克,第二次又购买了8千克,若两次购买种子的数量合在一起购买可省多少钱?
购买种子的数量/千克 2 5 10 12 20 30 …
付款金额/元 10 a 50 58 b 130 …
分析
(1)由题意计算可求解;
(2)由付款金额=10千克的金额+超过10千克部分的金额,可求y与x的函数关系式;
(3)分别求出两次购买金额,比较即可求解.
解析 (1)a=5×5=25,
b=5×10+(20-10)×0.8×5=90.
(2)y=5×10+5×0.8(x-10)=4x+10.
(3)购买35千克的付款金额=4×35+10=150(元),
购买8千克的付款金额=5×8=40(元),
一起购买的付款金额=4×(35+8)+10=182(元),
∴150+40-182=8(元),
答:一起购买可省8元.
易错易混
易错点 在判断函数是不是一次函数时,易忽略k≠0
易错点 在判断函数是不是一次函数时,易忽略k≠0
判断一个函数是不是一次函数,就是要通过恒等变形,看它能否转化为y=kx+b(k,b为常数,k≠0)的形式,若能,就是一次函数,若不能,就不是一次函数,解题过程中易忽略k≠0这个条件,导致出错.
例题 当k=________时,函数是关于x的一次函数.
例题 当k=________时,函数是关于x的一次函数.
解析 ∵函数y=是关于x的一次函数,
∴.k2-8=1,且k+3≠0.解得k=3.
故答案是3.
例题 当k=________时,函数是关于x的一次函数.
解析 ∵函数y=是关于x的一次函数,
∴.k2-8=1,且k+3≠0.解得k=3.
故答案是3.
易错分析
某函数是一次函数,除了要注意x的次数是1外,还要注意自变量x的系数≠0这个条件,本题易忽略k+3≠0,而得到错解k=±3.
