冀教版数学八年级下册第20章达标测试卷(word版含答案)
文档属性
| 名称 | 冀教版数学八年级下册第20章达标测试卷(word版含答案) |  | |
| 格式 | doc | ||
| 文件大小 | 303.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 冀教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-10-20 09:35:11 | ||
图片预览


文档简介
第二十章达标测试卷
一、选择题(每题2分,共28分)
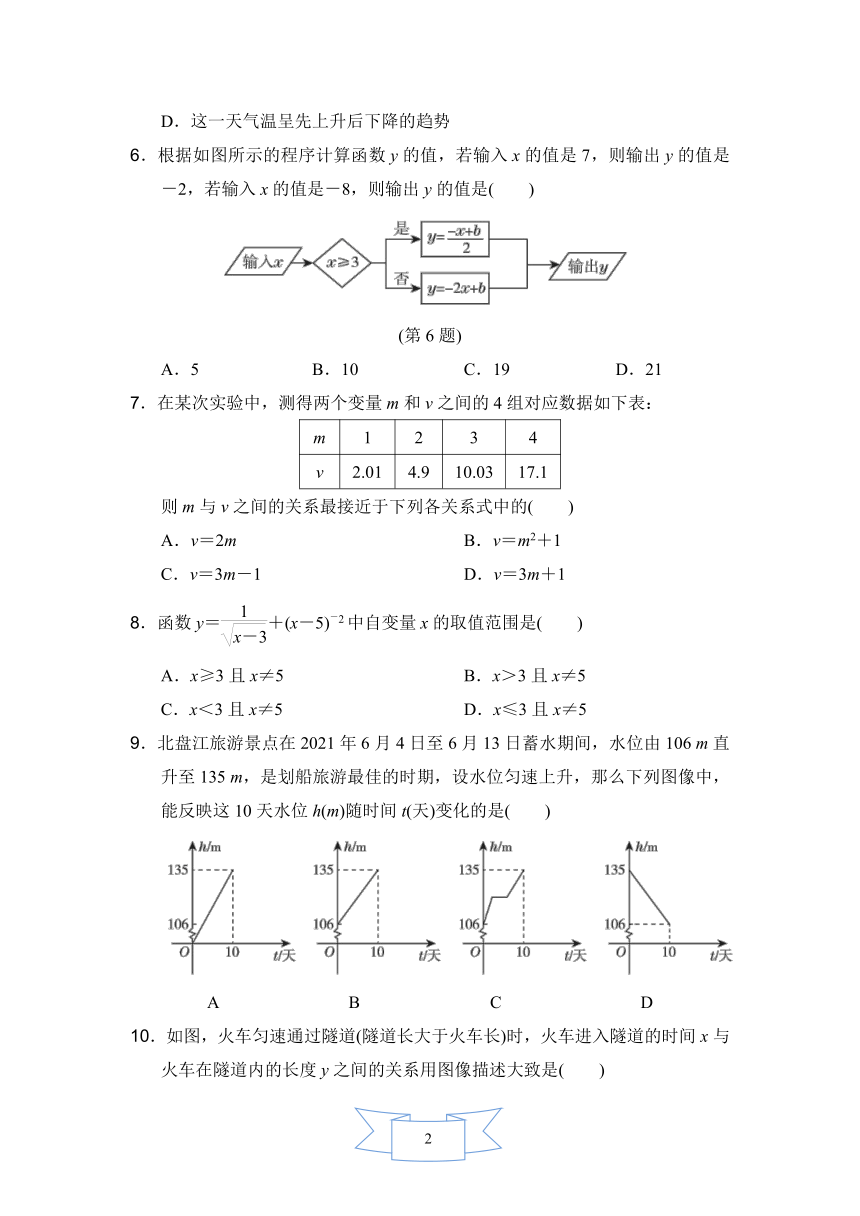
1.下列图像中,不能表示y是x的函数的是( )
A B C D
2.在正方形的周长公式C=4a中,常量与变量分别是( )
A.4,a是常量,C是变量 B.4是常量,C,a是变量
C.a是常量,4是变量 D.C是常量,4,a是变量
3.如图,l1反映了某公司的销售收入(单位:元)与销售量(单位:吨)的关系,l2反映了该公司的销售成本(单位:元)与销售量(单位:吨)的关系,当该公司盈利(收入大于成本)时,销售量应为( )
A.大于4吨 B.等于5吨 C.小于5吨 D.大于5吨
(第3题) (第5题)
4.下列关于变量x和y的关系式:x-y=0,y2=x,|y|=2x,y2=x2,y=3-x,y=2x2-1,y=,其中y是x的函数的个数为( )
A.3 B.4 C.5 D.6
5.如图是自动测温仪记录的图像,它反映了武汉的冬季某天气温T随时间t的变化而变化的情况,下列说法错误的是( )
A.这一天4时气温最低
B.这一天14时气温最高
C.从4时至14时气温呈上升趋势(即气温随时间增长而上升)
D.这一天气温呈先上升后下降的趋势
6.根据如图所示的程序计算函数y的值,若输入x的值是7,则输出y的值是-2,若输入x的值是-8,则输出y的值是( )
(第6题)
A.5 B.10 C.19 D.21
7.在某次实验中,测得两个变量m和v之间的4组对应数据如下表:
m 1 2 3 4
v 2.01 4.9 10.03 17.1
则m与v之间的关系最接近于下列各关系式中的( )
A.v=2m B.v=m2+1
C.v=3m-1 D.v=3m+1
8.函数y=+(x-5)-2中自变量x的取值范围是( )
A.x≥3且x≠5 B.x>3且x≠5
C.x<3且x≠5 D.x≤3且x≠5
9.北盘江旅游景点在2021年6月4日至6月13日蓄水期间,水位由106 m直升至135 m,是划船旅游最佳的时期,设水位匀速上升,那么下列图像中,能反映这10天水位h(m)随时间t(天)变化的是( )
A B C D
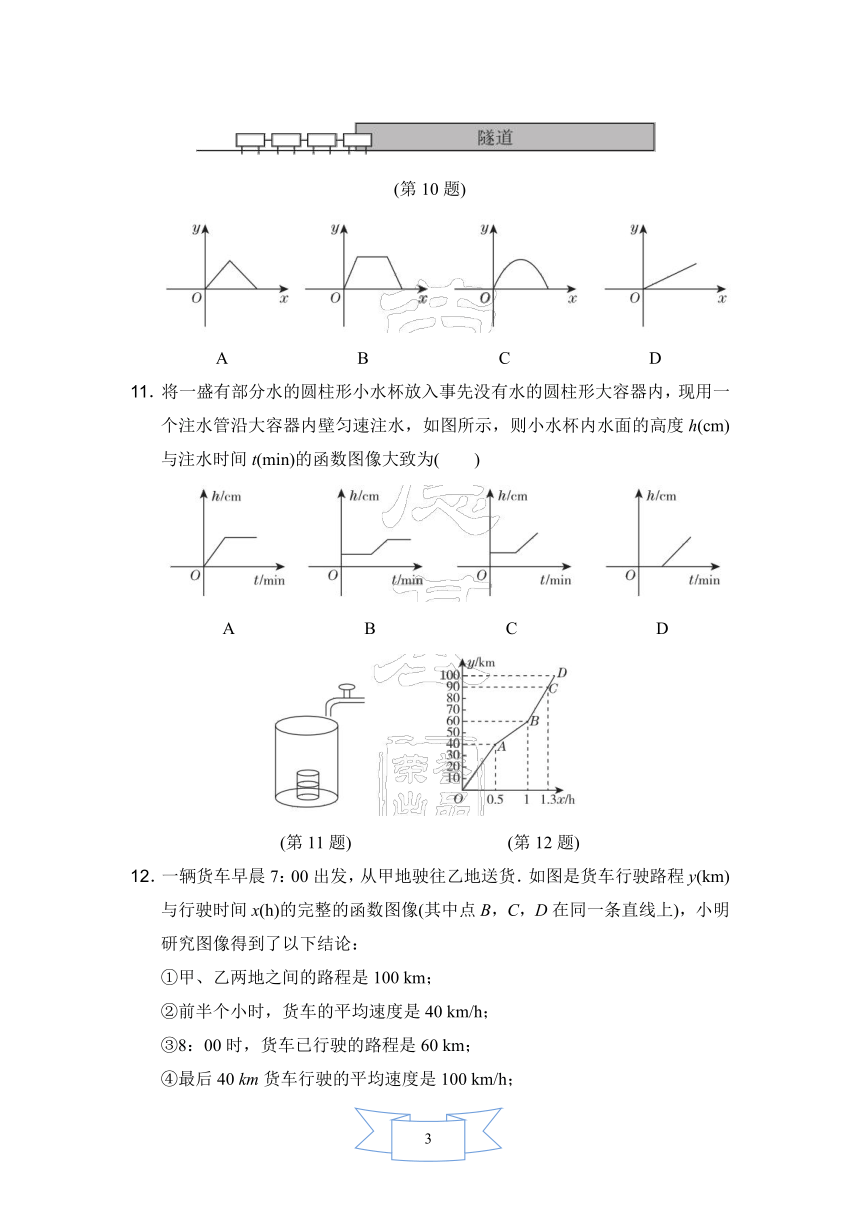
10.如图,火车匀速通过隧道(隧道长大于火车长)时,火车进入隧道的时间x与火车在隧道内的长度y之间的关系用图像描述大致是( )
(第10题)
A B C D
11.将一盛有部分水的圆柱形小水杯放入事先没有水的圆柱形大容器内,现用一个注水管沿大容器内壁匀速注水,如图所示,则小水杯内水面的高度h(cm)与注水时间t(min)的函数图像大致为( )
A B C D
(第11题) (第12题)
12.一辆货车早晨7:00出发,从甲地驶往乙地送货.如图是货车行驶路程y(km)与行驶时间x(h)的完整的函数图像(其中点B,C,D在同一条直线上),小明研究图像得到了以下结论:
①甲、乙两地之间的路程是100 km;
②前半个小时,货车的平均速度是40 km/h;
③8:00时,货车已行驶的路程是60 km;
④最后40 km货车行驶的平均速度是100 km/h;
⑤货车到达乙地的时间是8:24.
其中正确的结论是( )
A.①②③④ B.①③⑤
C.①③④ D.①③④⑤
13.如图①,在长方形MNPQ中,动点R从点N出发,沿N→P→Q→M方向运动至点M处停止.设点R运动的路程为x,图中阴影部分△MNR的面积为y,如果y关于x的函数图像如图②所示,则长方形MNPQ的面积为( )
(第13题)
A.16 B.20 C.36 D.45
14.如图甲,点G为BC边的中点,点H在AF上,动点P以每秒2 cm的速度沿路线G→C→D→E→F→H运动,到点H停止,相应的△ABP的面积y(cm2)关于点P的运动时间t(s)的函数图像如图乙所示.若AB=6 cm,则下列结论正确的个数是( )
①图甲中BC的长是4 cm;②图甲中DE的长是6 cm;
③图乙中点M表示4 s时y的值为24;
④图乙中点N表示12 s时y的值为15.
(第14题)
A.4 B.3 C.2 D.1
二、填空题(每题3分,共12分)
15.在函数y=中,自变量x的取值范围是______________.
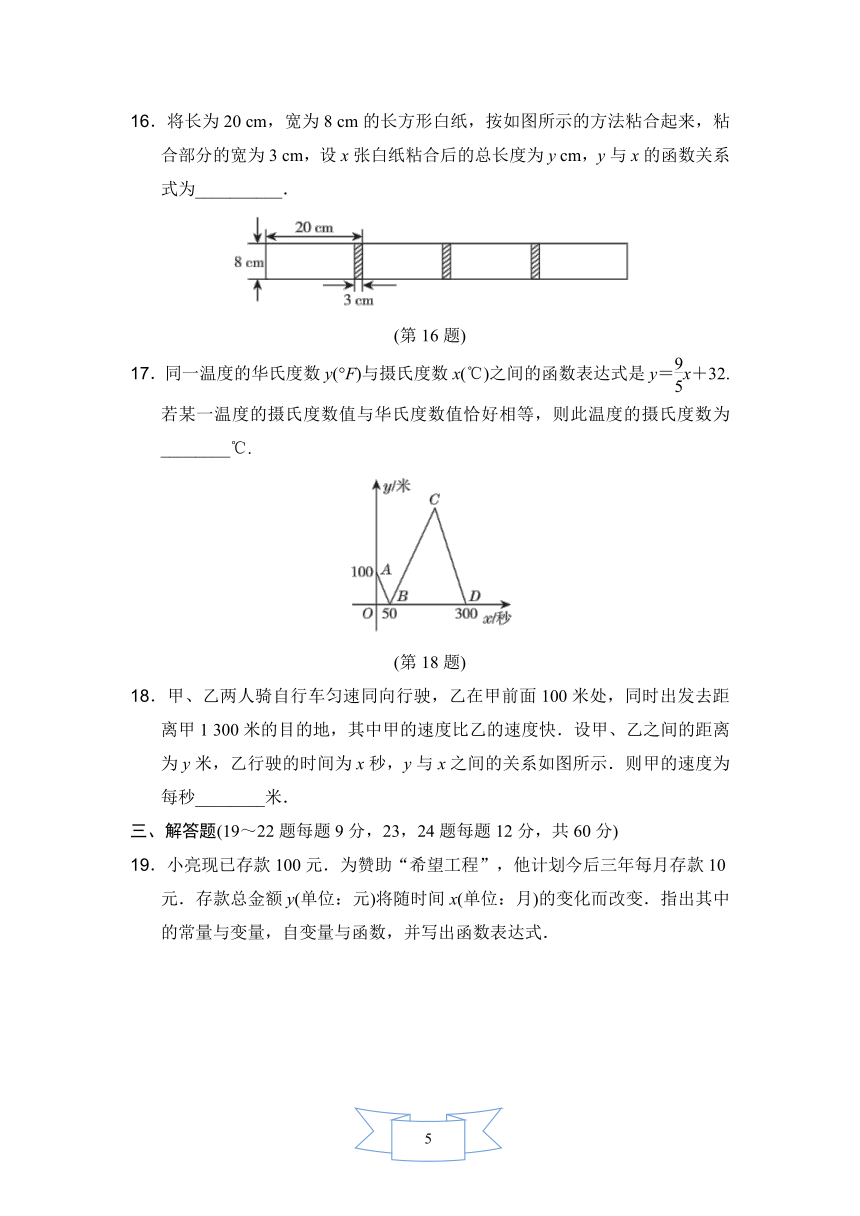
16.将长为20 cm,宽为8 cm的长方形白纸,按如图所示的方法粘合起来,粘合部分的宽为3 cm,设x张白纸粘合后的总长度为y cm,y与x的函数关系式为__________.
(第16题)
17.同一温度的华氏度数y(°F)与摄氏度数x(℃)之间的函数表达式是y=x+32.若某一温度的摄氏度数值与华氏度数值恰好相等,则此温度的摄氏度数为________℃.
(第18题)
18.甲、乙两人骑自行车匀速同向行驶,乙在甲前面100米处,同时出发去距离甲1 300米的目的地,其中甲的速度比乙的速度快.设甲、乙之间的距离为y米,乙行驶的时间为x秒,y与x之间的关系如图所示.则甲的速度为每秒________米.
三、解答题(19~22题每题9分,23,24题每题12分,共60分)
19.小亮现已存款100元.为赞助“希望工程”,他计划今后三年每月存款10元.存款总金额y(单位:元)将随时间x(单位:月)的变化而改变.指出其中的常量与变量,自变量与函数,并写出函数表达式.
20.某医药研究所研发了一种新药,在检测药效时发现,如果成人按规定剂量服用,那么每毫升血液中含药量y(微克)随时间x(小时)的变化情况如图所示,根据图像回答下列问题:
(1)服药后几小时,血液中含药量最高?每毫升血液中含药量是多少微克?
(2)服药后14小时血液中含药量是多少微克?
(3)在服药后几小时之内,血液中含药量逐渐升高?在几小时后,血液中含药量逐渐下降?
(4)服药几小时后即无药效?
(第20题)
21.观察下图,然后回答问题.
(1)由上而下第8行,白球有________个,黑球有________个;
(2)若由上而下第n行白球与黑球的总数为y个,则y与n的关系式为______________________________;
(3)请你求出由上而下第2 022行白球和黑球的总数.
(第21题)
22.某学校团支部书记暑假带领该校“优等生”去旅游,甲旅行社说:“若团支部书记买一张全票,则学生可享受半价优惠.”乙旅行社说:“包括团支部书记在内都享受六折优惠.”若全票票价是1 200元,设学生人数为x,甲旅行社收费为y甲、乙旅行社收费为y乙.
(1)分别写出两家旅行社的收费与学生人数的关系式;
(2)当学生人数是多少时,两家旅行社的收费是一样的?
(3)就学生人数讨论哪家旅行社更优惠.
23.王叔叔在批发市场按每千克1.8元批发了若干千克西瓜进城出售,为了方便,他带了一些零钱备用.他先按市场价售出一些后,又降价出售.售出西瓜质量x(千克)与他手中的钱数y(元)(含备用零钱)的关系如图所示,结合图像回答下列问题:
(1)他自带的零钱是多少?
(2)降价前他每千克西瓜出售的价格是多少?
(3)随后他按每千克的价格下降0.5元将剩余的西瓜售完,这时他手中的钱(含备用零钱)是390元,他一共批发了多少千克西瓜?
(4)他一共赚了多少钱?
(第23题)
24.今年我市对城区内的老旧小区进行升级改造,某小区准备修建一条长1 350米的健身小路.甲、乙两个工程队想承建这项工程,经了解得到了如下表所示的信息:
工程队 每天修路的长度/米 单独完成所需天数/天 每天所需费用/元
甲队 50 m 800
乙队 n m+18 640
(1)m=________,n=________;
(2)甲队先修了x米之后,甲、乙两队一起修,又用了y天完成这项工程.
①当x=150时,求出乙队修路的天数;
②求y与x之间的函数关系式(不用写出x的取值范围);
③若总费用不超过23 000元,求甲队至少先修了多少米.
答案
一、1.B 2.B 3.D 4.B 5.D
6.C 7.B 8.B 9.B 10.B
11.B 12.D 13.B 14.C
二、15.x≥-1且x≠0 16.y=17x+3
17.-40 18.6
三、19.解:由题意得,常量为100,10,变量为x,y,自变量为x,y是x的函数,表达式为y=10x+100(0≤x≤36,x是整数).
20.解:(1)由函数图像得服药后2小时,血液中含药量最高,每毫升血液中含药量是6微克.
(2)由函数图像得服药后14小时血液中含药量是2微克.
(3)由函数图像得在服药后2小时之内,血液中含药量逐渐升高,在2小时后,血液中含药量逐渐下降.
(4)由函数图像得服药20小时后即无药效.
21.解:(1)8;15 (2)y=3n-1
(3)把n=2 022代入y=3n-1,
得y=6 065.
所以由上而下第2 022行白球和黑球的总数为6 065个.
22.解:(1)由题意,得
y甲=0.5×1 200x+1 200=600x+1 200,
y乙=0.6×1 200x+0.6×1 200=720x+720.
(2)当y甲=y乙时,
600x+1 200=720x+720,
解得x=4,
故当学生人数是4人时,两家旅行社的收费是一样的.
(3)当y甲>y乙时,
600x+1 200>720x+720,
解得x<4;
当y甲<y乙时,
600x+1 200<720x+720,
解得x>4.
故当0<x<4(x为整数)时,乙旅行社更优惠;
当x>4(x为整数)时,甲旅行社更优惠.
23.解:(1)由图像可得王叔叔自带的零钱为50元.
(2)(290-50)÷80=3(元),
答:降价前他每千克西瓜出售的价格是3元.
(3)(390-290)÷(3-0.5)=40(千克),80+40=120(千克),
答:他一共批发了120千克西瓜.
(4)390-120×1.8-50=124(元),
答:他一共赚了124元钱.
24.解:(1)27;30
(2)①乙队修路的天数为=15(天).
②由题意,得x+(30+50)y=1 350,
∴y与x之间的函数关系式为y=-x+.
③由题意,得:800×+(800+640)≤23 000,
解得x≥650,
答:甲队至少先修了650米.
一、选择题(每题2分,共28分)
1.下列图像中,不能表示y是x的函数的是( )
A B C D
2.在正方形的周长公式C=4a中,常量与变量分别是( )
A.4,a是常量,C是变量 B.4是常量,C,a是变量
C.a是常量,4是变量 D.C是常量,4,a是变量
3.如图,l1反映了某公司的销售收入(单位:元)与销售量(单位:吨)的关系,l2反映了该公司的销售成本(单位:元)与销售量(单位:吨)的关系,当该公司盈利(收入大于成本)时,销售量应为( )
A.大于4吨 B.等于5吨 C.小于5吨 D.大于5吨
(第3题) (第5题)
4.下列关于变量x和y的关系式:x-y=0,y2=x,|y|=2x,y2=x2,y=3-x,y=2x2-1,y=,其中y是x的函数的个数为( )
A.3 B.4 C.5 D.6
5.如图是自动测温仪记录的图像,它反映了武汉的冬季某天气温T随时间t的变化而变化的情况,下列说法错误的是( )
A.这一天4时气温最低
B.这一天14时气温最高
C.从4时至14时气温呈上升趋势(即气温随时间增长而上升)
D.这一天气温呈先上升后下降的趋势
6.根据如图所示的程序计算函数y的值,若输入x的值是7,则输出y的值是-2,若输入x的值是-8,则输出y的值是( )
(第6题)
A.5 B.10 C.19 D.21
7.在某次实验中,测得两个变量m和v之间的4组对应数据如下表:
m 1 2 3 4
v 2.01 4.9 10.03 17.1
则m与v之间的关系最接近于下列各关系式中的( )
A.v=2m B.v=m2+1
C.v=3m-1 D.v=3m+1
8.函数y=+(x-5)-2中自变量x的取值范围是( )
A.x≥3且x≠5 B.x>3且x≠5
C.x<3且x≠5 D.x≤3且x≠5
9.北盘江旅游景点在2021年6月4日至6月13日蓄水期间,水位由106 m直升至135 m,是划船旅游最佳的时期,设水位匀速上升,那么下列图像中,能反映这10天水位h(m)随时间t(天)变化的是( )
A B C D
10.如图,火车匀速通过隧道(隧道长大于火车长)时,火车进入隧道的时间x与火车在隧道内的长度y之间的关系用图像描述大致是( )
(第10题)
A B C D
11.将一盛有部分水的圆柱形小水杯放入事先没有水的圆柱形大容器内,现用一个注水管沿大容器内壁匀速注水,如图所示,则小水杯内水面的高度h(cm)与注水时间t(min)的函数图像大致为( )
A B C D
(第11题) (第12题)
12.一辆货车早晨7:00出发,从甲地驶往乙地送货.如图是货车行驶路程y(km)与行驶时间x(h)的完整的函数图像(其中点B,C,D在同一条直线上),小明研究图像得到了以下结论:
①甲、乙两地之间的路程是100 km;
②前半个小时,货车的平均速度是40 km/h;
③8:00时,货车已行驶的路程是60 km;
④最后40 km货车行驶的平均速度是100 km/h;
⑤货车到达乙地的时间是8:24.
其中正确的结论是( )
A.①②③④ B.①③⑤
C.①③④ D.①③④⑤
13.如图①,在长方形MNPQ中,动点R从点N出发,沿N→P→Q→M方向运动至点M处停止.设点R运动的路程为x,图中阴影部分△MNR的面积为y,如果y关于x的函数图像如图②所示,则长方形MNPQ的面积为( )
(第13题)
A.16 B.20 C.36 D.45
14.如图甲,点G为BC边的中点,点H在AF上,动点P以每秒2 cm的速度沿路线G→C→D→E→F→H运动,到点H停止,相应的△ABP的面积y(cm2)关于点P的运动时间t(s)的函数图像如图乙所示.若AB=6 cm,则下列结论正确的个数是( )
①图甲中BC的长是4 cm;②图甲中DE的长是6 cm;
③图乙中点M表示4 s时y的值为24;
④图乙中点N表示12 s时y的值为15.
(第14题)
A.4 B.3 C.2 D.1
二、填空题(每题3分,共12分)
15.在函数y=中,自变量x的取值范围是______________.
16.将长为20 cm,宽为8 cm的长方形白纸,按如图所示的方法粘合起来,粘合部分的宽为3 cm,设x张白纸粘合后的总长度为y cm,y与x的函数关系式为__________.
(第16题)
17.同一温度的华氏度数y(°F)与摄氏度数x(℃)之间的函数表达式是y=x+32.若某一温度的摄氏度数值与华氏度数值恰好相等,则此温度的摄氏度数为________℃.
(第18题)
18.甲、乙两人骑自行车匀速同向行驶,乙在甲前面100米处,同时出发去距离甲1 300米的目的地,其中甲的速度比乙的速度快.设甲、乙之间的距离为y米,乙行驶的时间为x秒,y与x之间的关系如图所示.则甲的速度为每秒________米.
三、解答题(19~22题每题9分,23,24题每题12分,共60分)
19.小亮现已存款100元.为赞助“希望工程”,他计划今后三年每月存款10元.存款总金额y(单位:元)将随时间x(单位:月)的变化而改变.指出其中的常量与变量,自变量与函数,并写出函数表达式.
20.某医药研究所研发了一种新药,在检测药效时发现,如果成人按规定剂量服用,那么每毫升血液中含药量y(微克)随时间x(小时)的变化情况如图所示,根据图像回答下列问题:
(1)服药后几小时,血液中含药量最高?每毫升血液中含药量是多少微克?
(2)服药后14小时血液中含药量是多少微克?
(3)在服药后几小时之内,血液中含药量逐渐升高?在几小时后,血液中含药量逐渐下降?
(4)服药几小时后即无药效?
(第20题)
21.观察下图,然后回答问题.
(1)由上而下第8行,白球有________个,黑球有________个;
(2)若由上而下第n行白球与黑球的总数为y个,则y与n的关系式为______________________________;
(3)请你求出由上而下第2 022行白球和黑球的总数.
(第21题)
22.某学校团支部书记暑假带领该校“优等生”去旅游,甲旅行社说:“若团支部书记买一张全票,则学生可享受半价优惠.”乙旅行社说:“包括团支部书记在内都享受六折优惠.”若全票票价是1 200元,设学生人数为x,甲旅行社收费为y甲、乙旅行社收费为y乙.
(1)分别写出两家旅行社的收费与学生人数的关系式;
(2)当学生人数是多少时,两家旅行社的收费是一样的?
(3)就学生人数讨论哪家旅行社更优惠.
23.王叔叔在批发市场按每千克1.8元批发了若干千克西瓜进城出售,为了方便,他带了一些零钱备用.他先按市场价售出一些后,又降价出售.售出西瓜质量x(千克)与他手中的钱数y(元)(含备用零钱)的关系如图所示,结合图像回答下列问题:
(1)他自带的零钱是多少?
(2)降价前他每千克西瓜出售的价格是多少?
(3)随后他按每千克的价格下降0.5元将剩余的西瓜售完,这时他手中的钱(含备用零钱)是390元,他一共批发了多少千克西瓜?
(4)他一共赚了多少钱?
(第23题)
24.今年我市对城区内的老旧小区进行升级改造,某小区准备修建一条长1 350米的健身小路.甲、乙两个工程队想承建这项工程,经了解得到了如下表所示的信息:
工程队 每天修路的长度/米 单独完成所需天数/天 每天所需费用/元
甲队 50 m 800
乙队 n m+18 640
(1)m=________,n=________;
(2)甲队先修了x米之后,甲、乙两队一起修,又用了y天完成这项工程.
①当x=150时,求出乙队修路的天数;
②求y与x之间的函数关系式(不用写出x的取值范围);
③若总费用不超过23 000元,求甲队至少先修了多少米.
答案
一、1.B 2.B 3.D 4.B 5.D
6.C 7.B 8.B 9.B 10.B
11.B 12.D 13.B 14.C
二、15.x≥-1且x≠0 16.y=17x+3
17.-40 18.6
三、19.解:由题意得,常量为100,10,变量为x,y,自变量为x,y是x的函数,表达式为y=10x+100(0≤x≤36,x是整数).
20.解:(1)由函数图像得服药后2小时,血液中含药量最高,每毫升血液中含药量是6微克.
(2)由函数图像得服药后14小时血液中含药量是2微克.
(3)由函数图像得在服药后2小时之内,血液中含药量逐渐升高,在2小时后,血液中含药量逐渐下降.
(4)由函数图像得服药20小时后即无药效.
21.解:(1)8;15 (2)y=3n-1
(3)把n=2 022代入y=3n-1,
得y=6 065.
所以由上而下第2 022行白球和黑球的总数为6 065个.
22.解:(1)由题意,得
y甲=0.5×1 200x+1 200=600x+1 200,
y乙=0.6×1 200x+0.6×1 200=720x+720.
(2)当y甲=y乙时,
600x+1 200=720x+720,
解得x=4,
故当学生人数是4人时,两家旅行社的收费是一样的.
(3)当y甲>y乙时,
600x+1 200>720x+720,
解得x<4;
当y甲<y乙时,
600x+1 200<720x+720,
解得x>4.
故当0<x<4(x为整数)时,乙旅行社更优惠;
当x>4(x为整数)时,甲旅行社更优惠.
23.解:(1)由图像可得王叔叔自带的零钱为50元.
(2)(290-50)÷80=3(元),
答:降价前他每千克西瓜出售的价格是3元.
(3)(390-290)÷(3-0.5)=40(千克),80+40=120(千克),
答:他一共批发了120千克西瓜.
(4)390-120×1.8-50=124(元),
答:他一共赚了124元钱.
24.解:(1)27;30
(2)①乙队修路的天数为=15(天).
②由题意,得x+(30+50)y=1 350,
∴y与x之间的函数关系式为y=-x+.
③由题意,得:800×+(800+640)≤23 000,
解得x≥650,
答:甲队至少先修了650米.
同课章节目录
- 第十八章 数据的收集与整理
- 18.1 统计的初步认识
- 18.2 抽样调查
- 18.3 数据的整理与表示
- 18.4 频数分布表与直方图
- 第十九章 平面直角坐标系
- 19.1 确定平面上物体的位置
- 19.2 平面直角坐标系
- 19.3 坐标与图形的位置
- 19.4 坐标与图形的变化
- 第二十章 函数
- 20.1 常量和变量
- 20.2 函数
- 20.3 函数的表示
- 20.4 函数的初步应用
- 第二十一章 一次函数
- 21.1 一次函数
- 21.2 一次函数的图像和性质
- 21.3 用待定系数法确定一次函数表达式
- 21.4 一次函数的应用
- 21.5 一次函数与二元一次方程的关系
- 第二十二章 四边形
- 22.1 平行四边形的性质
- 22.2 平行四边形的判断
- 22.3 三角形的中位线
- 22.4 矩形
- 22.5 菱形
- 22.6 正方形
- 22.7 多边形的内角和与外角和
