冀教版数学八年级下册 第22章达标测试卷(word版含答案)
文档属性
| 名称 | 冀教版数学八年级下册 第22章达标测试卷(word版含答案) |  | |
| 格式 | doc | ||
| 文件大小 | 340.2KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 冀教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-10-20 09:38:39 | ||
图片预览



文档简介
第二十二章达标测试卷
一、选择题(每题2分,共28分)
1.在 ABCD中,∠A+∠C=200°,则∠A的度数为( )
A.130° B.100° C.80° D.70°
2.已知一个多边形的内角和等于900°,则这个多边形是( )
A.五边形 B.六边形 C.七边形 D.八边形
3.如图, ABCD中,对角线AC,BD交于点O,点E是BC的中点.若OE=3 cm,则AB的长为( )
A.12 cm B.9 cm C.6 cm D.3 cm
(第3题) (第4题)
4.如图,点A是直线l外一点,在l上取两点B,C,分别以A,C为圆心,BC,AB长为半径画弧,两弧相交于点D,分别连接AB,AD,CD,则四边形ABCD的( )
A.四条边相等 B.四个角相等
C.对角线互相垂直 D.对角线互相平分
5.如图,已知在菱形ABCD中,对角线AC与BD交于点O,∠BAD=120°,AC=4,则该菱形的面积是( )
(第5题)
A.16 B.16 C.8 D.8
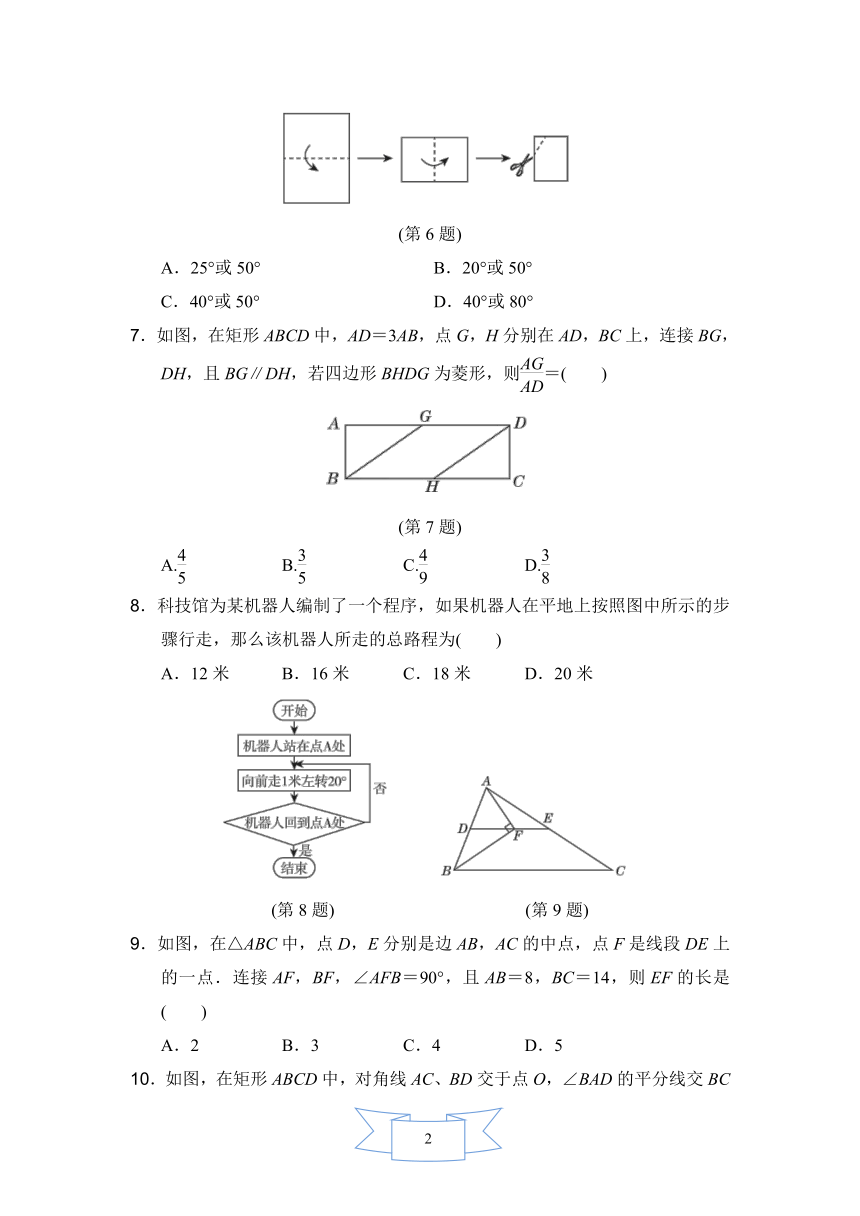
6.如图,把一张长方形纸片对折两次,然后剪下一个角,为了得到一个钝角为100°的菱形,裁剪线与第二条折痕所成的夹角度数为( )
(第6题)
A.25°或50° B.20°或50°
C.40°或50° D.40°或80°
7.如图,在矩形ABCD中,AD=3AB,点G,H分别在AD,BC上,连接BG,DH,且BG∥DH,若四边形BHDG为菱形,则=( )
(第7题)
A. B. C. D.
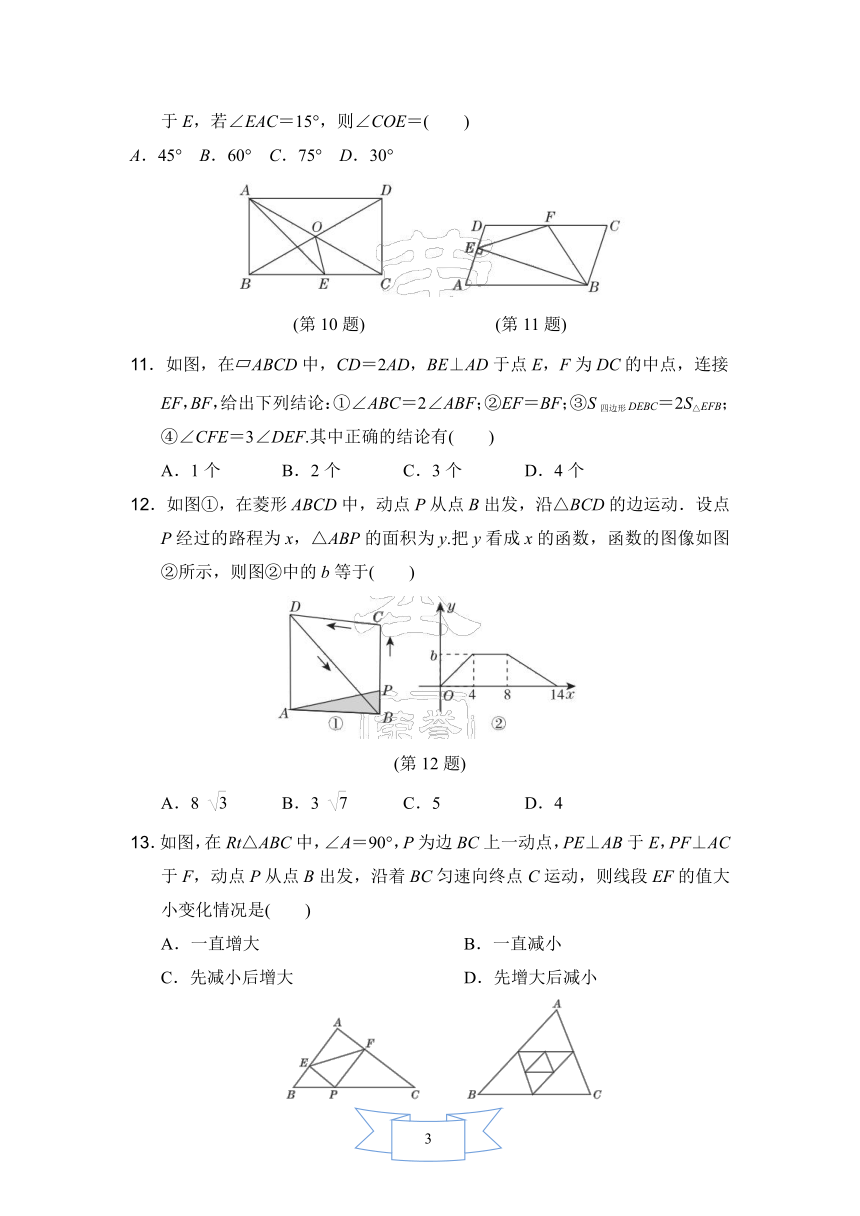
8.科技馆为某机器人编制了一个程序,如果机器人在平地上按照图中所示的步骤行走,那么该机器人所走的总路程为( )
A.12米 B.16米 C.18米 D.20米
(第8题) (第9题)
9.如图,在△ABC中,点D,E分别是边AB,AC的中点,点F是线段DE上的一点.连接AF,BF,∠AFB=90°,且AB=8,BC=14,则EF的长是( )
A.2 B.3 C.4 D.5
10.如图,在矩形ABCD中,对角线AC、BD交于点O,∠BAD的平分线交BC于E,若∠EAC=15°,则∠COE=( )
A.45° B.60° C.75° D.30°
(第10题) (第11题)
11.如图,在 ABCD中,CD=2AD,BE⊥AD于点E,F为DC的中点,连接EF,BF,给出下列结论:①∠ABC=2∠ABF;②EF=BF;③S四边形DEBC=2S△EFB;④∠CFE=3∠DEF.其中正确的结论有( )
A.1个 B.2个 C.3个 D.4个
12.如图①,在菱形ABCD中,动点P从点B出发,沿△BCD的边运动.设点P经过的路程为x,△ABP的面积为y.把y看成x的函数,函数的图像如图②所示,则图②中的b等于( )
(第12题)
A.8 B.3 C.5 D.4
13.如图,在Rt△ABC中,∠A=90°,P为边BC上一动点,PE⊥AB于E,PF⊥AC于F,动点P从点B出发,沿着BC匀速向终点C运动,则线段EF的值大小变化情况是( )
A.一直增大 B.一直减小
C.先减小后增大 D.先增大后减小
(第13题) (第14题)
14.如图,已知△ABC的周长为1,连接△ABC三边的中点构成第二个三角形,再连接第二个三角形三边中点构成第三个三角形,依此类推,则第2 022个三角形的周长是( )
A. B. C. D.
二、填空题(共4小题,每题3分,共12分)
15.如图,四边形ABCD是菱形,点O是两条对角线的交点,过点O的三条直线将菱形分成阴影和空白部分,当菱形的两条对角线长分别为12和16时,则阴影部分面积为________.
(第15题) (第16题)
16.如图,在四边形ABCD中,点P是对角线BD的中点,点E、F分别是AB、CD的中点,AD=BC,∠PEF=30°,则∠EPF的度数是________.
17.如图,BD为正方形ABCD的对角线,BE平分∠DBC,交DC于点E,延长BC到F,使CF=CE,连接DF.若CE=1 cm,则BF=________.
(第17题)
18.菱形OBCD在平面直角坐标系中的位置如图所示,顶点B(2,0),∠DOB=60°,点P是对角线OC上一个动点,E,则EP+BP的最小值为________,此时点P的坐标为________.
(第18题)
三、解答题(19~22题每题9分,23、24题每题12分,共60分)
19.(1)已知一个正多边形的每个内角比它的每个外角的4倍多30°,求这个多边形的边数;
(2)一个多边形的外角和是内角和的,求这个多边形的边数.
20.如图,在 ABCD中,点E,F分别在边CB,AD的延长线上,且BE=DF,连接EF,分别与AB,CD交于点G,H.
求证:AG=CH.
(第20题)
21.如图,△ABC中,AB=AC,AD平分∠BAC,点O为AB的中点,连接DO并延长到点E,使OE=OD,连接AE,BE.
(1)求证:四边形AEBD是矩形;
(2)当△ABC满足什么条件时,矩形AEBD是正方形,并说明理由.
(第21题)
22.如图,正方形ABCD中,E,F分别是AB,BC边上的点,AF与DE相交于点G,且AF=DE.求证:
(1)BF=AE;
(2)AF⊥DE.
(第22题)
23.如图,△ABC中,∠ACB=90°,D为AB的中点,四边形BCED为平行四边形,DE,AC相交于F.连接DC,AE.
(1)试确定四边形ADCE的形状,并说明理由;
(2)若AB=16,AC=12,求四边形ADCE的面积;
(3)当△ABC满足什么条件时,四边形ADCE为正方形?请给予证明.
(第23题)
24.(1)如图①,矩形ABCD的对角线AC、BD交于点O,过点C作BD的平行线,过点D作AC的平行线,两线交于点P,则四边形CODP的形状是________;
(2)如图②,若(1)中的矩形变为菱形,其他条件不变,则四边形CODP的形状是________;
(3)如图③,若(1)中的矩形变为正方形,其他条件不变,请判断四边形CODP的形状,并说明理由.
(第24题)
答案
一、1.B 2.C 3.C 4.D 5.C 6.C
7.C 点拨:设AB=1,则AD=3.若四边形BHDG为菱形,则BG=GD.设BG=GD=x,则AG=3-x.在Rt△ABG中,12+=x2 ,解得x= ,所以==.
8.C 9.B 10.A
11.D 点拨:∵在 ABCD中,CD=2AD,F为DC的中点,∴CF=CD=AD=BC,∴∠CBF=∠CFB.
∵AB∥CD,∴∠CFB=∠ABF.
∴∠CBF=∠ABF.∴∠ABC=∠ABF+∠CBF=2∠ABF.故①正确.
如图,延长EF,BC,相交于点G.
(第11题)
易证得△DEF≌△CGF,∴FE=FG.
∵BE⊥AD,AD∥BC,∴∠EBG=90°.
根据直角三角形斜边上的中线等于斜边的一半得,EF=BF,故②正确.
∵BF是△BEG的中线,
∴S△BEG=2S△BEF,
又∵S△DEF=S△CGF,
∴S△BEG=S四边形DEBC,
∴S四边形DEBC=2S△EFB,故③正确.
设∠DEF=x,则∠G=x.
∵FG=FB,∴∠FBG=∠G=x.
∴∠EFB=2x,∠CFB=∠CBF=x.∴∠CFE=∠CFB+∠BFE=x+2x=3x=3∠DEF,故④正确.
12.B 点拨:由题图②可知,BC=CD=4,BD=14-8=6.
如图,连接AC交BD于O,
∴BO=BD=×6=3.
在Rt△BOC中,CO===,
∴AC=2CO=2 ,
∴菱形ABCD的面积=AC·BD=×2 ×6=6 .
当点P在CD上运动时,△ABP的面积不变,为b,
∴b=×6 =3 .
(第12题)
13.C 14.A
二、15.48
16.120°
17.(2+)cm 点拨:过点E作EG⊥BD于点G.
∵BE平分∠DBC,∠EGB=∠BCE=90°,
∴EG=EC=1 cm.
易知△DEG为等腰直角三角形,
∴DE=EG= cm.
∴CD=(1+)cm,
∴BC=(1+)cm.
又∵CF=CE=1 cm,
∴BF=(2+)cm.
18.;
三、19.解:(1)设这个多边形的每个内角是x°,每个外角是y°,
则得到一个方程组
解得
而任何多边形的外角和是360°,
则多边形的边数是360°÷30°=12,
答:这个多边形的边数是12.
(2)设这个多边形的边数为n,
依题意得(n-2)×180°=360°,解得n=9,
答:这个多边形的边数为9.
20.证明:∵四边形ABCD是平行四边形,
∴AD=BC,AD∥BC,∠A=∠C.
∴∠F=∠E.
∵BE=DF,
∴AD+DF=CB+BE,即AF=CE.
在△AGF和△CHE中,
∴△AGF≌△CHE.
∴AG=CH.
21.(1)证明:∵点O为AB的中点,连接DO并延长到点E,使OE=OD,
∴四边形AEBD是平行四边形.
∵AB=AC,AD平分∠BAC,
∴AD⊥BC,∴∠ADB=90°,
∴平行四边形AEBD是矩形.
(2)解:当∠BAC=90°时,
矩形ABCD是正方形.
理由:∵∠BAC=90°,AB=AC,AD平分∠BAC,
∴AD=BD=CD.
∵由(1)得四边形AEBD是矩形,
∴矩形AEBD是正方形.
22.证明:(1)∵四边形ABCD是正方形,
∴AD=AB,∠DAE=∠ABE=90°.
在Rt△DAE与Rt△ABF中,
∴Rt△DAE≌Rt△ABF,
∴BF=AE.
(2)∵Rt△DAE≌Rt△ABF,
∴∠ADE=∠BAF.
∵∠ADE+∠AED=90°,
∴∠BAF+∠AEG=90°,
∴∠AGE=90°,∴AF⊥DE.
23.解:(1)四边形ADCE是菱形.
理由:∵四边形BCED为平行四边形,
∴CE∥BD,CE=BD,BC∥DE.
∵D为AB的中点,∴AD=BD.
∴CE=AD.
∴四边形ADCE为平行四边形.
又∵BC∥DE,
∴∠AFD=∠ACB=90°,
即AC⊥DE.
∴四边形ADCE为菱形.
(2)在Rt△ABC中,
∵∠ACB=90°,AB=16,AC=12,
∴BC=4 .
∵BC=DE,∴DE=4 .
∴四边形ADCE的面积=AC·DE=24 .
(3)当AC=BC时,四边形ADCE为正方形.
证明:∵AC=BC,D为AB的中点,∴CD⊥AB,即∠ADC=90°.
∴菱形ADCE为正方形.
24.解:(1)菱形 (2)矩形
(3)四边形CODP是正方形.
理由:∵四边形ABCD是正方形,
∴AC⊥BD,AC=BD,OA=OC=AC,OB=OD=BD.
∴∠DOC=90°,OD=OC.
∵DP∥OC,OD∥CP,
∴四边形CODP是平行四边形.
∵∠DOC=90°,OD=OC,
∴平行四边形CODP是正方形.
点拨:(1)∵四边形ABCD是矩形,
∴AC=BD,OA=OC=AC,OB=OD=BD,∴OC=OD.
∵DP∥OC,OD∥CP,
∴四边形CODP是平行四边形.
∵OC=OD,
∴平行四边形CODP是菱形.
(2)∵四边形ABCD是菱形,
∴AC⊥BD,∴∠DOC=90°.
∵DP∥OC,OD∥CP,
∴四边形CODP是平行四边形.
∵∠DOC=90°,
∴平行四边形CODP是矩形.
一、选择题(每题2分,共28分)
1.在 ABCD中,∠A+∠C=200°,则∠A的度数为( )
A.130° B.100° C.80° D.70°
2.已知一个多边形的内角和等于900°,则这个多边形是( )
A.五边形 B.六边形 C.七边形 D.八边形
3.如图, ABCD中,对角线AC,BD交于点O,点E是BC的中点.若OE=3 cm,则AB的长为( )
A.12 cm B.9 cm C.6 cm D.3 cm
(第3题) (第4题)
4.如图,点A是直线l外一点,在l上取两点B,C,分别以A,C为圆心,BC,AB长为半径画弧,两弧相交于点D,分别连接AB,AD,CD,则四边形ABCD的( )
A.四条边相等 B.四个角相等
C.对角线互相垂直 D.对角线互相平分
5.如图,已知在菱形ABCD中,对角线AC与BD交于点O,∠BAD=120°,AC=4,则该菱形的面积是( )
(第5题)
A.16 B.16 C.8 D.8
6.如图,把一张长方形纸片对折两次,然后剪下一个角,为了得到一个钝角为100°的菱形,裁剪线与第二条折痕所成的夹角度数为( )
(第6题)
A.25°或50° B.20°或50°
C.40°或50° D.40°或80°
7.如图,在矩形ABCD中,AD=3AB,点G,H分别在AD,BC上,连接BG,DH,且BG∥DH,若四边形BHDG为菱形,则=( )
(第7题)
A. B. C. D.
8.科技馆为某机器人编制了一个程序,如果机器人在平地上按照图中所示的步骤行走,那么该机器人所走的总路程为( )
A.12米 B.16米 C.18米 D.20米
(第8题) (第9题)
9.如图,在△ABC中,点D,E分别是边AB,AC的中点,点F是线段DE上的一点.连接AF,BF,∠AFB=90°,且AB=8,BC=14,则EF的长是( )
A.2 B.3 C.4 D.5
10.如图,在矩形ABCD中,对角线AC、BD交于点O,∠BAD的平分线交BC于E,若∠EAC=15°,则∠COE=( )
A.45° B.60° C.75° D.30°
(第10题) (第11题)
11.如图,在 ABCD中,CD=2AD,BE⊥AD于点E,F为DC的中点,连接EF,BF,给出下列结论:①∠ABC=2∠ABF;②EF=BF;③S四边形DEBC=2S△EFB;④∠CFE=3∠DEF.其中正确的结论有( )
A.1个 B.2个 C.3个 D.4个
12.如图①,在菱形ABCD中,动点P从点B出发,沿△BCD的边运动.设点P经过的路程为x,△ABP的面积为y.把y看成x的函数,函数的图像如图②所示,则图②中的b等于( )
(第12题)
A.8 B.3 C.5 D.4
13.如图,在Rt△ABC中,∠A=90°,P为边BC上一动点,PE⊥AB于E,PF⊥AC于F,动点P从点B出发,沿着BC匀速向终点C运动,则线段EF的值大小变化情况是( )
A.一直增大 B.一直减小
C.先减小后增大 D.先增大后减小
(第13题) (第14题)
14.如图,已知△ABC的周长为1,连接△ABC三边的中点构成第二个三角形,再连接第二个三角形三边中点构成第三个三角形,依此类推,则第2 022个三角形的周长是( )
A. B. C. D.
二、填空题(共4小题,每题3分,共12分)
15.如图,四边形ABCD是菱形,点O是两条对角线的交点,过点O的三条直线将菱形分成阴影和空白部分,当菱形的两条对角线长分别为12和16时,则阴影部分面积为________.
(第15题) (第16题)
16.如图,在四边形ABCD中,点P是对角线BD的中点,点E、F分别是AB、CD的中点,AD=BC,∠PEF=30°,则∠EPF的度数是________.
17.如图,BD为正方形ABCD的对角线,BE平分∠DBC,交DC于点E,延长BC到F,使CF=CE,连接DF.若CE=1 cm,则BF=________.
(第17题)
18.菱形OBCD在平面直角坐标系中的位置如图所示,顶点B(2,0),∠DOB=60°,点P是对角线OC上一个动点,E,则EP+BP的最小值为________,此时点P的坐标为________.
(第18题)
三、解答题(19~22题每题9分,23、24题每题12分,共60分)
19.(1)已知一个正多边形的每个内角比它的每个外角的4倍多30°,求这个多边形的边数;
(2)一个多边形的外角和是内角和的,求这个多边形的边数.
20.如图,在 ABCD中,点E,F分别在边CB,AD的延长线上,且BE=DF,连接EF,分别与AB,CD交于点G,H.
求证:AG=CH.
(第20题)
21.如图,△ABC中,AB=AC,AD平分∠BAC,点O为AB的中点,连接DO并延长到点E,使OE=OD,连接AE,BE.
(1)求证:四边形AEBD是矩形;
(2)当△ABC满足什么条件时,矩形AEBD是正方形,并说明理由.
(第21题)
22.如图,正方形ABCD中,E,F分别是AB,BC边上的点,AF与DE相交于点G,且AF=DE.求证:
(1)BF=AE;
(2)AF⊥DE.
(第22题)
23.如图,△ABC中,∠ACB=90°,D为AB的中点,四边形BCED为平行四边形,DE,AC相交于F.连接DC,AE.
(1)试确定四边形ADCE的形状,并说明理由;
(2)若AB=16,AC=12,求四边形ADCE的面积;
(3)当△ABC满足什么条件时,四边形ADCE为正方形?请给予证明.
(第23题)
24.(1)如图①,矩形ABCD的对角线AC、BD交于点O,过点C作BD的平行线,过点D作AC的平行线,两线交于点P,则四边形CODP的形状是________;
(2)如图②,若(1)中的矩形变为菱形,其他条件不变,则四边形CODP的形状是________;
(3)如图③,若(1)中的矩形变为正方形,其他条件不变,请判断四边形CODP的形状,并说明理由.
(第24题)
答案
一、1.B 2.C 3.C 4.D 5.C 6.C
7.C 点拨:设AB=1,则AD=3.若四边形BHDG为菱形,则BG=GD.设BG=GD=x,则AG=3-x.在Rt△ABG中,12+=x2 ,解得x= ,所以==.
8.C 9.B 10.A
11.D 点拨:∵在 ABCD中,CD=2AD,F为DC的中点,∴CF=CD=AD=BC,∴∠CBF=∠CFB.
∵AB∥CD,∴∠CFB=∠ABF.
∴∠CBF=∠ABF.∴∠ABC=∠ABF+∠CBF=2∠ABF.故①正确.
如图,延长EF,BC,相交于点G.
(第11题)
易证得△DEF≌△CGF,∴FE=FG.
∵BE⊥AD,AD∥BC,∴∠EBG=90°.
根据直角三角形斜边上的中线等于斜边的一半得,EF=BF,故②正确.
∵BF是△BEG的中线,
∴S△BEG=2S△BEF,
又∵S△DEF=S△CGF,
∴S△BEG=S四边形DEBC,
∴S四边形DEBC=2S△EFB,故③正确.
设∠DEF=x,则∠G=x.
∵FG=FB,∴∠FBG=∠G=x.
∴∠EFB=2x,∠CFB=∠CBF=x.∴∠CFE=∠CFB+∠BFE=x+2x=3x=3∠DEF,故④正确.
12.B 点拨:由题图②可知,BC=CD=4,BD=14-8=6.
如图,连接AC交BD于O,
∴BO=BD=×6=3.
在Rt△BOC中,CO===,
∴AC=2CO=2 ,
∴菱形ABCD的面积=AC·BD=×2 ×6=6 .
当点P在CD上运动时,△ABP的面积不变,为b,
∴b=×6 =3 .
(第12题)
13.C 14.A
二、15.48
16.120°
17.(2+)cm 点拨:过点E作EG⊥BD于点G.
∵BE平分∠DBC,∠EGB=∠BCE=90°,
∴EG=EC=1 cm.
易知△DEG为等腰直角三角形,
∴DE=EG= cm.
∴CD=(1+)cm,
∴BC=(1+)cm.
又∵CF=CE=1 cm,
∴BF=(2+)cm.
18.;
三、19.解:(1)设这个多边形的每个内角是x°,每个外角是y°,
则得到一个方程组
解得
而任何多边形的外角和是360°,
则多边形的边数是360°÷30°=12,
答:这个多边形的边数是12.
(2)设这个多边形的边数为n,
依题意得(n-2)×180°=360°,解得n=9,
答:这个多边形的边数为9.
20.证明:∵四边形ABCD是平行四边形,
∴AD=BC,AD∥BC,∠A=∠C.
∴∠F=∠E.
∵BE=DF,
∴AD+DF=CB+BE,即AF=CE.
在△AGF和△CHE中,
∴△AGF≌△CHE.
∴AG=CH.
21.(1)证明:∵点O为AB的中点,连接DO并延长到点E,使OE=OD,
∴四边形AEBD是平行四边形.
∵AB=AC,AD平分∠BAC,
∴AD⊥BC,∴∠ADB=90°,
∴平行四边形AEBD是矩形.
(2)解:当∠BAC=90°时,
矩形ABCD是正方形.
理由:∵∠BAC=90°,AB=AC,AD平分∠BAC,
∴AD=BD=CD.
∵由(1)得四边形AEBD是矩形,
∴矩形AEBD是正方形.
22.证明:(1)∵四边形ABCD是正方形,
∴AD=AB,∠DAE=∠ABE=90°.
在Rt△DAE与Rt△ABF中,
∴Rt△DAE≌Rt△ABF,
∴BF=AE.
(2)∵Rt△DAE≌Rt△ABF,
∴∠ADE=∠BAF.
∵∠ADE+∠AED=90°,
∴∠BAF+∠AEG=90°,
∴∠AGE=90°,∴AF⊥DE.
23.解:(1)四边形ADCE是菱形.
理由:∵四边形BCED为平行四边形,
∴CE∥BD,CE=BD,BC∥DE.
∵D为AB的中点,∴AD=BD.
∴CE=AD.
∴四边形ADCE为平行四边形.
又∵BC∥DE,
∴∠AFD=∠ACB=90°,
即AC⊥DE.
∴四边形ADCE为菱形.
(2)在Rt△ABC中,
∵∠ACB=90°,AB=16,AC=12,
∴BC=4 .
∵BC=DE,∴DE=4 .
∴四边形ADCE的面积=AC·DE=24 .
(3)当AC=BC时,四边形ADCE为正方形.
证明:∵AC=BC,D为AB的中点,∴CD⊥AB,即∠ADC=90°.
∴菱形ADCE为正方形.
24.解:(1)菱形 (2)矩形
(3)四边形CODP是正方形.
理由:∵四边形ABCD是正方形,
∴AC⊥BD,AC=BD,OA=OC=AC,OB=OD=BD.
∴∠DOC=90°,OD=OC.
∵DP∥OC,OD∥CP,
∴四边形CODP是平行四边形.
∵∠DOC=90°,OD=OC,
∴平行四边形CODP是正方形.
点拨:(1)∵四边形ABCD是矩形,
∴AC=BD,OA=OC=AC,OB=OD=BD,∴OC=OD.
∵DP∥OC,OD∥CP,
∴四边形CODP是平行四边形.
∵OC=OD,
∴平行四边形CODP是菱形.
(2)∵四边形ABCD是菱形,
∴AC⊥BD,∴∠DOC=90°.
∵DP∥OC,OD∥CP,
∴四边形CODP是平行四边形.
∵∠DOC=90°,
∴平行四边形CODP是矩形.
同课章节目录
- 第十八章 数据的收集与整理
- 18.1 统计的初步认识
- 18.2 抽样调查
- 18.3 数据的整理与表示
- 18.4 频数分布表与直方图
- 第十九章 平面直角坐标系
- 19.1 确定平面上物体的位置
- 19.2 平面直角坐标系
- 19.3 坐标与图形的位置
- 19.4 坐标与图形的变化
- 第二十章 函数
- 20.1 常量和变量
- 20.2 函数
- 20.3 函数的表示
- 20.4 函数的初步应用
- 第二十一章 一次函数
- 21.1 一次函数
- 21.2 一次函数的图像和性质
- 21.3 用待定系数法确定一次函数表达式
- 21.4 一次函数的应用
- 21.5 一次函数与二元一次方程的关系
- 第二十二章 四边形
- 22.1 平行四边形的性质
- 22.2 平行四边形的判断
- 22.3 三角形的中位线
- 22.4 矩形
- 22.5 菱形
- 22.6 正方形
- 22.7 多边形的内角和与外角和
