2021-2022学年沪科版数学九年级上册22.1.3 比例的性质3 课件(共19张PPT)
文档属性
| 名称 | 2021-2022学年沪科版数学九年级上册22.1.3 比例的性质3 课件(共19张PPT) |  | |
| 格式 | zip | ||
| 文件大小 | 599.9KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 沪科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-10-20 09:36:17 | ||
图片预览




文档简介
(共19张PPT)
22.1.3 比例的性质(3)
例:如图,已知线段AB长度为a,点P是AB上一点,
且使AB:AP=AP:PB.求线段AP的长和的值.
新知讲解
A
B
P
例:如图,已知线段AB长度为a,点P是AB上一点,
且使AB:AP=AP:PB.求线段AP的长和的值.
解:设AP=x,那么PB=a-x,根据题意,得
a:x=x:(a-x)
解方程得:
因为线段长度不能是负值,所以取x=
即AP=
于是
新知讲解
A
B
P
把一条线段分成两部分,使其中较长线段为全线段与较短线段的比例中项,这样的线段分割叫黄金分割。分割点叫做这条线段的黄金分割点;比值 叫黄金数
B
P
A
如图,点P将线段AB分成两条线段AP与BP,
如果AB:AP=AP:BP,则线段AB被点P黄金分割.
点P称为线段AB的黄金分割点.
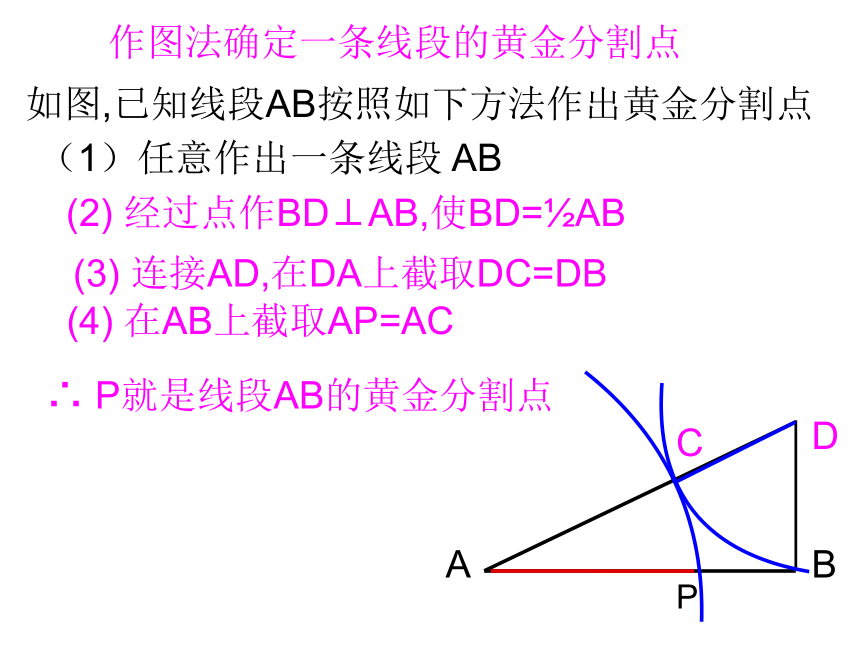
作图法确定一条线段的黄金分割点
如图,已知线段AB按照如下方法作出黄金分割点
(1)任意作出一条线段 AB
(2) 经过点作BD⊥AB,使BD= AB
(3) 连接AD,在DA上截取DC=DB
(4) 在AB上截取AP=AC
∴ P就是线段AB的黄金分割点
A
B
D
C
P
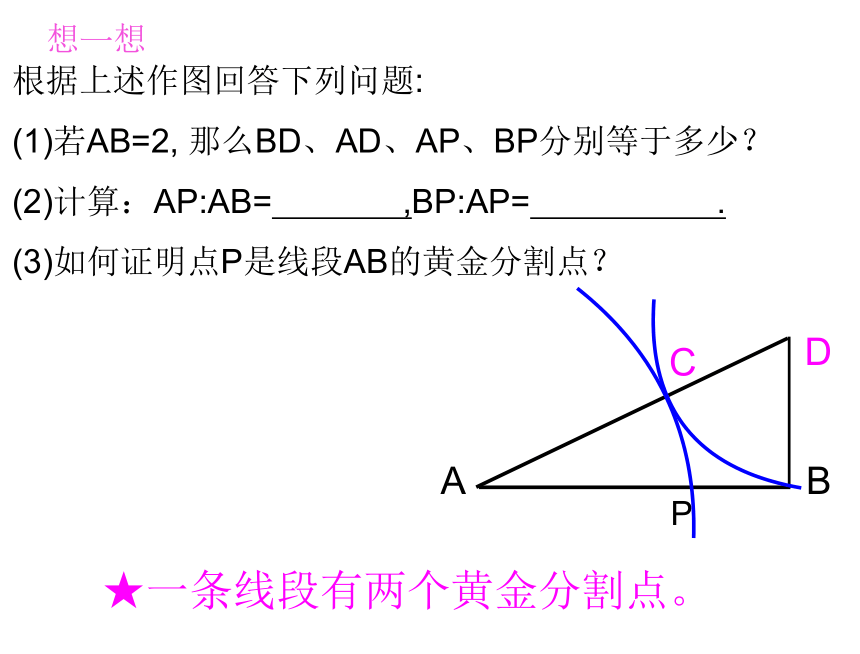
根据上述作图回答下列问题:
(1)若AB=2, 那么BD、AD、AP、BP分别等于多少?
(2)计算:AP:AB= ,BP:AP= .
(3)如何证明点P是线段AB的黄金分割点?
想一想
★一条线段有两个黄金分割点。
C
D
A
B
P
F
C
A
E
B
D
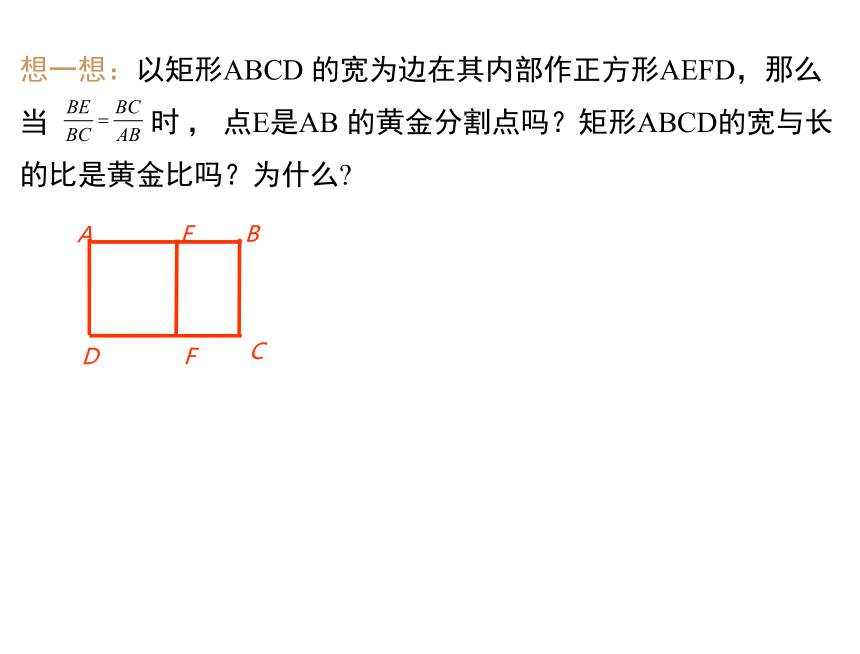
想一想:以矩形ABCD 的宽为边在其内部作正方形AEFD,那么当 时 , 点E是AB 的黄金分割点吗?矩形ABCD的宽与长的比是黄金比吗?为什么
点E是AB的黄金分割点
(即 )是黄金比
矩形ABCD的宽与长的比是黄金比
宽与长的比等于黄金比的矩形也称为黄金矩形.
A
B
C
D
E
F
上海东方明珠电视塔高468m,上球体是塔身的黄金分割点,它到塔底部的距离大约是多少米(精确到0.1m)
468m
实际应用
468×0.618≈289.2m
数学美的魅力
古埃及胡夫金字塔
文明古国埃及的金字塔,形似方锥,大小各异。但这些金字塔底面的边
长与高这比都接近于0.618.
据有关测定, 当气温处于人体正常体温的黄金比值时 , 人体感到最舒适。因此夏天使用空调时室内温度调到什么温度最适合 (人的正常体温36.2℃~ 37.2℃)
22.4℃~ 23.0℃
当植物的枝干的夹角137°28′时,通风和采光能达到最好效果, 你知道这是为什么吗
≈0.618
勾股定理和黄金分割是几何中的双宝,
“前者好似黄金,后者堪称珠玉”。
黄金分割的魅力远不止……
例:在人体躯干与身高的比例上,肚脐是理想的黄金分割点,即比值越接近0.618越给人以美感.小明的妈妈脚底到肚脐的长度与身高的比为0.60,她的身高为1.60m,她应该穿多高的高跟鞋看起来会更美?
解:设肚脐到脚底的距离为 x m,根据题意,得
,解得x = 0.96.
设穿上 y m高的高跟鞋看起来会更美,则
解得 y≈0.075,而0.075m=7.5cm.
故她应该穿约为7.5cm高的高跟鞋看起来会更美.
1.在中华经典美文阅读中,小明同学发现自己的一本书的宽与长之比为黄金比,已知这本书的长为20 cm,则它的宽约为( )
(A)12.36 cm (B)13.6 cm (C)32.36 cm (D)7.64 cm
A
随堂练习
2.如图是一种贝壳的俯视图,点C分线段AB近似于黄金分割,已知AB=10 cm,则AC的长约为_____cm.(结果精确到0.1 cm)
6.2
3.已知线段AB,点P是它的黄金分割点,AP>BP,设以AP为边的正方形的面积为S1,以PB、AB为边的矩形面积为S2,则S1与S2的关系是( )
A.S1>S2 B.S1P
A
B
C
4.点C是线段AB的黄金分割点,如果AB=4,求线段 AC的长度.
5、如图,乐器上的一根弦AB=80cm两个端点A、B固定在乐器板面上,支撑点C是靠近点B的黄金分割点(即AC是AB与BC的比例中项),支撑点D是靠近点A的黄金分割点,求AC、DC、BC的长。
6.如图,设AB是已知线段,在AB上作正方形ABCD;取AD的中点E,连接EB;延长DA至F,使EF=EB;以线段AF为边作正方形AFGH.则点H就是AB的黄金分割点.为什么?
解: 设AB=1,那么在 Rt△BAE 中,
A
B
C
D
E
F
G
H
比例线段
如果那么 ad = bc
基本
性质
等比
性质
如果ad = bc(a , b, c, d)都不等于0,那么
如果
课堂总结
黄金
分割
点C把线段AB分成两条线段AC和BC,如果 ,
那么称线段AB被点C黄金分割.点C叫做线段AB的
黄金分割点,AC与AB的比称为黄金比.
定义
一条线段有两个黄金分割点
黄金比:较长线段:原线段 =
22.1.3 比例的性质(3)
例:如图,已知线段AB长度为a,点P是AB上一点,
且使AB:AP=AP:PB.求线段AP的长和的值.
新知讲解
A
B
P
例:如图,已知线段AB长度为a,点P是AB上一点,
且使AB:AP=AP:PB.求线段AP的长和的值.
解:设AP=x,那么PB=a-x,根据题意,得
a:x=x:(a-x)
解方程得:
因为线段长度不能是负值,所以取x=
即AP=
于是
新知讲解
A
B
P
把一条线段分成两部分,使其中较长线段为全线段与较短线段的比例中项,这样的线段分割叫黄金分割。分割点叫做这条线段的黄金分割点;比值 叫黄金数
B
P
A
如图,点P将线段AB分成两条线段AP与BP,
如果AB:AP=AP:BP,则线段AB被点P黄金分割.
点P称为线段AB的黄金分割点.
作图法确定一条线段的黄金分割点
如图,已知线段AB按照如下方法作出黄金分割点
(1)任意作出一条线段 AB
(2) 经过点作BD⊥AB,使BD= AB
(3) 连接AD,在DA上截取DC=DB
(4) 在AB上截取AP=AC
∴ P就是线段AB的黄金分割点
A
B
D
C
P
根据上述作图回答下列问题:
(1)若AB=2, 那么BD、AD、AP、BP分别等于多少?
(2)计算:AP:AB= ,BP:AP= .
(3)如何证明点P是线段AB的黄金分割点?
想一想
★一条线段有两个黄金分割点。
C
D
A
B
P
F
C
A
E
B
D
想一想:以矩形ABCD 的宽为边在其内部作正方形AEFD,那么当 时 , 点E是AB 的黄金分割点吗?矩形ABCD的宽与长的比是黄金比吗?为什么
点E是AB的黄金分割点
(即 )是黄金比
矩形ABCD的宽与长的比是黄金比
宽与长的比等于黄金比的矩形也称为黄金矩形.
A
B
C
D
E
F
上海东方明珠电视塔高468m,上球体是塔身的黄金分割点,它到塔底部的距离大约是多少米(精确到0.1m)
468m
实际应用
468×0.618≈289.2m
数学美的魅力
古埃及胡夫金字塔
文明古国埃及的金字塔,形似方锥,大小各异。但这些金字塔底面的边
长与高这比都接近于0.618.
据有关测定, 当气温处于人体正常体温的黄金比值时 , 人体感到最舒适。因此夏天使用空调时室内温度调到什么温度最适合 (人的正常体温36.2℃~ 37.2℃)
22.4℃~ 23.0℃
当植物的枝干的夹角137°28′时,通风和采光能达到最好效果, 你知道这是为什么吗
≈0.618
勾股定理和黄金分割是几何中的双宝,
“前者好似黄金,后者堪称珠玉”。
黄金分割的魅力远不止……
例:在人体躯干与身高的比例上,肚脐是理想的黄金分割点,即比值越接近0.618越给人以美感.小明的妈妈脚底到肚脐的长度与身高的比为0.60,她的身高为1.60m,她应该穿多高的高跟鞋看起来会更美?
解:设肚脐到脚底的距离为 x m,根据题意,得
,解得x = 0.96.
设穿上 y m高的高跟鞋看起来会更美,则
解得 y≈0.075,而0.075m=7.5cm.
故她应该穿约为7.5cm高的高跟鞋看起来会更美.
1.在中华经典美文阅读中,小明同学发现自己的一本书的宽与长之比为黄金比,已知这本书的长为20 cm,则它的宽约为( )
(A)12.36 cm (B)13.6 cm (C)32.36 cm (D)7.64 cm
A
随堂练习
2.如图是一种贝壳的俯视图,点C分线段AB近似于黄金分割,已知AB=10 cm,则AC的长约为_____cm.(结果精确到0.1 cm)
6.2
3.已知线段AB,点P是它的黄金分割点,AP>BP,设以AP为边的正方形的面积为S1,以PB、AB为边的矩形面积为S2,则S1与S2的关系是( )
A.S1>S2 B.S1
A
B
C
4.点C是线段AB的黄金分割点,如果AB=4,求线段 AC的长度.
5、如图,乐器上的一根弦AB=80cm两个端点A、B固定在乐器板面上,支撑点C是靠近点B的黄金分割点(即AC是AB与BC的比例中项),支撑点D是靠近点A的黄金分割点,求AC、DC、BC的长。
6.如图,设AB是已知线段,在AB上作正方形ABCD;取AD的中点E,连接EB;延长DA至F,使EF=EB;以线段AF为边作正方形AFGH.则点H就是AB的黄金分割点.为什么?
解: 设AB=1,那么在 Rt△BAE 中,
A
B
C
D
E
F
G
H
比例线段
如果那么 ad = bc
基本
性质
等比
性质
如果ad = bc(a , b, c, d)都不等于0,那么
如果
课堂总结
黄金
分割
点C把线段AB分成两条线段AC和BC,如果 ,
那么称线段AB被点C黄金分割.点C叫做线段AB的
黄金分割点,AC与AB的比称为黄金比.
定义
一条线段有两个黄金分割点
黄金比:较长线段:原线段 =
