2021-2022学年人教版七年级数学上册 1.5.1有理数的乘方 课件(共17张PPT)
文档属性
| 名称 | 2021-2022学年人教版七年级数学上册 1.5.1有理数的乘方 课件(共17张PPT) | 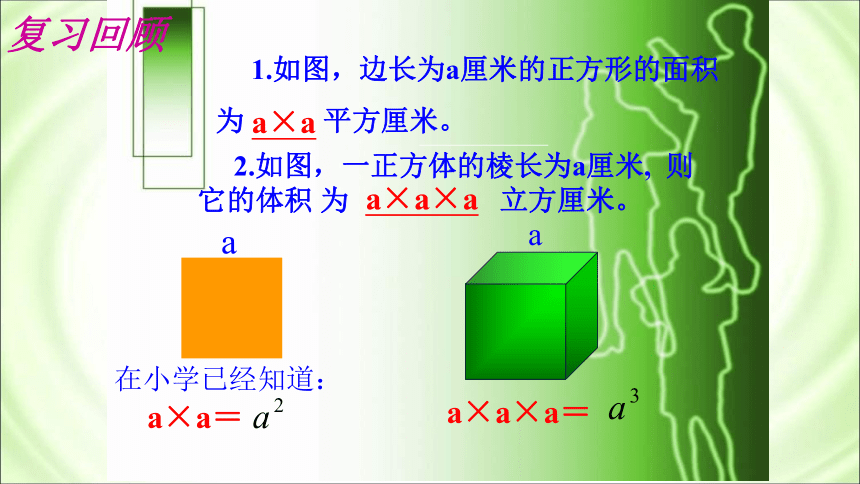 | |
| 格式 | zip | ||
| 文件大小 | 751.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-10-20 09:53:15 | ||
图片预览







文档简介
(共17张PPT)
2.如图,一正方体的棱长为a厘米, 则它的体积 为 立方厘米。
a×a×a
复习回顾
1.如图,边长为a厘米的正方形的面积
为 平方厘米。
a×a
a
a
在小学已经知道:
a×a=
a×a×a=
2.11 有理数的乘方
国际象棋为一正方形盘,盘面有纵横各8格、共64个方格。
探究新知
棋盘上的数学
古印度人西塔发明了国际象棋,献给了国王,国王十分高兴,决定重赏西塔。西塔说:“陛下,就在这个棋盘上放一些麦粒吧!第1格放1粒,第2格放2粒,第3格放4粒,然后是8粒、16粒、32粒…,一直到第64格。”“你真傻!就要这么一点麦粒?!”国王哈哈大笑。西塔说:“就怕您的国库里没有这么多小麦!”
第1格: 1
第2格: 2
第3格: 4
=2×2
第4格: 8
第5格: 16
……
第64格
=2 ×2 ×2
= 2 ×2 ×2 ×2
63个2
=2×2×······×2
聪明的同学们,你能猜想出第64格的小麦粒是多少粒吗
请比较第五格的麦粒个数2×2×2×2和第七格的麦粒个数2×2×2×2×2×2.
1.这两个式子有什么相同点
2.想一想:这样的运算能像平方、立方那样简写吗?
an
幂
底数
指数
定义:求几个相同因数的积的运算,叫做乘方。乘方的结果叫做幂。
a叫做底数,n叫做指数、an读作a的n次幂或a的n次方
填一填
运算 加法 减法 乘法 除法 乘方
结果
即:乘方是一种运算,这种运算的结果叫做幂。
和
差
积
商
幂
把下列乘法式子写成乘方的形式:
1.1×1×1×1×1×1×1= ;
2.2.1×2.1= ;
3.(-3)(-3)(-3)(-3)= ;
4. = ;
注意:
当底数是负数或分数时,写成乘方形式时,必须加上括号。
学以致用
1.在 中,其中12叫__,10叫做__,
读作: _ ___,
2..在 中,底数是__,指数是__,
读作:_ ___
3).如果 数字5 看作幂,底数是 ,指数 。读作:
5
1
5的1次幂
究竟有多少粒?
这些麦子究竟有多少 若以每立方米仓库约可存放150万粒麦子计算,这些麦子的体积大约是120000亿立方米。假如造一个高4米、宽10米的仓库存放这些麦子,那么仓库的长度大约是3亿千米,大致是地球到太阳的距离的2倍,或绕地球赤道转7500圈,而要生产这么多麦子,全世界需要数千年,虽然国度十分富有,但要这么多的麦子,国王是怎么也拿不出来的.
拓展延伸
和
和
在表示的意义、读法及运算结果有什么区别?
计算:
= 2×2=4
= 2×2×2=8
= 2×2×2×2=16
= 2×2×2×2×2=32
= (-2)(-2) = 4
= (-2)(-2)(-2) = -8
= (-2)(-2)(-2)(-2)= 16
= (-2)(-2)(-2)(-2)(-2) = -32
正数的任何次幂都是_____.
乘方运算的法则:
负数的奇次幂是_____;
负数的偶次幂是____.
探究新知
负数的偶次幂是正数
正数的任何次幂都是正数
负数的奇次幂是负数
零的任何正整数次幂都零
发现规律
学以致用
=1000
=100000
=-1
=1
=-0.001
乘方、幂、底数和指数的定义
an
幂
指数
底数
2. 有理数乘方法则
正数的任何次幂都是正数
负数的奇次幂是负数,负数的偶次幂是正数
本节课里我的收获是……
课后作业:
1.仔细阅读教材59页的材料,感悟乘方的奥妙.
2.熟记1至20的平方和1至10的立方.
3.A层:《课本》P58第2、4题;P78第19题(不抄题).(约15分钟)
B层:《课本》P48例3.
2.如图,一正方体的棱长为a厘米, 则它的体积 为 立方厘米。
a×a×a
复习回顾
1.如图,边长为a厘米的正方形的面积
为 平方厘米。
a×a
a
a
在小学已经知道:
a×a=
a×a×a=
2.11 有理数的乘方
国际象棋为一正方形盘,盘面有纵横各8格、共64个方格。
探究新知
棋盘上的数学
古印度人西塔发明了国际象棋,献给了国王,国王十分高兴,决定重赏西塔。西塔说:“陛下,就在这个棋盘上放一些麦粒吧!第1格放1粒,第2格放2粒,第3格放4粒,然后是8粒、16粒、32粒…,一直到第64格。”“你真傻!就要这么一点麦粒?!”国王哈哈大笑。西塔说:“就怕您的国库里没有这么多小麦!”
第1格: 1
第2格: 2
第3格: 4
=2×2
第4格: 8
第5格: 16
……
第64格
=2 ×2 ×2
= 2 ×2 ×2 ×2
63个2
=2×2×······×2
聪明的同学们,你能猜想出第64格的小麦粒是多少粒吗
请比较第五格的麦粒个数2×2×2×2和第七格的麦粒个数2×2×2×2×2×2.
1.这两个式子有什么相同点
2.想一想:这样的运算能像平方、立方那样简写吗?
an
幂
底数
指数
定义:求几个相同因数的积的运算,叫做乘方。乘方的结果叫做幂。
a叫做底数,n叫做指数、an读作a的n次幂或a的n次方
填一填
运算 加法 减法 乘法 除法 乘方
结果
即:乘方是一种运算,这种运算的结果叫做幂。
和
差
积
商
幂
把下列乘法式子写成乘方的形式:
1.1×1×1×1×1×1×1= ;
2.2.1×2.1= ;
3.(-3)(-3)(-3)(-3)= ;
4. = ;
注意:
当底数是负数或分数时,写成乘方形式时,必须加上括号。
学以致用
1.在 中,其中12叫__,10叫做__,
读作: _ ___,
2..在 中,底数是__,指数是__,
读作:_ ___
3).如果 数字5 看作幂,底数是 ,指数 。读作:
5
1
5的1次幂
究竟有多少粒?
这些麦子究竟有多少 若以每立方米仓库约可存放150万粒麦子计算,这些麦子的体积大约是120000亿立方米。假如造一个高4米、宽10米的仓库存放这些麦子,那么仓库的长度大约是3亿千米,大致是地球到太阳的距离的2倍,或绕地球赤道转7500圈,而要生产这么多麦子,全世界需要数千年,虽然国度十分富有,但要这么多的麦子,国王是怎么也拿不出来的.
拓展延伸
和
和
在表示的意义、读法及运算结果有什么区别?
计算:
= 2×2=4
= 2×2×2=8
= 2×2×2×2=16
= 2×2×2×2×2=32
= (-2)(-2) = 4
= (-2)(-2)(-2) = -8
= (-2)(-2)(-2)(-2)= 16
= (-2)(-2)(-2)(-2)(-2) = -32
正数的任何次幂都是_____.
乘方运算的法则:
负数的奇次幂是_____;
负数的偶次幂是____.
探究新知
负数的偶次幂是正数
正数的任何次幂都是正数
负数的奇次幂是负数
零的任何正整数次幂都零
发现规律
学以致用
=1000
=100000
=-1
=1
=-0.001
乘方、幂、底数和指数的定义
an
幂
指数
底数
2. 有理数乘方法则
正数的任何次幂都是正数
负数的奇次幂是负数,负数的偶次幂是正数
本节课里我的收获是……
课后作业:
1.仔细阅读教材59页的材料,感悟乘方的奥妙.
2.熟记1至20的平方和1至10的立方.
3.A层:《课本》P58第2、4题;P78第19题(不抄题).(约15分钟)
B层:《课本》P48例3.
