苏科版八年级数学上册 第一章 小结与思考(课件)(共20张PPT)
文档属性
| 名称 | 苏科版八年级数学上册 第一章 小结与思考(课件)(共20张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 218.1KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 苏科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-10-20 09:58:08 | ||
图片预览







文档简介
(共20张PPT)
小结与思考
知识归纳
1.由不在同一条直线上的三条 首尾依次相接所
组成的图形叫做三角形.
线段
2.三角形的分类:
按角可分为 ;
锐角三角形、直角三角形、钝角三角形
不等边三角形
等腰三角形
等边三角形
底和腰不等的等腰三角形
按边可分为
1. 若一个三角形三个内角度数的比为2:3:4,那么
这个三角形是( )
A.直角三角形 B.锐角三角形
C.钝角三角形 D.等边三角形
【基础训练】
B
40°60°80°
知识归纳
3.三角形 大于第三边,
小于第三边.
任意两边之和
任意两边之差
【基础训练】
如果三角形的两边长分别为3和5,第三边长是偶数
则第三边长可以是( )
A.2 B.3 C.4 D.8
C
两边之差<第三边<两边之和
2<第三边<8
4和6
4.三角形具有 性.
知识归纳
稳定
5.三角形的内角和等于 ;外角和等于 .
180°
360°
6.三角形的外角等于 的和,
三角形的外角大于任何一个 的内角.
与它不相邻的两个内角
与它不相邻
【基础训练】
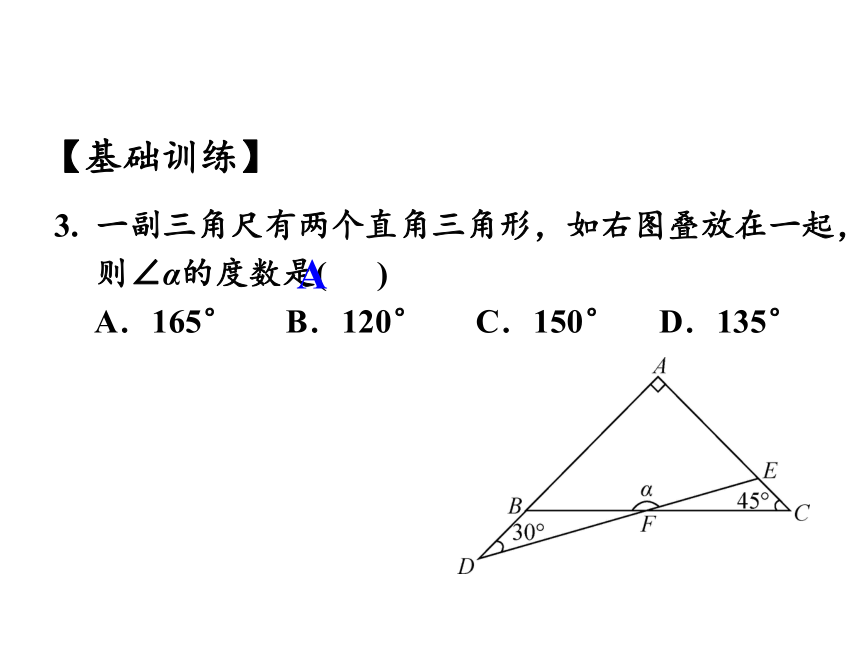
3. 一副三角尺有两个直角三角形,如右图叠放在一起,
则∠α的度数是( )
A.165° B.120° C.150° D.135°
A
知识归纳
7.三角形中的有关线段:
(1)三角形的高;三角形的中线;三角形的角平分线;
(2)三角形的中位线:连结三角形两边 的线段.
三角形的中位线 于第三边,并且等于 .
中点
平行
第三边的一半
【基础训练】
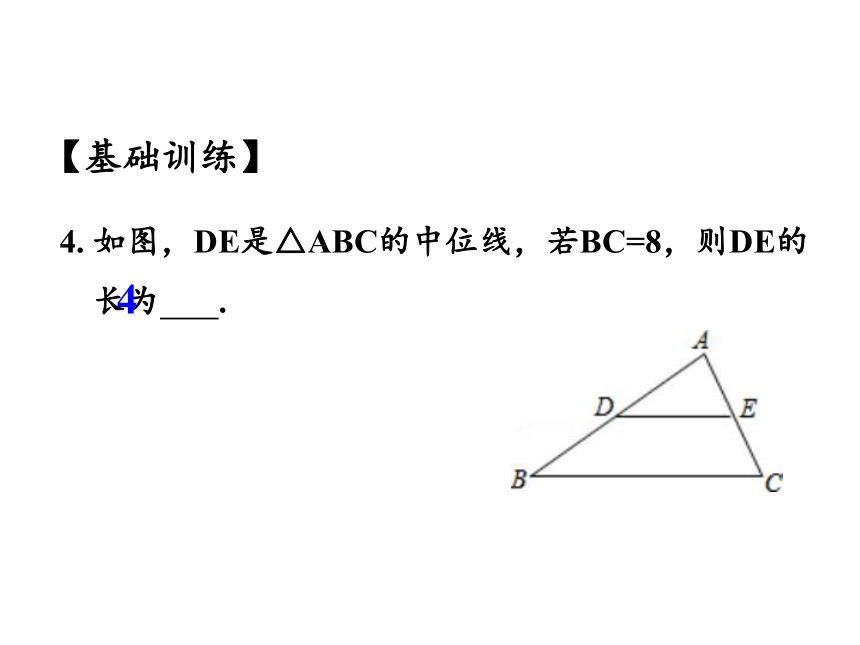
4. 如图,DE是△ABC的中位线,若BC=8,则DE的
长为 .
4
知识归纳
8.(1)线段垂直平分线上的点到 的距离相等;
(2)到 距离相等的点在这条线段的垂直平
分线上.
线段两端点
线段两端点
100°
【基础训练】
5. 如图,线段AC的垂直平分线交线段AB于点D,
∠A=50°,则∠BDC= .
知识归纳
9.(1)角平分线上的点到 的距离相等;
(2)角的内部到 距离相等的点在这个角的角
平分线上.
角两边
角两边
12
【基础训练】
6. 如图,直角△ABC中,∠C=90°,BD是角平分线,
CD=3,AB=8,则△ABD的面积是 .
E
8
3
3
知识归纳
10.能够完全 的两个三角形叫做全等三角形.
重合
① ② ④
下列说法:①用一张底片冲洗出来的10张1寸相片是全等
形;②我国国旗上的4颗小五角星是全等形; ③所有的
正方形是全等形;④全等形的面积一定相等.
其中正确的是 (填序号)
【基础训练】
√
√
√
知识归纳
11.全等三角形的性质:全等三角形的对应边 ,
对应角 ,对应边上的高 ,对应边上的中
线 ,对应的角平分线 ;全等三角形的
面积 ,周长 .
相等
相等
相等
相等
相等
相等
相等
30°
【基础训练】
8. 如图,△ACB≌△A′CB′,∠ACA′=30°,则
∠BCB′的度数为 .
知识归纳
12.全等三角形的判定方法:
(1)所有三角形都可用的有 ;
(2)直角三角形特有的是 .
SAS、
ASA、AAS、
SSS
HL
DE=AB
【基础训练】
9. 如图,AB∥ED,CD=BF,若△ABC≌△EDF,则还
需要补充的条件可以是 .
答案不唯一
典型例题
例1. (1)如图,点O在△ABC内,且到三边的距离相等.
若∠BOC=120°,则tanA的值为 .
∠BOC=90°+ ∠A
∠BOC=90° ∠A
∠D= ∠A
例1. (2)如图,在Rt△ABC中,∠C=90°,∠CAB的平
分线交BC于D,DE是AB的垂直平分线,垂足
为E.若BC=3,则DE的长为 .
1
例1. (3)如图.三角形纸片ABC中,∠A=65°,∠B=75°
将纸片的一角折叠,使点C落在△ABC内,若
∠1=20°,则∠2的度数为 .
60°
例1. (4)如图,四边形ABCD中,∠BAD=∠BCD=90°,
AB=AD,若四边形ABCD的面积是24cm2,则
AC的长是 cm.
例2. (1)作图发现:如图1, 已知△ABC, 小涵同学以AB , AC
为边向△ABC外作等边△ABD和等△ACE.连接BE, CD.
这时他发现BE与CD的数量关系是 .
(2)拓展探究:如图2, 已知△ABC,小涵同学以AB, AC为边向
外作正方形ABFD和正方形ACGE,连接BE, CD,试判断BE
与CD之间的数量关系,并说明理由.
(3)解决问题:如图3, 要测量池塘两岸相对的两点B, E的距
离已经测得∠ABC=45°, ∠CAE=90°, AB=BC =200米,
AC=AE, 求BE长.
BE=CD
例3. 如图, △ABC中, ∠BAC=90°, AB=AC, AD⊥BC, 垂
足是D, AE平分∠BAD, 交BC于点E. 在△ABC外有一点F
使FA⊥AE, FC⊥BC.
(1)求证:BE=CF;
(2)在AB上取一点M, 使BM=2DE, 连接MC, 交AD于点N,
连接ME. 求证:
①ME⊥BC; ②CM平分∠ACE; ③DE=DN
谢 谢
小结与思考
知识归纳
1.由不在同一条直线上的三条 首尾依次相接所
组成的图形叫做三角形.
线段
2.三角形的分类:
按角可分为 ;
锐角三角形、直角三角形、钝角三角形
不等边三角形
等腰三角形
等边三角形
底和腰不等的等腰三角形
按边可分为
1. 若一个三角形三个内角度数的比为2:3:4,那么
这个三角形是( )
A.直角三角形 B.锐角三角形
C.钝角三角形 D.等边三角形
【基础训练】
B
40°60°80°
知识归纳
3.三角形 大于第三边,
小于第三边.
任意两边之和
任意两边之差
【基础训练】
如果三角形的两边长分别为3和5,第三边长是偶数
则第三边长可以是( )
A.2 B.3 C.4 D.8
C
两边之差<第三边<两边之和
2<第三边<8
4和6
4.三角形具有 性.
知识归纳
稳定
5.三角形的内角和等于 ;外角和等于 .
180°
360°
6.三角形的外角等于 的和,
三角形的外角大于任何一个 的内角.
与它不相邻的两个内角
与它不相邻
【基础训练】
3. 一副三角尺有两个直角三角形,如右图叠放在一起,
则∠α的度数是( )
A.165° B.120° C.150° D.135°
A
知识归纳
7.三角形中的有关线段:
(1)三角形的高;三角形的中线;三角形的角平分线;
(2)三角形的中位线:连结三角形两边 的线段.
三角形的中位线 于第三边,并且等于 .
中点
平行
第三边的一半
【基础训练】
4. 如图,DE是△ABC的中位线,若BC=8,则DE的
长为 .
4
知识归纳
8.(1)线段垂直平分线上的点到 的距离相等;
(2)到 距离相等的点在这条线段的垂直平
分线上.
线段两端点
线段两端点
100°
【基础训练】
5. 如图,线段AC的垂直平分线交线段AB于点D,
∠A=50°,则∠BDC= .
知识归纳
9.(1)角平分线上的点到 的距离相等;
(2)角的内部到 距离相等的点在这个角的角
平分线上.
角两边
角两边
12
【基础训练】
6. 如图,直角△ABC中,∠C=90°,BD是角平分线,
CD=3,AB=8,则△ABD的面积是 .
E
8
3
3
知识归纳
10.能够完全 的两个三角形叫做全等三角形.
重合
① ② ④
下列说法:①用一张底片冲洗出来的10张1寸相片是全等
形;②我国国旗上的4颗小五角星是全等形; ③所有的
正方形是全等形;④全等形的面积一定相等.
其中正确的是 (填序号)
【基础训练】
√
√
√
知识归纳
11.全等三角形的性质:全等三角形的对应边 ,
对应角 ,对应边上的高 ,对应边上的中
线 ,对应的角平分线 ;全等三角形的
面积 ,周长 .
相等
相等
相等
相等
相等
相等
相等
30°
【基础训练】
8. 如图,△ACB≌△A′CB′,∠ACA′=30°,则
∠BCB′的度数为 .
知识归纳
12.全等三角形的判定方法:
(1)所有三角形都可用的有 ;
(2)直角三角形特有的是 .
SAS、
ASA、AAS、
SSS
HL
DE=AB
【基础训练】
9. 如图,AB∥ED,CD=BF,若△ABC≌△EDF,则还
需要补充的条件可以是 .
答案不唯一
典型例题
例1. (1)如图,点O在△ABC内,且到三边的距离相等.
若∠BOC=120°,则tanA的值为 .
∠BOC=90°+ ∠A
∠BOC=90° ∠A
∠D= ∠A
例1. (2)如图,在Rt△ABC中,∠C=90°,∠CAB的平
分线交BC于D,DE是AB的垂直平分线,垂足
为E.若BC=3,则DE的长为 .
1
例1. (3)如图.三角形纸片ABC中,∠A=65°,∠B=75°
将纸片的一角折叠,使点C落在△ABC内,若
∠1=20°,则∠2的度数为 .
60°
例1. (4)如图,四边形ABCD中,∠BAD=∠BCD=90°,
AB=AD,若四边形ABCD的面积是24cm2,则
AC的长是 cm.
例2. (1)作图发现:如图1, 已知△ABC, 小涵同学以AB , AC
为边向△ABC外作等边△ABD和等△ACE.连接BE, CD.
这时他发现BE与CD的数量关系是 .
(2)拓展探究:如图2, 已知△ABC,小涵同学以AB, AC为边向
外作正方形ABFD和正方形ACGE,连接BE, CD,试判断BE
与CD之间的数量关系,并说明理由.
(3)解决问题:如图3, 要测量池塘两岸相对的两点B, E的距
离已经测得∠ABC=45°, ∠CAE=90°, AB=BC =200米,
AC=AE, 求BE长.
BE=CD
例3. 如图, △ABC中, ∠BAC=90°, AB=AC, AD⊥BC, 垂
足是D, AE平分∠BAD, 交BC于点E. 在△ABC外有一点F
使FA⊥AE, FC⊥BC.
(1)求证:BE=CF;
(2)在AB上取一点M, 使BM=2DE, 连接MC, 交AD于点N,
连接ME. 求证:
①ME⊥BC; ②CM平分∠ACE; ③DE=DN
谢 谢
同课章节目录
- 第一章 全等三角形
- 1.1 全等图形
- 1.2 全等三角形
- 1.3 探索三角形全等的条件
- 数学活动 关于三角形全等的条件
- 第二章 轴对称图形
- 2.1 轴对称与轴对称图形
- 2.2 轴对称的性质
- 2.3 设计轴对称图案
- 2.4 线段、角的轴对称性
- 2.5 等腰三角形的轴对称性
- 数学活动 折纸与证明
- 第三章 勾股定理
- 3.1 勾股定理
- 3.2 勾股定理的逆定理
- 3.3 勾股定理的简单应用
- 数学活动 探寻“勾股数”
- 第四章 实数
- 4.1 平方根
- 4.2 立方根
- 4.3 实数
- 4.4 近似数
- 数学活动 有关“实数”的课题探究
- 第五章 平面直角坐标系
- 5.1 物体位置的确定
- 5.2 平面直角坐标系
- 数学活动 确定藏宝地
- 第六章 一次函数
- 6.1 函数
- 6.2 一次函数
- 6.3 一次函数的图像
- 6.4 用一次函数解决问题
- 6.5 一次函数与二元一次方程
- 6.6 一次函数、一元一次方程和一元一次不等式
- 数学活动 温度计上的一次函数
