2021-2022学年数学人教A版(2019)必修第一册4..2.2指数函数的图象和其性质(第2课时) 课件(共16张)
文档属性
| 名称 | 2021-2022学年数学人教A版(2019)必修第一册4..2.2指数函数的图象和其性质(第2课时) 课件(共16张) |  | |
| 格式 | ppt | ||
| 文件大小 | 1.9MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-10-21 10:12:03 | ||
图片预览





文档简介
(共16张PPT)
4.2 指数函数
4.2.2指数函数的图象和性质
第2课时
复习与回顾
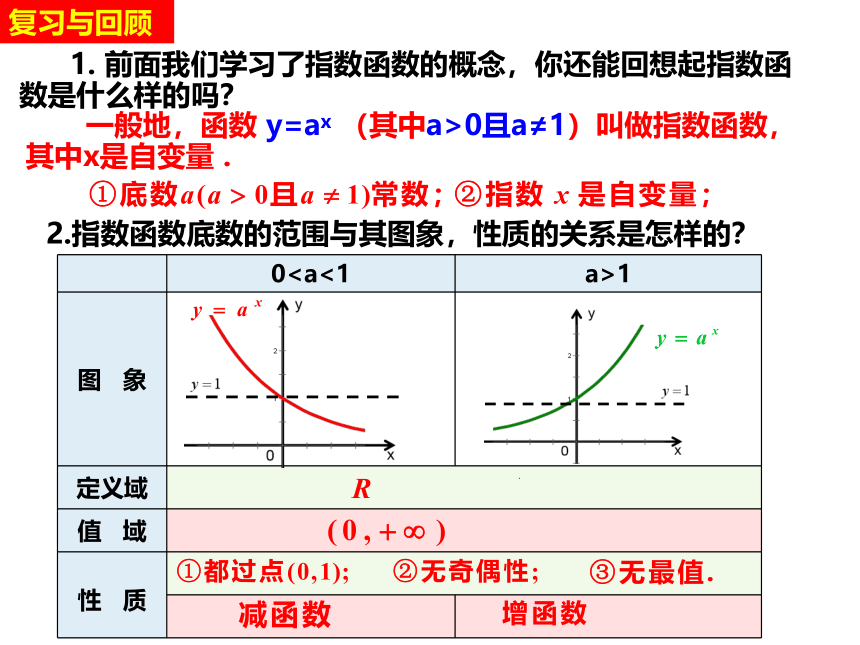
1. 前面我们学习了指数函数的概念,你还能回想起指数函数是什么样的吗?
一般地,函数 y=ax (其中a>0且a≠1)叫做指数函数,其中x是自变量 .
2.指数函数底数的范围与其图象,性质的关系是怎样的?
01
图 象
定义域
值 域
性 质
例析
注:若底数的大小不确定,则应分底数在(0,1)和(1,+∞)讨论,再根据对应指数函数的单调性得出指数的大小。
解指数不等式的主要步骤
化底数
移项
得出指数的大小
解不等式
思考:你能归纳一下解指数不等式的步骤吗?
返回
练习
2.解不等式:
由原不等式得
∴ 1-x<2
解得,x>-1
∴不等式的解集为(-1,+ ∞).
解不等式
化底数
移项
得出指数的大小
简析:
例析
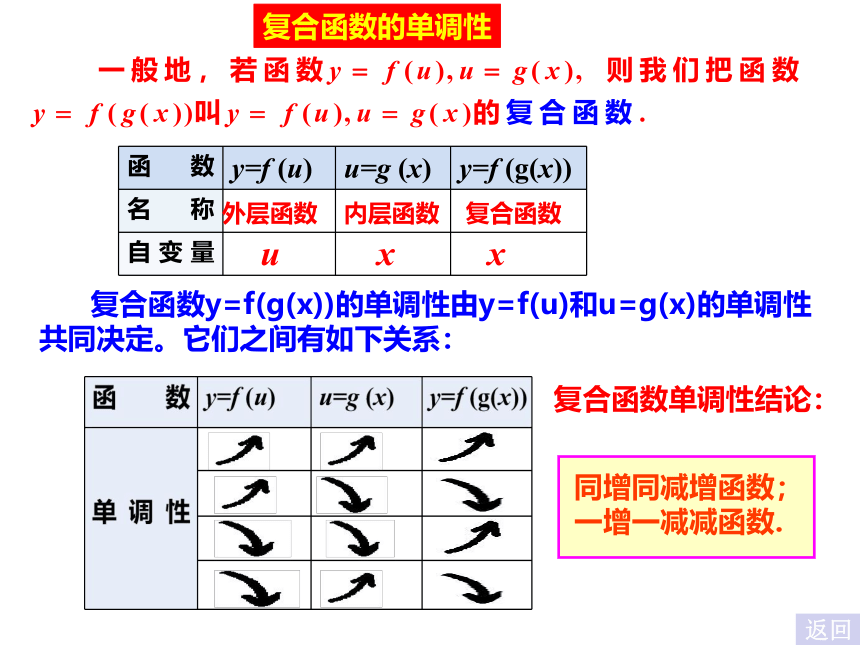
复合函数的单调性
函数 y=f (u) u=g (x) y=f (g(x))
名称
自变量
外层函数
内层函数
复合函数
复合函数y=f(g(x))的单调性由y=f(u)和u=g(x)的单调性共同决定。它们之间有如下关系:
复合函数单调性结论:
同增同减增函数;
一增一减减函数.
返回
思考:如何求函数y=ag(x)(a>0且a≠1)的值域?
①求指数(内层函数g(x))的范围;
②求对应指数函数(外层函数au)的单调性;
③根据指数函数的单调性求函数的值域。
例析
练习
解:(1)
例析
可不可以换为f(-1)=-f(1),为什么?
解:(2)由(1)得
设a>0, 是R上的偶函数,其中e=2.718…
(1)求a的值;
(2)证明:f(x)在(0,+∞)上单调递增.
∵a>0
∴a=1
∴对任意实数x,有f(-x)=f(x)
(1)∵f(x)是R上的偶函数
简析:
练习
x1、x2∈(0,+∞), 且x1又∵ x1、x2∈(0,+∞)
解: (2)
∴f(x)在(0,+∞)上是增函数
设a>0, 是R上的偶函数,其中e=2.718…
(2)证明:f(x)在(0,+∞)上是单调递增.
小结
1.指数函数y=ax (a>0且a≠1)有哪一些性质,请说说其定义域,值域,单调性,奇偶性以及所求指数函数图象的公共点?
4.解指数函数不等式的一般步骤是怎样的?
2.复合函数的单调性如何判定?
函数y=ag(x) (a>0且a≠1)的单调性又如何判定?
3.如何求函数y=ag(x) (a>0且a≠1)的值域?
返回
6.本节(4.2)的基本思想方法有哪一些,能举例说说吗?
5.请你再说说研究函数的基本过程 和方法?
一般与特殊,
数形结合
作业
4.2 指数函数
4.2.2指数函数的图象和性质
第2课时
复习与回顾
1. 前面我们学习了指数函数的概念,你还能回想起指数函数是什么样的吗?
一般地,函数 y=ax (其中a>0且a≠1)叫做指数函数,其中x是自变量 .
2.指数函数底数的范围与其图象,性质的关系是怎样的?
0
图 象
定义域
值 域
性 质
例析
注:若底数的大小不确定,则应分底数在(0,1)和(1,+∞)讨论,再根据对应指数函数的单调性得出指数的大小。
解指数不等式的主要步骤
化底数
移项
得出指数的大小
解不等式
思考:你能归纳一下解指数不等式的步骤吗?
返回
练习
2.解不等式:
由原不等式得
∴ 1-x<2
解得,x>-1
∴不等式的解集为(-1,+ ∞).
解不等式
化底数
移项
得出指数的大小
简析:
例析
复合函数的单调性
函数 y=f (u) u=g (x) y=f (g(x))
名称
自变量
外层函数
内层函数
复合函数
复合函数y=f(g(x))的单调性由y=f(u)和u=g(x)的单调性共同决定。它们之间有如下关系:
复合函数单调性结论:
同增同减增函数;
一增一减减函数.
返回
思考:如何求函数y=ag(x)(a>0且a≠1)的值域?
①求指数(内层函数g(x))的范围;
②求对应指数函数(外层函数au)的单调性;
③根据指数函数的单调性求函数的值域。
例析
练习
解:(1)
例析
可不可以换为f(-1)=-f(1),为什么?
解:(2)由(1)得
设a>0, 是R上的偶函数,其中e=2.718…
(1)求a的值;
(2)证明:f(x)在(0,+∞)上单调递增.
∵a>0
∴a=1
∴对任意实数x,有f(-x)=f(x)
(1)∵f(x)是R上的偶函数
简析:
练习
x1、x2∈(0,+∞), 且x1
解: (2)
∴f(x)在(0,+∞)上是增函数
设a>0, 是R上的偶函数,其中e=2.718…
(2)证明:f(x)在(0,+∞)上是单调递增.
小结
1.指数函数y=ax (a>0且a≠1)有哪一些性质,请说说其定义域,值域,单调性,奇偶性以及所求指数函数图象的公共点?
4.解指数函数不等式的一般步骤是怎样的?
2.复合函数的单调性如何判定?
函数y=ag(x) (a>0且a≠1)的单调性又如何判定?
3.如何求函数y=ag(x) (a>0且a≠1)的值域?
返回
6.本节(4.2)的基本思想方法有哪一些,能举例说说吗?
5.请你再说说研究函数的基本过程 和方法?
一般与特殊,
数形结合
作业
同课章节目录
- 第一章 集合与常用逻辑用语
- 1.1 集合的概念
- 1.2 集合间的基本关系
- 1.3 集合的基本运算
- 1.4 充分条件与必要条件
- 1.5 全称量词与存在量词
- 第二章 一元二次函数、方程和不等式
- 2.1 等式性质与不等式性质
- 2.2 基本不等式
- 2.3 二次函数与一元二次方程、不等式
- 第三章 函数概念与性质
- 3.1 函数的概念及其表示
- 3.2 函数的基本性质
- 3.3 幂函数
- 3.4 函数的应用(一)
- 第四章 指数函数与对数函数
- 4.1 指数
- 4.2 指数函数
- 4.3 对数
- 4.4 对数函数
- 4.5 函数的应用(二)
- 第五章 三角函数
- 5.1 任意角和弧度制
- 5.2 三角函数的概念
- 5.3 诱导公式
- 5.4 三角函数的图象与性质
- 5.5 三角恒等变换
- 5.6 函数 y=Asin( ωx + φ)
- 5.7 三角函数的应用
