2021-2022学年数学人教A版(2019)选择性必修第一册2.1.1直线的倾斜角与斜率课件(共19张)
文档属性
| 名称 | 2021-2022学年数学人教A版(2019)选择性必修第一册2.1.1直线的倾斜角与斜率课件(共19张) |  | |
| 格式 | pptx | ||
| 文件大小 | 1.4MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-10-21 10:15:51 | ||
图片预览




文档简介
(共19张PPT)
直线的倾斜角与斜率
十六、十七世纪,为了描述现实世界的运动变化现象,如行星的运动、平面抛体的运动等,需要对它们的运动轨迹进行精确的代数刻画,运动变化进入了数学,变量观念成为数学中的重要理念.在众多数学家工作的基础上,法国的数学家笛卡尔、费马及其大成,创立了坐标系,用坐标刻画运动变化,这是解析几何的创始.
一、 新课引入
几何的基本元素
几何问题
点和代数的基本对象
数(有序数对或有序数组)
代数问题
几何图形的性质
代数方法
坐标系
引导语:
解析几何的基本内涵和方法是:通过坐标系,把几何的基本元素—点和代数的基本对象—数(有序数对或有序数组)对应起来,在此基础上建立曲线(点的轨迹)的方程,从而把几何问题转化为代数问题,再通过代数方法研究几何图形的性质.
问题1:回顾之前的学习,我们通过坐标系主要研究过哪些类型的图形?所用的研究方法是什么?
建立曲线(点的轨迹)的方程
问题2:直线是最简单的几何图形之一,确定一条直线的几何要素是什么?
二、确定直线位置的几何要素
追问:对于平面直角坐标系中的一条直线(如图所示),如何利用坐标系中确定它的位置?
A
B
O
P
x
y
l1
l2
l3
图2.1-2
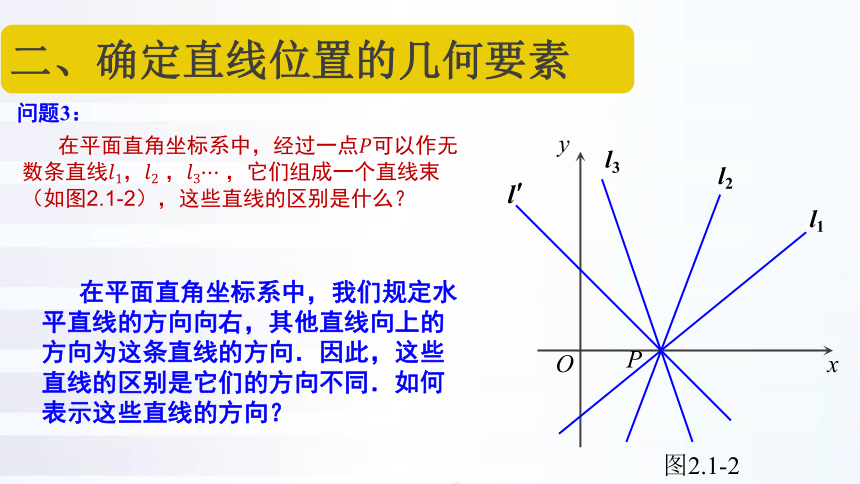
问题3:
在平面直角坐标系中,经过一点可以作无数条直线 它们组成一个直线束(如图2.1-2)这些直线的区别是什么?
二、确定直线位置的几何要素
在平面直角坐标系中,我们规定水平直线的方向向右,其他直线向上的方向为这条直线的方向.因此,这些直线的区别是它们的方向不同.如何表示这些直线的方向?
O
P
x
y
l1
l2
l3
图2.1-2
因此,
我们可以利用这样的角来表示这些直线的方向.
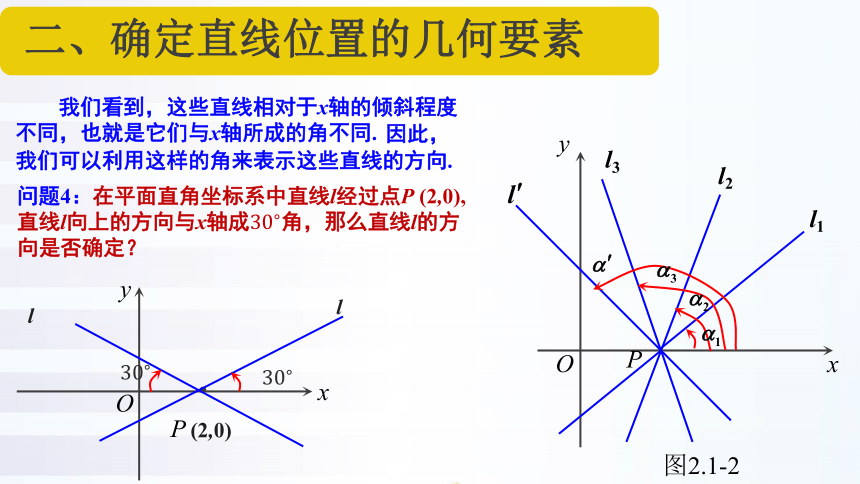
问题4:在平面直角坐标系中直线l经过点P (2,0),直线l向上的方向与x轴成角,那么直线l的方向是否确定?
x
y
P (2,0)
l
l
O
二、确定直线位置的几何要素
我们看到,这些直线相对于x轴的倾斜程度
不同,也就是它们与x轴所成的角不同.
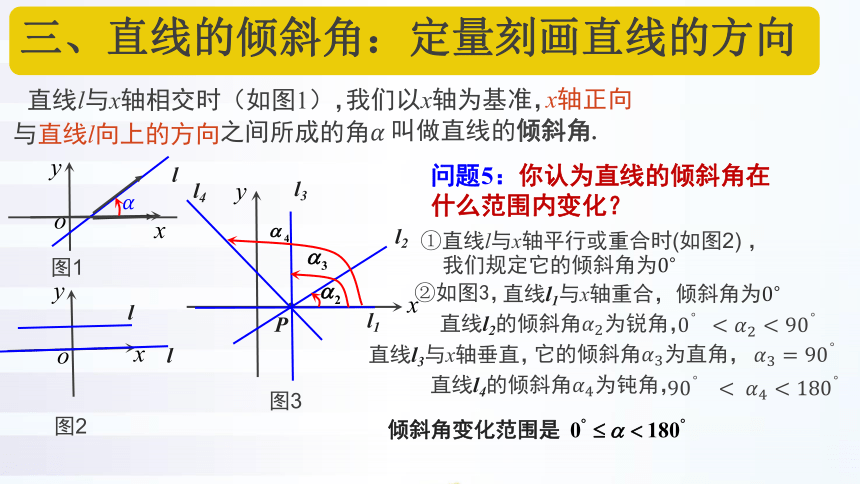
三、直线的倾斜角:定量刻画直线的方向
y
o
x
l
问题5:你认为直线的倾斜角在
什么范围内变化?
x
y
o
l
①直线l与x轴平行或重合时(如图2) ,
l1
图2
y
x
P
l2
图1
l3
l4
图3
②如图3,
直线l2的倾斜角为,
直线l3与x轴垂直,
直线l4的倾斜角为,
倾斜角变化范围是
直线l1与x轴重合,倾斜角为
我们规定它的倾斜角为
之间所成的角
我们以x轴为基准,
叫做直线的倾斜角.
x轴正向
与直线l向上的方向
它的倾斜角为,
l
直线l与x轴相交时(如图1),
在平面直角坐标系中每一条直线
方向相同的 直线,其倾斜程度相同,倾斜角相
等;
方向不同的直线,其倾斜程度
不同,倾斜角不相等.
确定平面直角坐标系中一条直线位置的几何要素可以是:
x
y
O
都有一个确定的倾斜角,
因此,我们可以用倾斜角表示平面直角坐标系中一条直线的倾斜程度,也就表示了直线的方向.
直线上的一个定点以及它的倾斜角
三、直线的倾斜角:定量刻画直线的方向
四、用倾斜角的正切值进一步量化直线的倾斜程度
问题6:设点 是直线l上的两点.由两点确定一条直线可知,直线l由 .因此,直线l的倾斜角一定与 两点的坐标有内在联系.到底具有怎样的联系呢?
下面我们进一步研究研究刻画直线倾斜程度的方法.
y
O
x
,
如图,
且直线l的倾斜角为
由正切函数的定义可知
设是一个任意角,它的终边上任一点P的坐标为( ) ( 0) ,利用三角函数的定义有
( 0)
y
O
x
平移向量到
则点的坐标为(,1)
P
(,1)
且直线也是.
由正切函数的定义,有
如图,
四、用倾斜角的正切值进一步量化直线的倾斜程度
当向量的方向向上时
( , )
平移向量到
则点的坐标为( , )
且直线也是.
由正切函数的定义,有
四、用倾斜角的正切值进一步量化直线的倾斜程度
当向量的方向向上时
( , )
平移向量到
则点的坐标为( , )
且直线也是.
由正切函数的定义,有
=
四、用倾斜角的正切值进一步量化直线的倾斜程度
问题7:直线与轴平行或重合时,式子= 还成立吗?为什么?
和的坐标满足
当直线与轴平行或重合,
倾斜角= ,
= 0,
由图可知,
,
= 0
直线与轴平行或重合时,式子= 仍成立
=
四、用倾斜角的正切值进一步量化直线的倾斜程度
综上可知,直线上两点 的坐标有如下关系:
=
注意公式成立的前提
我们把一条直线的正切值叫做这条直线的
斜率(slope).
斜率常用小写字母,即
k =
四、用倾斜角的正切值进一步量化直线的倾斜程度
问题8:当直线的倾斜角是或时直线的斜率是多少?当直线倾斜角变化时,直线的斜率如何变化的?
k =
上的图象
1.当直线的倾斜角时,
斜率k = = 0,
2.当直线的倾斜角时,
直线与轴平行或重合;
斜率k 不存在,
此时直线存在,与轴平行或重合;
k =
y
O
x
时,
斜率k >0,
且k值随倾斜角的增大而增大;
时,
斜率k 0,
且k值随倾斜角的增大而增大;
四、用倾斜角的正切值进一步量化直线的倾斜程度
反之,当直线与轴平行或重合时,
直线的倾斜角,斜率k = = 0 ;
反之,当直线与轴平行
或重合时,直线的倾斜角时,其斜率不存在 ;
反之,当直线的斜率k >0时,
直线的倾斜角为锐角;
反之,当直线的斜率k <0时,
直线的倾斜角为钝角.
五、用直线的任意两点的坐标表示倾斜角的正切值:斜率
k = ①
如果直线经过两点
=
由公式①,
可得如下的斜率公式:
k =
注意公式成立的前提
我们发现,在平面直角坐标系中,倾斜角
和斜率分别从形和数两个角度刻画了直线对于的倾斜程度.
如果直线经过两点 则直线的斜率
=
五、用直线的任意两点的坐标表示倾斜角的正切值:斜率
问题9:(1)已知直线上的两点 运用上述公式计算直线时,与两点的顺序有关吗?
(2)当直线平行于,或与重合时,上述公式还适用吗?为什么?
(1)计算直线
,
因此与两点的顺序无关.
(2),
直线上的任意两点的横坐标都相等
,
为0,分式无意义,
此时倾斜角为,
因此,斜率公式的适用范围不包含倾斜角的情况,凡在研究直线的斜率问题时,一定要注意斜率存在与不存在两种情况.
斜率公式中的值与 两点在该直线上的位置无关,
即在直线上任取两个不同的点 ,其斜率均不变.
直线的斜率不存在,此时公式不适用
六、建立直线的方向向量与斜率的关系
问题10:
直线,其中 ,你能发现直线的方向向量与斜率之间的关系吗?
我们知道,直线上的向量以及与它平行的向量都是直线的方向向量,
直线的方向向量
当直线与轴不垂直时,
此时向量 也是直线的方向向量,
且它的坐标为 ,
即
=,
其中是直线的斜率.
因此,
若直线的斜率为
它的一个方向向量的坐标为
则
七、例题演练,巩固应用所学知识
图2.1-6
解:
八、课堂小结、布置作业
课堂小结:
了解思想
探究问题
定义倾斜角
形成斜率的概念
反思探究、巩固应用
坐标法对图形的定量化研究
以形的角度刻画直线相对于轴的倾斜程度
以数(坐标)的角度刻画直线相对于轴的倾斜程度
数形结合思想
布置作业:见附件
类比思想
数形结合思想
分类讨论
直线的倾斜角与斜率
十六、十七世纪,为了描述现实世界的运动变化现象,如行星的运动、平面抛体的运动等,需要对它们的运动轨迹进行精确的代数刻画,运动变化进入了数学,变量观念成为数学中的重要理念.在众多数学家工作的基础上,法国的数学家笛卡尔、费马及其大成,创立了坐标系,用坐标刻画运动变化,这是解析几何的创始.
一、 新课引入
几何的基本元素
几何问题
点和代数的基本对象
数(有序数对或有序数组)
代数问题
几何图形的性质
代数方法
坐标系
引导语:
解析几何的基本内涵和方法是:通过坐标系,把几何的基本元素—点和代数的基本对象—数(有序数对或有序数组)对应起来,在此基础上建立曲线(点的轨迹)的方程,从而把几何问题转化为代数问题,再通过代数方法研究几何图形的性质.
问题1:回顾之前的学习,我们通过坐标系主要研究过哪些类型的图形?所用的研究方法是什么?
建立曲线(点的轨迹)的方程
问题2:直线是最简单的几何图形之一,确定一条直线的几何要素是什么?
二、确定直线位置的几何要素
追问:对于平面直角坐标系中的一条直线(如图所示),如何利用坐标系中确定它的位置?
A
B
O
P
x
y
l1
l2
l3
图2.1-2
问题3:
在平面直角坐标系中,经过一点可以作无数条直线 它们组成一个直线束(如图2.1-2)这些直线的区别是什么?
二、确定直线位置的几何要素
在平面直角坐标系中,我们规定水平直线的方向向右,其他直线向上的方向为这条直线的方向.因此,这些直线的区别是它们的方向不同.如何表示这些直线的方向?
O
P
x
y
l1
l2
l3
图2.1-2
因此,
我们可以利用这样的角来表示这些直线的方向.
问题4:在平面直角坐标系中直线l经过点P (2,0),直线l向上的方向与x轴成角,那么直线l的方向是否确定?
x
y
P (2,0)
l
l
O
二、确定直线位置的几何要素
我们看到,这些直线相对于x轴的倾斜程度
不同,也就是它们与x轴所成的角不同.
三、直线的倾斜角:定量刻画直线的方向
y
o
x
l
问题5:你认为直线的倾斜角在
什么范围内变化?
x
y
o
l
①直线l与x轴平行或重合时(如图2) ,
l1
图2
y
x
P
l2
图1
l3
l4
图3
②如图3,
直线l2的倾斜角为,
直线l3与x轴垂直,
直线l4的倾斜角为,
倾斜角变化范围是
直线l1与x轴重合,倾斜角为
我们规定它的倾斜角为
之间所成的角
我们以x轴为基准,
叫做直线的倾斜角.
x轴正向
与直线l向上的方向
它的倾斜角为,
l
直线l与x轴相交时(如图1),
在平面直角坐标系中每一条直线
方向相同的 直线,其倾斜程度相同,倾斜角相
等;
方向不同的直线,其倾斜程度
不同,倾斜角不相等.
确定平面直角坐标系中一条直线位置的几何要素可以是:
x
y
O
都有一个确定的倾斜角,
因此,我们可以用倾斜角表示平面直角坐标系中一条直线的倾斜程度,也就表示了直线的方向.
直线上的一个定点以及它的倾斜角
三、直线的倾斜角:定量刻画直线的方向
四、用倾斜角的正切值进一步量化直线的倾斜程度
问题6:设点 是直线l上的两点.由两点确定一条直线可知,直线l由 .因此,直线l的倾斜角一定与 两点的坐标有内在联系.到底具有怎样的联系呢?
下面我们进一步研究研究刻画直线倾斜程度的方法.
y
O
x
,
如图,
且直线l的倾斜角为
由正切函数的定义可知
设是一个任意角,它的终边上任一点P的坐标为( ) ( 0) ,利用三角函数的定义有
( 0)
y
O
x
平移向量到
则点的坐标为(,1)
P
(,1)
且直线也是.
由正切函数的定义,有
如图,
四、用倾斜角的正切值进一步量化直线的倾斜程度
当向量的方向向上时
( , )
平移向量到
则点的坐标为( , )
且直线也是.
由正切函数的定义,有
四、用倾斜角的正切值进一步量化直线的倾斜程度
当向量的方向向上时
( , )
平移向量到
则点的坐标为( , )
且直线也是.
由正切函数的定义,有
=
四、用倾斜角的正切值进一步量化直线的倾斜程度
问题7:直线与轴平行或重合时,式子= 还成立吗?为什么?
和的坐标满足
当直线与轴平行或重合,
倾斜角= ,
= 0,
由图可知,
,
= 0
直线与轴平行或重合时,式子= 仍成立
=
四、用倾斜角的正切值进一步量化直线的倾斜程度
综上可知,直线上两点 的坐标有如下关系:
=
注意公式成立的前提
我们把一条直线的正切值叫做这条直线的
斜率(slope).
斜率常用小写字母,即
k =
四、用倾斜角的正切值进一步量化直线的倾斜程度
问题8:当直线的倾斜角是或时直线的斜率是多少?当直线倾斜角变化时,直线的斜率如何变化的?
k =
上的图象
1.当直线的倾斜角时,
斜率k = = 0,
2.当直线的倾斜角时,
直线与轴平行或重合;
斜率k 不存在,
此时直线存在,与轴平行或重合;
k =
y
O
x
时,
斜率k >0,
且k值随倾斜角的增大而增大;
时,
斜率k 0,
且k值随倾斜角的增大而增大;
四、用倾斜角的正切值进一步量化直线的倾斜程度
反之,当直线与轴平行或重合时,
直线的倾斜角,斜率k = = 0 ;
反之,当直线与轴平行
或重合时,直线的倾斜角时,其斜率不存在 ;
反之,当直线的斜率k >0时,
直线的倾斜角为锐角;
反之,当直线的斜率k <0时,
直线的倾斜角为钝角.
五、用直线的任意两点的坐标表示倾斜角的正切值:斜率
k = ①
如果直线经过两点
=
由公式①,
可得如下的斜率公式:
k =
注意公式成立的前提
我们发现,在平面直角坐标系中,倾斜角
和斜率分别从形和数两个角度刻画了直线对于的倾斜程度.
如果直线经过两点 则直线的斜率
=
五、用直线的任意两点的坐标表示倾斜角的正切值:斜率
问题9:(1)已知直线上的两点 运用上述公式计算直线时,与两点的顺序有关吗?
(2)当直线平行于,或与重合时,上述公式还适用吗?为什么?
(1)计算直线
,
因此与两点的顺序无关.
(2),
直线上的任意两点的横坐标都相等
,
为0,分式无意义,
此时倾斜角为,
因此,斜率公式的适用范围不包含倾斜角的情况,凡在研究直线的斜率问题时,一定要注意斜率存在与不存在两种情况.
斜率公式中的值与 两点在该直线上的位置无关,
即在直线上任取两个不同的点 ,其斜率均不变.
直线的斜率不存在,此时公式不适用
六、建立直线的方向向量与斜率的关系
问题10:
直线,其中 ,你能发现直线的方向向量与斜率之间的关系吗?
我们知道,直线上的向量以及与它平行的向量都是直线的方向向量,
直线的方向向量
当直线与轴不垂直时,
此时向量 也是直线的方向向量,
且它的坐标为 ,
即
=,
其中是直线的斜率.
因此,
若直线的斜率为
它的一个方向向量的坐标为
则
七、例题演练,巩固应用所学知识
图2.1-6
解:
八、课堂小结、布置作业
课堂小结:
了解思想
探究问题
定义倾斜角
形成斜率的概念
反思探究、巩固应用
坐标法对图形的定量化研究
以形的角度刻画直线相对于轴的倾斜程度
以数(坐标)的角度刻画直线相对于轴的倾斜程度
数形结合思想
布置作业:见附件
类比思想
数形结合思想
分类讨论
