2018-2019学年山东省潍坊市高密市九年级(上)期中数学试卷(Word版 含解析)
文档属性
| 名称 | 2018-2019学年山东省潍坊市高密市九年级(上)期中数学试卷(Word版 含解析) |  | |
| 格式 | doc | ||
| 文件大小 | 447.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 青岛版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-10-20 07:49:15 | ||
图片预览




文档简介
2018-2019学年山东省潍坊市高密市九年级(上)期中数学试卷
一、选择题(本题共12小题,在每小题给出的四个选项中,只有一个是正确的,请把正确的选项选出来。每小题选对得3分,选错、不选或选出的答案超过一个均记0分)
1.(3分)将一元二次方程x2﹣6x﹣5=0化成(x+a)2=c的形式,则c的值为( )
A.﹣4 B.4 C.﹣14 D.14
2.(3分)在△ABC中,∠C=90°,a,b,c分别是∠A、∠B、∠C的对边,则有( )
A.b=a tanA B.b=c sinA C.a=c cosB D.c=a sinA
3.(3分)在一张由复印机复印出来的纸上,一个多边形图案的一条边由原来的1cm变成2cm,那么这次复印出来的多边形图案面积是原来的( )
A.1倍 B.2倍 C.3倍 D.4倍
4.(3分)方程3x2﹣(x﹣1)=0的二次项系数、一次项系数及常数项分别是( )
A.3,,0 B.3,,0 C.3,,﹣1 D.3,,
5.(3分)在△ABC中,若|cosA﹣|+(1﹣tanB)2=0,则∠C的度数是( )
A.45° B.60° C.75° D.105°
6.(3分)如图所示,直线l1∥l2∥l3,下列比例式中错误的是( )
A. B. C. D.
7.(3分)一个公共房门前的台阶高出地面1.2米,台阶拆除后,换成供轮椅行走的斜坡,数据如图所示,则下列关系或结论错误的是( )
A.斜坡AB的坡角是10° B.斜坡AB的坡度是tan10°
C.AC=1.2tan10°米 D.AB=米
8.(3分)如图,△ABC中,点D,E分别在边AB,AC上,下列条件中,不能判定△ABC∽△AED的是( )
A.∠AED=∠B B.∠ADE=∠C C. D.
9.(3分)如图,为测量一棵与地面垂直的树OA的高度,在距离树的底端30米的B处,测得树顶A的仰角∠ABO为α,则树OA的高度为( )
A.米 B.30sinα米 C.30tanα米 D.30cosα米
10.(3分)若关于x的不等式x﹣<1的解集为x<1,则关于x的一元二次方程x2+ax+1=0根的情况是( )
A.有两个相等的实数根 B.有两个不相等的实数根
C.无实数根 D.无法确定
11.(3分)已知m,n是关于x的一元二次方程x2﹣2tx+t2﹣2t+4=0的两实数根,则(m+2)(n+2)的最小值是( )
A.7 B.11 C.12 D.16
12.(3分)如图所示,矩形ABCD中,AB=9,BC=6,若矩形AEFG与矩形ABCD位似,位似比为,则C、F之间的距离为( )
A. B.2 C.3 D.12
二、填空题(每题3分,共24分)
13.(3分)计算:﹣tan45°= .
14.(3分)已知m是关于x的一元二次方程x2﹣x﹣2=0的一个根,则代数式m2﹣m= .
15.(3分)如图,△ABC∽△DEF,∠A=90°,AB=9,AC=DE=6,则DF= .
16.(3分)如果等腰三角形的底角为30°,底边长为6cm,那么这个三角形的面积为 cm2.
17.(3分)如图所示,△ABC的顶点是正方形网格的格点,则sinA的值为 .
18.(3分)如图,在矩形ABCD中,AB=4,BC=6,M是边BC的中点,DE⊥AM,垂足为E,则DE= .
19.(3分)如图,小明同学用自制的直角三角形纸板DEF测量树的高度AB,他调整自己的位置,设法使斜边DF保持水平,并且边DE与点B在同一直线上.已知纸板的两条直角边DE=0.4m,EF=0.2cm,测得边DF离地面的高度AC=1.5m,CD=8m,则树的高度为 m.
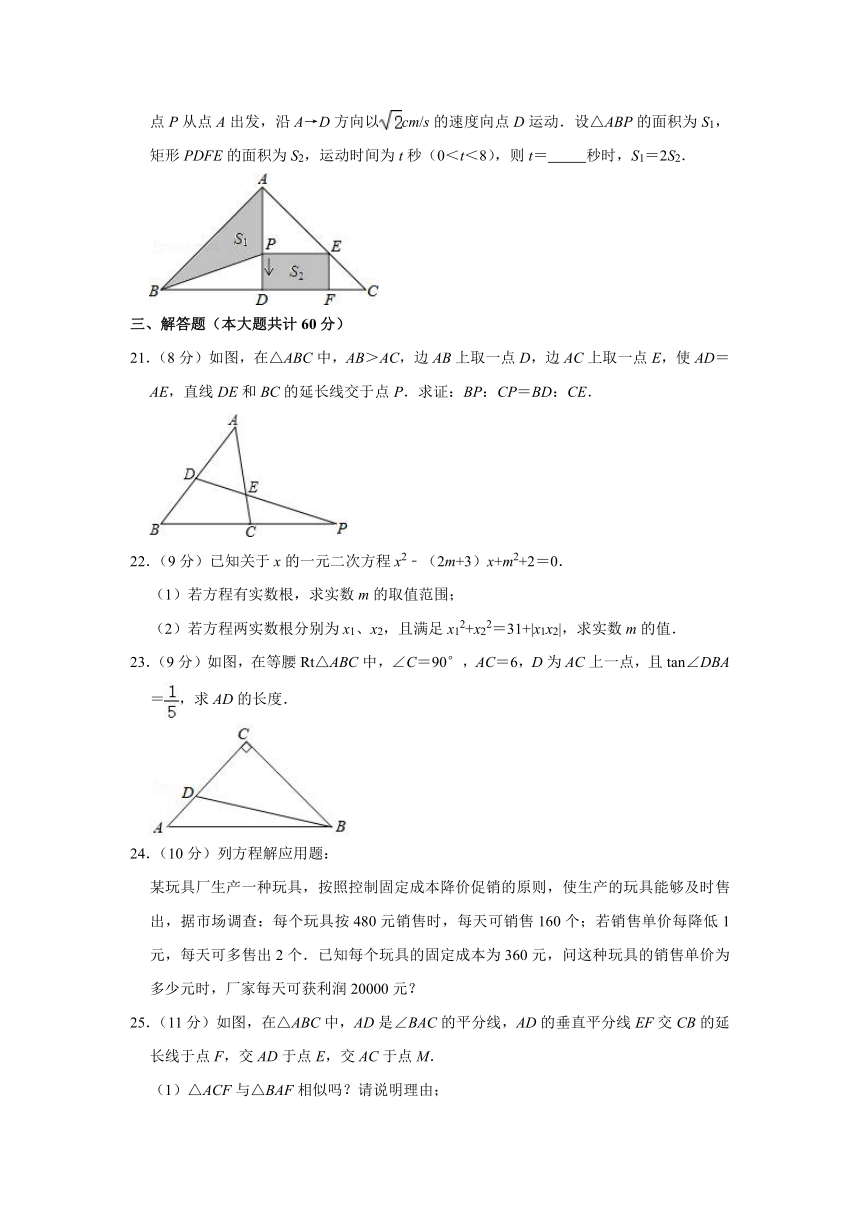
20.(3分)如图,在Rt△ABC中,∠BAC=90°,AB=AC=16cm,AD为BC边上的高.动点P从点A出发,沿A→D方向以cm/s的速度向点D运动.设△ABP的面积为S1,矩形PDFE的面积为S2,运动时间为t秒(0<t<8),则t= 秒时,S1=2S2.
三、解答题(本大题共计60分)
21.(8分)如图,在△ABC中,AB>AC,边AB上取一点D,边AC上取一点E,使AD=AE,直线DE和BC的延长线交于点P.求证:BP:CP=BD:CE.
22.(9分)已知关于x的一元二次方程x2﹣(2m+3)x+m2+2=0.
(1)若方程有实数根,求实数m的取值范围;
(2)若方程两实数根分别为x1、x2,且满足x12+x22=31+|x1x2|,求实数m的值.
23.(9分)如图,在等腰Rt△ABC中,∠C=90°,AC=6,D为AC上一点,且tan∠DBA=,求AD的长度.
24.(10分)列方程解应用题:
某玩具厂生产一种玩具,按照控制固定成本降价促销的原则,使生产的玩具能够及时售出,据市场调查:每个玩具按480元销售时,每天可销售160个;若销售单价每降低1元,每天可多售出2个.已知每个玩具的固定成本为360元,问这种玩具的销售单价为多少元时,厂家每天可获利润20000元?
25.(11分)如图,在△ABC中,AD是∠BAC的平分线,AD的垂直平分线EF交CB的延长线于点F,交AD于点E,交AC于点M.
(1)△ACF与△BAF相似吗?请说明理由;
(2)如果AF=6,BD=2,AC=4,求DC和AM的长.
26.(13分)如图,港口B位于港口O正西方向120海里处,小岛C位于港口O北偏西60°的方向.一艘科学考察船从港口O出发,沿北偏西30°的OA方向以20海里/小时的速度驶离港口O.同时一艘快艇从港口B出发,沿北偏东30°的方向以60海里/小时的速度驶向小岛C,在小岛C用1小时装补给物资后,立即按原来的速度给考察船送去.
(1)快艇从港口B到小岛C需要多少时间?
(2)快艇从小岛C出发后最少需要多少时间才能和考察船相遇?
2018-2019学年山东省潍坊市高密市九年级(上)期中数学试卷
参考答案与试题解析
一、选择题(本题共12小题,在每小题给出的四个选项中,只有一个是正确的,请把正确的选项选出来。每小题选对得3分,选错、不选或选出的答案超过一个均记0分)
1.(3分)将一元二次方程x2﹣6x﹣5=0化成(x+a)2=c的形式,则c的值为( )
A.﹣4 B.4 C.﹣14 D.14
【分析】将常数项移到方程的右边,两边都加上一次项系数一半的平方配成完全平方式后即可得出答案.
【解答】解:∵x2﹣6x﹣5=0,
∴x2﹣6x=5,
则x2﹣6x+9=5+9,即(x﹣3)2=14,
∴c=14,
故选:D.
2.(3分)在△ABC中,∠C=90°,a,b,c分别是∠A、∠B、∠C的对边,则有( )
A.b=a tanA B.b=c sinA C.a=c cosB D.c=a sinA
【分析】根据锐角三角函数的定义判断.
【解答】解:在△ABC中,∠C=90°,a,b,c分别是∠A、∠B、∠C的对边,
tanA=,则a=b tanA,A错误;
sinA=,则a=c sinA,B错误;
cosB=,则a=c cosB,C正确;
sinA=,则a=c sinA,D错误;
故选:C.
3.(3分)在一张由复印机复印出来的纸上,一个多边形图案的一条边由原来的1cm变成2cm,那么这次复印出来的多边形图案面积是原来的( )
A.1倍 B.2倍 C.3倍 D.4倍
【分析】复印前后的多边形按照比例放大与缩小,因此它们是相似多边形,本题按照相似多边形的性质求解.
【解答】解:由题意可知,相似多边形的边长之比=相似比=1:2,所以面积之比=(1:2)2=1:4.
故选:D.
4.(3分)方程3x2﹣(x﹣1)=0的二次项系数、一次项系数及常数项分别是( )
A.3,,0 B.3,,0 C.3,,﹣1 D.3,,
【分析】先化成一元二次方程的一般形式,再找出二次项系数、一次项系数、常数项即可.
【解答】解:∵3x2﹣(x﹣1)=0,
∴3x2﹣x+=0,
∴方程3x2﹣(x﹣1)=0的二次项系数、一次项系数及常数项分别是3,﹣,,
故选:D.
5.(3分)在△ABC中,若|cosA﹣|+(1﹣tanB)2=0,则∠C的度数是( )
A.45° B.60° C.75° D.105°
【分析】根据非负数的性质可得出cosA及tanB的值,继而可得出A和B的度数,根据三角形的内角和定理可得出∠C的度数.
【解答】解:由题意,得 cosA=,tanB=1,
∴∠A=60°,∠B=45°,
∴∠C=180°﹣∠A﹣∠B=180°﹣60°﹣45°=75°.
故选:C.
6.(3分)如图所示,直线l1∥l2∥l3,下列比例式中错误的是( )
A. B. C. D.
【分析】由平行线分线段成比例的性质,分别对选项进行判断即可.
【解答】解:A.∵l1∥l2∥l3,
∴=,
故A不符合题意;
B..∵l1∥l2∥l3,
∴=,
故A不符合题意;
C.∵l1∥l2∥l3,
∴=,
故C符合题意;
D.∵l1∥l2∥l3,
∴=,
故D不符合题意;
故选:C.
7.(3分)一个公共房门前的台阶高出地面1.2米,台阶拆除后,换成供轮椅行走的斜坡,数据如图所示,则下列关系或结论错误的是( )
A.斜坡AB的坡角是10° B.斜坡AB的坡度是tan10°
C.AC=1.2tan10°米 D.AB=米
【分析】先根据坡度,坡角判断出A,B,再用锐角三角函数判断出C,D即可.
【解答】解:根据坡角的定义得,斜坡AB的坡角是10°,此结论正确;即:A正确,
根据坡度的定义得,斜坡AB的坡度是tan10°,此结论正确;即:B正确,
在Rt△ABC中,∠BAC=10°,BC=1.2,
∴tan∠BAC==,
∴AC=米,此结论错误,即:C错误;
在Rt△ABC中,∠BAC=10°,BC=1.2,
∴sin∠BAC==,
∴AB=米,此结论正确,即:D正确.
故选:C.
8.(3分)如图,△ABC中,点D,E分别在边AB,AC上,下列条件中,不能判定△ABC∽△AED的是( )
A.∠AED=∠B B.∠ADE=∠C C. D.
【分析】根据相似三角形的判定定理对各选项进行逐一判断即可.
【解答】解:A、∠B=∠AED,∠A=∠A,则可判断△ADE∽△ACB,故A选项不符合题意;
B、∠ADE=∠C,∠A=∠A,则可判断△ADE∽△ACB,故B选项不符合题意;
C、=且夹角∠A=∠A,则能判定△ADE∽△ACB,故C选项不符合题意;
D、=,不能确定△ADE∽△ACB,故D选项符合题意.
故选:D.
9.(3分)如图,为测量一棵与地面垂直的树OA的高度,在距离树的底端30米的B处,测得树顶A的仰角∠ABO为α,则树OA的高度为( )
A.米 B.30sinα米 C.30tanα米 D.30cosα米
【分析】根据题意,在Rt△ABO中,BO=30米,∠ABO为α,利用三角函数求解.
【解答】解:在Rt△ABO中,
∵BO=30米,∠ABO为α,
∴AO=BOtanα=30tanα(米).
故选:C.
10.(3分)若关于x的不等式x﹣<1的解集为x<1,则关于x的一元二次方程x2+ax+1=0根的情况是( )
A.有两个相等的实数根 B.有两个不相等的实数根
C.无实数根 D.无法确定
【分析】先解不等式,再利用不等式的解集得到1+=1,则a=0,然后计算判别式的值,最后根据判别式的意义判断方程根的情况.
【解答】解:解不等式x﹣<1得x<1+,
而不等式x﹣<1的解集为x<1,
所以1+=1,解得a=0,
又因为Δ=a2﹣4=﹣4,
所以关于x的一元二次方程x2+ax+1=0没有实数根.
故选:C.
11.(3分)已知m,n是关于x的一元二次方程x2﹣2tx+t2﹣2t+4=0的两实数根,则(m+2)(n+2)的最小值是( )
A.7 B.11 C.12 D.16
【分析】由根与系数的关系可得出m+n=2t、mn=t2﹣2t+4,将其代入(m+2)(n+2)=mn+2(m+n)+4中可得出(m+2)(n+2)=(t+1)2+7,由方程有两个实数根结合根的判别式可求出t的取值范围,再根据二次函数的性质即可得出(m+2)(n+2)的最小值.
【解答】解:∵m,n是关于x的一元二次方程x2﹣2tx+t2﹣2t+4=0的两实数根,
∴m+n=2t,mn=t2﹣2t+4,
∴(m+2)(n+2)=mn+2(m+n)+4=t2+2t+8=(t+1)2+7.
∵方程有两个实数根,
∴Δ=(﹣2t)2﹣4(t2﹣2t+4)=8t﹣16≥0,
∴t≥2,
∴(t+1)2+7≥(2+1)2+7=16.
故选:D.
12.(3分)如图所示,矩形ABCD中,AB=9,BC=6,若矩形AEFG与矩形ABCD位似,位似比为,则C、F之间的距离为( )
A. B.2 C.3 D.12
【分析】连接AF、FC,根据位似变换的性质得到A、F、C在同一条直线上,根据勾股定理求出AC,根据位似比计算即可.
【解答】解:连接AF、FC,
∵矩形AEFG与矩形ABCD位似,
∴A、F、C在同一条直线上,EF∥BC,
∵AB=9,BC=6,
∴AC==3,
∵矩形AEFG与矩形ABCD位似,位似比为,
∴CF=AC=,
故选:A.
二、填空题(每题3分,共24分)
13.(3分)计算:﹣tan45°= 0 .
【分析】根据45°的三角函数值代入计算即可.
【解答】解:原式=﹣1
=1﹣1
=0,
故答案为:0.
14.(3分)已知m是关于x的一元二次方程x2﹣x﹣2=0的一个根,则代数式m2﹣m= 2 .
【分析】将x=m代入原方程即可求m2+m的值.
【解答】解:将x=m代入方程x2﹣x﹣2=0,
得m2﹣m﹣2=0,
即m2﹣m=2,
故答案为:2.
15.(3分)如图,△ABC∽△DEF,∠A=90°,AB=9,AC=DE=6,则DF= 4 .
【分析】利用相似三角形的对应边的比相等列式计算即可.
【解答】解:∵△ABC∽△DEF,
∴AB:DE=AC:DF,
∵AB=9,AC=DE=6,
∴9:6=6:DF,
解得:x=4,
故答案为:4.
16.(3分)如果等腰三角形的底角为30°,底边长为6cm,那么这个三角形的面积为 cm2.
【分析】作底边上的高.运用等腰三角形的性质及三角函数定义分别求三角形的高和底边长,代入公式计算求解.
【解答】解:如图,△ABC,AB=AC,∠B=∠C=30°,BC=cm,作底边BC上的高AD.
∴BD=CD=cm,
∴AD=cm,
∴S△ABC=BC AD=.
故答案为.
17.(3分)如图所示,△ABC的顶点是正方形网格的格点,则sinA的值为 .
【分析】连接CE,求出CE⊥AB,根据勾股定理求出CA,在Rt△AEC中,根据锐角三角函数定义求出即可.
【解答】解:
连接CE,
∵根据图形可知DC=1,AD=3,AC==,
BE=CE==,∠EBC=∠ECB=45°,
∴CE⊥AB,
∴sinA===,
故答案为:.
18.(3分)如图,在矩形ABCD中,AB=4,BC=6,M是边BC的中点,DE⊥AM,垂足为E,则DE= .
【分析】先根据矩形的性质得到AD=BC=6,∠B=90°,AD∥BC,再利用勾股定理计算出AM=5,然后证明△ADE∽△MAB,从而利用相似比计算出DE的长.
【解答】解:∵四边形ABCD为矩形,
∴AD=BC=6,∠B=90°,AD∥BC,
∴∠DAM=∠AMB,
∵M是边BC的中点,
∴BM=BC=3,
在Rt△ABM中,AM===5,
∵DE⊥AM,
∴∠AED=90°,
∵∠DAE=∠AMB,∠AED=∠B,
∴△ADE∽△MAB,
∴=,即=,
∴DE=.
故答案为.
19.(3分)如图,小明同学用自制的直角三角形纸板DEF测量树的高度AB,他调整自己的位置,设法使斜边DF保持水平,并且边DE与点B在同一直线上.已知纸板的两条直角边DE=0.4m,EF=0.2cm,测得边DF离地面的高度AC=1.5m,CD=8m,则树的高度为 5.5 m.
【分析】利用Rt△DEF和Rt△BCD相似求得BC的长后加上边DF到地面的高度CA,即可求得树高AB.
【解答】解:∵∠DEF=∠DCB=90°,∠D=∠D,
∴△DEF∽△DCB
∴=,
∵DE=0.4m,EF=0.2m,CD=8m,
∴=,
∴CB=4(m),
∴AB=AC+BC=1.5+4=5.5(m).
答:树高为5.5m,
故答案为:5.5.
20.(3分)如图,在Rt△ABC中,∠BAC=90°,AB=AC=16cm,AD为BC边上的高.动点P从点A出发,沿A→D方向以cm/s的速度向点D运动.设△ABP的面积为S1,矩形PDFE的面积为S2,运动时间为t秒(0<t<8),则t= 6 秒时,S1=2S2.
【分析】利用三角形的面积公式以及矩形的面积公式,表示出S1和S2,然后根据S1=2S2,即可列方程求解.
【解答】解:∵Rt△ABC中,∠BAC=90°,AB=AC=16cm,AD为BC边上的高,
∴AD=BD=CD=8cm,
又∵AP=t,
则S1=AP BD=×8×t=8t,PD=8﹣t,
∵PE∥BC,
∴△APE∽△ADC,
∴,
∴PE=AP=t,
∴S2=PD PE=(8﹣t) t,
∵S1=2S2,
∴8t=2(8﹣t) t,
解得:t=6.
故答案是:6.
三、解答题(本大题共计60分)
21.(8分)如图,在△ABC中,AB>AC,边AB上取一点D,边AC上取一点E,使AD=AE,直线DE和BC的延长线交于点P.求证:BP:CP=BD:CE.
【分析】如图,过点B作BF∥AC交PD延长线于点F.则△PCE∽△PBF,所以该相似三角形的对应边成比例,即=.根据平行线的性质,等腰三角形的性质以及对顶角的定义得
BF=BD.则=,故BP:CP=BD:CE.
【解答】证明:如图,过点B作BF∥AC交PD延长线于点F.则△PCE∽△PBF,
∴=.
∵BF∥AC,
∴∠1=∠2.
又∵AD=AE,
∴∠2=∠4,
∠1=∠3=∠4,
∴BF=BD.
∴=,
∴BP:CP=BD:CE.
22.(9分)已知关于x的一元二次方程x2﹣(2m+3)x+m2+2=0.
(1)若方程有实数根,求实数m的取值范围;
(2)若方程两实数根分别为x1、x2,且满足x12+x22=31+|x1x2|,求实数m的值.
【分析】(1)利用判别式的意义得到(2m+3)2﹣4(m2+2)≥0,然后解不等式即可;
(2)根据题意x1+x2=2m+3,x1x2=m2+2,由条件得x12+x22=31+x1x2,再利用完全平方公式得(x1+x2)2﹣3x1x2﹣31=0,所以2m+3)2﹣3(m2+2)﹣31=0,然后解关于m的方程,最后利用m的范围确定满足条件的m的值.
【解答】解:(1)根据题意得(2m+3)2﹣4(m2+2)≥0,
解得m≥﹣;
(2)根据题意x1+x2=2m+3,x1x2=m2+2,
因为x1x2=m2+2>0,
所以x12+x22=31+x1x2,
即(x1+x2)2﹣3x1x2﹣31=0,
所以(2m+3)2﹣3(m2+2)﹣31=0,
整理得m2+12m﹣28=0,解得m1=﹣14,m2=2,
而m≥﹣;
所以m=2.
23.(9分)如图,在等腰Rt△ABC中,∠C=90°,AC=6,D为AC上一点,且tan∠DBA=,求AD的长度.
【分析】过点D作DH⊥AB于点H,根据等腰直角三角形的性质,勾股定理以及锐角三角形函数的定义即可求出答案.
【解答】解:过点D作DH⊥AB于点H,
∵等腰三角形ABC,∠C=90°,
∴∠A=45°,
∴AH=DH,
设AH=x,
∴DH=x,
∵tan∠DBA=,
∴BH=5x,
∴AB=6x,
∵AC=6,
∴由勾股定理可知:AB=6,
∴x=,
∴AH=DH=,
∴由勾股定理可知:AD=2.
24.(10分)列方程解应用题:
某玩具厂生产一种玩具,按照控制固定成本降价促销的原则,使生产的玩具能够及时售出,据市场调查:每个玩具按480元销售时,每天可销售160个;若销售单价每降低1元,每天可多售出2个.已知每个玩具的固定成本为360元,问这种玩具的销售单价为多少元时,厂家每天可获利润20000元?
【分析】根据单件利润×销售量=总利润,列方程求解即可.
【解答】解:设销售单价为x元,
由题意,得:(x﹣360)[160+2(480﹣x)]=20000,
整理,得:x2﹣920x+211600=0,
解得:x1=x2=460,
答:这种玩具的销售单价为460元时,厂家每天可获利润20000元.
25.(11分)如图,在△ABC中,AD是∠BAC的平分线,AD的垂直平分线EF交CB的延长线于点F,交AD于点E,交AC于点M.
(1)△ACF与△BAF相似吗?请说明理由;
(2)如果AF=6,BD=2,AC=4,求DC和AM的长.
【分析】(1)首先证明∠DAF=∠ADF,结合平分线的性质以及角角之间的数量关系得到∠BAF=∠C,再根据∠AFB=∠AFC即可判定△ACF与△BAF相似;
(2)连接DM,首先求出BF的长度,利用△ACF与△BAF相似,得到,结合题干数据求出CF的长度,进而求出CD的长度,由∠DAM=∠ADM,∠BAD=∠CAD,得到∠BAD=∠ADM,进而得到DM∥BA,即,结合线段之间的数量关系即求出AM的长.
【解答】解:(1)△ACF∽△BAF.
∵EF垂直平分AD,
∴AF=DF,
∴∠DAF=∠ADF.
∵AD平分∠BAC,
∴∠BAD=∠CAD,
∵∠DAF=∠BAF+∠BAD,∠ADF=∠C+∠CAD,
∴∠BAF=∠C.
又∵∠AFB=∠AFC,
∴△ACF∽△BAF.
(2)连接DM.
∵EF垂直平分AD,
∴DM=AM,DF=AF=6.
∵BD=2.
∴BF=6﹣2=4.
由(1)知,△ACF∽△BAF,
∴.
∴AF2=BF CF,即36=4CF.解得CF=9.
∴CD=CF﹣FD=9﹣6=3.
∵∠DAM=∠ADM,∠BAD=∠CAD,
∴∠BAD=∠ADM.
∴DM∥BA.
∴.
∴.
∵BC=DC+BD=3+2=5.
即.
∴AM=.
26.(13分)如图,港口B位于港口O正西方向120海里处,小岛C位于港口O北偏西60°的方向.一艘科学考察船从港口O出发,沿北偏西30°的OA方向以20海里/小时的速度驶离港口O.同时一艘快艇从港口B出发,沿北偏东30°的方向以60海里/小时的速度驶向小岛C,在小岛C用1小时装补给物资后,立即按原来的速度给考察船送去.
(1)快艇从港口B到小岛C需要多少时间?
(2)快艇从小岛C出发后最少需要多少时间才能和考察船相遇?
【分析】(1)要求B到C的时间,已知其速度,则只要求得BC的路程,再利用路程公式即可求得所需的时间.
(2)过C作CH⊥OA,垂足为H.设快艇从C岛出发后最少要经过x小时才能和考察船在OA上的D处相遇,则CD=60x,OD=20(x+2).根据直角三角形的性质可解得x的值,从而求得快艇从小岛C出发后和考察船相遇的最短的时间.
【解答】解:(1)由题意可知:∠CBO=60°,∠COB=30度.
∴∠BCO=90度.
在Rt△BCO中,
∵OB=120,
∴BC=60,OC=60.
∴快艇从港口B到小岛C的时间为:60÷60=1(小时).
(2)设快艇从C岛出发后最少要经过x小时才能和考察船在
OA上的D处相遇,则CD=60x.
过点D作DE⊥CO于点E,
∵考察船与快艇是同时出发,
∵快艇从港口B到小岛C的时间是1小时,在小岛C用1小时装补给物资,
∴考察船从O到D行驶了(x+2)小时,
∴OD=20(x+2).
过C作CH⊥OA,垂足为H,
在△OHC中,
∵∠COH=30°,OB=120,
∴CO=60,
∴CH=30,OH=90.
∴DH=OH﹣OD=90﹣20(x+2)=50﹣20x.
在Rt△CHD中,CH2+DH2=CD2,
∴+(50﹣20x)2=(60x)2.
整理得:8x2+5x﹣13=0.
解得:x1=1,x2=﹣.
∵x>0,
∴x=1.
答:快艇从小岛C出发后最少需要1小时才能和考察船相遇.
一、选择题(本题共12小题,在每小题给出的四个选项中,只有一个是正确的,请把正确的选项选出来。每小题选对得3分,选错、不选或选出的答案超过一个均记0分)
1.(3分)将一元二次方程x2﹣6x﹣5=0化成(x+a)2=c的形式,则c的值为( )
A.﹣4 B.4 C.﹣14 D.14
2.(3分)在△ABC中,∠C=90°,a,b,c分别是∠A、∠B、∠C的对边,则有( )
A.b=a tanA B.b=c sinA C.a=c cosB D.c=a sinA
3.(3分)在一张由复印机复印出来的纸上,一个多边形图案的一条边由原来的1cm变成2cm,那么这次复印出来的多边形图案面积是原来的( )
A.1倍 B.2倍 C.3倍 D.4倍
4.(3分)方程3x2﹣(x﹣1)=0的二次项系数、一次项系数及常数项分别是( )
A.3,,0 B.3,,0 C.3,,﹣1 D.3,,
5.(3分)在△ABC中,若|cosA﹣|+(1﹣tanB)2=0,则∠C的度数是( )
A.45° B.60° C.75° D.105°
6.(3分)如图所示,直线l1∥l2∥l3,下列比例式中错误的是( )
A. B. C. D.
7.(3分)一个公共房门前的台阶高出地面1.2米,台阶拆除后,换成供轮椅行走的斜坡,数据如图所示,则下列关系或结论错误的是( )
A.斜坡AB的坡角是10° B.斜坡AB的坡度是tan10°
C.AC=1.2tan10°米 D.AB=米
8.(3分)如图,△ABC中,点D,E分别在边AB,AC上,下列条件中,不能判定△ABC∽△AED的是( )
A.∠AED=∠B B.∠ADE=∠C C. D.
9.(3分)如图,为测量一棵与地面垂直的树OA的高度,在距离树的底端30米的B处,测得树顶A的仰角∠ABO为α,则树OA的高度为( )
A.米 B.30sinα米 C.30tanα米 D.30cosα米
10.(3分)若关于x的不等式x﹣<1的解集为x<1,则关于x的一元二次方程x2+ax+1=0根的情况是( )
A.有两个相等的实数根 B.有两个不相等的实数根
C.无实数根 D.无法确定
11.(3分)已知m,n是关于x的一元二次方程x2﹣2tx+t2﹣2t+4=0的两实数根,则(m+2)(n+2)的最小值是( )
A.7 B.11 C.12 D.16
12.(3分)如图所示,矩形ABCD中,AB=9,BC=6,若矩形AEFG与矩形ABCD位似,位似比为,则C、F之间的距离为( )
A. B.2 C.3 D.12
二、填空题(每题3分,共24分)
13.(3分)计算:﹣tan45°= .
14.(3分)已知m是关于x的一元二次方程x2﹣x﹣2=0的一个根,则代数式m2﹣m= .
15.(3分)如图,△ABC∽△DEF,∠A=90°,AB=9,AC=DE=6,则DF= .
16.(3分)如果等腰三角形的底角为30°,底边长为6cm,那么这个三角形的面积为 cm2.
17.(3分)如图所示,△ABC的顶点是正方形网格的格点,则sinA的值为 .
18.(3分)如图,在矩形ABCD中,AB=4,BC=6,M是边BC的中点,DE⊥AM,垂足为E,则DE= .
19.(3分)如图,小明同学用自制的直角三角形纸板DEF测量树的高度AB,他调整自己的位置,设法使斜边DF保持水平,并且边DE与点B在同一直线上.已知纸板的两条直角边DE=0.4m,EF=0.2cm,测得边DF离地面的高度AC=1.5m,CD=8m,则树的高度为 m.
20.(3分)如图,在Rt△ABC中,∠BAC=90°,AB=AC=16cm,AD为BC边上的高.动点P从点A出发,沿A→D方向以cm/s的速度向点D运动.设△ABP的面积为S1,矩形PDFE的面积为S2,运动时间为t秒(0<t<8),则t= 秒时,S1=2S2.
三、解答题(本大题共计60分)
21.(8分)如图,在△ABC中,AB>AC,边AB上取一点D,边AC上取一点E,使AD=AE,直线DE和BC的延长线交于点P.求证:BP:CP=BD:CE.
22.(9分)已知关于x的一元二次方程x2﹣(2m+3)x+m2+2=0.
(1)若方程有实数根,求实数m的取值范围;
(2)若方程两实数根分别为x1、x2,且满足x12+x22=31+|x1x2|,求实数m的值.
23.(9分)如图,在等腰Rt△ABC中,∠C=90°,AC=6,D为AC上一点,且tan∠DBA=,求AD的长度.
24.(10分)列方程解应用题:
某玩具厂生产一种玩具,按照控制固定成本降价促销的原则,使生产的玩具能够及时售出,据市场调查:每个玩具按480元销售时,每天可销售160个;若销售单价每降低1元,每天可多售出2个.已知每个玩具的固定成本为360元,问这种玩具的销售单价为多少元时,厂家每天可获利润20000元?
25.(11分)如图,在△ABC中,AD是∠BAC的平分线,AD的垂直平分线EF交CB的延长线于点F,交AD于点E,交AC于点M.
(1)△ACF与△BAF相似吗?请说明理由;
(2)如果AF=6,BD=2,AC=4,求DC和AM的长.
26.(13分)如图,港口B位于港口O正西方向120海里处,小岛C位于港口O北偏西60°的方向.一艘科学考察船从港口O出发,沿北偏西30°的OA方向以20海里/小时的速度驶离港口O.同时一艘快艇从港口B出发,沿北偏东30°的方向以60海里/小时的速度驶向小岛C,在小岛C用1小时装补给物资后,立即按原来的速度给考察船送去.
(1)快艇从港口B到小岛C需要多少时间?
(2)快艇从小岛C出发后最少需要多少时间才能和考察船相遇?
2018-2019学年山东省潍坊市高密市九年级(上)期中数学试卷
参考答案与试题解析
一、选择题(本题共12小题,在每小题给出的四个选项中,只有一个是正确的,请把正确的选项选出来。每小题选对得3分,选错、不选或选出的答案超过一个均记0分)
1.(3分)将一元二次方程x2﹣6x﹣5=0化成(x+a)2=c的形式,则c的值为( )
A.﹣4 B.4 C.﹣14 D.14
【分析】将常数项移到方程的右边,两边都加上一次项系数一半的平方配成完全平方式后即可得出答案.
【解答】解:∵x2﹣6x﹣5=0,
∴x2﹣6x=5,
则x2﹣6x+9=5+9,即(x﹣3)2=14,
∴c=14,
故选:D.
2.(3分)在△ABC中,∠C=90°,a,b,c分别是∠A、∠B、∠C的对边,则有( )
A.b=a tanA B.b=c sinA C.a=c cosB D.c=a sinA
【分析】根据锐角三角函数的定义判断.
【解答】解:在△ABC中,∠C=90°,a,b,c分别是∠A、∠B、∠C的对边,
tanA=,则a=b tanA,A错误;
sinA=,则a=c sinA,B错误;
cosB=,则a=c cosB,C正确;
sinA=,则a=c sinA,D错误;
故选:C.
3.(3分)在一张由复印机复印出来的纸上,一个多边形图案的一条边由原来的1cm变成2cm,那么这次复印出来的多边形图案面积是原来的( )
A.1倍 B.2倍 C.3倍 D.4倍
【分析】复印前后的多边形按照比例放大与缩小,因此它们是相似多边形,本题按照相似多边形的性质求解.
【解答】解:由题意可知,相似多边形的边长之比=相似比=1:2,所以面积之比=(1:2)2=1:4.
故选:D.
4.(3分)方程3x2﹣(x﹣1)=0的二次项系数、一次项系数及常数项分别是( )
A.3,,0 B.3,,0 C.3,,﹣1 D.3,,
【分析】先化成一元二次方程的一般形式,再找出二次项系数、一次项系数、常数项即可.
【解答】解:∵3x2﹣(x﹣1)=0,
∴3x2﹣x+=0,
∴方程3x2﹣(x﹣1)=0的二次项系数、一次项系数及常数项分别是3,﹣,,
故选:D.
5.(3分)在△ABC中,若|cosA﹣|+(1﹣tanB)2=0,则∠C的度数是( )
A.45° B.60° C.75° D.105°
【分析】根据非负数的性质可得出cosA及tanB的值,继而可得出A和B的度数,根据三角形的内角和定理可得出∠C的度数.
【解答】解:由题意,得 cosA=,tanB=1,
∴∠A=60°,∠B=45°,
∴∠C=180°﹣∠A﹣∠B=180°﹣60°﹣45°=75°.
故选:C.
6.(3分)如图所示,直线l1∥l2∥l3,下列比例式中错误的是( )
A. B. C. D.
【分析】由平行线分线段成比例的性质,分别对选项进行判断即可.
【解答】解:A.∵l1∥l2∥l3,
∴=,
故A不符合题意;
B..∵l1∥l2∥l3,
∴=,
故A不符合题意;
C.∵l1∥l2∥l3,
∴=,
故C符合题意;
D.∵l1∥l2∥l3,
∴=,
故D不符合题意;
故选:C.
7.(3分)一个公共房门前的台阶高出地面1.2米,台阶拆除后,换成供轮椅行走的斜坡,数据如图所示,则下列关系或结论错误的是( )
A.斜坡AB的坡角是10° B.斜坡AB的坡度是tan10°
C.AC=1.2tan10°米 D.AB=米
【分析】先根据坡度,坡角判断出A,B,再用锐角三角函数判断出C,D即可.
【解答】解:根据坡角的定义得,斜坡AB的坡角是10°,此结论正确;即:A正确,
根据坡度的定义得,斜坡AB的坡度是tan10°,此结论正确;即:B正确,
在Rt△ABC中,∠BAC=10°,BC=1.2,
∴tan∠BAC==,
∴AC=米,此结论错误,即:C错误;
在Rt△ABC中,∠BAC=10°,BC=1.2,
∴sin∠BAC==,
∴AB=米,此结论正确,即:D正确.
故选:C.
8.(3分)如图,△ABC中,点D,E分别在边AB,AC上,下列条件中,不能判定△ABC∽△AED的是( )
A.∠AED=∠B B.∠ADE=∠C C. D.
【分析】根据相似三角形的判定定理对各选项进行逐一判断即可.
【解答】解:A、∠B=∠AED,∠A=∠A,则可判断△ADE∽△ACB,故A选项不符合题意;
B、∠ADE=∠C,∠A=∠A,则可判断△ADE∽△ACB,故B选项不符合题意;
C、=且夹角∠A=∠A,则能判定△ADE∽△ACB,故C选项不符合题意;
D、=,不能确定△ADE∽△ACB,故D选项符合题意.
故选:D.
9.(3分)如图,为测量一棵与地面垂直的树OA的高度,在距离树的底端30米的B处,测得树顶A的仰角∠ABO为α,则树OA的高度为( )
A.米 B.30sinα米 C.30tanα米 D.30cosα米
【分析】根据题意,在Rt△ABO中,BO=30米,∠ABO为α,利用三角函数求解.
【解答】解:在Rt△ABO中,
∵BO=30米,∠ABO为α,
∴AO=BOtanα=30tanα(米).
故选:C.
10.(3分)若关于x的不等式x﹣<1的解集为x<1,则关于x的一元二次方程x2+ax+1=0根的情况是( )
A.有两个相等的实数根 B.有两个不相等的实数根
C.无实数根 D.无法确定
【分析】先解不等式,再利用不等式的解集得到1+=1,则a=0,然后计算判别式的值,最后根据判别式的意义判断方程根的情况.
【解答】解:解不等式x﹣<1得x<1+,
而不等式x﹣<1的解集为x<1,
所以1+=1,解得a=0,
又因为Δ=a2﹣4=﹣4,
所以关于x的一元二次方程x2+ax+1=0没有实数根.
故选:C.
11.(3分)已知m,n是关于x的一元二次方程x2﹣2tx+t2﹣2t+4=0的两实数根,则(m+2)(n+2)的最小值是( )
A.7 B.11 C.12 D.16
【分析】由根与系数的关系可得出m+n=2t、mn=t2﹣2t+4,将其代入(m+2)(n+2)=mn+2(m+n)+4中可得出(m+2)(n+2)=(t+1)2+7,由方程有两个实数根结合根的判别式可求出t的取值范围,再根据二次函数的性质即可得出(m+2)(n+2)的最小值.
【解答】解:∵m,n是关于x的一元二次方程x2﹣2tx+t2﹣2t+4=0的两实数根,
∴m+n=2t,mn=t2﹣2t+4,
∴(m+2)(n+2)=mn+2(m+n)+4=t2+2t+8=(t+1)2+7.
∵方程有两个实数根,
∴Δ=(﹣2t)2﹣4(t2﹣2t+4)=8t﹣16≥0,
∴t≥2,
∴(t+1)2+7≥(2+1)2+7=16.
故选:D.
12.(3分)如图所示,矩形ABCD中,AB=9,BC=6,若矩形AEFG与矩形ABCD位似,位似比为,则C、F之间的距离为( )
A. B.2 C.3 D.12
【分析】连接AF、FC,根据位似变换的性质得到A、F、C在同一条直线上,根据勾股定理求出AC,根据位似比计算即可.
【解答】解:连接AF、FC,
∵矩形AEFG与矩形ABCD位似,
∴A、F、C在同一条直线上,EF∥BC,
∵AB=9,BC=6,
∴AC==3,
∵矩形AEFG与矩形ABCD位似,位似比为,
∴CF=AC=,
故选:A.
二、填空题(每题3分,共24分)
13.(3分)计算:﹣tan45°= 0 .
【分析】根据45°的三角函数值代入计算即可.
【解答】解:原式=﹣1
=1﹣1
=0,
故答案为:0.
14.(3分)已知m是关于x的一元二次方程x2﹣x﹣2=0的一个根,则代数式m2﹣m= 2 .
【分析】将x=m代入原方程即可求m2+m的值.
【解答】解:将x=m代入方程x2﹣x﹣2=0,
得m2﹣m﹣2=0,
即m2﹣m=2,
故答案为:2.
15.(3分)如图,△ABC∽△DEF,∠A=90°,AB=9,AC=DE=6,则DF= 4 .
【分析】利用相似三角形的对应边的比相等列式计算即可.
【解答】解:∵△ABC∽△DEF,
∴AB:DE=AC:DF,
∵AB=9,AC=DE=6,
∴9:6=6:DF,
解得:x=4,
故答案为:4.
16.(3分)如果等腰三角形的底角为30°,底边长为6cm,那么这个三角形的面积为 cm2.
【分析】作底边上的高.运用等腰三角形的性质及三角函数定义分别求三角形的高和底边长,代入公式计算求解.
【解答】解:如图,△ABC,AB=AC,∠B=∠C=30°,BC=cm,作底边BC上的高AD.
∴BD=CD=cm,
∴AD=cm,
∴S△ABC=BC AD=.
故答案为.
17.(3分)如图所示,△ABC的顶点是正方形网格的格点,则sinA的值为 .
【分析】连接CE,求出CE⊥AB,根据勾股定理求出CA,在Rt△AEC中,根据锐角三角函数定义求出即可.
【解答】解:
连接CE,
∵根据图形可知DC=1,AD=3,AC==,
BE=CE==,∠EBC=∠ECB=45°,
∴CE⊥AB,
∴sinA===,
故答案为:.
18.(3分)如图,在矩形ABCD中,AB=4,BC=6,M是边BC的中点,DE⊥AM,垂足为E,则DE= .
【分析】先根据矩形的性质得到AD=BC=6,∠B=90°,AD∥BC,再利用勾股定理计算出AM=5,然后证明△ADE∽△MAB,从而利用相似比计算出DE的长.
【解答】解:∵四边形ABCD为矩形,
∴AD=BC=6,∠B=90°,AD∥BC,
∴∠DAM=∠AMB,
∵M是边BC的中点,
∴BM=BC=3,
在Rt△ABM中,AM===5,
∵DE⊥AM,
∴∠AED=90°,
∵∠DAE=∠AMB,∠AED=∠B,
∴△ADE∽△MAB,
∴=,即=,
∴DE=.
故答案为.
19.(3分)如图,小明同学用自制的直角三角形纸板DEF测量树的高度AB,他调整自己的位置,设法使斜边DF保持水平,并且边DE与点B在同一直线上.已知纸板的两条直角边DE=0.4m,EF=0.2cm,测得边DF离地面的高度AC=1.5m,CD=8m,则树的高度为 5.5 m.
【分析】利用Rt△DEF和Rt△BCD相似求得BC的长后加上边DF到地面的高度CA,即可求得树高AB.
【解答】解:∵∠DEF=∠DCB=90°,∠D=∠D,
∴△DEF∽△DCB
∴=,
∵DE=0.4m,EF=0.2m,CD=8m,
∴=,
∴CB=4(m),
∴AB=AC+BC=1.5+4=5.5(m).
答:树高为5.5m,
故答案为:5.5.
20.(3分)如图,在Rt△ABC中,∠BAC=90°,AB=AC=16cm,AD为BC边上的高.动点P从点A出发,沿A→D方向以cm/s的速度向点D运动.设△ABP的面积为S1,矩形PDFE的面积为S2,运动时间为t秒(0<t<8),则t= 6 秒时,S1=2S2.
【分析】利用三角形的面积公式以及矩形的面积公式,表示出S1和S2,然后根据S1=2S2,即可列方程求解.
【解答】解:∵Rt△ABC中,∠BAC=90°,AB=AC=16cm,AD为BC边上的高,
∴AD=BD=CD=8cm,
又∵AP=t,
则S1=AP BD=×8×t=8t,PD=8﹣t,
∵PE∥BC,
∴△APE∽△ADC,
∴,
∴PE=AP=t,
∴S2=PD PE=(8﹣t) t,
∵S1=2S2,
∴8t=2(8﹣t) t,
解得:t=6.
故答案是:6.
三、解答题(本大题共计60分)
21.(8分)如图,在△ABC中,AB>AC,边AB上取一点D,边AC上取一点E,使AD=AE,直线DE和BC的延长线交于点P.求证:BP:CP=BD:CE.
【分析】如图,过点B作BF∥AC交PD延长线于点F.则△PCE∽△PBF,所以该相似三角形的对应边成比例,即=.根据平行线的性质,等腰三角形的性质以及对顶角的定义得
BF=BD.则=,故BP:CP=BD:CE.
【解答】证明:如图,过点B作BF∥AC交PD延长线于点F.则△PCE∽△PBF,
∴=.
∵BF∥AC,
∴∠1=∠2.
又∵AD=AE,
∴∠2=∠4,
∠1=∠3=∠4,
∴BF=BD.
∴=,
∴BP:CP=BD:CE.
22.(9分)已知关于x的一元二次方程x2﹣(2m+3)x+m2+2=0.
(1)若方程有实数根,求实数m的取值范围;
(2)若方程两实数根分别为x1、x2,且满足x12+x22=31+|x1x2|,求实数m的值.
【分析】(1)利用判别式的意义得到(2m+3)2﹣4(m2+2)≥0,然后解不等式即可;
(2)根据题意x1+x2=2m+3,x1x2=m2+2,由条件得x12+x22=31+x1x2,再利用完全平方公式得(x1+x2)2﹣3x1x2﹣31=0,所以2m+3)2﹣3(m2+2)﹣31=0,然后解关于m的方程,最后利用m的范围确定满足条件的m的值.
【解答】解:(1)根据题意得(2m+3)2﹣4(m2+2)≥0,
解得m≥﹣;
(2)根据题意x1+x2=2m+3,x1x2=m2+2,
因为x1x2=m2+2>0,
所以x12+x22=31+x1x2,
即(x1+x2)2﹣3x1x2﹣31=0,
所以(2m+3)2﹣3(m2+2)﹣31=0,
整理得m2+12m﹣28=0,解得m1=﹣14,m2=2,
而m≥﹣;
所以m=2.
23.(9分)如图,在等腰Rt△ABC中,∠C=90°,AC=6,D为AC上一点,且tan∠DBA=,求AD的长度.
【分析】过点D作DH⊥AB于点H,根据等腰直角三角形的性质,勾股定理以及锐角三角形函数的定义即可求出答案.
【解答】解:过点D作DH⊥AB于点H,
∵等腰三角形ABC,∠C=90°,
∴∠A=45°,
∴AH=DH,
设AH=x,
∴DH=x,
∵tan∠DBA=,
∴BH=5x,
∴AB=6x,
∵AC=6,
∴由勾股定理可知:AB=6,
∴x=,
∴AH=DH=,
∴由勾股定理可知:AD=2.
24.(10分)列方程解应用题:
某玩具厂生产一种玩具,按照控制固定成本降价促销的原则,使生产的玩具能够及时售出,据市场调查:每个玩具按480元销售时,每天可销售160个;若销售单价每降低1元,每天可多售出2个.已知每个玩具的固定成本为360元,问这种玩具的销售单价为多少元时,厂家每天可获利润20000元?
【分析】根据单件利润×销售量=总利润,列方程求解即可.
【解答】解:设销售单价为x元,
由题意,得:(x﹣360)[160+2(480﹣x)]=20000,
整理,得:x2﹣920x+211600=0,
解得:x1=x2=460,
答:这种玩具的销售单价为460元时,厂家每天可获利润20000元.
25.(11分)如图,在△ABC中,AD是∠BAC的平分线,AD的垂直平分线EF交CB的延长线于点F,交AD于点E,交AC于点M.
(1)△ACF与△BAF相似吗?请说明理由;
(2)如果AF=6,BD=2,AC=4,求DC和AM的长.
【分析】(1)首先证明∠DAF=∠ADF,结合平分线的性质以及角角之间的数量关系得到∠BAF=∠C,再根据∠AFB=∠AFC即可判定△ACF与△BAF相似;
(2)连接DM,首先求出BF的长度,利用△ACF与△BAF相似,得到,结合题干数据求出CF的长度,进而求出CD的长度,由∠DAM=∠ADM,∠BAD=∠CAD,得到∠BAD=∠ADM,进而得到DM∥BA,即,结合线段之间的数量关系即求出AM的长.
【解答】解:(1)△ACF∽△BAF.
∵EF垂直平分AD,
∴AF=DF,
∴∠DAF=∠ADF.
∵AD平分∠BAC,
∴∠BAD=∠CAD,
∵∠DAF=∠BAF+∠BAD,∠ADF=∠C+∠CAD,
∴∠BAF=∠C.
又∵∠AFB=∠AFC,
∴△ACF∽△BAF.
(2)连接DM.
∵EF垂直平分AD,
∴DM=AM,DF=AF=6.
∵BD=2.
∴BF=6﹣2=4.
由(1)知,△ACF∽△BAF,
∴.
∴AF2=BF CF,即36=4CF.解得CF=9.
∴CD=CF﹣FD=9﹣6=3.
∵∠DAM=∠ADM,∠BAD=∠CAD,
∴∠BAD=∠ADM.
∴DM∥BA.
∴.
∴.
∵BC=DC+BD=3+2=5.
即.
∴AM=.
26.(13分)如图,港口B位于港口O正西方向120海里处,小岛C位于港口O北偏西60°的方向.一艘科学考察船从港口O出发,沿北偏西30°的OA方向以20海里/小时的速度驶离港口O.同时一艘快艇从港口B出发,沿北偏东30°的方向以60海里/小时的速度驶向小岛C,在小岛C用1小时装补给物资后,立即按原来的速度给考察船送去.
(1)快艇从港口B到小岛C需要多少时间?
(2)快艇从小岛C出发后最少需要多少时间才能和考察船相遇?
【分析】(1)要求B到C的时间,已知其速度,则只要求得BC的路程,再利用路程公式即可求得所需的时间.
(2)过C作CH⊥OA,垂足为H.设快艇从C岛出发后最少要经过x小时才能和考察船在OA上的D处相遇,则CD=60x,OD=20(x+2).根据直角三角形的性质可解得x的值,从而求得快艇从小岛C出发后和考察船相遇的最短的时间.
【解答】解:(1)由题意可知:∠CBO=60°,∠COB=30度.
∴∠BCO=90度.
在Rt△BCO中,
∵OB=120,
∴BC=60,OC=60.
∴快艇从港口B到小岛C的时间为:60÷60=1(小时).
(2)设快艇从C岛出发后最少要经过x小时才能和考察船在
OA上的D处相遇,则CD=60x.
过点D作DE⊥CO于点E,
∵考察船与快艇是同时出发,
∵快艇从港口B到小岛C的时间是1小时,在小岛C用1小时装补给物资,
∴考察船从O到D行驶了(x+2)小时,
∴OD=20(x+2).
过C作CH⊥OA,垂足为H,
在△OHC中,
∵∠COH=30°,OB=120,
∴CO=60,
∴CH=30,OH=90.
∴DH=OH﹣OD=90﹣20(x+2)=50﹣20x.
在Rt△CHD中,CH2+DH2=CD2,
∴+(50﹣20x)2=(60x)2.
整理得:8x2+5x﹣13=0.
解得:x1=1,x2=﹣.
∵x>0,
∴x=1.
答:快艇从小岛C出发后最少需要1小时才能和考察船相遇.
同课章节目录
