2021-2022学年安徽省六安市金安区汇文中学九年级(上)第一次月考数学试卷(Word版 含解析)
文档属性
| 名称 | 2021-2022学年安徽省六安市金安区汇文中学九年级(上)第一次月考数学试卷(Word版 含解析) |  | |
| 格式 | doc | ||
| 文件大小 | 623.6KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 沪科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-10-20 07:33:48 | ||
图片预览



文档简介
2021-2022学年安徽省六安市金安区汇文中学九年级(上)第一次月考数学试卷
一、单选题(每题4分,共计40分)
1.(4分)抛物线y=2(x﹣1)2+6的顶点坐标是( )
A.(2,6) B.(1,6) C.(2,1) D.(﹣1,6)
2.(4分)校园里一片小小的树叶,也蕴含着“黄金分割”,如图,P为AB的黄金分割点(AP>PB),如果AB的长度为10cm,那么AP的长度为( )cm.
A.﹣1 B.2﹣2 C.5﹣5 D.10﹣10
3.(4分)将抛物线y=x2﹣4x+8向上平移1个单位长度,再向左平移3个单位长度后,得到的抛物线解析式是( )
A.y=(x+1)2+5 B.y=(x+1)2+3 C.y=(x﹣5)2+5 D.y=(x﹣5)2+3
4.(4分)若点A(﹣5,y1),B(1,y2),C(5,y3)都在反比例函数y=﹣的图象上,则y1,y2,y3的大小关系是( )
A.y1<y2<y3 B.y2<y3<y1 C.y1<y3<y2 D.y3<y1<y2
5.(4分)如图,直线l1∥l2∥l3,直线AC分别交l1,l2,l3于点A,B,C,直线DF分别交l1,l2,l3于点D,E,F,AC与DF相交于点H,如果AB=5,BH=1,CH=2,那么的值等于( )
A. B. C. D.
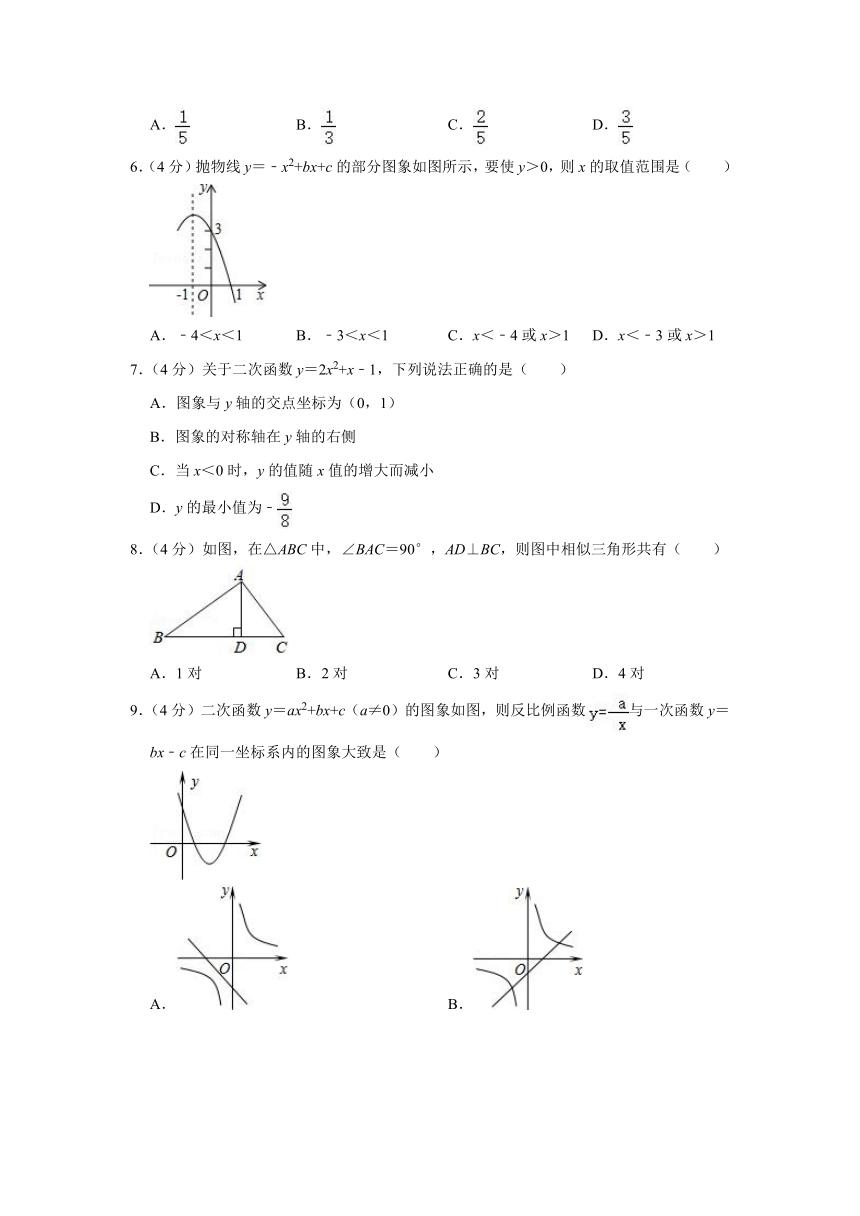
6.(4分)抛物线y=﹣x2+bx+c的部分图象如图所示,要使y>0,则x的取值范围是( )
A.﹣4<x<1 B.﹣3<x<1 C.x<﹣4或x>1 D.x<﹣3或x>1
7.(4分)关于二次函数y=2x2+x﹣1,下列说法正确的是( )
A.图象与y轴的交点坐标为(0,1)
B.图象的对称轴在y轴的右侧
C.当x<0时,y的值随x值的增大而减小
D.y的最小值为﹣
8.(4分)如图,在△ABC中,∠BAC=90°,AD⊥BC,则图中相似三角形共有( )
A.1对 B.2对 C.3对 D.4对
9.(4分)二次函数y=ax2+bx+c(a≠0)的图象如图,则反比例函数与一次函数y=bx﹣c在同一坐标系内的图象大致是( )
A. B.
C. D.
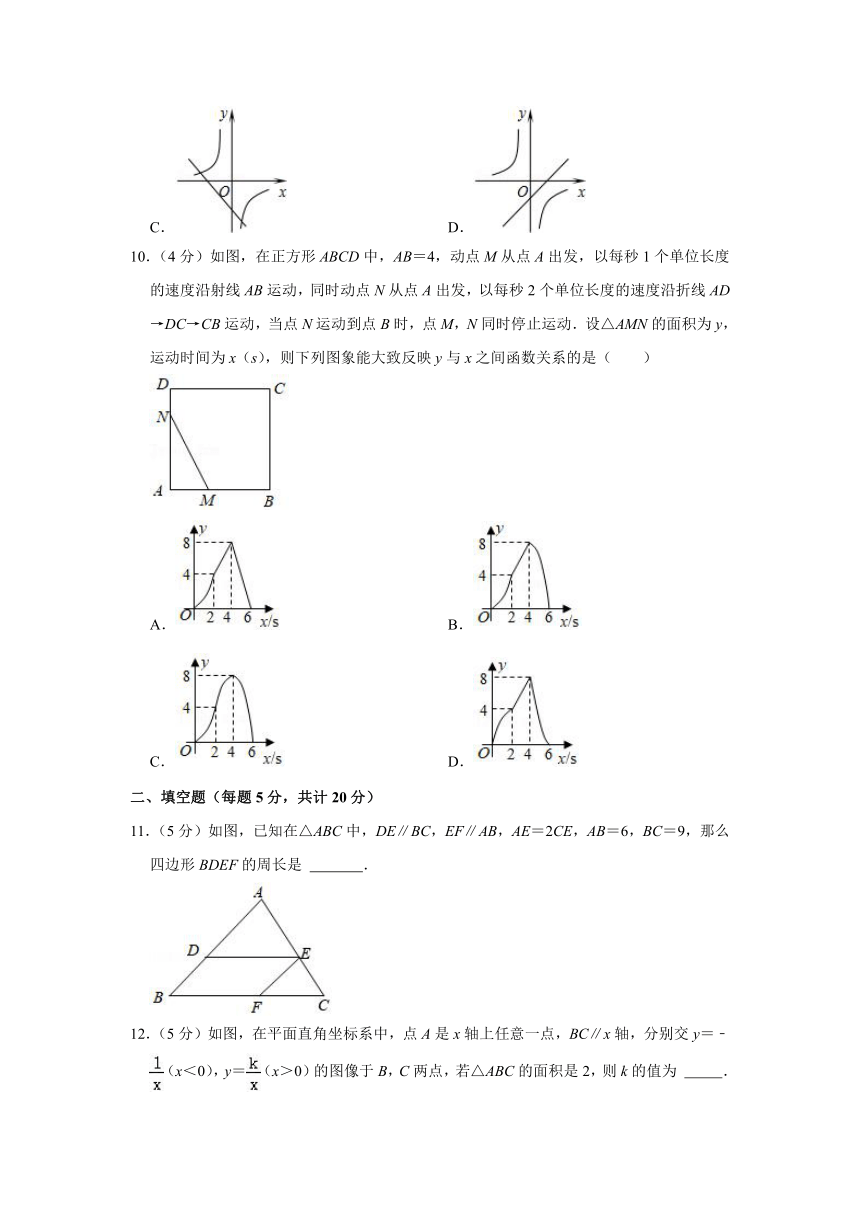
10.(4分)如图,在正方形ABCD中,AB=4,动点M从点A出发,以每秒1个单位长度的速度沿射线AB运动,同时动点N从点A出发,以每秒2个单位长度的速度沿折线AD→DC→CB运动,当点N运动到点B时,点M,N同时停止运动.设△AMN的面积为y,运动时间为x(s),则下列图象能大致反映y与x之间函数关系的是( )
A. B.
C. D.
二、填空题(每题5分,共计20分)
11.(5分)如图,已知在△ABC中,DE∥BC,EF∥AB,AE=2CE,AB=6,BC=9,那么四边形BDEF的周长是 .
12.(5分)如图,在平面直角坐标系中,点A是x轴上任意一点,BC∥x轴,分别交y=﹣(x<0),y=(x>0)的图像于B,C两点,若△ABC的面积是2,则k的值为 .
13.(5分)在△ABC和△DEF中,∠A=∠D=105°,AC=4cm,AB=6cm,DE=3cm,则DF= 时,△ABC与△DEF相似.
14.(5分)在直角坐标系中,点A的坐标为(3,0),若抛物线y=x2﹣2x+n﹣1与线段OA有且只有一个公共点,则n的取值范围为 .
三、解答题
15.(8分)已知线段a,b,c,且.
(1)求的值.
(2)若线段a+b+c=45,求a﹣b+c的值.
16.(8分)已知函数y=y1+y2,y1与x成正比例,y2与x成反比例,且当x=1时,y=4;当x=2时,y=5.
(1)求y与x的函数关系式;
(2)当x=4时,求y的值.
17.(8分)如图,已知反比例函数y1=的图象与一次函数y2=x+b的图象交于点A(1,4),点B(﹣4,n).
(1)求反比例函数和一次函数的表达式;
(2)求△OAB的面积;
(3)直接写出y2>y1时自变量x的取值范围.
18.(8分)已知:如图,△ABC中,∠BAC=90°,AB=AC=1,点D是BC边上的一个动点(不与B,C点重合),∠ADE=45°.求证:△ABD∽△DCE.
19.(10分)如图,点P(x,y1)与Q(x,y2)分别是两个函数图象C1与C2上的任一点.当a≤x≤b时,有﹣1≤y1﹣y2≤1成立,则称这两个函数在a≤x≤b上是“相邻函数”,否则称它们在a≤x≤b上是“非相邻函数”.例如,点P(x,y1)与Q (x,y2)分别是两个函数y=3x+1与y=2x﹣1图象上的任一点,当﹣3≤x≤﹣1时,y1﹣y2=(3x+1)﹣(2x﹣1)=x+2,通过构造函数y=x+2并研究它在﹣3≤x≤﹣1上的性质,得到该函数值的范围是﹣1≤y≤1,所以﹣1≤y1﹣y2≤1成立,因此这两个函数在﹣3≤x≤﹣1上是“相邻函数”.
(1)判断函数y=3x+1与y=2x+2在0≤x≤2上是否为“相邻函数”,并说明理由;
(2)若函数y=x2﹣x与y=x a在0≤x≤2上是“相邻函数”,求a的取值范围.
20.(10分)已知抛物线y=ax2+bx﹣3(a≠0)的对称轴为直线x=1,且抛物线经过点A(﹣1,0),它与x轴的另一交点为B,与y轴的交点为C.
(1)求这条抛物线所对应的函数表达式;
(2)在直线x=1上求点M,使△AMC的周长最小,并求△AMC的周长.
21.(12分)某社区决定把一块长50m,宽30m的矩形空地建成居民健身广场,设计方案如图,阴影区域为绿化区(四块绿化区为大小、形状都相同的矩形),空白区域为活动区,且四周的4个出口宽度相同,其宽度不小于14m,不大于26m,设绿化区较长边为xm,活动区的面积为ym2.为了想知道出口宽度的取值范围,小明同学根据出口宽度不小于14m,算出x≤18.
(1)求y与x的函数关系式并直接写出自变量x的取值范围;
(2)求活动区的最大面积;
(3)预计活动区造价为50元/m2,绿化区造价为40元/m2,若社区的此项建造投资费用不得超过72000元,求投资费用最少时活动区的出口宽度?
22.(12分)如图,Rt△ABC中,∠ACB=90°,∠B=60°,BC=2cm,D为BC的中点,若动点E以1cm/s的速度从A点出发,沿着A→B的方向运动,设E点的运动时间为t秒(0≤t<4),连接DE,当t为何值时,以B、E、D为顶点的三角形与△ABC相似?
23.(14分)如图1,在平面直角坐标系中,二次函数y=﹣x2+bx+c的图像与x轴交于点A(﹣1,0),B(3,0),与y轴交于C.
(1)求该二次函数的表达式;
(2)二次函数位于x轴上方的图像上是否存在点P,使得S△BOP=3S△AOC?如果存在,请求出点P的坐标;若不存在,请说明理由;
(3)如图2,点D为线段BC上的一个动点,过点D作DE∥y轴,交二次函数的图像于点E,求线段DE长度的最大值.
2021-2022学年安徽省六安市金安区汇文中学九年级(上)第一次月考数学试卷
参考答案与试题解析
一、单选题(每题4分,共计40分)
1.(4分)抛物线y=2(x﹣1)2+6的顶点坐标是( )
A.(2,6) B.(1,6) C.(2,1) D.(﹣1,6)
【分析】根据y=a(x﹣h)2+k,顶点坐标是(h,k),可得答案.
【解答】解:∵抛物线为y=2(x﹣1)2+6,
∴顶点坐标(1,6).
故选:B.
2.(4分)校园里一片小小的树叶,也蕴含着“黄金分割”,如图,P为AB的黄金分割点(AP>PB),如果AB的长度为10cm,那么AP的长度为( )cm.
A.﹣1 B.2﹣2 C.5﹣5 D.10﹣10
【分析】直接利用黄金分割的定义计算出AP的长即可.
【解答】解:∵P为AB的黄金分割点(AP>PB),AB=10cm,
∴AP=AB=×10=5﹣5(cm),
故选:C.
3.(4分)将抛物线y=x2﹣4x+8向上平移1个单位长度,再向左平移3个单位长度后,得到的抛物线解析式是( )
A.y=(x+1)2+5 B.y=(x+1)2+3 C.y=(x﹣5)2+5 D.y=(x﹣5)2+3
【分析】根据“上加下减,左加右减”的法则解答.
【解答】解:将抛物线y=x2﹣4x+8=(x﹣2)2+4向上平移1个单位长度,再向左平移3个单位长度后所得新抛物线的表达式为y=(x﹣2+3)2+4+1,
即y=(x+1)2+5.
故选:A.
4.(4分)若点A(﹣5,y1),B(1,y2),C(5,y3)都在反比例函数y=﹣的图象上,则y1,y2,y3的大小关系是( )
A.y1<y2<y3 B.y2<y3<y1 C.y1<y3<y2 D.y3<y1<y2
【分析】先根据反比例函数的解析式判断出函数图象所在的象限及其增减性,再由各点横坐标的值即可得出结论.
【解答】解:∵反比例函数y=﹣中,k=﹣5<0,
∴函数图象的两个分支分别位于二四象限,且在每一象限内,y随x的增大而增大.
∵﹣5<0,0<1<5,
∴点A(﹣5,y1)在第二象限,点B(1,y2),C(5,y3)在第四象限,
∴y2<y3<y1.
故选:B.
5.(4分)如图,直线l1∥l2∥l3,直线AC分别交l1,l2,l3于点A,B,C,直线DF分别交l1,l2,l3于点D,E,F,AC与DF相交于点H,如果AB=5,BH=1,CH=2,那么的值等于( )
A. B. C. D.
【分析】根据平行线分线段成比例,可以解答本题.
【解答】解:∵直线l1∥l2∥l3,
∴=,
∵AB=5,BH=1,CH=2,
∴BC=BH+CH=3,
∴=,
∴=.
故选:D.
6.(4分)抛物线y=﹣x2+bx+c的部分图象如图所示,要使y>0,则x的取值范围是( )
A.﹣4<x<1 B.﹣3<x<1 C.x<﹣4或x>1 D.x<﹣3或x>1
【分析】根据抛物线的对称性可知,图象与x轴的另一个交点是﹣3,y>0反映到图象上是指x轴上方的部分,对应的x值即为x的取值范围.
【解答】解:∵抛物线与x轴的一个交点是(1,0),对称轴是直线x=﹣1,
根据抛物线的对称性可知,抛物线与x轴的另一交点是(﹣3,0),
又图象开口向下,
∴当﹣3<x<1时,y>0.
故选:B.
7.(4分)关于二次函数y=2x2+x﹣1,下列说法正确的是( )
A.图象与y轴的交点坐标为(0,1)
B.图象的对称轴在y轴的右侧
C.当x<0时,y的值随x值的增大而减小
D.y的最小值为﹣
【分析】根据二次函数的性质和二次函数的最值即可求解.
【解答】解:A.图象与y轴的交点坐标为(0,﹣1),故A选项不符合题意;
B.图象的对称轴是直线x=在y轴的左侧,故B选项不符合题意;
C.当x时,y的值随x值的增大而减小,当x时,y的值随x值的增大而增大,故C选项不符合题意;
D.∵y=2x2+x﹣1=2(x+)2﹣,
∴当x=﹣时,y取最小值,y的最小值为﹣,故D选项符合题意;
故选:D.
8.(4分)如图,在△ABC中,∠BAC=90°,AD⊥BC,则图中相似三角形共有( )
A.1对 B.2对 C.3对 D.4对
【分析】利用直角三角形的性质和相似三角形的判定方法,可得结论.
【解答】解:∵AD⊥BC,
∴∠ADC=90°,
∵∠BAC=90°,
∴∠ADC=∠BAC,
又∵∠B=∠B,
∴△BAD∽△BCA,
∵∠ADC=∠BAC,∠C=∠C,
∴△CAD∽△CBA,
∴△BAD∽△ACD,
∴共有3对,
故选:C.
9.(4分)二次函数y=ax2+bx+c(a≠0)的图象如图,则反比例函数与一次函数y=bx﹣c在同一坐标系内的图象大致是( )
A. B.
C. D.
【分析】根据二次函数的图象找出a、b、c的正负,再结合反比例函数、一次函数系数与图象的关系即可得出结论.
【解答】解:观察二次函数图象可知:
开口向上,a>0;对称轴大于0,﹣>0,b<0;二次函数图象与y轴交点在y轴的正半轴,c>0.
∵反比例函数中k=﹣a<0,
∴反比例函数图象在第二、四象限内;
∵一次函数y=bx﹣c中,b<0,﹣c<0,
∴一次函数图象经过第二、三、四象限.
故选:C.
10.(4分)如图,在正方形ABCD中,AB=4,动点M从点A出发,以每秒1个单位长度的速度沿射线AB运动,同时动点N从点A出发,以每秒2个单位长度的速度沿折线AD→DC→CB运动,当点N运动到点B时,点M,N同时停止运动.设△AMN的面积为y,运动时间为x(s),则下列图象能大致反映y与x之间函数关系的是( )
A. B.
C. D.
【分析】根据点N的运动情况,分点N在AD,DC,CB上三种情况讨论,分别写出每种情况y和x之间的函数关系式,即可确定图象.
【解答】解:当点N在AD上时,即0<x<2
∵AM=x,AN=2x,
∴,
此时二次项系数大于0,
∴该部分函数图象开口向上,
当点N在DC上时,即2≤x<4,
此时底边AM=x,高AD=4,
∴y==2x,
∴该部分图象为直线段,
当点N在CB上时,即4≤x<6时,
此时底边AM=x,高BN=12﹣2x,
∴y=,
∵﹣1<0,
∴该部分函数图象开口向下,
故选:B.
二、填空题(每题5分,共计20分)
11.(5分)如图,已知在△ABC中,DE∥BC,EF∥AB,AE=2CE,AB=6,BC=9,那么四边形BDEF的周长是 16 .
【分析】由平行线分线段成比例得出比例式,然后证明四边形BDEF是平行四边形,得出对应边相等,即可得出结果.
【解答】解:∵AE=2CE,
∴,
∵EF∥AB
∴,
∵BC=9,
∴BF=6,
∵DE∥BC
∴,
∵AB=6,
∴BD=2;
∵EF∥AB,DE∥BC
∴四边形BDEF是平行四边形,
∴BD=EF=2,DE=BF=6,
∴四边形BDEF的周长2(2+6)=16,
故答案为:16.
12.(5分)如图,在平面直角坐标系中,点A是x轴上任意一点,BC∥x轴,分别交y=﹣(x<0),y=(x>0)的图像于B,C两点,若△ABC的面积是2,则k的值为 3 .
【分析】连接OC、OB,如图,由于BC∥x轴,根据三角形面积公式得到S△ACB=S△OCB,再利用反比例函数系数k的几何意义得到 |﹣1|+ |k|=2,然后解关于k的绝对值方程可得到满足条件的k的值.
【解答】解:连接OC、OB,如图,
∵BC∥x轴,
∴S△ACB=S△OCB,
而S△OCB= |﹣1|+ |k|,
∴ |﹣1|+ |k|=2,
而k>0,
∴k=3.
故答案为:3.
13.(5分)在△ABC和△DEF中,∠A=∠D=105°,AC=4cm,AB=6cm,DE=3cm,则DF= 2cm或4.5cm 时,△ABC与△DEF相似.
【分析】由于两相似三角形的对应边不能确定,故应分△ABC∽△DEF与△ABC∽△DFE两种情况进行讨论.
【解答】解:∵∠A=∠D,AB=6cm,AC=4cm,DE=3cm,
∴当△ABC∽△DEF时,=,即=,
解得:DF=2;
当△ABC∽△DFE时,=,
即=,
解得:DF=4.5.
综上所述,当DF=2cm或4.5cm时,△ABC和△DEF相似.
故答案为:2cm或4.5cm.
14.(5分)在直角坐标系中,点A的坐标为(3,0),若抛物线y=x2﹣2x+n﹣1与线段OA有且只有一个公共点,则n的取值范围为 ﹣2≤n<1或n=2 .
【分析】根据题意可以将函数解析式化为顶点式,由抛物线y=x2﹣2x+n﹣1与线段OA有且只有一个公共点,可以得到顶点的纵坐标为0或当x=0时y<0且当x=3时,y不小于0,从而可以求得x的取值范围.
【解答】解:∵点A的坐标为(3,0),抛物线y=x2﹣2x+n﹣1=(x﹣1)2+n﹣2与线段OA有且只有一个公共点,
∴n﹣2=0或,
解得,﹣2≤n<1或n=2,
故答案为:﹣2≤n<1或n=2.
三、解答题
15.(8分)已知线段a,b,c,且.
(1)求的值.
(2)若线段a+b+c=45,求a﹣b+c的值.
【分析】(1)根据比例的性质得出,即可得出的值;
(2)首先设,则a=4k,b=5k,c=6k,利用a+b+c=45求出k的值即可得出答案.
【解答】解:,
∴,
∴;
( 2 ) 设,则a=4k,b=5k,c=6k,
∵a+b+c=45,
∴4k+5k+6k=45,
∴k=3,
∴a=12,b=15,c=18,
∴a﹣b+c=12﹣15+18=15.
16.(8分)已知函数y=y1+y2,y1与x成正比例,y2与x成反比例,且当x=1时,y=4;当x=2时,y=5.
(1)求y与x的函数关系式;
(2)当x=4时,求y的值.
【分析】首先根据正比例与反比例函数的定义分别设出函数解析式,用待定系数法求出y与x的函数关系式,然后再代入求值.
【解答】解:设y1=k1x,y2=,则y=k1x+;
将x=1,y=4;x=2,y=5分别代入得:,
解得:k1=2,k2=2;
则y与x的函数关系式:y=2x+;
(2)把x=4代入y=2x+,
得:y=2×4+=8.
17.(8分)如图,已知反比例函数y1=的图象与一次函数y2=x+b的图象交于点A(1,4),点B(﹣4,n).
(1)求反比例函数和一次函数的表达式;
(2)求△OAB的面积;
(3)直接写出y2>y1时自变量x的取值范围.
【分析】(1)把点A坐标代入反比例函数求出m的值,也就求出了反比例函数解析式,再把点B的坐标代入反比例函数解析式求出n的值,得到点B的坐标,然后利用待定系数法即可求出一次函数解析式;
(2)先求出直线与x轴的交点坐标,从而x轴把△AOB分成两个三角形,结合点A、B的纵坐标分别求出两个三角形的面积,相加即可;
(3)根据函数的图象求得即可.
【解答】解:(1)点A(1,4)在反比例函数y1=的图象上,
∴k=1×4=4,
∴反比例函数的表达式为y1=,
∵点B(﹣4,n)也在反比例函数y1=的图象上,
∴n==﹣1,
即B(﹣4,﹣1),
把点A(1,4),点B(﹣4,﹣1)代入一次函数y2=kx+b中,,解得,
∴一次函数的表达式为y2=x+3;
故反比例函数解析式为y1=,一次函数得到解析式为y2=x+3;
(2)设直线与x轴的交点为C,
在y2=x+3中,当y=0时,得x=﹣3,
∴直线y2=x+3与x轴的交点为C(﹣3,0),
∵线段OC将△AOB分成△AOC和△BOC,
∴S△AOB=S△AOC+S△BOC=×3×4+×3×1=7.5;
(3)从图象看,当﹣4<x<0或x>1时,y2>y1.
18.(8分)已知:如图,△ABC中,∠BAC=90°,AB=AC=1,点D是BC边上的一个动点(不与B,C点重合),∠ADE=45°.求证:△ABD∽△DCE.
【分析】先判断△ABC为等腰直角三角形得到∠B=∠C=45°,再利用三角形内角和得到∠1+∠2=135°,利用平角定义得到∠2++∠3=135°,则∠1=∠3,于是可根据有两组角对应相等的两个三角形相似得到结论.
【解答】证明:∵∠BAC=90°,AB=AC=1,
∴△ABC为等腰直角三角形,
∴∠B=∠C=45°,
∴∠1+∠2=180°﹣∠B=135°,
∵∠ADE=45°,
∴∠2+∠3=135°,
∴∠1=∠3,
∵∠B=∠C,
∴△ABD∽△DCE.
19.(10分)如图,点P(x,y1)与Q(x,y2)分别是两个函数图象C1与C2上的任一点.当a≤x≤b时,有﹣1≤y1﹣y2≤1成立,则称这两个函数在a≤x≤b上是“相邻函数”,否则称它们在a≤x≤b上是“非相邻函数”.例如,点P(x,y1)与Q (x,y2)分别是两个函数y=3x+1与y=2x﹣1图象上的任一点,当﹣3≤x≤﹣1时,y1﹣y2=(3x+1)﹣(2x﹣1)=x+2,通过构造函数y=x+2并研究它在﹣3≤x≤﹣1上的性质,得到该函数值的范围是﹣1≤y≤1,所以﹣1≤y1﹣y2≤1成立,因此这两个函数在﹣3≤x≤﹣1上是“相邻函数”.
(1)判断函数y=3x+1与y=2x+2在0≤x≤2上是否为“相邻函数”,并说明理由;
(2)若函数y=x2﹣x与y=x a在0≤x≤2上是“相邻函数”,求a的取值范围.
【分析】(1)通过构建函数y=x﹣1,根据一次函数的性质可得出该函数在0≤x≤2上单调递增,分别代入x=0、x=2即可得出y的取值范围,由此即可得出结论;
(2)由函数y=x2﹣x与y=x a在0≤x≤2上是“相邻函数”,构造函数y=x2﹣(a+1)x,根据抛物线的位置不同,令其最大值≤1、最小值≥﹣1,解关于a的不等式组即可得出结论.
【解答】解:(1)函数y=3x+1与y=2x+2在0≤x≤2上是“相邻函数”,理由如下:
点P(x,y1)与Q (x,y2)分别是两个函数y=3x+1与y=2x+2图象上的任一点,
当0≤x≤2时,y1﹣y2=(3x+1)﹣(2x+2)=x﹣1,
通过构造函数y=x﹣1并研究它在0≤x≤2上的性质,得到该函数值的范围是﹣1≤y≤1,
所以﹣1≤y1﹣y2≤1成立,
因此这两个函数在0≤x≤2上是“相邻函数”.
(2)∵函数y=x2﹣x与y=x a在0≤x≤2上是“相邻函数”,
∴构造函数y=x2﹣(a+1)x,在0≤x≤2上﹣1≤y≤1.
根据抛物线y=x2﹣(a+1)x对称轴的位置不同,来考虑:
①当≤0,即a≤﹣1时(图1),
,解得:a≥,
∴此时无解;
②当0<≤1,即﹣1<a≤1时(图2),
,解得:≤a≤1,
∴≤a≤1;
③当1<≤2,即1<a≤3时(图3),
,解得:﹣3≤a≤1,
∴此时无解;
④当2<,即a>3时(图4),
,解得:a≤,
∴此时无解.
综上可知:若函数y=x2﹣x与y=x a在0≤x≤2上是“相邻函数”,则a的取值范围为≤a≤1.
20.(10分)已知抛物线y=ax2+bx﹣3(a≠0)的对称轴为直线x=1,且抛物线经过点A(﹣1,0),它与x轴的另一交点为B,与y轴的交点为C.
(1)求这条抛物线所对应的函数表达式;
(2)在直线x=1上求点M,使△AMC的周长最小,并求△AMC的周长.
【分析】(1)由抛物线的对称轴求出B(3,0),将A,B两点的坐标代入抛物线的解析式可得出关于a,b的方程组,解方程组可得出答案.
(2)直线BC与对称轴直线x=1的交点即为所求使△PAC的周长最小的点M的坐标.
【解答】解:(1)∵A(﹣1,0),
∴点A关于直线x=1的对称点是点B(3,0),
∴,
解得,
∴抛物线所对应的函数表达式为y=x2﹣2x﹣3;
(2)∵抛物线y=x2﹣2x﹣3与y轴的交点为C.
∴C(0,﹣3)
连接BC,交对称轴于点M,则此时△AMC周长最小,
设直线BC的关系式为:y=mx+n,
把B(3,0),C(0,﹣3)代入y=mx+n得,
,
解得.
∴直线BC的关系式为y=x﹣3,
当x=1时,y=1﹣3=﹣2,
∴M点坐标为(1,﹣2);
∵BC===3,AC==,
∴△AMC的周长=3+;
21.(12分)某社区决定把一块长50m,宽30m的矩形空地建成居民健身广场,设计方案如图,阴影区域为绿化区(四块绿化区为大小、形状都相同的矩形),空白区域为活动区,且四周的4个出口宽度相同,其宽度不小于14m,不大于26m,设绿化区较长边为xm,活动区的面积为ym2.为了想知道出口宽度的取值范围,小明同学根据出口宽度不小于14m,算出x≤18.
(1)求y与x的函数关系式并直接写出自变量x的取值范围;
(2)求活动区的最大面积;
(3)预计活动区造价为50元/m2,绿化区造价为40元/m2,若社区的此项建造投资费用不得超过72000元,求投资费用最少时活动区的出口宽度?
【分析】(1)根据“活动区的面积=矩形空地面积﹣阴影区域面积”列出函数解析式便可,图形可得结论;
(2)根据题意可得y与x的关系式;
(3)根据二次函数的增减性及解一元二次方程可得结论;
【解答】解:(1)根据题意,绿化区的宽为:[30﹣(50﹣2x)]÷2=x﹣10
∴y=50×30﹣4x(x﹣10)=﹣4x2+40x+1500,
∵4个出口宽度相同,其宽度不小于14m,不大于26m,
∴12≤x≤18,
∴y=﹣4x2+40x+1500(12≤x≤18);
(2)y=﹣4x2+40x+1500=﹣4(x﹣5)2+1600,
∵a=﹣4<0,抛物线的开口向下,当12≤x≤18时,y随x的增大而减小,
∴当x=12时,y最大=1404,
答:活动区的最大面积为1404m2.
(3)设投资费用为w元,
由题意得,w=50(﹣4x2+40x+1500)+40×4x(x﹣10)=﹣40(x﹣5)2+76000,
∴当w=72000时,解得:x1=﹣5(不符合题意舍去),x2=15,
∵a=﹣40<0,
∴当x≥15时,w≤72000,
又∵12≤x≤18,
∴15≤x≤18,
∴当x=18时,投资费用最少,此时出口宽度为50﹣2x=50﹣2×18=14(m),
答:投资最少时活动区的出口宽度为14m.
22.(12分)如图,Rt△ABC中,∠ACB=90°,∠B=60°,BC=2cm,D为BC的中点,若动点E以1cm/s的速度从A点出发,沿着A→B的方向运动,设E点的运动时间为t秒(0≤t<4),连接DE,当t为何值时,以B、E、D为顶点的三角形与△ABC相似?
【分析】求出AB=2BC=4cm,分两种情况:①当∠EDB=∠ACB=90°时,DE∥AC,△EBD∽△ABC,得出AE=BE=AB=2cm,即可得出t=2s;②当∠DEB=∠ACB=90°时,证出△DBE∽△ABC,得出∠BDE=∠A=30°,因此BE=BD=cm,得出AE=3.5cm,t=3.5s;即可得出结果.
【解答】解:∵∠ACB=90°,∠ABC=60°,
∴∠A=30°,
∴AB=2BC=4cm,
分两种情况:
①当∠EDB=∠ACB=90°时,
DE∥AC,△EBD∽△ABC,
∵D为BC的中点,
∴BD=CD=BC=1cm,E为AB的中点,AE=BE=AB=2cm,
∴t=2s;
②当∠DEB=∠ACB=90°时,
∵∠B=∠B,
∴△DBE∽△ABC,
∴∠BDE=∠A=30°,
∴BE=BD=cm,
∴AE=3.5cm,
∴t=3.5s;
综上所述:当以B、D、E为顶点的三角形与△ABC相似时,t的值为2或3.5;
23.(14分)如图1,在平面直角坐标系中,二次函数y=﹣x2+bx+c的图像与x轴交于点A(﹣1,0),B(3,0),与y轴交于C.
(1)求该二次函数的表达式;
(2)二次函数位于x轴上方的图像上是否存在点P,使得S△BOP=3S△AOC?如果存在,请求出点P的坐标;若不存在,请说明理由;
(3)如图2,点D为线段BC上的一个动点,过点D作DE∥y轴,交二次函数的图像于点E,求线段DE长度的最大值.
【分析】(1)将点A和点B的坐标代入函数解析式得到关于b和c的方程组,然后求得b和c的大小,最后得到解析式;
(2)先求出点C的坐标,结合点A求得△AOC的面积,然后通过△BOP和△AOC的面积关系求得△BOP的高,也就是点P的纵坐标,最后求出点P的坐标;
(3)先由点B和点C求出直线BC的解析式,然后设点D的坐标,从而得到点E的坐标,再表示出线段DE的长度,最后结合函数的性质求得DE的最大长度.
【解答】解:(1)将A(﹣1,0),B(3,0)代入y=﹣x2+bx+c得,
,解得:,
∴二次函数的表达式为y=﹣x2+2x+3.
(2)当x=0时,y=3,
∴C(0,3),
∴OC=3,
∵A(﹣1,0),B(3,0),
∴OA=1,OB=3,
∴S△AOC=OA OC=×3×1=,
∵S△BOP=OB |yP|=×3×|yP|,S△BOP=3S△AOC,
∴×3×|yP|=3×,
∴|yP|=3,
∵点P在x轴上方,
∴yP=3,
∴﹣x2+2x+3=3,
解得:x=0(舍)或x=2,
∴点P的坐标为(2,3).
(3)设直线BC的解析式为y=kx+b,则
,解得:,
∴直线BC的解析式为y=﹣x+3,
设点D(x,﹣x+3),则E(x,﹣x2+2x+3),
∵点D在线段BC上,
∴点E在点D的上方,
∴DE=﹣x2+2x+3﹣(﹣x+3)=﹣x2+3x=﹣(x﹣)2+,
∴当x=时,DE最大值=.
一、单选题(每题4分,共计40分)
1.(4分)抛物线y=2(x﹣1)2+6的顶点坐标是( )
A.(2,6) B.(1,6) C.(2,1) D.(﹣1,6)
2.(4分)校园里一片小小的树叶,也蕴含着“黄金分割”,如图,P为AB的黄金分割点(AP>PB),如果AB的长度为10cm,那么AP的长度为( )cm.
A.﹣1 B.2﹣2 C.5﹣5 D.10﹣10
3.(4分)将抛物线y=x2﹣4x+8向上平移1个单位长度,再向左平移3个单位长度后,得到的抛物线解析式是( )
A.y=(x+1)2+5 B.y=(x+1)2+3 C.y=(x﹣5)2+5 D.y=(x﹣5)2+3
4.(4分)若点A(﹣5,y1),B(1,y2),C(5,y3)都在反比例函数y=﹣的图象上,则y1,y2,y3的大小关系是( )
A.y1<y2<y3 B.y2<y3<y1 C.y1<y3<y2 D.y3<y1<y2
5.(4分)如图,直线l1∥l2∥l3,直线AC分别交l1,l2,l3于点A,B,C,直线DF分别交l1,l2,l3于点D,E,F,AC与DF相交于点H,如果AB=5,BH=1,CH=2,那么的值等于( )
A. B. C. D.
6.(4分)抛物线y=﹣x2+bx+c的部分图象如图所示,要使y>0,则x的取值范围是( )
A.﹣4<x<1 B.﹣3<x<1 C.x<﹣4或x>1 D.x<﹣3或x>1
7.(4分)关于二次函数y=2x2+x﹣1,下列说法正确的是( )
A.图象与y轴的交点坐标为(0,1)
B.图象的对称轴在y轴的右侧
C.当x<0时,y的值随x值的增大而减小
D.y的最小值为﹣
8.(4分)如图,在△ABC中,∠BAC=90°,AD⊥BC,则图中相似三角形共有( )
A.1对 B.2对 C.3对 D.4对
9.(4分)二次函数y=ax2+bx+c(a≠0)的图象如图,则反比例函数与一次函数y=bx﹣c在同一坐标系内的图象大致是( )
A. B.
C. D.
10.(4分)如图,在正方形ABCD中,AB=4,动点M从点A出发,以每秒1个单位长度的速度沿射线AB运动,同时动点N从点A出发,以每秒2个单位长度的速度沿折线AD→DC→CB运动,当点N运动到点B时,点M,N同时停止运动.设△AMN的面积为y,运动时间为x(s),则下列图象能大致反映y与x之间函数关系的是( )
A. B.
C. D.
二、填空题(每题5分,共计20分)
11.(5分)如图,已知在△ABC中,DE∥BC,EF∥AB,AE=2CE,AB=6,BC=9,那么四边形BDEF的周长是 .
12.(5分)如图,在平面直角坐标系中,点A是x轴上任意一点,BC∥x轴,分别交y=﹣(x<0),y=(x>0)的图像于B,C两点,若△ABC的面积是2,则k的值为 .
13.(5分)在△ABC和△DEF中,∠A=∠D=105°,AC=4cm,AB=6cm,DE=3cm,则DF= 时,△ABC与△DEF相似.
14.(5分)在直角坐标系中,点A的坐标为(3,0),若抛物线y=x2﹣2x+n﹣1与线段OA有且只有一个公共点,则n的取值范围为 .
三、解答题
15.(8分)已知线段a,b,c,且.
(1)求的值.
(2)若线段a+b+c=45,求a﹣b+c的值.
16.(8分)已知函数y=y1+y2,y1与x成正比例,y2与x成反比例,且当x=1时,y=4;当x=2时,y=5.
(1)求y与x的函数关系式;
(2)当x=4时,求y的值.
17.(8分)如图,已知反比例函数y1=的图象与一次函数y2=x+b的图象交于点A(1,4),点B(﹣4,n).
(1)求反比例函数和一次函数的表达式;
(2)求△OAB的面积;
(3)直接写出y2>y1时自变量x的取值范围.
18.(8分)已知:如图,△ABC中,∠BAC=90°,AB=AC=1,点D是BC边上的一个动点(不与B,C点重合),∠ADE=45°.求证:△ABD∽△DCE.
19.(10分)如图,点P(x,y1)与Q(x,y2)分别是两个函数图象C1与C2上的任一点.当a≤x≤b时,有﹣1≤y1﹣y2≤1成立,则称这两个函数在a≤x≤b上是“相邻函数”,否则称它们在a≤x≤b上是“非相邻函数”.例如,点P(x,y1)与Q (x,y2)分别是两个函数y=3x+1与y=2x﹣1图象上的任一点,当﹣3≤x≤﹣1时,y1﹣y2=(3x+1)﹣(2x﹣1)=x+2,通过构造函数y=x+2并研究它在﹣3≤x≤﹣1上的性质,得到该函数值的范围是﹣1≤y≤1,所以﹣1≤y1﹣y2≤1成立,因此这两个函数在﹣3≤x≤﹣1上是“相邻函数”.
(1)判断函数y=3x+1与y=2x+2在0≤x≤2上是否为“相邻函数”,并说明理由;
(2)若函数y=x2﹣x与y=x a在0≤x≤2上是“相邻函数”,求a的取值范围.
20.(10分)已知抛物线y=ax2+bx﹣3(a≠0)的对称轴为直线x=1,且抛物线经过点A(﹣1,0),它与x轴的另一交点为B,与y轴的交点为C.
(1)求这条抛物线所对应的函数表达式;
(2)在直线x=1上求点M,使△AMC的周长最小,并求△AMC的周长.
21.(12分)某社区决定把一块长50m,宽30m的矩形空地建成居民健身广场,设计方案如图,阴影区域为绿化区(四块绿化区为大小、形状都相同的矩形),空白区域为活动区,且四周的4个出口宽度相同,其宽度不小于14m,不大于26m,设绿化区较长边为xm,活动区的面积为ym2.为了想知道出口宽度的取值范围,小明同学根据出口宽度不小于14m,算出x≤18.
(1)求y与x的函数关系式并直接写出自变量x的取值范围;
(2)求活动区的最大面积;
(3)预计活动区造价为50元/m2,绿化区造价为40元/m2,若社区的此项建造投资费用不得超过72000元,求投资费用最少时活动区的出口宽度?
22.(12分)如图,Rt△ABC中,∠ACB=90°,∠B=60°,BC=2cm,D为BC的中点,若动点E以1cm/s的速度从A点出发,沿着A→B的方向运动,设E点的运动时间为t秒(0≤t<4),连接DE,当t为何值时,以B、E、D为顶点的三角形与△ABC相似?
23.(14分)如图1,在平面直角坐标系中,二次函数y=﹣x2+bx+c的图像与x轴交于点A(﹣1,0),B(3,0),与y轴交于C.
(1)求该二次函数的表达式;
(2)二次函数位于x轴上方的图像上是否存在点P,使得S△BOP=3S△AOC?如果存在,请求出点P的坐标;若不存在,请说明理由;
(3)如图2,点D为线段BC上的一个动点,过点D作DE∥y轴,交二次函数的图像于点E,求线段DE长度的最大值.
2021-2022学年安徽省六安市金安区汇文中学九年级(上)第一次月考数学试卷
参考答案与试题解析
一、单选题(每题4分,共计40分)
1.(4分)抛物线y=2(x﹣1)2+6的顶点坐标是( )
A.(2,6) B.(1,6) C.(2,1) D.(﹣1,6)
【分析】根据y=a(x﹣h)2+k,顶点坐标是(h,k),可得答案.
【解答】解:∵抛物线为y=2(x﹣1)2+6,
∴顶点坐标(1,6).
故选:B.
2.(4分)校园里一片小小的树叶,也蕴含着“黄金分割”,如图,P为AB的黄金分割点(AP>PB),如果AB的长度为10cm,那么AP的长度为( )cm.
A.﹣1 B.2﹣2 C.5﹣5 D.10﹣10
【分析】直接利用黄金分割的定义计算出AP的长即可.
【解答】解:∵P为AB的黄金分割点(AP>PB),AB=10cm,
∴AP=AB=×10=5﹣5(cm),
故选:C.
3.(4分)将抛物线y=x2﹣4x+8向上平移1个单位长度,再向左平移3个单位长度后,得到的抛物线解析式是( )
A.y=(x+1)2+5 B.y=(x+1)2+3 C.y=(x﹣5)2+5 D.y=(x﹣5)2+3
【分析】根据“上加下减,左加右减”的法则解答.
【解答】解:将抛物线y=x2﹣4x+8=(x﹣2)2+4向上平移1个单位长度,再向左平移3个单位长度后所得新抛物线的表达式为y=(x﹣2+3)2+4+1,
即y=(x+1)2+5.
故选:A.
4.(4分)若点A(﹣5,y1),B(1,y2),C(5,y3)都在反比例函数y=﹣的图象上,则y1,y2,y3的大小关系是( )
A.y1<y2<y3 B.y2<y3<y1 C.y1<y3<y2 D.y3<y1<y2
【分析】先根据反比例函数的解析式判断出函数图象所在的象限及其增减性,再由各点横坐标的值即可得出结论.
【解答】解:∵反比例函数y=﹣中,k=﹣5<0,
∴函数图象的两个分支分别位于二四象限,且在每一象限内,y随x的增大而增大.
∵﹣5<0,0<1<5,
∴点A(﹣5,y1)在第二象限,点B(1,y2),C(5,y3)在第四象限,
∴y2<y3<y1.
故选:B.
5.(4分)如图,直线l1∥l2∥l3,直线AC分别交l1,l2,l3于点A,B,C,直线DF分别交l1,l2,l3于点D,E,F,AC与DF相交于点H,如果AB=5,BH=1,CH=2,那么的值等于( )
A. B. C. D.
【分析】根据平行线分线段成比例,可以解答本题.
【解答】解:∵直线l1∥l2∥l3,
∴=,
∵AB=5,BH=1,CH=2,
∴BC=BH+CH=3,
∴=,
∴=.
故选:D.
6.(4分)抛物线y=﹣x2+bx+c的部分图象如图所示,要使y>0,则x的取值范围是( )
A.﹣4<x<1 B.﹣3<x<1 C.x<﹣4或x>1 D.x<﹣3或x>1
【分析】根据抛物线的对称性可知,图象与x轴的另一个交点是﹣3,y>0反映到图象上是指x轴上方的部分,对应的x值即为x的取值范围.
【解答】解:∵抛物线与x轴的一个交点是(1,0),对称轴是直线x=﹣1,
根据抛物线的对称性可知,抛物线与x轴的另一交点是(﹣3,0),
又图象开口向下,
∴当﹣3<x<1时,y>0.
故选:B.
7.(4分)关于二次函数y=2x2+x﹣1,下列说法正确的是( )
A.图象与y轴的交点坐标为(0,1)
B.图象的对称轴在y轴的右侧
C.当x<0时,y的值随x值的增大而减小
D.y的最小值为﹣
【分析】根据二次函数的性质和二次函数的最值即可求解.
【解答】解:A.图象与y轴的交点坐标为(0,﹣1),故A选项不符合题意;
B.图象的对称轴是直线x=在y轴的左侧,故B选项不符合题意;
C.当x时,y的值随x值的增大而减小,当x时,y的值随x值的增大而增大,故C选项不符合题意;
D.∵y=2x2+x﹣1=2(x+)2﹣,
∴当x=﹣时,y取最小值,y的最小值为﹣,故D选项符合题意;
故选:D.
8.(4分)如图,在△ABC中,∠BAC=90°,AD⊥BC,则图中相似三角形共有( )
A.1对 B.2对 C.3对 D.4对
【分析】利用直角三角形的性质和相似三角形的判定方法,可得结论.
【解答】解:∵AD⊥BC,
∴∠ADC=90°,
∵∠BAC=90°,
∴∠ADC=∠BAC,
又∵∠B=∠B,
∴△BAD∽△BCA,
∵∠ADC=∠BAC,∠C=∠C,
∴△CAD∽△CBA,
∴△BAD∽△ACD,
∴共有3对,
故选:C.
9.(4分)二次函数y=ax2+bx+c(a≠0)的图象如图,则反比例函数与一次函数y=bx﹣c在同一坐标系内的图象大致是( )
A. B.
C. D.
【分析】根据二次函数的图象找出a、b、c的正负,再结合反比例函数、一次函数系数与图象的关系即可得出结论.
【解答】解:观察二次函数图象可知:
开口向上,a>0;对称轴大于0,﹣>0,b<0;二次函数图象与y轴交点在y轴的正半轴,c>0.
∵反比例函数中k=﹣a<0,
∴反比例函数图象在第二、四象限内;
∵一次函数y=bx﹣c中,b<0,﹣c<0,
∴一次函数图象经过第二、三、四象限.
故选:C.
10.(4分)如图,在正方形ABCD中,AB=4,动点M从点A出发,以每秒1个单位长度的速度沿射线AB运动,同时动点N从点A出发,以每秒2个单位长度的速度沿折线AD→DC→CB运动,当点N运动到点B时,点M,N同时停止运动.设△AMN的面积为y,运动时间为x(s),则下列图象能大致反映y与x之间函数关系的是( )
A. B.
C. D.
【分析】根据点N的运动情况,分点N在AD,DC,CB上三种情况讨论,分别写出每种情况y和x之间的函数关系式,即可确定图象.
【解答】解:当点N在AD上时,即0<x<2
∵AM=x,AN=2x,
∴,
此时二次项系数大于0,
∴该部分函数图象开口向上,
当点N在DC上时,即2≤x<4,
此时底边AM=x,高AD=4,
∴y==2x,
∴该部分图象为直线段,
当点N在CB上时,即4≤x<6时,
此时底边AM=x,高BN=12﹣2x,
∴y=,
∵﹣1<0,
∴该部分函数图象开口向下,
故选:B.
二、填空题(每题5分,共计20分)
11.(5分)如图,已知在△ABC中,DE∥BC,EF∥AB,AE=2CE,AB=6,BC=9,那么四边形BDEF的周长是 16 .
【分析】由平行线分线段成比例得出比例式,然后证明四边形BDEF是平行四边形,得出对应边相等,即可得出结果.
【解答】解:∵AE=2CE,
∴,
∵EF∥AB
∴,
∵BC=9,
∴BF=6,
∵DE∥BC
∴,
∵AB=6,
∴BD=2;
∵EF∥AB,DE∥BC
∴四边形BDEF是平行四边形,
∴BD=EF=2,DE=BF=6,
∴四边形BDEF的周长2(2+6)=16,
故答案为:16.
12.(5分)如图,在平面直角坐标系中,点A是x轴上任意一点,BC∥x轴,分别交y=﹣(x<0),y=(x>0)的图像于B,C两点,若△ABC的面积是2,则k的值为 3 .
【分析】连接OC、OB,如图,由于BC∥x轴,根据三角形面积公式得到S△ACB=S△OCB,再利用反比例函数系数k的几何意义得到 |﹣1|+ |k|=2,然后解关于k的绝对值方程可得到满足条件的k的值.
【解答】解:连接OC、OB,如图,
∵BC∥x轴,
∴S△ACB=S△OCB,
而S△OCB= |﹣1|+ |k|,
∴ |﹣1|+ |k|=2,
而k>0,
∴k=3.
故答案为:3.
13.(5分)在△ABC和△DEF中,∠A=∠D=105°,AC=4cm,AB=6cm,DE=3cm,则DF= 2cm或4.5cm 时,△ABC与△DEF相似.
【分析】由于两相似三角形的对应边不能确定,故应分△ABC∽△DEF与△ABC∽△DFE两种情况进行讨论.
【解答】解:∵∠A=∠D,AB=6cm,AC=4cm,DE=3cm,
∴当△ABC∽△DEF时,=,即=,
解得:DF=2;
当△ABC∽△DFE时,=,
即=,
解得:DF=4.5.
综上所述,当DF=2cm或4.5cm时,△ABC和△DEF相似.
故答案为:2cm或4.5cm.
14.(5分)在直角坐标系中,点A的坐标为(3,0),若抛物线y=x2﹣2x+n﹣1与线段OA有且只有一个公共点,则n的取值范围为 ﹣2≤n<1或n=2 .
【分析】根据题意可以将函数解析式化为顶点式,由抛物线y=x2﹣2x+n﹣1与线段OA有且只有一个公共点,可以得到顶点的纵坐标为0或当x=0时y<0且当x=3时,y不小于0,从而可以求得x的取值范围.
【解答】解:∵点A的坐标为(3,0),抛物线y=x2﹣2x+n﹣1=(x﹣1)2+n﹣2与线段OA有且只有一个公共点,
∴n﹣2=0或,
解得,﹣2≤n<1或n=2,
故答案为:﹣2≤n<1或n=2.
三、解答题
15.(8分)已知线段a,b,c,且.
(1)求的值.
(2)若线段a+b+c=45,求a﹣b+c的值.
【分析】(1)根据比例的性质得出,即可得出的值;
(2)首先设,则a=4k,b=5k,c=6k,利用a+b+c=45求出k的值即可得出答案.
【解答】解:,
∴,
∴;
( 2 ) 设,则a=4k,b=5k,c=6k,
∵a+b+c=45,
∴4k+5k+6k=45,
∴k=3,
∴a=12,b=15,c=18,
∴a﹣b+c=12﹣15+18=15.
16.(8分)已知函数y=y1+y2,y1与x成正比例,y2与x成反比例,且当x=1时,y=4;当x=2时,y=5.
(1)求y与x的函数关系式;
(2)当x=4时,求y的值.
【分析】首先根据正比例与反比例函数的定义分别设出函数解析式,用待定系数法求出y与x的函数关系式,然后再代入求值.
【解答】解:设y1=k1x,y2=,则y=k1x+;
将x=1,y=4;x=2,y=5分别代入得:,
解得:k1=2,k2=2;
则y与x的函数关系式:y=2x+;
(2)把x=4代入y=2x+,
得:y=2×4+=8.
17.(8分)如图,已知反比例函数y1=的图象与一次函数y2=x+b的图象交于点A(1,4),点B(﹣4,n).
(1)求反比例函数和一次函数的表达式;
(2)求△OAB的面积;
(3)直接写出y2>y1时自变量x的取值范围.
【分析】(1)把点A坐标代入反比例函数求出m的值,也就求出了反比例函数解析式,再把点B的坐标代入反比例函数解析式求出n的值,得到点B的坐标,然后利用待定系数法即可求出一次函数解析式;
(2)先求出直线与x轴的交点坐标,从而x轴把△AOB分成两个三角形,结合点A、B的纵坐标分别求出两个三角形的面积,相加即可;
(3)根据函数的图象求得即可.
【解答】解:(1)点A(1,4)在反比例函数y1=的图象上,
∴k=1×4=4,
∴反比例函数的表达式为y1=,
∵点B(﹣4,n)也在反比例函数y1=的图象上,
∴n==﹣1,
即B(﹣4,﹣1),
把点A(1,4),点B(﹣4,﹣1)代入一次函数y2=kx+b中,,解得,
∴一次函数的表达式为y2=x+3;
故反比例函数解析式为y1=,一次函数得到解析式为y2=x+3;
(2)设直线与x轴的交点为C,
在y2=x+3中,当y=0时,得x=﹣3,
∴直线y2=x+3与x轴的交点为C(﹣3,0),
∵线段OC将△AOB分成△AOC和△BOC,
∴S△AOB=S△AOC+S△BOC=×3×4+×3×1=7.5;
(3)从图象看,当﹣4<x<0或x>1时,y2>y1.
18.(8分)已知:如图,△ABC中,∠BAC=90°,AB=AC=1,点D是BC边上的一个动点(不与B,C点重合),∠ADE=45°.求证:△ABD∽△DCE.
【分析】先判断△ABC为等腰直角三角形得到∠B=∠C=45°,再利用三角形内角和得到∠1+∠2=135°,利用平角定义得到∠2++∠3=135°,则∠1=∠3,于是可根据有两组角对应相等的两个三角形相似得到结论.
【解答】证明:∵∠BAC=90°,AB=AC=1,
∴△ABC为等腰直角三角形,
∴∠B=∠C=45°,
∴∠1+∠2=180°﹣∠B=135°,
∵∠ADE=45°,
∴∠2+∠3=135°,
∴∠1=∠3,
∵∠B=∠C,
∴△ABD∽△DCE.
19.(10分)如图,点P(x,y1)与Q(x,y2)分别是两个函数图象C1与C2上的任一点.当a≤x≤b时,有﹣1≤y1﹣y2≤1成立,则称这两个函数在a≤x≤b上是“相邻函数”,否则称它们在a≤x≤b上是“非相邻函数”.例如,点P(x,y1)与Q (x,y2)分别是两个函数y=3x+1与y=2x﹣1图象上的任一点,当﹣3≤x≤﹣1时,y1﹣y2=(3x+1)﹣(2x﹣1)=x+2,通过构造函数y=x+2并研究它在﹣3≤x≤﹣1上的性质,得到该函数值的范围是﹣1≤y≤1,所以﹣1≤y1﹣y2≤1成立,因此这两个函数在﹣3≤x≤﹣1上是“相邻函数”.
(1)判断函数y=3x+1与y=2x+2在0≤x≤2上是否为“相邻函数”,并说明理由;
(2)若函数y=x2﹣x与y=x a在0≤x≤2上是“相邻函数”,求a的取值范围.
【分析】(1)通过构建函数y=x﹣1,根据一次函数的性质可得出该函数在0≤x≤2上单调递增,分别代入x=0、x=2即可得出y的取值范围,由此即可得出结论;
(2)由函数y=x2﹣x与y=x a在0≤x≤2上是“相邻函数”,构造函数y=x2﹣(a+1)x,根据抛物线的位置不同,令其最大值≤1、最小值≥﹣1,解关于a的不等式组即可得出结论.
【解答】解:(1)函数y=3x+1与y=2x+2在0≤x≤2上是“相邻函数”,理由如下:
点P(x,y1)与Q (x,y2)分别是两个函数y=3x+1与y=2x+2图象上的任一点,
当0≤x≤2时,y1﹣y2=(3x+1)﹣(2x+2)=x﹣1,
通过构造函数y=x﹣1并研究它在0≤x≤2上的性质,得到该函数值的范围是﹣1≤y≤1,
所以﹣1≤y1﹣y2≤1成立,
因此这两个函数在0≤x≤2上是“相邻函数”.
(2)∵函数y=x2﹣x与y=x a在0≤x≤2上是“相邻函数”,
∴构造函数y=x2﹣(a+1)x,在0≤x≤2上﹣1≤y≤1.
根据抛物线y=x2﹣(a+1)x对称轴的位置不同,来考虑:
①当≤0,即a≤﹣1时(图1),
,解得:a≥,
∴此时无解;
②当0<≤1,即﹣1<a≤1时(图2),
,解得:≤a≤1,
∴≤a≤1;
③当1<≤2,即1<a≤3时(图3),
,解得:﹣3≤a≤1,
∴此时无解;
④当2<,即a>3时(图4),
,解得:a≤,
∴此时无解.
综上可知:若函数y=x2﹣x与y=x a在0≤x≤2上是“相邻函数”,则a的取值范围为≤a≤1.
20.(10分)已知抛物线y=ax2+bx﹣3(a≠0)的对称轴为直线x=1,且抛物线经过点A(﹣1,0),它与x轴的另一交点为B,与y轴的交点为C.
(1)求这条抛物线所对应的函数表达式;
(2)在直线x=1上求点M,使△AMC的周长最小,并求△AMC的周长.
【分析】(1)由抛物线的对称轴求出B(3,0),将A,B两点的坐标代入抛物线的解析式可得出关于a,b的方程组,解方程组可得出答案.
(2)直线BC与对称轴直线x=1的交点即为所求使△PAC的周长最小的点M的坐标.
【解答】解:(1)∵A(﹣1,0),
∴点A关于直线x=1的对称点是点B(3,0),
∴,
解得,
∴抛物线所对应的函数表达式为y=x2﹣2x﹣3;
(2)∵抛物线y=x2﹣2x﹣3与y轴的交点为C.
∴C(0,﹣3)
连接BC,交对称轴于点M,则此时△AMC周长最小,
设直线BC的关系式为:y=mx+n,
把B(3,0),C(0,﹣3)代入y=mx+n得,
,
解得.
∴直线BC的关系式为y=x﹣3,
当x=1时,y=1﹣3=﹣2,
∴M点坐标为(1,﹣2);
∵BC===3,AC==,
∴△AMC的周长=3+;
21.(12分)某社区决定把一块长50m,宽30m的矩形空地建成居民健身广场,设计方案如图,阴影区域为绿化区(四块绿化区为大小、形状都相同的矩形),空白区域为活动区,且四周的4个出口宽度相同,其宽度不小于14m,不大于26m,设绿化区较长边为xm,活动区的面积为ym2.为了想知道出口宽度的取值范围,小明同学根据出口宽度不小于14m,算出x≤18.
(1)求y与x的函数关系式并直接写出自变量x的取值范围;
(2)求活动区的最大面积;
(3)预计活动区造价为50元/m2,绿化区造价为40元/m2,若社区的此项建造投资费用不得超过72000元,求投资费用最少时活动区的出口宽度?
【分析】(1)根据“活动区的面积=矩形空地面积﹣阴影区域面积”列出函数解析式便可,图形可得结论;
(2)根据题意可得y与x的关系式;
(3)根据二次函数的增减性及解一元二次方程可得结论;
【解答】解:(1)根据题意,绿化区的宽为:[30﹣(50﹣2x)]÷2=x﹣10
∴y=50×30﹣4x(x﹣10)=﹣4x2+40x+1500,
∵4个出口宽度相同,其宽度不小于14m,不大于26m,
∴12≤x≤18,
∴y=﹣4x2+40x+1500(12≤x≤18);
(2)y=﹣4x2+40x+1500=﹣4(x﹣5)2+1600,
∵a=﹣4<0,抛物线的开口向下,当12≤x≤18时,y随x的增大而减小,
∴当x=12时,y最大=1404,
答:活动区的最大面积为1404m2.
(3)设投资费用为w元,
由题意得,w=50(﹣4x2+40x+1500)+40×4x(x﹣10)=﹣40(x﹣5)2+76000,
∴当w=72000时,解得:x1=﹣5(不符合题意舍去),x2=15,
∵a=﹣40<0,
∴当x≥15时,w≤72000,
又∵12≤x≤18,
∴15≤x≤18,
∴当x=18时,投资费用最少,此时出口宽度为50﹣2x=50﹣2×18=14(m),
答:投资最少时活动区的出口宽度为14m.
22.(12分)如图,Rt△ABC中,∠ACB=90°,∠B=60°,BC=2cm,D为BC的中点,若动点E以1cm/s的速度从A点出发,沿着A→B的方向运动,设E点的运动时间为t秒(0≤t<4),连接DE,当t为何值时,以B、E、D为顶点的三角形与△ABC相似?
【分析】求出AB=2BC=4cm,分两种情况:①当∠EDB=∠ACB=90°时,DE∥AC,△EBD∽△ABC,得出AE=BE=AB=2cm,即可得出t=2s;②当∠DEB=∠ACB=90°时,证出△DBE∽△ABC,得出∠BDE=∠A=30°,因此BE=BD=cm,得出AE=3.5cm,t=3.5s;即可得出结果.
【解答】解:∵∠ACB=90°,∠ABC=60°,
∴∠A=30°,
∴AB=2BC=4cm,
分两种情况:
①当∠EDB=∠ACB=90°时,
DE∥AC,△EBD∽△ABC,
∵D为BC的中点,
∴BD=CD=BC=1cm,E为AB的中点,AE=BE=AB=2cm,
∴t=2s;
②当∠DEB=∠ACB=90°时,
∵∠B=∠B,
∴△DBE∽△ABC,
∴∠BDE=∠A=30°,
∴BE=BD=cm,
∴AE=3.5cm,
∴t=3.5s;
综上所述:当以B、D、E为顶点的三角形与△ABC相似时,t的值为2或3.5;
23.(14分)如图1,在平面直角坐标系中,二次函数y=﹣x2+bx+c的图像与x轴交于点A(﹣1,0),B(3,0),与y轴交于C.
(1)求该二次函数的表达式;
(2)二次函数位于x轴上方的图像上是否存在点P,使得S△BOP=3S△AOC?如果存在,请求出点P的坐标;若不存在,请说明理由;
(3)如图2,点D为线段BC上的一个动点,过点D作DE∥y轴,交二次函数的图像于点E,求线段DE长度的最大值.
【分析】(1)将点A和点B的坐标代入函数解析式得到关于b和c的方程组,然后求得b和c的大小,最后得到解析式;
(2)先求出点C的坐标,结合点A求得△AOC的面积,然后通过△BOP和△AOC的面积关系求得△BOP的高,也就是点P的纵坐标,最后求出点P的坐标;
(3)先由点B和点C求出直线BC的解析式,然后设点D的坐标,从而得到点E的坐标,再表示出线段DE的长度,最后结合函数的性质求得DE的最大长度.
【解答】解:(1)将A(﹣1,0),B(3,0)代入y=﹣x2+bx+c得,
,解得:,
∴二次函数的表达式为y=﹣x2+2x+3.
(2)当x=0时,y=3,
∴C(0,3),
∴OC=3,
∵A(﹣1,0),B(3,0),
∴OA=1,OB=3,
∴S△AOC=OA OC=×3×1=,
∵S△BOP=OB |yP|=×3×|yP|,S△BOP=3S△AOC,
∴×3×|yP|=3×,
∴|yP|=3,
∵点P在x轴上方,
∴yP=3,
∴﹣x2+2x+3=3,
解得:x=0(舍)或x=2,
∴点P的坐标为(2,3).
(3)设直线BC的解析式为y=kx+b,则
,解得:,
∴直线BC的解析式为y=﹣x+3,
设点D(x,﹣x+3),则E(x,﹣x2+2x+3),
∵点D在线段BC上,
∴点E在点D的上方,
∴DE=﹣x2+2x+3﹣(﹣x+3)=﹣x2+3x=﹣(x﹣)2+,
∴当x=时,DE最大值=.
同课章节目录
