苏科版八年级数学上册 3.1 勾股定理(15)(课件)(共17张PPT)
文档属性
| 名称 | 苏科版八年级数学上册 3.1 勾股定理(15)(课件)(共17张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 377.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 苏科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-10-20 00:00:00 | ||
图片预览



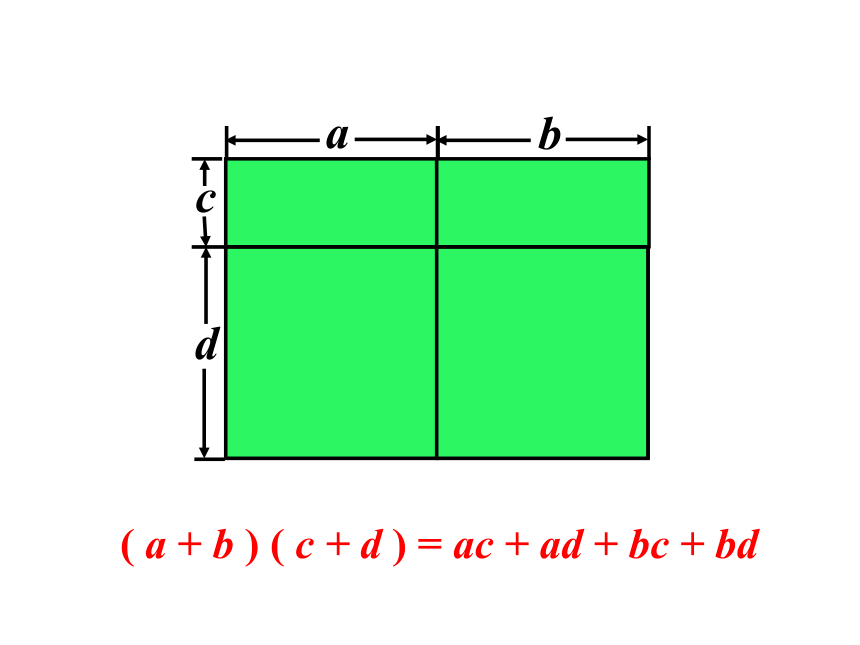


文档简介
(共17张PPT)
3.1 勾股定理
苏教版八年级(上)
3.1勾股定理(1)
d
b
a
a ( b + c + d ) = ab + ac + ad
c
方法探究
a
d
c
ab
b
ab
( a + b ) ( c + d ) = ac + ad + bc + bd
a
b
b
a
ab
b2
ab
a2
(a + b)2 = a2 + 2ab + b2
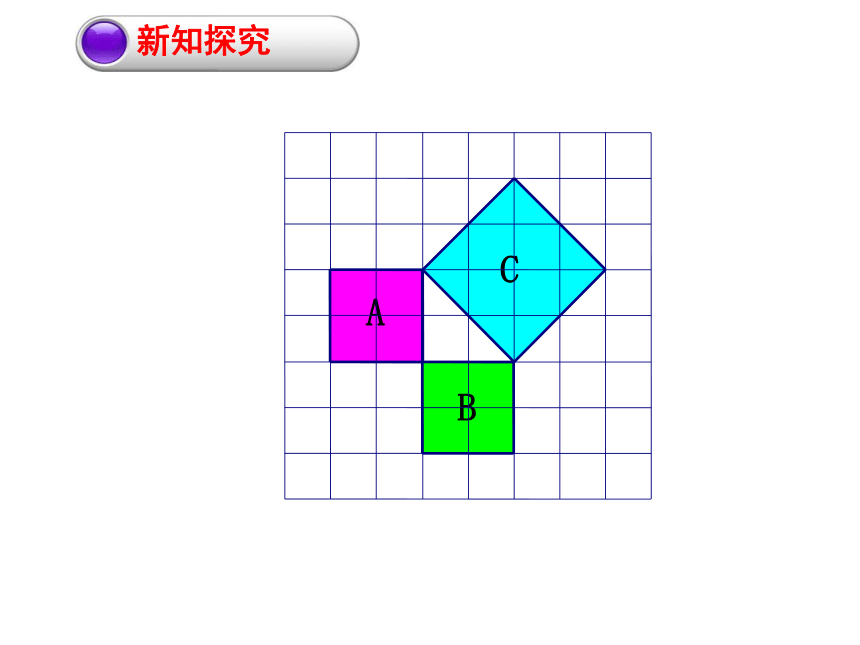
B
A
C
C
新知探究
B
C
A
a
b
c
新知探究
c
a
b
C
新知探究
C
A
B
a
b
c
新知探究
勾
股
弦
勾股定理
直角三角形两直角边的平方和等于斜边的平方.
A
a
b
c
B
C
∵在Rt△ABC中,∠C=90,
∴ a2+b2=c2.
新知生成
勾股史话
我国是最早了解勾股定理国家之一.
早在三千多年前,周朝的数学家商高就提出,
将一根直尺折成一个直角,如果勾等于三,
股等于四,那么弦就等于五,即“勾三、股四、
弦五”. 它被记载于我国古代著名的数学著作
《周髀算经》中. 这一发现,至少早于古希腊人500多年. 作为一名中国人,我们应为我国古人的博学和多思而感到自豪!
勾股定理是人类文明的成果,几乎所有拥有古代文化的民族和国家都对勾股定理有所研究. 在地球以外是否存在生命这个问题上,我国数学家华罗庚曾认为,如果外星人也拥有文明的话,我们可以用“勾股定理”的图形,作为人类探寻“外星人”并与“外星人”联系的“语言” .
1. 求下列直角三角形中未知边的长:
新知运用
2. 求下列图中未知数 x、y、z 的值:
例1 .在Rt△ABC中,∠C=90°.
(1) 已知:a=6,b=8,求c;
(2) 已知:a=40,c=41,求b;
(3) 已知:c=13,b=5,求a;
(4) 已知: a:b=3:4, c=15,求a、b.
例题分析
(1)在直角三角形中,已知两边,可求第三边;
(2)可用勾股定理建立方程.
方法小结
如图,学校有一块长方形花园,有极少数人为了避开拐角走“捷径”,在花园内走出了一条“路”,仅仅少走了 米路,却踩伤了花草。
解决问题
你的疑问、你的收获、你的想法!
反思提升
谢 谢
3.1 勾股定理
苏教版八年级(上)
3.1勾股定理(1)
d
b
a
a ( b + c + d ) = ab + ac + ad
c
方法探究
a
d
c
ab
b
ab
( a + b ) ( c + d ) = ac + ad + bc + bd
a
b
b
a
ab
b2
ab
a2
(a + b)2 = a2 + 2ab + b2
B
A
C
C
新知探究
B
C
A
a
b
c
新知探究
c
a
b
C
新知探究
C
A
B
a
b
c
新知探究
勾
股
弦
勾股定理
直角三角形两直角边的平方和等于斜边的平方.
A
a
b
c
B
C
∵在Rt△ABC中,∠C=90,
∴ a2+b2=c2.
新知生成
勾股史话
我国是最早了解勾股定理国家之一.
早在三千多年前,周朝的数学家商高就提出,
将一根直尺折成一个直角,如果勾等于三,
股等于四,那么弦就等于五,即“勾三、股四、
弦五”. 它被记载于我国古代著名的数学著作
《周髀算经》中. 这一发现,至少早于古希腊人500多年. 作为一名中国人,我们应为我国古人的博学和多思而感到自豪!
勾股定理是人类文明的成果,几乎所有拥有古代文化的民族和国家都对勾股定理有所研究. 在地球以外是否存在生命这个问题上,我国数学家华罗庚曾认为,如果外星人也拥有文明的话,我们可以用“勾股定理”的图形,作为人类探寻“外星人”并与“外星人”联系的“语言” .
1. 求下列直角三角形中未知边的长:
新知运用
2. 求下列图中未知数 x、y、z 的值:
例1 .在Rt△ABC中,∠C=90°.
(1) 已知:a=6,b=8,求c;
(2) 已知:a=40,c=41,求b;
(3) 已知:c=13,b=5,求a;
(4) 已知: a:b=3:4, c=15,求a、b.
例题分析
(1)在直角三角形中,已知两边,可求第三边;
(2)可用勾股定理建立方程.
方法小结
如图,学校有一块长方形花园,有极少数人为了避开拐角走“捷径”,在花园内走出了一条“路”,仅仅少走了 米路,却踩伤了花草。
解决问题
你的疑问、你的收获、你的想法!
反思提升
谢 谢
同课章节目录
- 第一章 全等三角形
- 1.1 全等图形
- 1.2 全等三角形
- 1.3 探索三角形全等的条件
- 数学活动 关于三角形全等的条件
- 第二章 轴对称图形
- 2.1 轴对称与轴对称图形
- 2.2 轴对称的性质
- 2.3 设计轴对称图案
- 2.4 线段、角的轴对称性
- 2.5 等腰三角形的轴对称性
- 数学活动 折纸与证明
- 第三章 勾股定理
- 3.1 勾股定理
- 3.2 勾股定理的逆定理
- 3.3 勾股定理的简单应用
- 数学活动 探寻“勾股数”
- 第四章 实数
- 4.1 平方根
- 4.2 立方根
- 4.3 实数
- 4.4 近似数
- 数学活动 有关“实数”的课题探究
- 第五章 平面直角坐标系
- 5.1 物体位置的确定
- 5.2 平面直角坐标系
- 数学活动 确定藏宝地
- 第六章 一次函数
- 6.1 函数
- 6.2 一次函数
- 6.3 一次函数的图像
- 6.4 用一次函数解决问题
- 6.5 一次函数与二元一次方程
- 6.6 一次函数、一元一次方程和一元一次不等式
- 数学活动 温度计上的一次函数
