不等式的解法课件

(共28张PPT)
一元二次不等式的解（逆向应用）
通州中专 李忠
2011年8月17日
教学过程设计流程图
2．新课教学
——情景引入
5．课堂小结
——回顾新知
6.布置作业
——加强巩固
4．巩固训练
——小试牛刀
3．例题讲解
——合作探究
1．新课导入
——温故知新
新课导入
布置作业
归纳小结
例题讲解
巩固训练
新课教学
1．新课导入
——温故知新
1、求下列不等式的解集：
(1)(x+1)(x-2)<0 ；
(2)-x2+2x+3 0 ；
(3)x2-6x+10>0 ；
(4)x2+2x+1 0 ；
(5）x2-2x+3<0 ；
（6）x2-4x+4>0 ．
帮助
帮助
帮助
帮助
帮助
帮助
(1)(x+1)(x-2)<0的解集为（-1，2）。
(2)-x2+2x+3 0的解集为｛x︱x≤-3或x≥1｝。
y　
x　
o　
1　
2　
3　
3　
2　
1　
4　
5　
第（2）题
x　
y　
o　
1　
2　
3　
3　
2　
1　
4　
5　
第（1）题
(4)x2+2x+1 0的解集为｛-1｝。
(3)x2-6x+10>0的解集为R。
x　
y　
o　
1　
2　
3　
3　
2　
1　
4　
5　
第（4）题
x　
y　
o　
1　
2　
3　
3　
2　
1　
4　
5　
第（3）题
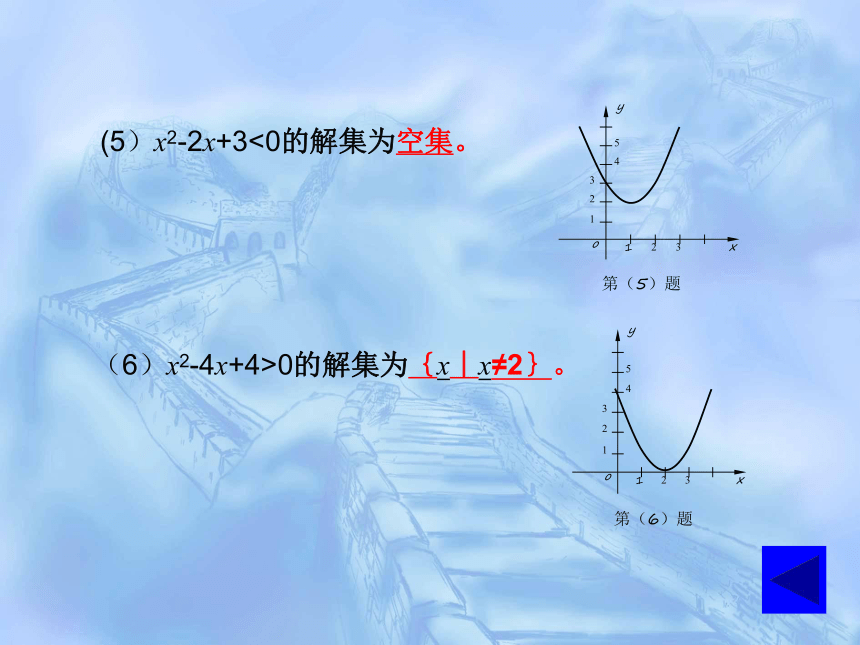
(5）x2-2x+3<0的解集为空集。
（6）x2-4x+4>0的解集为｛x︱x≠2｝。
x　
y　
o　
1　
2　
3　
3　
2　
1　
4　
5　
第（6）题
x　
y　
o　
1　
2　
3　
3　
2　
1　
4　
5　
第（5）题
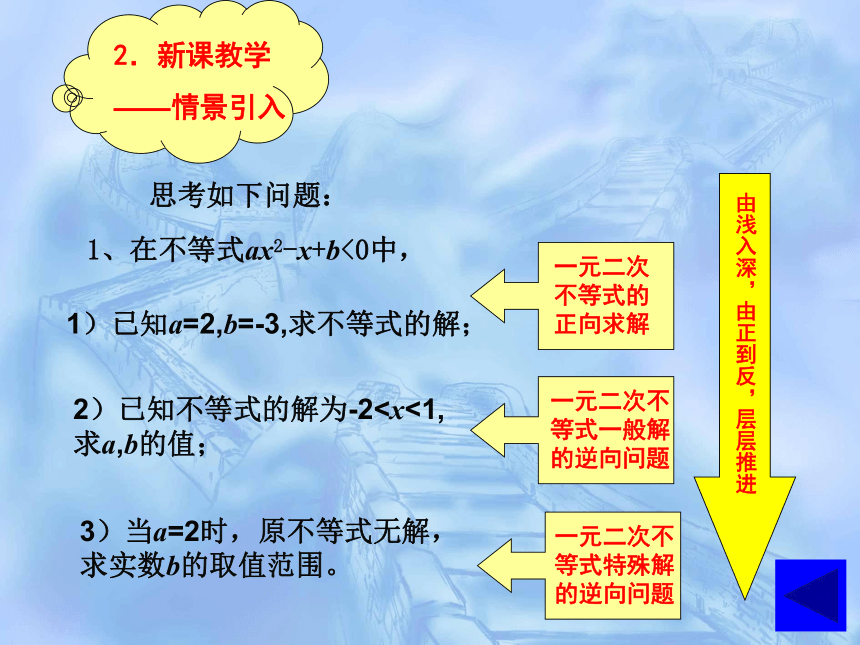
2．新课教学
——情景引入
1、在不等式ax2-x+b<0中，
3）当a=2时，原不等式无解，求实数b的取值范围。
2）已知不等式的解为-21）已知a=2,b=-3,求不等式的解；
思考如下问题：
一元二次不等式的正向求解
一元二次不等式一般解的逆向问题
一元二次不等式特殊解的逆向问题
由浅入深，由正到反，层层推进
3．例题讲解
——合作探究
例1、已知函数 y=(a+1)x2+2(a+1)x+4 的图像都在x轴上方，求实数的取值的集合。
①“函数图像都在x轴上方”，你能画出示意图吗？
②应满足什么条件？（引导学生把图形语言转化成数学符号语言）
学生思考
教师引导
学生讨论
回答
分解难点 层层推进
①该解法有无值得商榷之处？
②题目中的函数一定是二次函数吗？（引导学生考虑二次项系数等于0的情况）
最后师生共同给出例1的完整解答过程。
教师板书解法（未考虑二次项系数等于0的情况），进一步提问：
学生思考
教师引导
学生讨论
回答
分解难点 层层推进
师生小结
变式训练1：如果“图像都不在x轴上方”，结果怎样？（与例1类似）
变式训练2：“已知不等式(a+1)x2+2(a+1)x+4＜0的解为一切实数，求实数a的取值的范围。” （将以形的条件变化为数的条件）
小组讨论
合作探究
小组讨论
合作探究
变式训练 拓展提升
帮助
帮助
4．巩固训练
——小试牛刀
1、不等式a x2＋ b x ＋ 2 ＞ 0的解集为 (-1,2) ,
则 a = ， b = 。
2、不等式x2＋ b x ＋4≤0的解集为空集,
则实数b的取值范围为 。
3、不等式ax2+bx+c>0的解集为{x|x＜－1,或x＞2}, 那么不等式ax2-bx+c<0的解是____。
4、当不等式m x＋ ( 4－2m ) x ＋ m ＞ 0的解集为R时，实数m的取值范围为 ；
当上不等式无解时，实数m的取值范围为 。
5、已知集合A＝{a︱关于x的方程x2－ax＋1＝0,有实根}，B＝{a ︱不等式ax2-2x+1＞0对一切x∈R成立},则集合A= ；B= ；A∩B= 。
帮助
帮助
帮助
帮助
帮助
1、不等式a x2＋ b x ＋ 2 ＞ 0的解集为 (-1,2) ,
则 a = -1 ， b = 1 。
2、不等式x2＋ b x ＋4≤0的解集为空集,
则实数b的取值范围为 -4＜ x ＜4 。
3、不等式ax2+bx+c>0的解集为{x|x＜－1,或x＞2}, 那么不等式ax2-bx+c<0的解是-1＜x＜2。
思路点拨
由题意得：-1，2是方程ax2+bx+c=0的两根由韦达定理可得:c=-2a,b=a 且a＞0
所以不等式ax2-bx+c<0可化为：x2-x-2＜0
解得-1＜x＜2
4、当不等式m x＋ ( 4－2m ) x ＋ m ＞ 0的解集为R时，实数m的取值范围为 m＞1 ；
当上不等式无解时，实数m的取值范围为无解。
思路点拨
(1)由题意得：
m＞0且△ =(4-2m)2-4m2＜0
解得m＞1。
(2)由题意得：
m＜0且△ =(4-2m)2-4m2≤0
解得m无解。
5、已知集合A＝{a︱关于x的方程x2－ax＋1＝0,有实根}，B＝{a ︱不等式ax2-2x+1＞0对一切x∈R成立},则集合A= ；B= ；A∩B= 。
思路点拨
根据方程x2－ax＋1＝0,有实根得△≥0，解得实数a的取值范围，即得集合A
根据不等式ax2-x+1＞0对一切x∈R成立可得a＞0且△＜0，解得实数a的取值范围，即得集合B
根据交运算的 概念得A∩B
｛a︱a≤-2或a≥2｝
｛a︱a＞1 ｝
｛a︱a≥2｝
通过这节课的学习，你有什么收获？谈谈吧！
5．课堂小结
——回顾新知
1、一元二次不等式的解法规律
2、数形结合、分类讨论等数学思想方法
6．作业布置
——加强巩固
P204 1 2
补充：
1、已知函数y=(a-2)x2+2(a-4)x-4的图像都在x轴上方，求实数a的取值的集合。
2、已知关于x的方程2x2+4mx+3m-1=0有两个负数根，求实数m的取值范围。
已知函数 y=(a+1)x2+2(a+1)x+4 的图像都在x轴上方，求实数的取值的集合。