第17章函数及其图像达标测试卷(word版含答案)
文档属性
| 名称 | 第17章函数及其图像达标测试卷(word版含答案) |  | |
| 格式 | doc | ||
| 文件大小 | 261.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 华东师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-10-20 11:08:58 | ||
图片预览


文档简介
第17章达标测试卷
八年级数学 下(HS版) 时间:45分钟 满分:100分
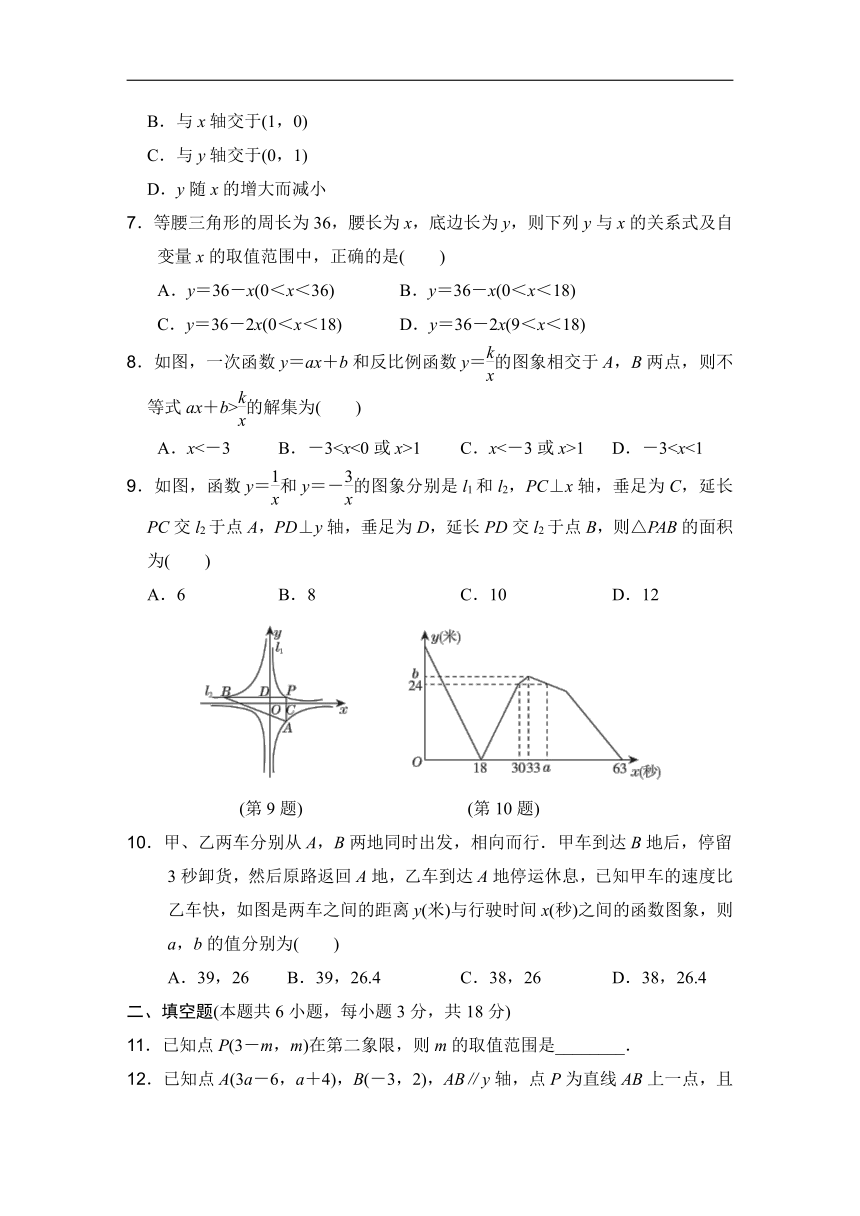
一、选择题(本题共10小题,每小题3分,共30分.在每小题给出的四个选项中,只有一项是符合要求的)
1.在函数y=中,自变量x的取值范围是( )
A.x> B.x≤ C.x≠ D.x≥
2.若点A(a-3,a+4)在y轴上,则点B(-a,-a+3)在( )
A.第二象限 B.第三象限 C.x轴上 D.y轴上
3.若函数y=(m2-3m+2)x|m|-3是反比例函数,则m的值是( )
A.1 B.-2 C.±2 D.2
4.如图所示,货车匀速通过隧道,隧道长大于货车长,从货车进入隧道开始,货车在隧道内的长度y与行驶的时间x之间的关系用图象描述大致是( )
(第4题) (第8题)
5.函数y=kx-3与y=(k≠0)在同一坐标系内的图象可能是( )
6.将直线y=x-1向上平移2个单位后得到直线y=kx+b,则下列关于直线y=kx+b的说法正确的是( )
A.经过第一、二、四象限
B.与x轴交于(1,0)
C.与y轴交于(0,1)
D.y随x的增大而减小
7.等腰三角形的周长为36,腰长为x,底边长为y,则下列y与x的关系式及自变量x的取值范围中,正确的是( )
A.y=36-x(0<x<36) B.y=36-x(0<x<18)
C.y=36-2x(0<x<18) D.y=36-2x(9<x<18)
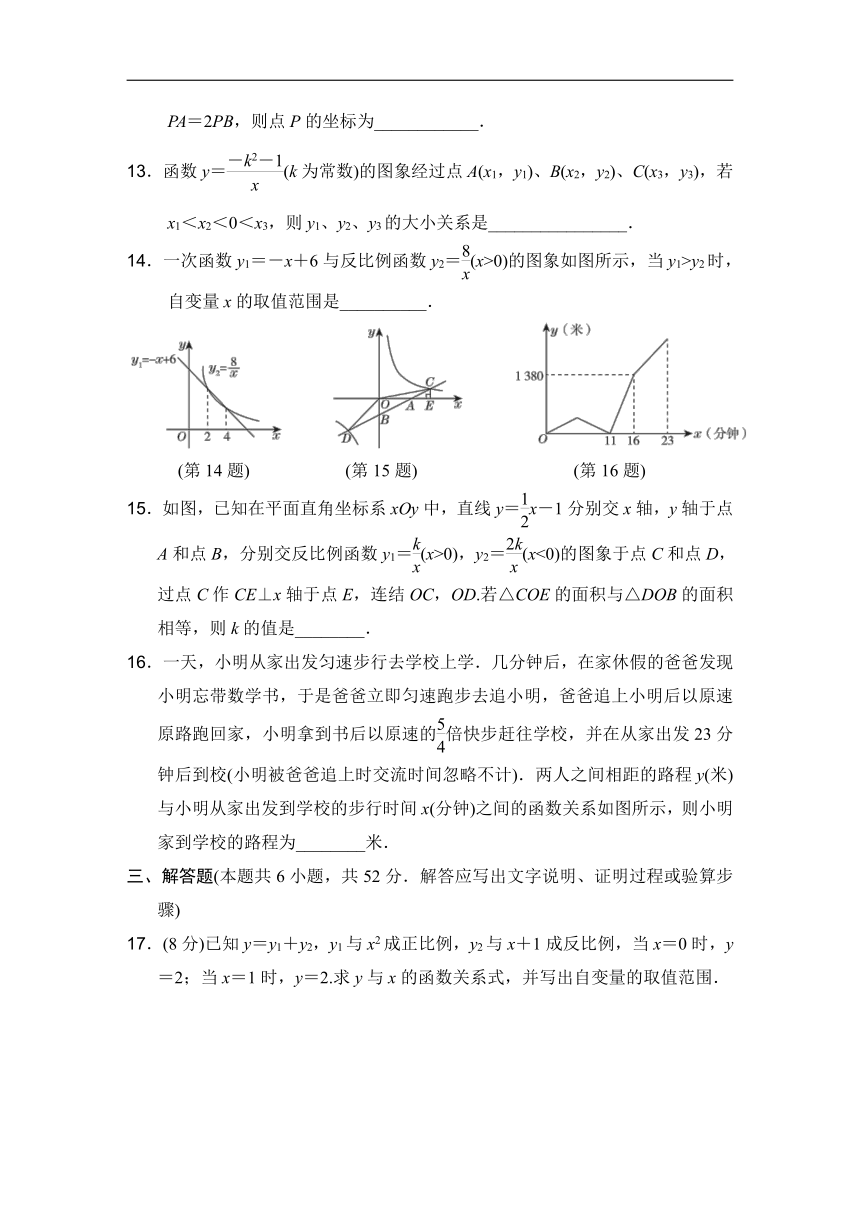
8.如图,一次函数y=ax+b和反比例函数y=的图象相交于A,B两点,则不等式ax+b>的解集为( )
A.x<-3 B.-31 C.x<-3或x>1 D.-39.如图,函数y=和y=-的图象分别是l1和l2,PC⊥x轴,垂足为C,延长PC交l2于点A,PD⊥y轴,垂足为D,延长PD交l2于点B,则△PAB的面积为( )
A.6 B.8 C.10 D.12
(第9题) (第10题)
10.甲、乙两车分别从A,B两地同时出发,相向而行.甲车到达B地后,停留3秒卸货,然后原路返回A地,乙车到达A地停运休息,已知甲车的速度比乙车快,如图是两车之间的距离y(米)与行驶时间x(秒)之间的函数图象,则a,b的值分别为( )
A.39,26 B.39,26.4 C.38,26 D.38,26.4
二、填空题(本题共6小题,每小题3分,共18分)
11.已知点P(3-m,m)在第二象限,则m的取值范围是________.
12.已知点A(3a-6,a+4),B(-3,2),AB∥y轴,点P为直线AB上一点,且PA=2PB,则点P的坐标为____________.
13.函数y=(k为常数)的图象经过点A(x1,y1)、B(x2,y2)、C(x3,y3),若x1<x2<0<x3,则y1、y2、y3的大小关系是________________.
14.一次函数y1=-x+6与反比例函数y2=(x>0)的图象如图所示,当y1>y2时,自变量x的取值范围是__________.
(第14题) (第15题) (第16题)
15.如图,已知在平面直角坐标系xOy中,直线y=x-1分别交x轴,y轴于点A和点B,分别交反比例函数y1=(x>0),y2=(x<0)的图象于点C和点D,过点C作CE⊥x轴于点E,连结OC,OD.若△COE的面积与△DOB的面积相等,则k的值是________.
16.一天,小明从家出发匀速步行去学校上学.几分钟后,在家休假的爸爸发现小明忘带数学书,于是爸爸立即匀速跑步去追小明,爸爸追上小明后以原速原路跑回家,小明拿到书后以原速的倍快步赶往学校,并在从家出发23分钟后到校(小明被爸爸追上时交流时间忽略不计).两人之间相距的路程y(米)与小明从家出发到学校的步行时间x(分钟)之间的函数关系如图所示,则小明家到学校的路程为________米.
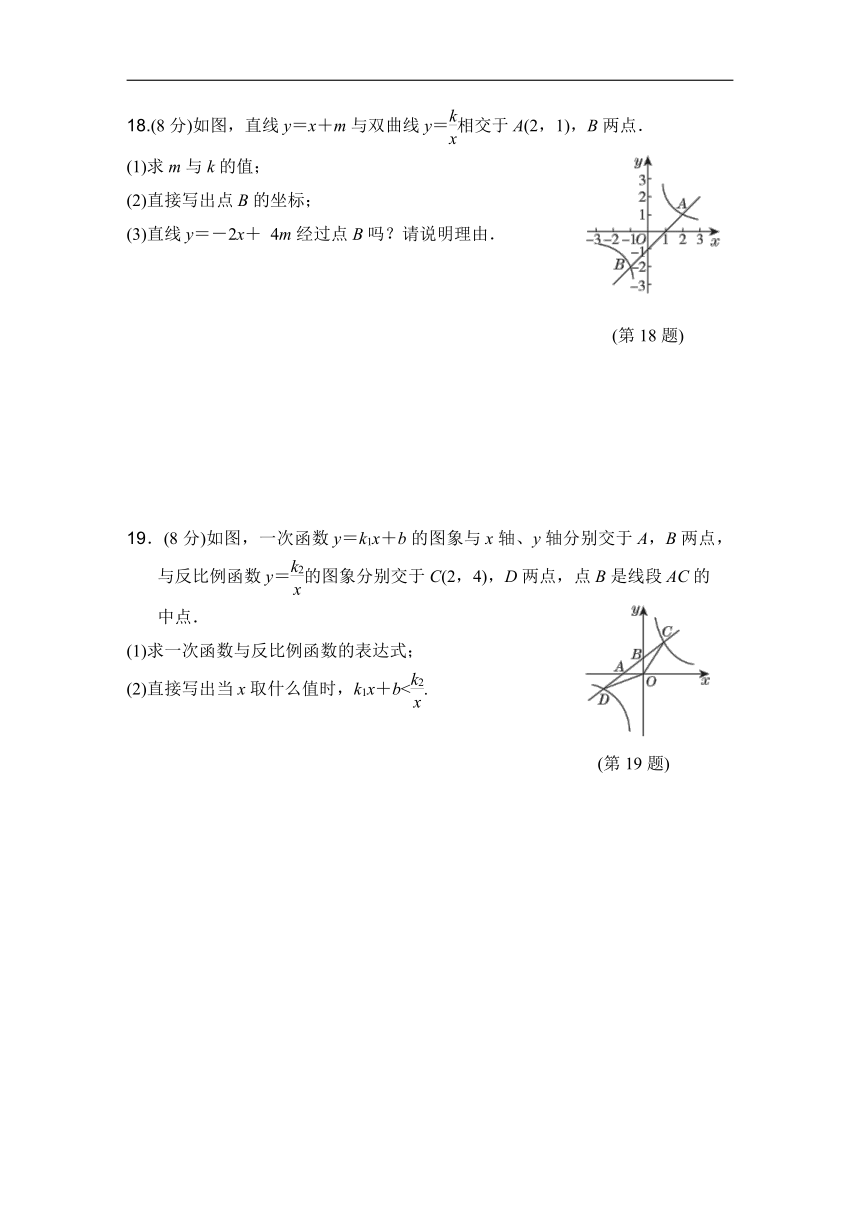
三、解答题(本题共6小题,共52分.解答应写出文字说明、证明过程或验算步骤)
17.(8分)已知y=y1+y2,y1与x2成正比例,y2与x+1成反比例,当x=0时,y=2;当x=1时,y=2.求y与x的函数关系式,并写出自变量的取值范围.
18.(8分)如图,直线y=x+m与双曲线y=相交于A(2,1),B两点.
(1)求m与k的值;
(2)直接写出点B的坐标;
(3)直线y=-2x+ 4m经过点B吗?请说明理由.
(第18题)
19.(8分)如图,一次函数y=k1x+b的图象与x轴、y轴分别交于A,B两点,与反比例函数y=的图象分别交于C(2,4),D两点,点B是线段AC的
中点.
(1)求一次函数与反比例函数的表达式;
(2)直接写出当x取什么值时,k1x+b<.
(第19题)
20.(8分)某销售公司推销一种产品,设x(件)是推销产品的数量,y(元)是付给推销员的月报酬.公司付给推销员的月报酬的两种方案如图所示,推销员可以任选一种与公司签订合同,看图解答下列问题:
(1)求每种方案y关于x的函数表达式;
(2)当选择方案一所得报酬高于选择方案二所得报酬时,求x的取值范围.
第20题)
21.(10分)甲船从A港出发顺流匀速驶向B港,乙船从B港出发逆流匀速驶向A港,甲船后面拖拽着一艘无动力小艇,行驶一段时间后,甲船发现拖拽的小艇缆绳松了,小艇不知去向,立刻原路返回寻找,找到小艇后,继续拖拽小艇顺流驶向B港.已知小艇漂流的速度和水流速度相同;甲、乙两船在静水中的速度相同.甲、乙两船到A港的距离与行驶时间之间的函数图象如图①所示.
(第21题)
(1)求乙船在逆流中行驶的速度;
(2)求甲船在逆流中行驶的路程;
(3)求甲船到A港的距离y1与行驶时间x之间的函数表达式;
(4)甲船拖拽的小艇与A港的距离和经历的时间之间的函数图象如图②所示,求点C的坐标.
22.(10分)某公司经营某种农产品,零售一箱该农产品的利润是70元,批发一箱该农产品的利润是40元.
(1)已知该公司某月卖出100箱这种农产品共获利润4 600元,问:该公司当月零售、批发这种农产品的箱数分别是多少?
(2)经营性质规定,该公司零售的数量不能多于总数量的30%,现该公司要经营1 000箱这种农产品,问:应如何规划零售和批发的数量,才能使总利润最大?最大总利润是多少?
答案
一、1.D 2.C 3.B 4.A 5.B 6.C 7.D
8.B 9.B
10.B 点拨:由题意得=,解得b=26.4,∴乙车速度为=0.8(米/秒).∵甲、乙两车的速度和为24÷(30-18)=2(米/秒),∴甲车速度为2-0.8=1.2(米/秒),
∴甲车返回追至两车距离为24米的时间为(26.4-24)÷(1.2-0.8)=6(秒),
∴a=33+6=39.故选B.
二、11.m>3 12.(-3,3)或(-3,-1)
13.y2>y1>y3 14.215.2 点拨:如图,过点D作DF⊥y轴于点F.
(第15题)
把y=0代入y=x-1,得x=2,∴OA=2.
由题意,易得S△COE=k,S△DOF=k.
∵S△DOB=S△COE=k,
∴S△DBF=S△DOF-S△DOB=k=S△DOB,
∴OB= FB.
易证△DBF≌△ABO,
∴DF=AO=2,∴点D的横坐标为-2.
∵点D在直线y=x-1上,
∴把x=-2代入y=x-1,得y=-2,
∴D(-2,-2).
又∵点D在反比例函数y2=(x<0)的图象上,
∴k=×(-2)×(-2)=2.
16.2 080
三、17.解:∵y1与x2成正比例,
y2与x+1成反比例,
∴设y1=kx2,y2=,
∵y=y1+y2,∴y=kx2+.
∵当x=0时,y=2;当x=1时,y=2,
∴解得
∴y=x2+(x≠-1).
18.解:(1)将A(2,1)的坐标代入y=x+m,
得2+m=1,解得m=-1.
将A(2,1)的坐标代入y=,得=1,
解得k=2.
(2)点B的坐标为(-1,-2).
(3)直线y=-2x+4m经过点B,理由略.
19.解:(1)∵点C(2,4)在反比例函数y=的图象上,
∴=4,
∴k2=8.
∴反比例函数的表达式为y=.
由题意易得B(0,2).
∵点B,C在一次函数y=k1x+b的图象上,
∴解得
∴一次函数的表达式为y=x+2.
(2)当020.解:(1)设方案一y关于x的函数表达式为y=kx,把(40,1 600)代入表达式,可得k=40,故方案一y关于x的函数表达式为y=40x;
设方案二y关于x的函数表达式为y=ax+b,把(40,1 400)和(0,600)代入表达式,可得a=20,b=600,故方案二y关于x的函数表达式为y=20x+600.
(2)当方案一与方案二所得报酬相同时,即40x=20x+600,解得x=30.
结合图象可得,当x>30时,选择方案一所得报酬高于选择方案二所得报酬.
21.解:(1)乙船在逆流中行驶的速度为24÷4=6(km/h).
(2)甲船在逆流中行驶的路程为
6×(2.5-2)=3(km).
(3)设甲船顺流的速度为a km/h,
由图象得,2a-3+(3.5-2.5)a=24,
解得a=9.
当0≤x≤2时,y1=9x.
当2<x≤2.5时,设y1=-6x+b1,
把x=2,y1=18代入,得b1=30,
∴y1=-6x+30.
当2.5<x≤3.5时,设y1=9x+b2,
把x=3.5,y1=24代入,得b2=-7.5,
∴y1=9x-7.5.
综上所述,y1=
(4)水流速度为(9-6)÷2=1.5(km/h),
设甲船从A港航行x h小艇缆绳松了.
根据题意,得9(2-x)=1.5(2.5-x)+3,
解得x=1.5.
1.5×9=13.5(km),
即小艇缆绳松了时甲船到A港的距离为13.5 km.
∴点C的坐标为(1.5,13.5).
22.解:(1)设该公司当月零售这种农产品x箱,批发这种农产品y箱.
依题意,得
解得
所以该公司当月零售这种农产品20箱,批发这种农产品80箱.
(2)设该公司零售这种农产品m箱,获得总利润w元,则批发这种农产品的数量为(1 000-m)箱.
依题意,得w=70m+40(1 000-m)=30m+40 000(m≤300),
因为30>0,所以w随着m的增大而增大,
所以当m=300时,w取得最大值,最大值为49 000,
此时1 000-m=700.
所以该公司应零售这种农产品300箱,批发这种农产品700箱才能使总利润最大,最大总利润是49 000元.
八年级数学 下(HS版) 时间:45分钟 满分:100分
一、选择题(本题共10小题,每小题3分,共30分.在每小题给出的四个选项中,只有一项是符合要求的)
1.在函数y=中,自变量x的取值范围是( )
A.x> B.x≤ C.x≠ D.x≥
2.若点A(a-3,a+4)在y轴上,则点B(-a,-a+3)在( )
A.第二象限 B.第三象限 C.x轴上 D.y轴上
3.若函数y=(m2-3m+2)x|m|-3是反比例函数,则m的值是( )
A.1 B.-2 C.±2 D.2
4.如图所示,货车匀速通过隧道,隧道长大于货车长,从货车进入隧道开始,货车在隧道内的长度y与行驶的时间x之间的关系用图象描述大致是( )
(第4题) (第8题)
5.函数y=kx-3与y=(k≠0)在同一坐标系内的图象可能是( )
6.将直线y=x-1向上平移2个单位后得到直线y=kx+b,则下列关于直线y=kx+b的说法正确的是( )
A.经过第一、二、四象限
B.与x轴交于(1,0)
C.与y轴交于(0,1)
D.y随x的增大而减小
7.等腰三角形的周长为36,腰长为x,底边长为y,则下列y与x的关系式及自变量x的取值范围中,正确的是( )
A.y=36-x(0<x<36) B.y=36-x(0<x<18)
C.y=36-2x(0<x<18) D.y=36-2x(9<x<18)
8.如图,一次函数y=ax+b和反比例函数y=的图象相交于A,B两点,则不等式ax+b>的解集为( )
A.x<-3 B.-3
A.6 B.8 C.10 D.12
(第9题) (第10题)
10.甲、乙两车分别从A,B两地同时出发,相向而行.甲车到达B地后,停留3秒卸货,然后原路返回A地,乙车到达A地停运休息,已知甲车的速度比乙车快,如图是两车之间的距离y(米)与行驶时间x(秒)之间的函数图象,则a,b的值分别为( )
A.39,26 B.39,26.4 C.38,26 D.38,26.4
二、填空题(本题共6小题,每小题3分,共18分)
11.已知点P(3-m,m)在第二象限,则m的取值范围是________.
12.已知点A(3a-6,a+4),B(-3,2),AB∥y轴,点P为直线AB上一点,且PA=2PB,则点P的坐标为____________.
13.函数y=(k为常数)的图象经过点A(x1,y1)、B(x2,y2)、C(x3,y3),若x1<x2<0<x3,则y1、y2、y3的大小关系是________________.
14.一次函数y1=-x+6与反比例函数y2=(x>0)的图象如图所示,当y1>y2时,自变量x的取值范围是__________.
(第14题) (第15题) (第16题)
15.如图,已知在平面直角坐标系xOy中,直线y=x-1分别交x轴,y轴于点A和点B,分别交反比例函数y1=(x>0),y2=(x<0)的图象于点C和点D,过点C作CE⊥x轴于点E,连结OC,OD.若△COE的面积与△DOB的面积相等,则k的值是________.
16.一天,小明从家出发匀速步行去学校上学.几分钟后,在家休假的爸爸发现小明忘带数学书,于是爸爸立即匀速跑步去追小明,爸爸追上小明后以原速原路跑回家,小明拿到书后以原速的倍快步赶往学校,并在从家出发23分钟后到校(小明被爸爸追上时交流时间忽略不计).两人之间相距的路程y(米)与小明从家出发到学校的步行时间x(分钟)之间的函数关系如图所示,则小明家到学校的路程为________米.
三、解答题(本题共6小题,共52分.解答应写出文字说明、证明过程或验算步骤)
17.(8分)已知y=y1+y2,y1与x2成正比例,y2与x+1成反比例,当x=0时,y=2;当x=1时,y=2.求y与x的函数关系式,并写出自变量的取值范围.
18.(8分)如图,直线y=x+m与双曲线y=相交于A(2,1),B两点.
(1)求m与k的值;
(2)直接写出点B的坐标;
(3)直线y=-2x+ 4m经过点B吗?请说明理由.
(第18题)
19.(8分)如图,一次函数y=k1x+b的图象与x轴、y轴分别交于A,B两点,与反比例函数y=的图象分别交于C(2,4),D两点,点B是线段AC的
中点.
(1)求一次函数与反比例函数的表达式;
(2)直接写出当x取什么值时,k1x+b<.
(第19题)
20.(8分)某销售公司推销一种产品,设x(件)是推销产品的数量,y(元)是付给推销员的月报酬.公司付给推销员的月报酬的两种方案如图所示,推销员可以任选一种与公司签订合同,看图解答下列问题:
(1)求每种方案y关于x的函数表达式;
(2)当选择方案一所得报酬高于选择方案二所得报酬时,求x的取值范围.
第20题)
21.(10分)甲船从A港出发顺流匀速驶向B港,乙船从B港出发逆流匀速驶向A港,甲船后面拖拽着一艘无动力小艇,行驶一段时间后,甲船发现拖拽的小艇缆绳松了,小艇不知去向,立刻原路返回寻找,找到小艇后,继续拖拽小艇顺流驶向B港.已知小艇漂流的速度和水流速度相同;甲、乙两船在静水中的速度相同.甲、乙两船到A港的距离与行驶时间之间的函数图象如图①所示.
(第21题)
(1)求乙船在逆流中行驶的速度;
(2)求甲船在逆流中行驶的路程;
(3)求甲船到A港的距离y1与行驶时间x之间的函数表达式;
(4)甲船拖拽的小艇与A港的距离和经历的时间之间的函数图象如图②所示,求点C的坐标.
22.(10分)某公司经营某种农产品,零售一箱该农产品的利润是70元,批发一箱该农产品的利润是40元.
(1)已知该公司某月卖出100箱这种农产品共获利润4 600元,问:该公司当月零售、批发这种农产品的箱数分别是多少?
(2)经营性质规定,该公司零售的数量不能多于总数量的30%,现该公司要经营1 000箱这种农产品,问:应如何规划零售和批发的数量,才能使总利润最大?最大总利润是多少?
答案
一、1.D 2.C 3.B 4.A 5.B 6.C 7.D
8.B 9.B
10.B 点拨:由题意得=,解得b=26.4,∴乙车速度为=0.8(米/秒).∵甲、乙两车的速度和为24÷(30-18)=2(米/秒),∴甲车速度为2-0.8=1.2(米/秒),
∴甲车返回追至两车距离为24米的时间为(26.4-24)÷(1.2-0.8)=6(秒),
∴a=33+6=39.故选B.
二、11.m>3 12.(-3,3)或(-3,-1)
13.y2>y1>y3 14.2
(第15题)
把y=0代入y=x-1,得x=2,∴OA=2.
由题意,易得S△COE=k,S△DOF=k.
∵S△DOB=S△COE=k,
∴S△DBF=S△DOF-S△DOB=k=S△DOB,
∴OB= FB.
易证△DBF≌△ABO,
∴DF=AO=2,∴点D的横坐标为-2.
∵点D在直线y=x-1上,
∴把x=-2代入y=x-1,得y=-2,
∴D(-2,-2).
又∵点D在反比例函数y2=(x<0)的图象上,
∴k=×(-2)×(-2)=2.
16.2 080
三、17.解:∵y1与x2成正比例,
y2与x+1成反比例,
∴设y1=kx2,y2=,
∵y=y1+y2,∴y=kx2+.
∵当x=0时,y=2;当x=1时,y=2,
∴解得
∴y=x2+(x≠-1).
18.解:(1)将A(2,1)的坐标代入y=x+m,
得2+m=1,解得m=-1.
将A(2,1)的坐标代入y=,得=1,
解得k=2.
(2)点B的坐标为(-1,-2).
(3)直线y=-2x+4m经过点B,理由略.
19.解:(1)∵点C(2,4)在反比例函数y=的图象上,
∴=4,
∴k2=8.
∴反比例函数的表达式为y=.
由题意易得B(0,2).
∵点B,C在一次函数y=k1x+b的图象上,
∴解得
∴一次函数的表达式为y=x+2.
(2)当0
设方案二y关于x的函数表达式为y=ax+b,把(40,1 400)和(0,600)代入表达式,可得a=20,b=600,故方案二y关于x的函数表达式为y=20x+600.
(2)当方案一与方案二所得报酬相同时,即40x=20x+600,解得x=30.
结合图象可得,当x>30时,选择方案一所得报酬高于选择方案二所得报酬.
21.解:(1)乙船在逆流中行驶的速度为24÷4=6(km/h).
(2)甲船在逆流中行驶的路程为
6×(2.5-2)=3(km).
(3)设甲船顺流的速度为a km/h,
由图象得,2a-3+(3.5-2.5)a=24,
解得a=9.
当0≤x≤2时,y1=9x.
当2<x≤2.5时,设y1=-6x+b1,
把x=2,y1=18代入,得b1=30,
∴y1=-6x+30.
当2.5<x≤3.5时,设y1=9x+b2,
把x=3.5,y1=24代入,得b2=-7.5,
∴y1=9x-7.5.
综上所述,y1=
(4)水流速度为(9-6)÷2=1.5(km/h),
设甲船从A港航行x h小艇缆绳松了.
根据题意,得9(2-x)=1.5(2.5-x)+3,
解得x=1.5.
1.5×9=13.5(km),
即小艇缆绳松了时甲船到A港的距离为13.5 km.
∴点C的坐标为(1.5,13.5).
22.解:(1)设该公司当月零售这种农产品x箱,批发这种农产品y箱.
依题意,得
解得
所以该公司当月零售这种农产品20箱,批发这种农产品80箱.
(2)设该公司零售这种农产品m箱,获得总利润w元,则批发这种农产品的数量为(1 000-m)箱.
依题意,得w=70m+40(1 000-m)=30m+40 000(m≤300),
因为30>0,所以w随着m的增大而增大,
所以当m=300时,w取得最大值,最大值为49 000,
此时1 000-m=700.
所以该公司应零售这种农产品300箱,批发这种农产品700箱才能使总利润最大,最大总利润是49 000元.
