第19章矩形 菱形与正方形达标测试卷(word版含答案)
文档属性
| 名称 | 第19章矩形 菱形与正方形达标测试卷(word版含答案) |  | |
| 格式 | doc | ||
| 文件大小 | 341.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 华东师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-10-20 11:17:52 | ||
图片预览




文档简介
第19章达标测试卷
八年级数学 下(HS版) 时间:45分钟 满分:100分
一、选择题(本题共10小题,每小题3分,共30分.在每小题给出的四个选项中,只有一项是符合要求的)
1.矩形具有而菱形不具有的性质是( )
A.两组对边分别平行 B.对角线相等
C.对角线互相平分 D.两组对角分别相等
2.如图,矩形ABCD的对角线交于点O,若∠AOD=120°,AC=4,则CD的长为( )
A. B. C.2 D.3
(第2题) (第3题) (第4题)
3.如图,矩形ABCD的对角线相交于点O,过点O作OG⊥AC,交AB于点G,连结CG,若∠BOG=15°,则∠BCG的度数是( )
A.15° B.15.5° C.20° D.37.5°
4.如图,在正方形ABCD中,O是对角线AC,BD的交点,过点O作OE⊥OF,分别交AB,BC于点E,F.若AE=4,CF=3,则EF的长为( )
A.7 B.5 C.4 D.3
5.如图,在矩形ABCD中,BC=8,CD=6,将△ABE沿BE折叠,使点A恰好落在对角线BD上的F处,则DE的长是( )
A.3 B. C.5 D.
(第5题) (第6题) (第8题)
6.如图,在菱形ABCD中,M,N分别在AB,CD上,且AM=CN,MN与AC交于点O,连结BO.若∠DAC=28°,则∠OBC的度数为( )
A.28° B.52° C.62° D.72°
7.在四边形ABCD中,O是对角线的交点,能判定这个四边形是正方形的条件是( )
A.AC=BD,AB∥CD,AB=CD
B.AD∥BC,∠BAD=∠BCD
C.AO=BO=CO=DO,AC⊥BD
D.AO=CO,BO=DO,AB=BC
8.如图,四边形ABCD是菱形,对角线AC,BD相交于点O,DE⊥AB于点E,若AC=8 cm,BD=6 cm,则DE=( )
A. cm B. cm C. cm D. cm
9.如图所示的矩形是由六个正方形组成的,其中最小的正方形的面积为1,则此矩形的面积为( )
A.99 B.120 C.143 D.168
(第9题) (第10题)
10.如图,正方形ABCD与等边三角形AEF的顶点A重合,将△AEF绕顶点A旋转,在旋转过程中,当BE=DF时,∠BAE的度数可能是( )
A.15° B.165° C.15°或165° D.90°
二、填空题(本题共6小题,每小题3分,共18分)
11.如图,在平面直角坐标系中, MNEF的两条对角线ME、NF交于原点O,点F的坐标是(3,2),则点N的坐标是________.
(第11题) (第12题) (第13题)
12.如图,在菱形ABCD中,AB=5,对角线BD=8,过BD的中点O作AD的垂线,交AD于点E,交BC于点F,则EF=________.
13.如图,直线l过正方形ABCD的顶点B,点A,C到直线l的距离AE,CF的长分别是1和2,则正方形的边长是________.
14.如图,在矩形ABCD中,AE=AF,连结EF,过点E作EH⊥EF交DC于点H,过点F作FG⊥EF交BC于点G,连结GH,当AB,AD满足________(数量关系)时,四边形EFGH为矩形.
(第14题) (第15题) (第16题)
15.如图,菱形ABCD的边长是5,O是两条对角线的交点,过O点的三条直线将菱形分成阴影部分和空白部分,若菱形的一条对角线的长为4,则阴影部分的面积为__________.
16.如图,在正方形ABCD中,E是AB上一点,BE=2,AE=3BE,P是AC上一动点,则PB+PE的最小值是________.
三、解答题(本题共6小题,共52分.解答应写出文字说明、证明过程或演算步骤)
17.(8分)如图,在矩形ABCD中,点E在边AB上,点F在边BC上,且BE=CF,EF⊥DF,求证:BF=CD.
(第17题)
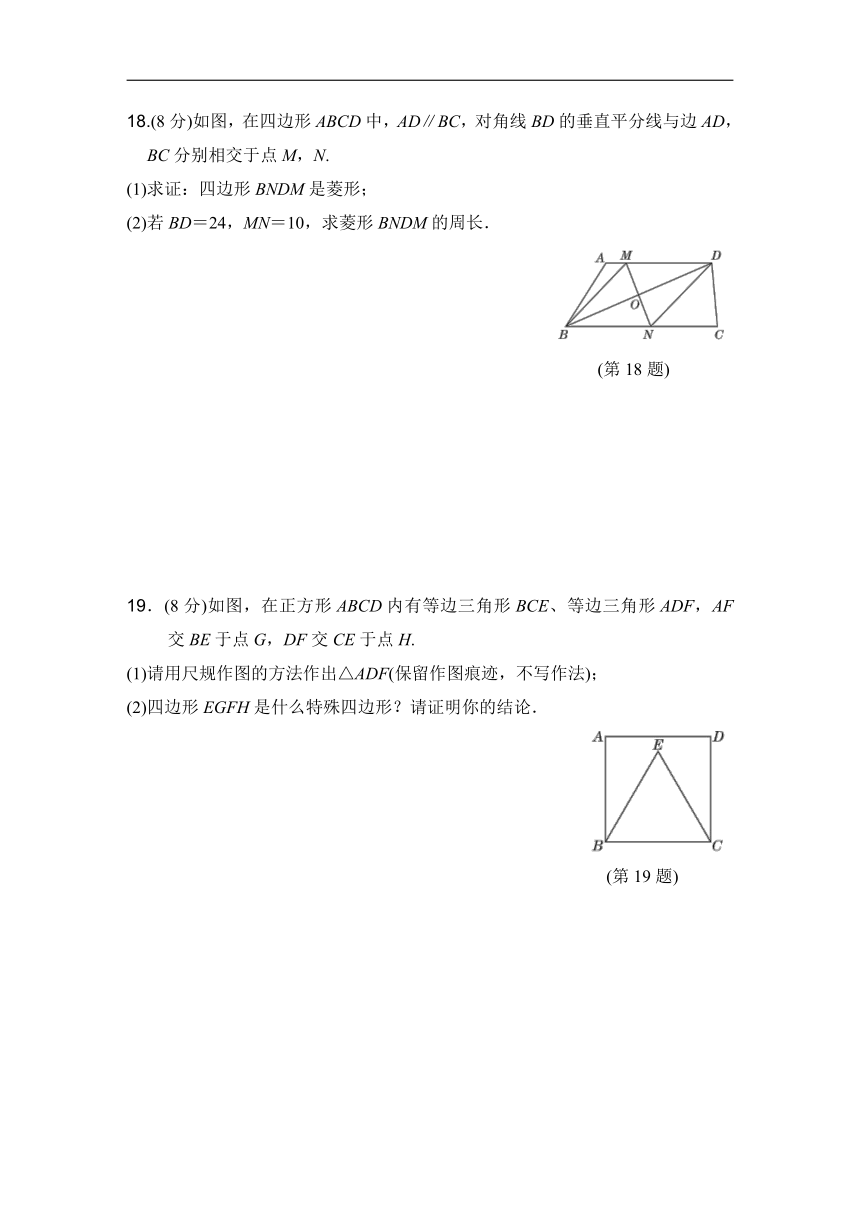
18.(8分)如图,在四边形ABCD中,AD∥BC,对角线BD的垂直平分线与边AD,BC分别相交于点M,N.
(1)求证:四边形BNDM是菱形;
(2)若BD=24,MN=10,求菱形BNDM的周长.
(第18题)
19.(8分)如图,在正方形ABCD内有等边三角形BCE、等边三角形ADF,AF交BE于点G,DF交CE于点H.
(1)请用尺规作图的方法作出△ADF(保留作图痕迹,不写作法);
(2)四边形EGFH是什么特殊四边形?请证明你的结论.
(第19题)
20.(8分)如图,点O是线段AB上的一点,OA=OC,OD平分∠AOC,交AC于点D,OF平分∠COB,CF⊥OF于点F.
(1)求证:四边形CDOF是矩形;
(2)当∠AOC=90°时,四边形CDOF是正方形吗?如果是,请说明理由.
(第20题)
21.(10分)在 ABCD中,对角线AC、BD交于点O,E是边BC延长线上的动点,过点E作EF⊥BD于F,且与CD、AD分别交于点G、H,连结OH.
(1)如图,若AC⊥AB,OF=OC,求证:FG=CG;
(2)若在点E运动的过程中,存在四边形OCGH是菱形的情形,试探究 ABCD的边和角需要满足的条件.
(第21题)
22.(10分)在 ABCD中,AC,BD交于点O,过点O作直线EF,GH,分别交平行四边形的四条边于E,G,F,H四点,连结EG,GF,FH,HE.
(1)如图①,试判断四边形EGFH的形状,并说明理由;
(2)如图②,当EF⊥GH时,四边形EGFH的形状是________;
(3)如图③,在(2)的条件下,若AC=BD,四边形EGFH的形状是________;
(4)如图④,在(3)的条件下,若AC⊥BD,试判断四边形EGFH的形状,并说明理由.
(第22题)
答案
一、1.B 2.C 3.A 4.B
5.C 点拨:在Rt△BCD中,根据勾股定理可知 BD===10,由折叠可知AE=EF,AB=BF,∠A=∠EFB=90°,
∴DF=10-6=4.在Rt△DEF中,设DE=x,则EF=8-x,由勾股定理,得x2=(8-x)2+42,解得x=5,故选C.
6.C
7.C 点拨:∵AO=BO=CO=DO,
∴四边形ABCD是矩形.
又∵AC⊥BD,
∴四边形ABCD是正方形.故选C.
8.C
9.C 点拨:如图,由题意知正方形FGHI的边长为1,设GJ的长度为x,则正方形GJKL的边长为x,正方形LKCM的边长为x,正方形EBJF的边长为x+1,正方形AEIN的边长为x+2,正方形NHMD的边长为x+3.因为四边形ABCD为矩形,所以AD=BC,所以x+2+x+3=x+1+x+x,解得x=4,所以AB=x+2+x+1=2x+3=11,BC=3x+1=13,所以矩形ABCD的面积为11×13=143.故选C.
(第9题)
10.C 点拨:①如图①,当△AEF在正方形ABCD的内部时,
(第10题)
在△ABE和△ADF中,
∴△ABE≌△ADF,
∴∠BAE=∠DAF.∵∠EAF=60°,
∴∠BAE+∠DAF=∠BAD-∠EAF=90°-60°=30°,
∴∠BAE=∠DAF=15°;
②如图②,当△AEF在正方形ABCD的外部时,同理可得∠BAE=∠DAF.∵∠EAF=60°,∴∠BAE=(360°-90°-60°)×+60°=165°.综上,∠BAE=15°或165°.故选C.
二、11.(-3,-2) 点拨:根据平行四边形的中心对称性和关于原点对称的点的坐标的特征即可写出点N的坐标.在 MNEF中,点F和点N关于原点对称.
∵点F的坐标是(3,2),
∴点N的坐标是(-3,-2).
12. 13.
14.AB=AD 15.2
16.10 点拨:∵四边形ABCD是正方形,
∴点B,D关于直线AC对称.
连结DE,交AC于P′,连结BP′,则当P在P′位置时,PB+PE的值最小.
由题易知P′B=P′D,
∴P′B+P′E=P′D+P′E=DE.
∵BE=2,AE=3BE,∴AE=6.∴AD=AB=8.
∵∠DAE=90°,
∴DE===10.
故PB+PE的最小值是10.
三、17.证明:∵四边形ABCD是矩形,
∴∠B=∠C=90°.
∵EF⊥DF,∴∠EFD=90°,
∴∠EFB+∠CFD=90°.
∵∠EFB+∠BEF=90°,
∴∠BEF=∠CFD.
在△BEF和△CFD中,
∴△BEF≌△CFD.∴BF=CD.
18.(1)证明:∵AD∥BC,
∴∠DMO=∠BNO.
∵MN是对角线BD的垂直平分线,
∴OB=OD,MN⊥BD.
在△MOD和△NOB中,
∴△MOD≌△NOB.
∴OM=ON.
∵OB=OD,
∴四边形BNDM是平行四边形.
又∵MN⊥BD,
∴四边形BNDM是菱形.
(2)解:∵四边形BNDM是菱形,
BD=24,MN=10,
∴BM=BN=DM=DN,OB=BD=12,
OM=MN=5.
在Rt△BOM中,由勾股定理得,
BM===13,
∴菱形BNDM的周长=4BM=4×13=52.
19.解:(1)如图.
(第19题)
(2)四边形EGFH是菱形.证明如下:
∵四边形ABCD是正方形,
∴∠BAD=∠ABC=90°,
∵△ADF与△BCE为等边三角形,AD=BC,
∴∠EBC=∠FAD=60°,AF=BE.
∴∠GAB=∠GBA=30°,
∴AG=BG,∠AGE=∠GAB+∠GBA=60°=∠AFD,
∴GE=GF,BE∥DF,
同理:EH∥GF,∴四边形EGFH是菱形.
20.(1)证明:∵OD平分∠AOC,OF平分∠COB,
∴∠AOC=2∠COD,∠COB=2∠COF.
又∵∠AOC+∠COB=180°,
∴2∠COD+2∠COF=180°,
∴∠COD+∠COF=90°,即∠DOF=90°.
∵OA=OC,OD平分∠AOC,
∴OD⊥AC,即∠CDO=90°.
又∵CF⊥OF,∴∠CFO=90°,
∴四边形CDOF是矩形.
(2)解:当∠AOC=90°时,四边形CDOF是正方形.理由如下:
当∠AOC=90°时,∵OA=OC,OD平分∠AOC,
∴∠ACO=∠A=45°,
∠COD=∠AOC=45°,
∴∠ACO=∠COD,∴CD=OD.
又∵四边形CDOF是矩形,
∴四边形CDOF是正方形.
21.(1)证明:连结OG.
∵四边形ABCD是平行四边形,
∴AB∥CD,
∵AC⊥AB,∴AC⊥CD,
∴∠OCG=90°,
∵EF⊥BD,∴∠OFG=90°,
在Rt△OFG和Rt△OCG中,
∴Rt△OFG≌Rt△OCG,
∴FG=CG.
(2)解:如图所示.
若四边形OCGH是菱形,
则OH=OC,OH∥CG,OC∥GH,
∵EF⊥BD,∴AC⊥BD,
∴ ABCD是菱形,
∴CD=AD,OA=OC,
∴OA=OH,
∴∠OAH=∠OHA,
∵OH∥CG,
∴∠OHA=∠ADC,
∵CD=AD,
∴∠CAD=∠DCA,
∴∠CAD=∠ADC=∠DCA,
∴△ACD是等边三角形,
∴∠ADC=60°.
即要使四边形OCGH是菱形,
ABCD的边和角需要满足的条件是
CD=AD,∠ADC=60°.
(第21题)
22.解:(1)四边形EGFH是平行四边形.
理由:∵ ABCD的对角线AC,BD交于点O,
∴点O是 ABCD的对称中心.
∴EO=FO,GO=HO.
∴四边形EGFH是平行四边形.
(2)菱形
(3)菱形
(4)四边形EGFH是正方形.理由:
∵AC=BD,∴ ABCD是矩形.
∵AC⊥BD,∴ ABCD是正方形.
∴∠BOC=90°,∠GBO=∠FCO=45°,
OB=OC.
∵EF⊥GH,∴∠GOF=90°.
∴∠BOG=∠GOF-∠BOF=∠BOC-∠BOF=∠COF.
∴△BOG≌△COF.∴OG=OF.∴GH=EF.
∵四边形EGFH是平行四边形,
∴四边形EGFH是矩形.
又∵EF⊥GH,∴四边形EGFH是正方形.
八年级数学 下(HS版) 时间:45分钟 满分:100分
一、选择题(本题共10小题,每小题3分,共30分.在每小题给出的四个选项中,只有一项是符合要求的)
1.矩形具有而菱形不具有的性质是( )
A.两组对边分别平行 B.对角线相等
C.对角线互相平分 D.两组对角分别相等
2.如图,矩形ABCD的对角线交于点O,若∠AOD=120°,AC=4,则CD的长为( )
A. B. C.2 D.3
(第2题) (第3题) (第4题)
3.如图,矩形ABCD的对角线相交于点O,过点O作OG⊥AC,交AB于点G,连结CG,若∠BOG=15°,则∠BCG的度数是( )
A.15° B.15.5° C.20° D.37.5°
4.如图,在正方形ABCD中,O是对角线AC,BD的交点,过点O作OE⊥OF,分别交AB,BC于点E,F.若AE=4,CF=3,则EF的长为( )
A.7 B.5 C.4 D.3
5.如图,在矩形ABCD中,BC=8,CD=6,将△ABE沿BE折叠,使点A恰好落在对角线BD上的F处,则DE的长是( )
A.3 B. C.5 D.
(第5题) (第6题) (第8题)
6.如图,在菱形ABCD中,M,N分别在AB,CD上,且AM=CN,MN与AC交于点O,连结BO.若∠DAC=28°,则∠OBC的度数为( )
A.28° B.52° C.62° D.72°
7.在四边形ABCD中,O是对角线的交点,能判定这个四边形是正方形的条件是( )
A.AC=BD,AB∥CD,AB=CD
B.AD∥BC,∠BAD=∠BCD
C.AO=BO=CO=DO,AC⊥BD
D.AO=CO,BO=DO,AB=BC
8.如图,四边形ABCD是菱形,对角线AC,BD相交于点O,DE⊥AB于点E,若AC=8 cm,BD=6 cm,则DE=( )
A. cm B. cm C. cm D. cm
9.如图所示的矩形是由六个正方形组成的,其中最小的正方形的面积为1,则此矩形的面积为( )
A.99 B.120 C.143 D.168
(第9题) (第10题)
10.如图,正方形ABCD与等边三角形AEF的顶点A重合,将△AEF绕顶点A旋转,在旋转过程中,当BE=DF时,∠BAE的度数可能是( )
A.15° B.165° C.15°或165° D.90°
二、填空题(本题共6小题,每小题3分,共18分)
11.如图,在平面直角坐标系中, MNEF的两条对角线ME、NF交于原点O,点F的坐标是(3,2),则点N的坐标是________.
(第11题) (第12题) (第13题)
12.如图,在菱形ABCD中,AB=5,对角线BD=8,过BD的中点O作AD的垂线,交AD于点E,交BC于点F,则EF=________.
13.如图,直线l过正方形ABCD的顶点B,点A,C到直线l的距离AE,CF的长分别是1和2,则正方形的边长是________.
14.如图,在矩形ABCD中,AE=AF,连结EF,过点E作EH⊥EF交DC于点H,过点F作FG⊥EF交BC于点G,连结GH,当AB,AD满足________(数量关系)时,四边形EFGH为矩形.
(第14题) (第15题) (第16题)
15.如图,菱形ABCD的边长是5,O是两条对角线的交点,过O点的三条直线将菱形分成阴影部分和空白部分,若菱形的一条对角线的长为4,则阴影部分的面积为__________.
16.如图,在正方形ABCD中,E是AB上一点,BE=2,AE=3BE,P是AC上一动点,则PB+PE的最小值是________.
三、解答题(本题共6小题,共52分.解答应写出文字说明、证明过程或演算步骤)
17.(8分)如图,在矩形ABCD中,点E在边AB上,点F在边BC上,且BE=CF,EF⊥DF,求证:BF=CD.
(第17题)
18.(8分)如图,在四边形ABCD中,AD∥BC,对角线BD的垂直平分线与边AD,BC分别相交于点M,N.
(1)求证:四边形BNDM是菱形;
(2)若BD=24,MN=10,求菱形BNDM的周长.
(第18题)
19.(8分)如图,在正方形ABCD内有等边三角形BCE、等边三角形ADF,AF交BE于点G,DF交CE于点H.
(1)请用尺规作图的方法作出△ADF(保留作图痕迹,不写作法);
(2)四边形EGFH是什么特殊四边形?请证明你的结论.
(第19题)
20.(8分)如图,点O是线段AB上的一点,OA=OC,OD平分∠AOC,交AC于点D,OF平分∠COB,CF⊥OF于点F.
(1)求证:四边形CDOF是矩形;
(2)当∠AOC=90°时,四边形CDOF是正方形吗?如果是,请说明理由.
(第20题)
21.(10分)在 ABCD中,对角线AC、BD交于点O,E是边BC延长线上的动点,过点E作EF⊥BD于F,且与CD、AD分别交于点G、H,连结OH.
(1)如图,若AC⊥AB,OF=OC,求证:FG=CG;
(2)若在点E运动的过程中,存在四边形OCGH是菱形的情形,试探究 ABCD的边和角需要满足的条件.
(第21题)
22.(10分)在 ABCD中,AC,BD交于点O,过点O作直线EF,GH,分别交平行四边形的四条边于E,G,F,H四点,连结EG,GF,FH,HE.
(1)如图①,试判断四边形EGFH的形状,并说明理由;
(2)如图②,当EF⊥GH时,四边形EGFH的形状是________;
(3)如图③,在(2)的条件下,若AC=BD,四边形EGFH的形状是________;
(4)如图④,在(3)的条件下,若AC⊥BD,试判断四边形EGFH的形状,并说明理由.
(第22题)
答案
一、1.B 2.C 3.A 4.B
5.C 点拨:在Rt△BCD中,根据勾股定理可知 BD===10,由折叠可知AE=EF,AB=BF,∠A=∠EFB=90°,
∴DF=10-6=4.在Rt△DEF中,设DE=x,则EF=8-x,由勾股定理,得x2=(8-x)2+42,解得x=5,故选C.
6.C
7.C 点拨:∵AO=BO=CO=DO,
∴四边形ABCD是矩形.
又∵AC⊥BD,
∴四边形ABCD是正方形.故选C.
8.C
9.C 点拨:如图,由题意知正方形FGHI的边长为1,设GJ的长度为x,则正方形GJKL的边长为x,正方形LKCM的边长为x,正方形EBJF的边长为x+1,正方形AEIN的边长为x+2,正方形NHMD的边长为x+3.因为四边形ABCD为矩形,所以AD=BC,所以x+2+x+3=x+1+x+x,解得x=4,所以AB=x+2+x+1=2x+3=11,BC=3x+1=13,所以矩形ABCD的面积为11×13=143.故选C.
(第9题)
10.C 点拨:①如图①,当△AEF在正方形ABCD的内部时,
(第10题)
在△ABE和△ADF中,
∴△ABE≌△ADF,
∴∠BAE=∠DAF.∵∠EAF=60°,
∴∠BAE+∠DAF=∠BAD-∠EAF=90°-60°=30°,
∴∠BAE=∠DAF=15°;
②如图②,当△AEF在正方形ABCD的外部时,同理可得∠BAE=∠DAF.∵∠EAF=60°,∴∠BAE=(360°-90°-60°)×+60°=165°.综上,∠BAE=15°或165°.故选C.
二、11.(-3,-2) 点拨:根据平行四边形的中心对称性和关于原点对称的点的坐标的特征即可写出点N的坐标.在 MNEF中,点F和点N关于原点对称.
∵点F的坐标是(3,2),
∴点N的坐标是(-3,-2).
12. 13.
14.AB=AD 15.2
16.10 点拨:∵四边形ABCD是正方形,
∴点B,D关于直线AC对称.
连结DE,交AC于P′,连结BP′,则当P在P′位置时,PB+PE的值最小.
由题易知P′B=P′D,
∴P′B+P′E=P′D+P′E=DE.
∵BE=2,AE=3BE,∴AE=6.∴AD=AB=8.
∵∠DAE=90°,
∴DE===10.
故PB+PE的最小值是10.
三、17.证明:∵四边形ABCD是矩形,
∴∠B=∠C=90°.
∵EF⊥DF,∴∠EFD=90°,
∴∠EFB+∠CFD=90°.
∵∠EFB+∠BEF=90°,
∴∠BEF=∠CFD.
在△BEF和△CFD中,
∴△BEF≌△CFD.∴BF=CD.
18.(1)证明:∵AD∥BC,
∴∠DMO=∠BNO.
∵MN是对角线BD的垂直平分线,
∴OB=OD,MN⊥BD.
在△MOD和△NOB中,
∴△MOD≌△NOB.
∴OM=ON.
∵OB=OD,
∴四边形BNDM是平行四边形.
又∵MN⊥BD,
∴四边形BNDM是菱形.
(2)解:∵四边形BNDM是菱形,
BD=24,MN=10,
∴BM=BN=DM=DN,OB=BD=12,
OM=MN=5.
在Rt△BOM中,由勾股定理得,
BM===13,
∴菱形BNDM的周长=4BM=4×13=52.
19.解:(1)如图.
(第19题)
(2)四边形EGFH是菱形.证明如下:
∵四边形ABCD是正方形,
∴∠BAD=∠ABC=90°,
∵△ADF与△BCE为等边三角形,AD=BC,
∴∠EBC=∠FAD=60°,AF=BE.
∴∠GAB=∠GBA=30°,
∴AG=BG,∠AGE=∠GAB+∠GBA=60°=∠AFD,
∴GE=GF,BE∥DF,
同理:EH∥GF,∴四边形EGFH是菱形.
20.(1)证明:∵OD平分∠AOC,OF平分∠COB,
∴∠AOC=2∠COD,∠COB=2∠COF.
又∵∠AOC+∠COB=180°,
∴2∠COD+2∠COF=180°,
∴∠COD+∠COF=90°,即∠DOF=90°.
∵OA=OC,OD平分∠AOC,
∴OD⊥AC,即∠CDO=90°.
又∵CF⊥OF,∴∠CFO=90°,
∴四边形CDOF是矩形.
(2)解:当∠AOC=90°时,四边形CDOF是正方形.理由如下:
当∠AOC=90°时,∵OA=OC,OD平分∠AOC,
∴∠ACO=∠A=45°,
∠COD=∠AOC=45°,
∴∠ACO=∠COD,∴CD=OD.
又∵四边形CDOF是矩形,
∴四边形CDOF是正方形.
21.(1)证明:连结OG.
∵四边形ABCD是平行四边形,
∴AB∥CD,
∵AC⊥AB,∴AC⊥CD,
∴∠OCG=90°,
∵EF⊥BD,∴∠OFG=90°,
在Rt△OFG和Rt△OCG中,
∴Rt△OFG≌Rt△OCG,
∴FG=CG.
(2)解:如图所示.
若四边形OCGH是菱形,
则OH=OC,OH∥CG,OC∥GH,
∵EF⊥BD,∴AC⊥BD,
∴ ABCD是菱形,
∴CD=AD,OA=OC,
∴OA=OH,
∴∠OAH=∠OHA,
∵OH∥CG,
∴∠OHA=∠ADC,
∵CD=AD,
∴∠CAD=∠DCA,
∴∠CAD=∠ADC=∠DCA,
∴△ACD是等边三角形,
∴∠ADC=60°.
即要使四边形OCGH是菱形,
ABCD的边和角需要满足的条件是
CD=AD,∠ADC=60°.
(第21题)
22.解:(1)四边形EGFH是平行四边形.
理由:∵ ABCD的对角线AC,BD交于点O,
∴点O是 ABCD的对称中心.
∴EO=FO,GO=HO.
∴四边形EGFH是平行四边形.
(2)菱形
(3)菱形
(4)四边形EGFH是正方形.理由:
∵AC=BD,∴ ABCD是矩形.
∵AC⊥BD,∴ ABCD是正方形.
∴∠BOC=90°,∠GBO=∠FCO=45°,
OB=OC.
∵EF⊥GH,∴∠GOF=90°.
∴∠BOG=∠GOF-∠BOF=∠BOC-∠BOF=∠COF.
∴△BOG≌△COF.∴OG=OF.∴GH=EF.
∵四边形EGFH是平行四边形,
∴四边形EGFH是矩形.
又∵EF⊥GH,∴四边形EGFH是正方形.
