4.5.2 用二分法求方程的近似解(学案)-高中数学人教A版(2019)必修第一册
文档属性
| 名称 | 4.5.2 用二分法求方程的近似解(学案)-高中数学人教A版(2019)必修第一册 |  | |
| 格式 | doc | ||
| 文件大小 | 174.1KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-10-23 09:19:03 | ||
图片预览

文档简介
第四章 指数函数与对数函数
4.5.2 用二分法求方程的近似解
学案
一、学习目标
1.通过具体实例理解二分法的概念及其适用条件,了解二分法是求方程近似解的常用方法.
2.能借助计算工具、信息技术用二分法求方程的近似解.
3.通过让学生概括二分法思想和步骤,培养学生的归纳概括能力,培养学生探究问题的能力、严谨的科学态度和创新能力. 二、基础梳理
1.二分法的概念
对于在区间[a,b]上图象连续不断且f(a)f(b)<0的函数y=f(x).通过不断地把它的零点所在区间一分为二,使所得区间的两个端点逐步逼近零点,进而得到零点近似值的方法叫做二分法.可以用二分法来求方程的近似解.
2.给定精确度,用二分法求函数y=f(x)零点x0的近似值的一般步骤如下:
(1)确定零点x0的初始区间[a,b],验证f(a)f(b)<0;
(2)求区间(a,b)的中点c;
(3)计算f(c),并进一步确定零点所在的区间:
①若f(c)=0(此时x0=c),则①c就是函数的零点,
②若f(a)f(c)<0(此时x0∈②(a,c)),则令b=c,
③若f(c)f(b)<0(此时x0∈③(c,b)),则令a=c;
(4)判断是否达到精确度ε:若<ε,则得到零点近似值a(或b);否则重复步骤(2)~(4).
三、巩固练习
1.已知函数在内有1个零点,用二分法求零点的近似值时,若精度为0.01,则至少计算中点函数值( )
A.5次 B.6次 C.7次 D.8次
2.用二分法求函数在内的唯一零点时,精度为0.001,则结束计算的条件是( )
A. B.
C. D.
3.用二分法求函数的零点可以取的初始区间是( )
A. B. C. D.
4.在用二分法求函数零点的近似值时,第一次所取的区间是,则第三次所取的区间可能是( )
A. B. C. D.
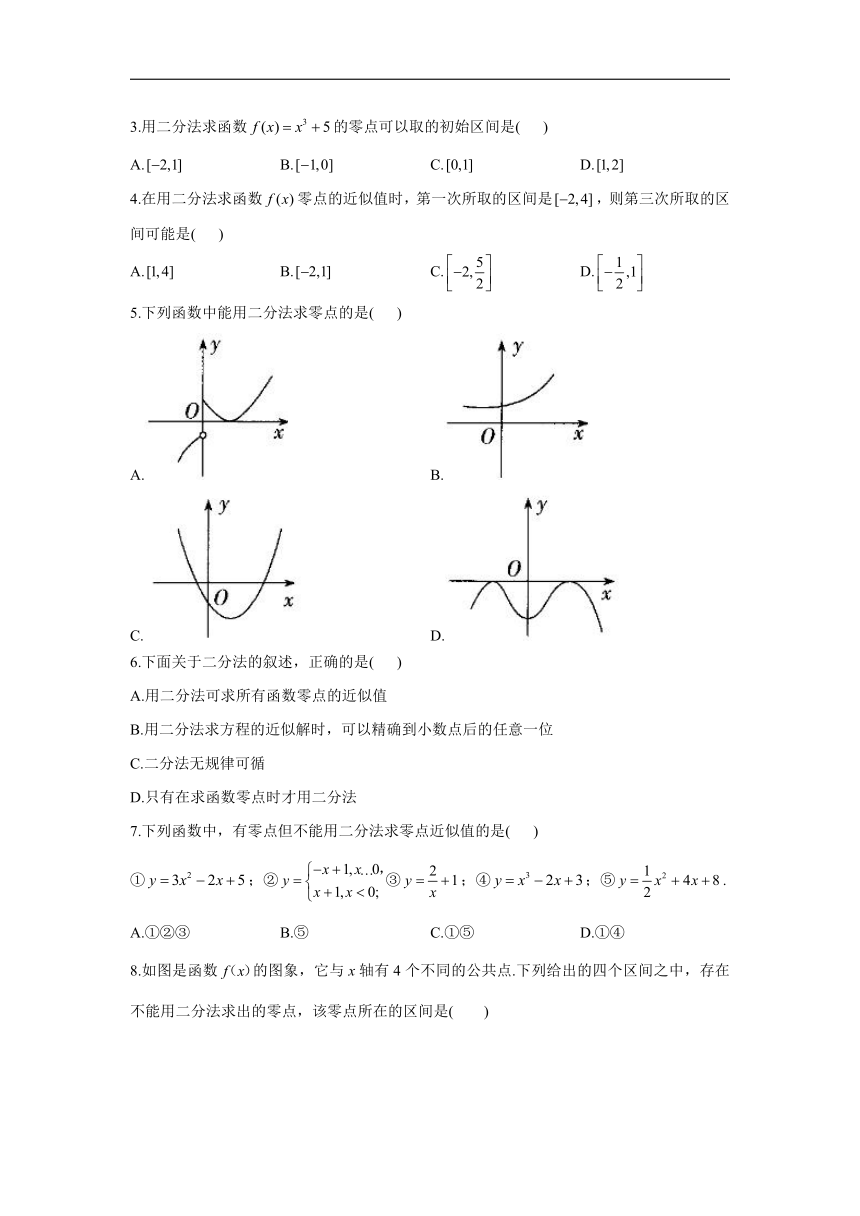
5.下列函数中能用二分法求零点的是( )
A. B.
C. D.
6.下面关于二分法的叙述,正确的是( )
A.用二分法可求所有函数零点的近似值
B.用二分法求方程的近似解时,可以精确到小数点后的任意一位
C.二分法无规律可循
D.只有在求函数零点时才用二分法
7.下列函数中,有零点但不能用二分法求零点近似值的是( )
①;②③;④;⑤.
A.①②③ B.⑤ C.①⑤ D.①④
8.如图是函数的图象,它与x轴有4个不同的公共点.下列给出的四个区间之中,存在不能用二分法求出的零点,该零点所在的区间是( )
A. B. C. D.
参考答案
巩固练习
1.答案:B
解析:设对区间二等分n次,初始区间长度为1.第1次计算后区间长度为;第2次计算后区间长度为;第3次计算后区间长度为……第5次计算后区间长度为;第6次计算后区间长度为.故至少计算6次.故选B.
2.答案:B
解析:根据二分法的步骤知当区间长度小于或等于精度的2倍时,便可结束计算,故选B.
3.答案:A
解析:因为,故可以取区间作为计算的初始区间,用二分法逐次计算.故选A.
4.答案:D
解析:第一次所取的区间是,第二次所取的区间是或,
第三次所取的区间是,,或.
5.答案:C
解析:在A和D中,函数虽有零点,但在零点左右函数值同号,因此它们都不能用二分法求零点;在B中,函数无零点;在C中,函数图像是连续不断的,且图像与x轴有交点,并且其零点左右函数值异号,所以C中的函数能用二分法求零点.故选C.
6.答案:B
解析:只有函数的图像在零点附近是连续不断的且在该零点左右函数值异号,才可以用二分法求函数的零点的近似值,故A错;二分法有规律可循,可以通过计算机来进行,故C错;求方程的近似解也可以用二分法,故D错.故选B.
7.答案:B
解析:由二分法的过程可知,函数零点左右的函数值异号时才可以用二分法求解.数①无零点,函数②③④都有变号零点,函数⑤有不变号零点-4,故不能用二分法求零点近似值.故选B.
8.答案:C
解析:用二分法只能求出变号零点的近似值,对于非变号零点,不能使用二分法.故选C.
4.5.2 用二分法求方程的近似解
学案
一、学习目标
1.通过具体实例理解二分法的概念及其适用条件,了解二分法是求方程近似解的常用方法.
2.能借助计算工具、信息技术用二分法求方程的近似解.
3.通过让学生概括二分法思想和步骤,培养学生的归纳概括能力,培养学生探究问题的能力、严谨的科学态度和创新能力. 二、基础梳理
1.二分法的概念
对于在区间[a,b]上图象连续不断且f(a)f(b)<0的函数y=f(x).通过不断地把它的零点所在区间一分为二,使所得区间的两个端点逐步逼近零点,进而得到零点近似值的方法叫做二分法.可以用二分法来求方程的近似解.
2.给定精确度,用二分法求函数y=f(x)零点x0的近似值的一般步骤如下:
(1)确定零点x0的初始区间[a,b],验证f(a)f(b)<0;
(2)求区间(a,b)的中点c;
(3)计算f(c),并进一步确定零点所在的区间:
①若f(c)=0(此时x0=c),则①c就是函数的零点,
②若f(a)f(c)<0(此时x0∈②(a,c)),则令b=c,
③若f(c)f(b)<0(此时x0∈③(c,b)),则令a=c;
(4)判断是否达到精确度ε:若<ε,则得到零点近似值a(或b);否则重复步骤(2)~(4).
三、巩固练习
1.已知函数在内有1个零点,用二分法求零点的近似值时,若精度为0.01,则至少计算中点函数值( )
A.5次 B.6次 C.7次 D.8次
2.用二分法求函数在内的唯一零点时,精度为0.001,则结束计算的条件是( )
A. B.
C. D.
3.用二分法求函数的零点可以取的初始区间是( )
A. B. C. D.
4.在用二分法求函数零点的近似值时,第一次所取的区间是,则第三次所取的区间可能是( )
A. B. C. D.
5.下列函数中能用二分法求零点的是( )
A. B.
C. D.
6.下面关于二分法的叙述,正确的是( )
A.用二分法可求所有函数零点的近似值
B.用二分法求方程的近似解时,可以精确到小数点后的任意一位
C.二分法无规律可循
D.只有在求函数零点时才用二分法
7.下列函数中,有零点但不能用二分法求零点近似值的是( )
①;②③;④;⑤.
A.①②③ B.⑤ C.①⑤ D.①④
8.如图是函数的图象,它与x轴有4个不同的公共点.下列给出的四个区间之中,存在不能用二分法求出的零点,该零点所在的区间是( )
A. B. C. D.
参考答案
巩固练习
1.答案:B
解析:设对区间二等分n次,初始区间长度为1.第1次计算后区间长度为;第2次计算后区间长度为;第3次计算后区间长度为……第5次计算后区间长度为;第6次计算后区间长度为.故至少计算6次.故选B.
2.答案:B
解析:根据二分法的步骤知当区间长度小于或等于精度的2倍时,便可结束计算,故选B.
3.答案:A
解析:因为,故可以取区间作为计算的初始区间,用二分法逐次计算.故选A.
4.答案:D
解析:第一次所取的区间是,第二次所取的区间是或,
第三次所取的区间是,,或.
5.答案:C
解析:在A和D中,函数虽有零点,但在零点左右函数值同号,因此它们都不能用二分法求零点;在B中,函数无零点;在C中,函数图像是连续不断的,且图像与x轴有交点,并且其零点左右函数值异号,所以C中的函数能用二分法求零点.故选C.
6.答案:B
解析:只有函数的图像在零点附近是连续不断的且在该零点左右函数值异号,才可以用二分法求函数的零点的近似值,故A错;二分法有规律可循,可以通过计算机来进行,故C错;求方程的近似解也可以用二分法,故D错.故选B.
7.答案:B
解析:由二分法的过程可知,函数零点左右的函数值异号时才可以用二分法求解.数①无零点,函数②③④都有变号零点,函数⑤有不变号零点-4,故不能用二分法求零点近似值.故选B.
8.答案:C
解析:用二分法只能求出变号零点的近似值,对于非变号零点,不能使用二分法.故选C.
同课章节目录
- 第一章 集合与常用逻辑用语
- 1.1 集合的概念
- 1.2 集合间的基本关系
- 1.3 集合的基本运算
- 1.4 充分条件与必要条件
- 1.5 全称量词与存在量词
- 第二章 一元二次函数、方程和不等式
- 2.1 等式性质与不等式性质
- 2.2 基本不等式
- 2.3 二次函数与一元二次方程、不等式
- 第三章 函数概念与性质
- 3.1 函数的概念及其表示
- 3.2 函数的基本性质
- 3.3 幂函数
- 3.4 函数的应用(一)
- 第四章 指数函数与对数函数
- 4.1 指数
- 4.2 指数函数
- 4.3 对数
- 4.4 对数函数
- 4.5 函数的应用(二)
- 第五章 三角函数
- 5.1 任意角和弧度制
- 5.2 三角函数的概念
- 5.3 诱导公式
- 5.4 三角函数的图象与性质
- 5.5 三角恒等变换
- 5.6 函数 y=Asin( ωx + φ)
- 5.7 三角函数的应用
