3.2 机械波多解问题 专题练—2021-2022学年高二上学期物理人教版(2019)选择性必修第一册(Word含答案)
文档属性
| 名称 | 3.2 机械波多解问题 专题练—2021-2022学年高二上学期物理人教版(2019)选择性必修第一册(Word含答案) |  | |
| 格式 | doc | ||
| 文件大小 | 370.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版(2019) | ||
| 科目 | 物理 | ||
| 更新时间 | 2021-10-20 12:33:15 | ||
图片预览



文档简介
第三章 机械波多解问题 专题练
(总分100 60分钟)
选择题(共10小题,每题6分,共60分)
1.一振动周期为T,振幅为A,位于x=0点的波源从平衡位置沿y轴正方向开始做简谐运动。该波源产生的一维简谐横波沿x轴正方向传播,波速为v,传播过程中无能量损失,一段时间后,该振动传播至某质点P,关于质点P振动的说法正确的是( )
A.振幅一定为A
B.周期一定为T
C.速度的最大值一定为v
D.开始振动的方向沿y轴向上或向下取决于它离波源的距离
2.一列简谐横波沿直线由A向B传播,A、B相距0.45 m,如图所示是A处质点的振动图象。当A处质点运动到波峰位置时,B处质点刚好到达平衡位置且向y轴正方向运动,这列波的波速可能是( )
A.4.5 m/s B.3.0 m/s
C.1.5 m/s D.0.7 m/s
3.一列简谐波在t时刻的波形如图中实线所示,此时刻质点M的运动方向向上,经过时间Δt的波形如图中虚线所示,若振动周期为T,则( )
A.Δt一定为 B.Δt可能为
C.Δt一定为 D.Δt可能为
4.简谐横波某时刻的波形如图所示,由此图可知( )
A.若质点A向下运动,则波是从左向右传播的
B.若质点B向上运动,则波是从左向右传播的
C.若波从右向左传播,则质点C向下运动
D.若波从右向左传播,则质点D向上运动
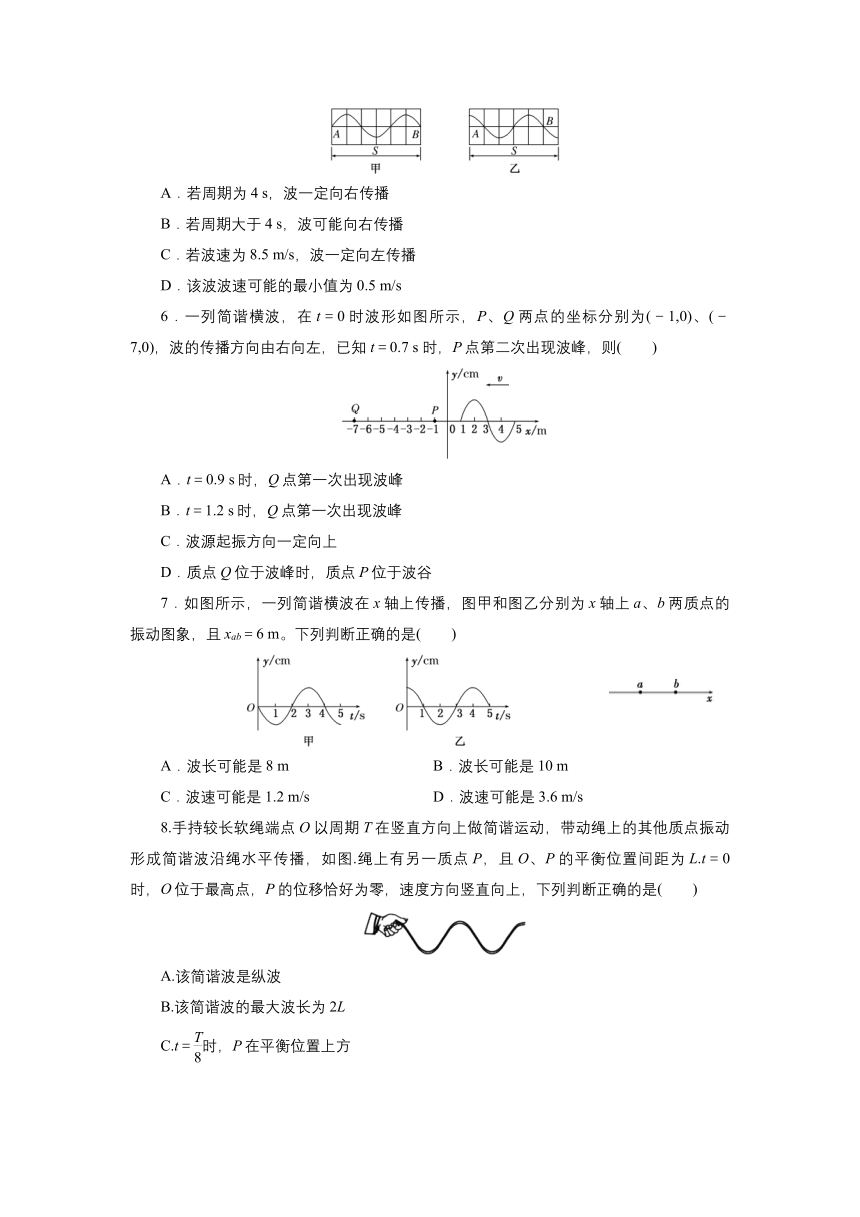
5.一列横波沿直线传播,在波的传播方向上有A、B两点,在t时刻A、B两点间形成的波形如图甲所示,在(t+3 s)时刻A、B两点间形成的波形如图乙所示,已知A、B两点间距离s=9 m,则以下说法中正确的是
A.若周期为4 s,波一定向右传播
B.若周期大于4 s,波可能向右传播
C.若波速为8.5 m/s,波一定向左传播
D.该波波速可能的最小值为0.5 m/s
6.一列简谐横波,在t=0时波形如图所示,P、Q两点的坐标分别为(-1,0)、(-7,0),波的传播方向由右向左,已知 t=0.7 s 时,P点第二次出现波峰,则( )
A.t=0.9 s时,Q点第一次出现波峰
B.t=1.2 s时,Q点第一次出现波峰
C.波源起振方向一定向上
D.质点Q位于波峰时,质点P位于波谷
7.如图所示,一列简谐横波在x轴上传播,图甲和图乙分别为x轴上a、b两质点的振动图象,且xab=6 m。下列判断正确的是( )
A.波长可能是8 m B.波长可能是10 m
C.波速可能是1.2 m/s D.波速可能是3.6 m/s
8.手持较长软绳端点O以周期T在竖直方向上做简谐运动,带动绳上的其他质点振动形成简谐波沿绳水平传播,如图.绳上有另一质点P,且O、P的平衡位置间距为L.t=0时,O位于最高点,P的位移恰好为零,速度方向竖直向上,下列判断正确的是( )
A.该简谐波是纵波
B.该简谐波的最大波长为2L
C.t=时,P在平衡位置上方
D.t=时,P的速度方向竖直向上
9.一列简谐横波沿x轴正方向传播,t时刻波形图如图10中的实线所示,此时波刚好传到P点,t+0.6 s时刻的波形如图中的虚线所示,a、b、c、P、Q是介质中的质点,则下列说法正确的是( )
A.这列波的波速可能为50 m/s
B.质点a在这段时间内通过的路程一定小于30 cm
C.质点c在这段时间内通过的路程可能为60 cm
D.若周期T=0.8 s,则在t+0.5 s时刻,质点b、P的位移相同
E.若周期T=0.8 s,从t+0.4 s时刻开始计时,则质点c的振动方程为x=0.1sin(πt) m
10. 如图,一列简谐横波沿x轴正方向传播,实线为t=0时的波形图,虚线为t=0.5 s时的波形图.已知该简谐波的周期大于0.5 s.关于该简谐波,下列说法正确的是( )
A.波长为2 m
B.波速为6 m/s
C.频率为1.5 Hz
D.t=1 s时,x=1 m处的质点处于波峰
E.t=2 s时,x=2 m处的质点经过平衡位置
计算题(共4小题,40分)
11.如图所示,简谐横波在t时刻的波形如实线所示,经过Δt=3 s,其波形如虚线所示。已知图中x1与x2相距1 m,波的周期为T,且2T<Δt<4T。则可能的最小波速为________ m/s,最小周期为________ s。
12.如图所示,实线为t1=0时刻的图象,虚线为t2=0.1 s时刻的波形,求:
(1)若波的传播方向为+x方向,周期T>0.1 s,波速多大;
(2)若波的传播方向为-x方向,周期T>0.1 s,波速多大;
(3)若波速为450 m/s,波沿什么方向传播。
13. 如图所示,实线是某时刻的波形图线,虚线是0.2 s后的波形图线。
(1)若波向左传播,求它传播的距离及最小距离;
(2)若波向右传播,求它的周期及最大周期;
(3)若波速为35 m/s,求波的传播方向。
14. 如图所示实线是一列简谐横波在t1=0时刻的波形,虚线是这列波在t2=0.5 s时刻的波形,这列波的周期T符合:3T(1)若波向右传播,波速多大?
(2)若波向左传播,波速多大?
(3)若波速大小为74 m/s,波速方向如何?
答案及解析
1.解析:选AB 机械波将波源的振动形式和能量向外传递,对简谐波而言,介质中各振动质点的振幅和周期都与波源的相同,选项A、B正确;质点P的振动速度不是波的传播速度v,选项C错误;质点P开始振动的方向与波源开始振动的方向相同,与它们之间的距离无关,选项D错误。
2.解析:选A 如图所示,当A在波峰,B在平衡位置向上振动时,A、B两点间的距离与波长的关系为(n+)λ=0.45 m得:λ= m。由振动图象可知,T=0.4 s,所以波速v== m/s,当n=0时,v=4.5 m/s, n=1时,v=0.9 m/s。故A正确。
3.解析:选D 由M点的振动方向向上可判定波沿x轴负方向传播,可认为题图中虚线是由实线经过n+T(n=0,1,2,3…)的时间得到的,故Δt可能是T,D正确。
4.解析:选BD 如果波从左向右传播,则A、B两点都向上运动,C、D两点都向下运动,可知选项A错误,B正确;如果波从右向左传播,则A、B两点都向下运动,C、D两点都向上运动,可知选项C错误,D正确。
5.解析:选ACD 若波向右传播,3 s=T1,(n=0,1,2,……),T1= s;若波向左传播,3 s=T2,(n=0,1,2,……),T2= s;由于n是整数,当T=4 s时,符合T1通项,波向右传播。故A正确;由上分析,波向右传播的周期T≤4 s,故B错误;由题图可知波长λ=6 m,若波速为8.5 m/s,波传播的距离为x=vt=8.5×3 m=4λ,根据波形的平移,波一定向左传播。故C正确;波传播的最小距离为向左传播1.5 m,波速可能的最小值为v== m/s=0.5 m/s。故D正确。
6.解析:选ACD 由题图知波长λ=4 m,第二次波峰到达P点所需时间为T=0.7 s,得T=0.4 s,波速v= m/s=10 m/s。第一次波峰传播到Q点,传播距离Δx=2 m-(-7 m)=9 m,所需时间Δt= s=0.9 s,故选项A正确,B错误;P、Q两点间距6 m=λ,振动情况相反,选项D正确;波的最前方x=1 m 处的质点正处于平衡位置向上运动,由此可知波源起振方向向上,选项C正确。
7.解析:选AC 若波是从b向a传播,则a、b的振动相差n+个周期,距离相差n+个波长,则n+λ1=6 m,即λ1= m(n=0,1,2,3,…),同理,波从a向b传播时,λ2= m(n=0,1,2,…),由此知选项A正确,B错误;根据波速公式v=,波对应的传播速度分别为v1= m/s(n=0,1,2,…),v2= m/s(n=0,1,2,…),由此知选项C正确,D错误。
8.答案 C
解析 绳波中质点的振动方向与波的传播方向垂直,属于横波,故A错误;根据波形图和波的传播方向可知,位移恰好为零且速度方向竖直向上的质点与O点的距离应为L=λ,其中n=0、1、2……,波长λ=,可知当n=0时有波长的最大值,最大值为λm=4L,故B错误;0~内P由平衡位置振动到波峰,~内P由波峰回到平衡位置,可知t=时P在平衡位置上方向上振动,t=时P在平衡位置上方向下振动,故C正确,D错误.
9.解析 由波形图可知波长λ=40 m,且0.6 s=nT+T(n=0,1,2,…),解得周期T= s(n=0,1,2,…)。当n=0时,T=0.8 s,波速v==50 m/s,选项A正确;由传播方向沿x轴正方向可知质点a在t时刻向上运动,当n=0时,T=0.8 s,则质点a在这段时间内通过的路程小于30 cm,当n=1时,T= s,质点a在这段时间内通过的路程大于30 cm,选项B错误;若n=1,则T= s,波传播到c点所用时间为T,0.6 s=,质点c振动的时间为T-T=T,故在这段时间内质点c通过的路程则为6A=60 cm,选项C正确;若T=0.8 s,t+0.5 s时刻,质点b、P的位移均为负值,大小相等,选项D正确;若T=0.8 s,从t+0.4 s时刻开始计时,则质点c的振动方程为y=0.1cos(πt) m,选项E错误。
答案 ACD
10.答案 BCE
解析 由题图波形图可知,波长λ=4 m,故A错误;横波沿x轴正方向传播,实线为t=0时的波形图,虚线为t=0.5 s时的波形图,又该简谐波的周期大于0.5 s,则波传播的距离Δx=λ,T=0.5 s,故周期T= s,频率为1.5 Hz,波速v=λf=6 m/s,故B、C正确;t=1 s=T时,x=1 m处的质点处于波谷位置,故D错误;t=2 s=3T时,x=2 m处的质点正经过平衡位置向上运动,故E正确.
11.解析:由题图可知波长为λ=7 m。若波向右传播,则Δt=T+nT,故T=,结合题目可知n=2,3;若波向左传播,则Δt=T+mT,故T=,结合题目可知m=2,3。当波向右传播,且n=2时,周期T最大,为T= s,波速最小,最小波速为v== m/s=5 m/s。当波向左传播,且m=3时,周期最小,最小周期为T= s。
答案:5
12.解析:(1)若波沿+x方向传播,根据t与周期T的关系:由题图可直接读出波长λ=20 m。
t=0.1 s=(n+)T,周期T为:
T= s。
当周期T>0.1 s时,n=0,则
T=0.4 s,
则波速为:v==50 m/s。
(2)当波向-x传播时,0.1=(n+)T,T= s,当周期T>0.1 s时,n=0,则T= s
则波速为:v==150 m/s。
(3)x=vt=450×0.1 m=45 m=2λ+λ,波沿+x方向传播。
答案:(1)50 m/s (2)150 m/s
(3)沿+x方向传播
13.[解析] (1)由题图知,λ=4 m,若波向左传播,传播的距离可能值为Δx=nλ+λ=(4n+3)m(n=0,1,2,…)
最小距离为Δxmin=3 m。
(2)若波向右传播,Δx=nλ+λm,所用时间为Δt=n+T=0.2 s,故T= s(n=0,1,2,…),所以Tmax=0.8 s。
(3)Δx=v·Δt=35×0.2 m=7 m=(λ+3)m,所以波向左传播。
[答案] (1)Δx=(4n+3) m(n=0,1,2,…) 3 m (2)T= s(n=0,1,2,…) 0.8 s (3)波向左传播
14.答案 (1)54 m/s (2)58 m/s (3)波向左传播
解析 (1)由题目中波形图知λ=8 m,
波向右传播时,传播距离Δx满足
Δx=kλ+λ(k=0,1,2,3…)
则传播时间满足Δt=kT+T(k=0,1,2,3…)
由于3T因此k取3
故Δt=3T+T,波速v=,
解得v=54 m/s.
(2)波向左传播时,传播距离Δx满足
Δx=kλ+λ(k=0,1,2,3…)
传播时间满足Δt=kT+T(k=0,1,2,3…)
由3T故Δt=3T+T,波速v=,
解得v=58 m/s.
(3)波速大小为74 m/s时,波在Δt时间内传播的距离为Δx=vΔt=74×0.5 m=37 m=4λ+λ,所以波向左传播.
(总分100 60分钟)
选择题(共10小题,每题6分,共60分)
1.一振动周期为T,振幅为A,位于x=0点的波源从平衡位置沿y轴正方向开始做简谐运动。该波源产生的一维简谐横波沿x轴正方向传播,波速为v,传播过程中无能量损失,一段时间后,该振动传播至某质点P,关于质点P振动的说法正确的是( )
A.振幅一定为A
B.周期一定为T
C.速度的最大值一定为v
D.开始振动的方向沿y轴向上或向下取决于它离波源的距离
2.一列简谐横波沿直线由A向B传播,A、B相距0.45 m,如图所示是A处质点的振动图象。当A处质点运动到波峰位置时,B处质点刚好到达平衡位置且向y轴正方向运动,这列波的波速可能是( )
A.4.5 m/s B.3.0 m/s
C.1.5 m/s D.0.7 m/s
3.一列简谐波在t时刻的波形如图中实线所示,此时刻质点M的运动方向向上,经过时间Δt的波形如图中虚线所示,若振动周期为T,则( )
A.Δt一定为 B.Δt可能为
C.Δt一定为 D.Δt可能为
4.简谐横波某时刻的波形如图所示,由此图可知( )
A.若质点A向下运动,则波是从左向右传播的
B.若质点B向上运动,则波是从左向右传播的
C.若波从右向左传播,则质点C向下运动
D.若波从右向左传播,则质点D向上运动
5.一列横波沿直线传播,在波的传播方向上有A、B两点,在t时刻A、B两点间形成的波形如图甲所示,在(t+3 s)时刻A、B两点间形成的波形如图乙所示,已知A、B两点间距离s=9 m,则以下说法中正确的是
A.若周期为4 s,波一定向右传播
B.若周期大于4 s,波可能向右传播
C.若波速为8.5 m/s,波一定向左传播
D.该波波速可能的最小值为0.5 m/s
6.一列简谐横波,在t=0时波形如图所示,P、Q两点的坐标分别为(-1,0)、(-7,0),波的传播方向由右向左,已知 t=0.7 s 时,P点第二次出现波峰,则( )
A.t=0.9 s时,Q点第一次出现波峰
B.t=1.2 s时,Q点第一次出现波峰
C.波源起振方向一定向上
D.质点Q位于波峰时,质点P位于波谷
7.如图所示,一列简谐横波在x轴上传播,图甲和图乙分别为x轴上a、b两质点的振动图象,且xab=6 m。下列判断正确的是( )
A.波长可能是8 m B.波长可能是10 m
C.波速可能是1.2 m/s D.波速可能是3.6 m/s
8.手持较长软绳端点O以周期T在竖直方向上做简谐运动,带动绳上的其他质点振动形成简谐波沿绳水平传播,如图.绳上有另一质点P,且O、P的平衡位置间距为L.t=0时,O位于最高点,P的位移恰好为零,速度方向竖直向上,下列判断正确的是( )
A.该简谐波是纵波
B.该简谐波的最大波长为2L
C.t=时,P在平衡位置上方
D.t=时,P的速度方向竖直向上
9.一列简谐横波沿x轴正方向传播,t时刻波形图如图10中的实线所示,此时波刚好传到P点,t+0.6 s时刻的波形如图中的虚线所示,a、b、c、P、Q是介质中的质点,则下列说法正确的是( )
A.这列波的波速可能为50 m/s
B.质点a在这段时间内通过的路程一定小于30 cm
C.质点c在这段时间内通过的路程可能为60 cm
D.若周期T=0.8 s,则在t+0.5 s时刻,质点b、P的位移相同
E.若周期T=0.8 s,从t+0.4 s时刻开始计时,则质点c的振动方程为x=0.1sin(πt) m
10. 如图,一列简谐横波沿x轴正方向传播,实线为t=0时的波形图,虚线为t=0.5 s时的波形图.已知该简谐波的周期大于0.5 s.关于该简谐波,下列说法正确的是( )
A.波长为2 m
B.波速为6 m/s
C.频率为1.5 Hz
D.t=1 s时,x=1 m处的质点处于波峰
E.t=2 s时,x=2 m处的质点经过平衡位置
计算题(共4小题,40分)
11.如图所示,简谐横波在t时刻的波形如实线所示,经过Δt=3 s,其波形如虚线所示。已知图中x1与x2相距1 m,波的周期为T,且2T<Δt<4T。则可能的最小波速为________ m/s,最小周期为________ s。
12.如图所示,实线为t1=0时刻的图象,虚线为t2=0.1 s时刻的波形,求:
(1)若波的传播方向为+x方向,周期T>0.1 s,波速多大;
(2)若波的传播方向为-x方向,周期T>0.1 s,波速多大;
(3)若波速为450 m/s,波沿什么方向传播。
13. 如图所示,实线是某时刻的波形图线,虚线是0.2 s后的波形图线。
(1)若波向左传播,求它传播的距离及最小距离;
(2)若波向右传播,求它的周期及最大周期;
(3)若波速为35 m/s,求波的传播方向。
14. 如图所示实线是一列简谐横波在t1=0时刻的波形,虚线是这列波在t2=0.5 s时刻的波形,这列波的周期T符合:3T
(2)若波向左传播,波速多大?
(3)若波速大小为74 m/s,波速方向如何?
答案及解析
1.解析:选AB 机械波将波源的振动形式和能量向外传递,对简谐波而言,介质中各振动质点的振幅和周期都与波源的相同,选项A、B正确;质点P的振动速度不是波的传播速度v,选项C错误;质点P开始振动的方向与波源开始振动的方向相同,与它们之间的距离无关,选项D错误。
2.解析:选A 如图所示,当A在波峰,B在平衡位置向上振动时,A、B两点间的距离与波长的关系为(n+)λ=0.45 m得:λ= m。由振动图象可知,T=0.4 s,所以波速v== m/s,当n=0时,v=4.5 m/s, n=1时,v=0.9 m/s。故A正确。
3.解析:选D 由M点的振动方向向上可判定波沿x轴负方向传播,可认为题图中虚线是由实线经过n+T(n=0,1,2,3…)的时间得到的,故Δt可能是T,D正确。
4.解析:选BD 如果波从左向右传播,则A、B两点都向上运动,C、D两点都向下运动,可知选项A错误,B正确;如果波从右向左传播,则A、B两点都向下运动,C、D两点都向上运动,可知选项C错误,D正确。
5.解析:选ACD 若波向右传播,3 s=T1,(n=0,1,2,……),T1= s;若波向左传播,3 s=T2,(n=0,1,2,……),T2= s;由于n是整数,当T=4 s时,符合T1通项,波向右传播。故A正确;由上分析,波向右传播的周期T≤4 s,故B错误;由题图可知波长λ=6 m,若波速为8.5 m/s,波传播的距离为x=vt=8.5×3 m=4λ,根据波形的平移,波一定向左传播。故C正确;波传播的最小距离为向左传播1.5 m,波速可能的最小值为v== m/s=0.5 m/s。故D正确。
6.解析:选ACD 由题图知波长λ=4 m,第二次波峰到达P点所需时间为T=0.7 s,得T=0.4 s,波速v= m/s=10 m/s。第一次波峰传播到Q点,传播距离Δx=2 m-(-7 m)=9 m,所需时间Δt= s=0.9 s,故选项A正确,B错误;P、Q两点间距6 m=λ,振动情况相反,选项D正确;波的最前方x=1 m 处的质点正处于平衡位置向上运动,由此可知波源起振方向向上,选项C正确。
7.解析:选AC 若波是从b向a传播,则a、b的振动相差n+个周期,距离相差n+个波长,则n+λ1=6 m,即λ1= m(n=0,1,2,3,…),同理,波从a向b传播时,λ2= m(n=0,1,2,…),由此知选项A正确,B错误;根据波速公式v=,波对应的传播速度分别为v1= m/s(n=0,1,2,…),v2= m/s(n=0,1,2,…),由此知选项C正确,D错误。
8.答案 C
解析 绳波中质点的振动方向与波的传播方向垂直,属于横波,故A错误;根据波形图和波的传播方向可知,位移恰好为零且速度方向竖直向上的质点与O点的距离应为L=λ,其中n=0、1、2……,波长λ=,可知当n=0时有波长的最大值,最大值为λm=4L,故B错误;0~内P由平衡位置振动到波峰,~内P由波峰回到平衡位置,可知t=时P在平衡位置上方向上振动,t=时P在平衡位置上方向下振动,故C正确,D错误.
9.解析 由波形图可知波长λ=40 m,且0.6 s=nT+T(n=0,1,2,…),解得周期T= s(n=0,1,2,…)。当n=0时,T=0.8 s,波速v==50 m/s,选项A正确;由传播方向沿x轴正方向可知质点a在t时刻向上运动,当n=0时,T=0.8 s,则质点a在这段时间内通过的路程小于30 cm,当n=1时,T= s,质点a在这段时间内通过的路程大于30 cm,选项B错误;若n=1,则T= s,波传播到c点所用时间为T,0.6 s=,质点c振动的时间为T-T=T,故在这段时间内质点c通过的路程则为6A=60 cm,选项C正确;若T=0.8 s,t+0.5 s时刻,质点b、P的位移均为负值,大小相等,选项D正确;若T=0.8 s,从t+0.4 s时刻开始计时,则质点c的振动方程为y=0.1cos(πt) m,选项E错误。
答案 ACD
10.答案 BCE
解析 由题图波形图可知,波长λ=4 m,故A错误;横波沿x轴正方向传播,实线为t=0时的波形图,虚线为t=0.5 s时的波形图,又该简谐波的周期大于0.5 s,则波传播的距离Δx=λ,T=0.5 s,故周期T= s,频率为1.5 Hz,波速v=λf=6 m/s,故B、C正确;t=1 s=T时,x=1 m处的质点处于波谷位置,故D错误;t=2 s=3T时,x=2 m处的质点正经过平衡位置向上运动,故E正确.
11.解析:由题图可知波长为λ=7 m。若波向右传播,则Δt=T+nT,故T=,结合题目可知n=2,3;若波向左传播,则Δt=T+mT,故T=,结合题目可知m=2,3。当波向右传播,且n=2时,周期T最大,为T= s,波速最小,最小波速为v== m/s=5 m/s。当波向左传播,且m=3时,周期最小,最小周期为T= s。
答案:5
12.解析:(1)若波沿+x方向传播,根据t与周期T的关系:由题图可直接读出波长λ=20 m。
t=0.1 s=(n+)T,周期T为:
T= s。
当周期T>0.1 s时,n=0,则
T=0.4 s,
则波速为:v==50 m/s。
(2)当波向-x传播时,0.1=(n+)T,T= s,当周期T>0.1 s时,n=0,则T= s
则波速为:v==150 m/s。
(3)x=vt=450×0.1 m=45 m=2λ+λ,波沿+x方向传播。
答案:(1)50 m/s (2)150 m/s
(3)沿+x方向传播
13.[解析] (1)由题图知,λ=4 m,若波向左传播,传播的距离可能值为Δx=nλ+λ=(4n+3)m(n=0,1,2,…)
最小距离为Δxmin=3 m。
(2)若波向右传播,Δx=nλ+λm,所用时间为Δt=n+T=0.2 s,故T= s(n=0,1,2,…),所以Tmax=0.8 s。
(3)Δx=v·Δt=35×0.2 m=7 m=(λ+3)m,所以波向左传播。
[答案] (1)Δx=(4n+3) m(n=0,1,2,…) 3 m (2)T= s(n=0,1,2,…) 0.8 s (3)波向左传播
14.答案 (1)54 m/s (2)58 m/s (3)波向左传播
解析 (1)由题目中波形图知λ=8 m,
波向右传播时,传播距离Δx满足
Δx=kλ+λ(k=0,1,2,3…)
则传播时间满足Δt=kT+T(k=0,1,2,3…)
由于3T
故Δt=3T+T,波速v=,
解得v=54 m/s.
(2)波向左传播时,传播距离Δx满足
Δx=kλ+λ(k=0,1,2,3…)
传播时间满足Δt=kT+T(k=0,1,2,3…)
由3T
解得v=58 m/s.
(3)波速大小为74 m/s时,波在Δt时间内传播的距离为Δx=vΔt=74×0.5 m=37 m=4λ+λ,所以波向左传播.
