11.3多边形及其内角和2021-2022学年度人教版八年级数学上册期中专题复习(Word版含解析)
文档属性
| 名称 | 11.3多边形及其内角和2021-2022学年度人教版八年级数学上册期中专题复习(Word版含解析) |

|
|
| 格式 | docx | ||
| 文件大小 | 220.8KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-10-20 00:00:00 | ||
图片预览



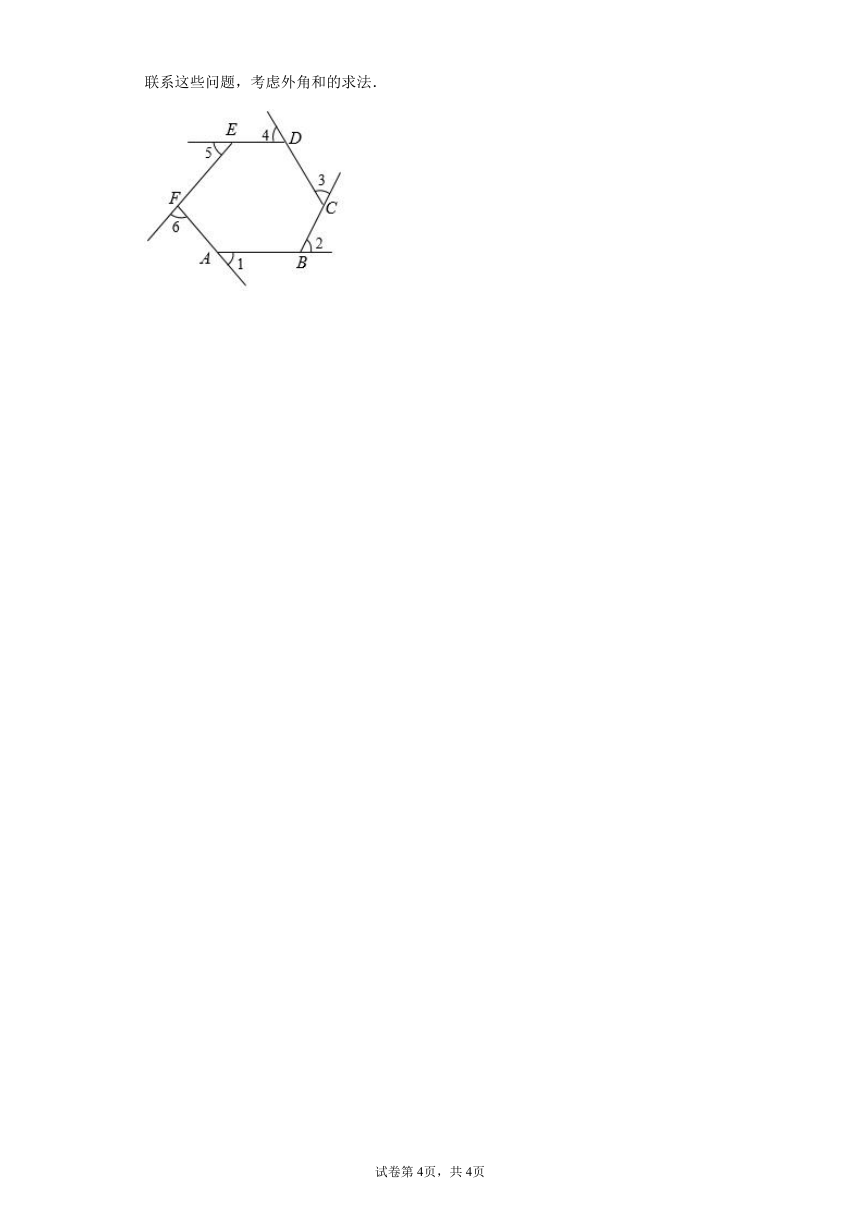
文档简介
11.3多边形及其内角和2021-2022学年度人教版八年级数学上册期中专题复习
一、选择题
1.要使如图所示的六边形木架不变形,则至少需要钉上木条的根数为( )
A.1 B.2 C.3 D.4
2.一个多边形截去一个角后,变成16边形,那么原来的多边形的边数为( )
A.15或16或17 B.15或17 C.16或17 D.16或17或18
3.一个八边形的所有对角线的条数是( )
A.5 B.20 C.22 D.18
4.若边形恰好有条对角线,则为( )
A.4 B.5 C.6 D.7
5.如果一个正多边形的一个外角是45°,则这个正多边形的边数是( )
A.8 B.7 C.6 D.5
6.在四边形ABCD中,设∠A=∠B=∠C=α,∠D=β( )
A.若α=60°,则β=60° B.若α=70°,则β=70°
C.若α=80°,则β=80° D.若α=90°,则β=90°
7.小明在计算某多边形的内角和时,由于马虎漏掉了一个角,结果得到970°,则原多边形是一个( )
A.七边形 B.八边形 C.九边形 D.十边形
8.如图,中,,将沿DE折叠,点A落在F处,则的度数为( )
A. B. C. D.
9.在矩形ABCD中,一条直线将矩形任意分为两部分,设这两部分图形的内角和分别为x、y,则x+y的和是( )
A.360°、540°、720° B.360°、540° C.540°、720° D.360°、720°
10.若多边形的内角和是,则此多边形的边数为( )
A.13 B.14 C.15 D.16
二、填空题
11.若一个多边形的内角和是,则该多边形的边数为______.
12.如果一个正多边形的内角和等于,那么这个正多边形的每一个外角的度数为___.
13.一个多边形的内角和它的外角和相等,则这个多边形是____边形.
14.如果一个多边形的内角和为1080°,那么从这个多边形的一个顶点出发的对角线有______条.
15.一个多边形的内角和比外角和的3倍多180°, 则它的边数是______.
16.如图,一辆汽车由A点出发向前行驶100米到B处,向左转45度,继续向前行驶同样的路程到C处,再向左转45度,按这样的行驶方法,回到A点总共行驶了______米.
17.如图,求∠A+∠B+∠C+∠D+∠E+∠F+∠G的度数为_______.
18.如图,一个多边形纸片按图示的剪法剪去一个内角后,得到一个内角和为 1800°的新多边形,则原多边形的边数为______________.
三、解答题
19.已知一个多边形的内角和是外角和的4倍,求边数.
20.如图,已知五边形ABCDE的各个内角都相等,AF∥CD交DB的延长线于点F,交DE的延长线于点G,若∠GDF=70°,求∠FBA的度数.
21.已知一个多边形的内角和与外角和的差为1080°.
(1)求这个多边形的边数.
(2)求此多边形的对角线条数.
22.看对话答题:
小梅说:这个多边形的内角和等于1125°
小红说:不对,你少加了一个角
问题:
(1) 他们在求几边形的内角和
(2) 少加的那个内角是多少度
23.填表:
多边形的边数 7 20
内角和
外角和
24.如图,在六边形的每个顶点处各取一个外角,这些外角的和叫做六边形的外角和.六边形的外角和等于多少?
分析:考虑以下问题:
(1)任何一个外角同与它相邻的内角有什么关系?
(2)六边形的6个外角加上与它们相邻的内角,所得总和是多少?
(3)上述总和与六边形的内角和 外角和有什么关系?
联系这些问题,考虑外角和的求法.
试卷第1页,共3页
试卷第1页,共3页
参考答案
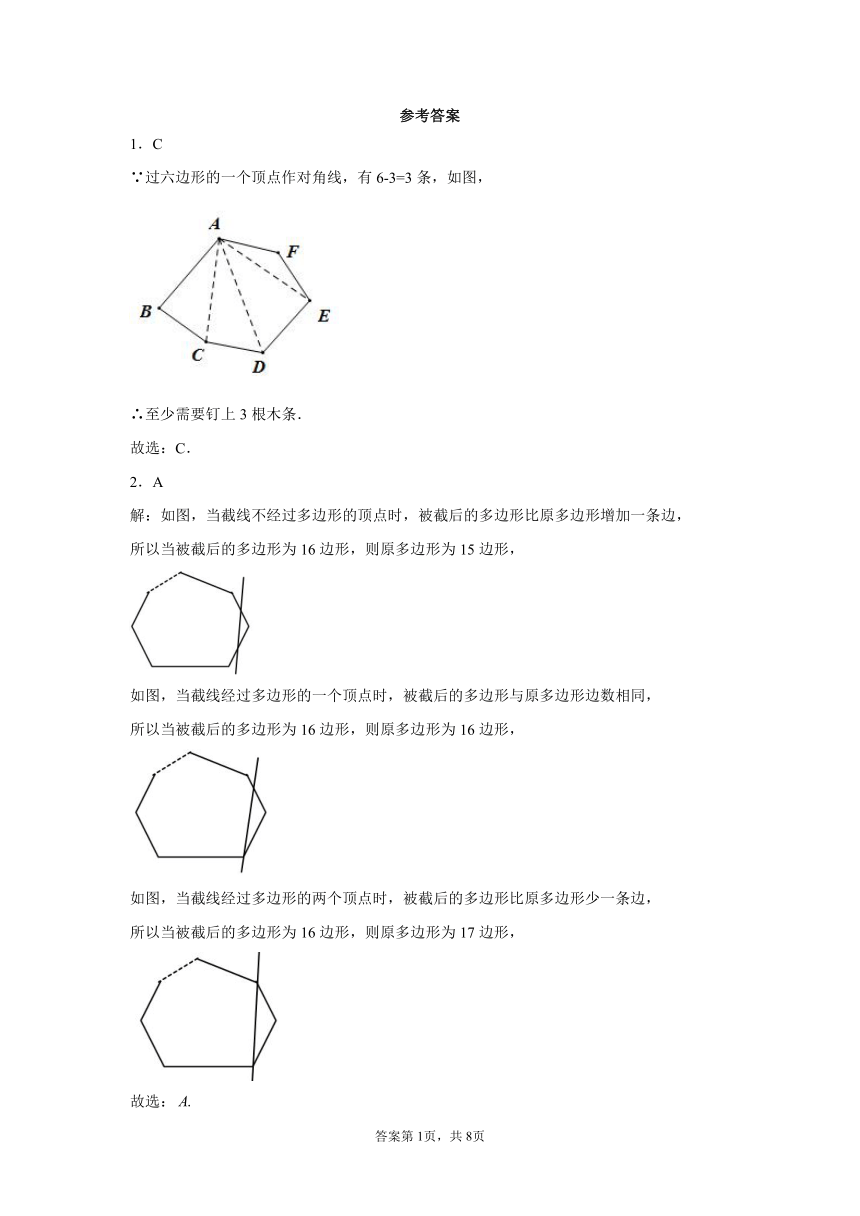
1.C
∵过六边形的一个顶点作对角线,有6-3=3条,如图,
∴至少需要钉上3根木条.
故选:C.
2.A
解:如图,当截线不经过多边形的顶点时,被截后的多边形比原多边形增加一条边,
所以当被截后的多边形为16边形,则原多边形为15边形,
如图,当截线经过多边形的一个顶点时,被截后的多边形与原多边形边数相同,
所以当被截后的多边形为16边形,则原多边形为16边形,
如图,当截线经过多边形的两个顶点时,被截后的多边形比原多边形少一条边,
所以当被截后的多边形为16边形,则原多边形为17边形,
故选:
3.B
解:×8×(8 3)
=×8×5
=20.
答:八边形所有对角线的条数是20.
故选:B.
4.D
解:依题意有:即
解得n=0(不合题意舍去)或n=7.
故选D.
5.A
多边形外角和为360°,且多边形为正多边形,
(条) .
故选:A.
6.D
解:在四边形ABCD中,∠A+∠B+∠C+∠D=360°,∠A=∠B=∠C=α,∠D=β,
A.若α=60°,则β=180°,故本选项不合题意;
B.若α=70°,则β=150°,故本选项不合题意;
C.若α=80°,则β=120°,故本选项不合题意;
D.若α=90°,则β=90°,故本选项符合题意;
故选:D.
7.B
解:设多边形的边数是n,
依题意有:
解得:,
∴则多边形的边数n=8;
故选B.
8.B
△DEF是由△DEA折叠而成的,
∠A = ∠F = 30°,
∠A+∠ADF+∠AEF+∠F = 360°,
∠ADF+∠AEF = 360°-∠A - ∠F = 300°,
∠BDF = 180°-∠ADF,
∠FEC= 180°-∠AEF,
∠FDB+ ∠FEC = 180°-∠ADF+180°-∠AEF
= 360°-(∠ADF+∠AEF)
= 360°- 300°
= 60°.
故选:B.
9.A
解:分三种情况:
①一条直线将矩形分为两个三角形,如图1所示:
则x+y=180°+180°=360°;
②一条直线将矩形分为一个三角形和一个四边形,如图2所示:
则x+y=180°+360°=540°;
③一条直线将矩形分为两个四边形,如图3所示:
则x+y=360°+360°=720°;
④一条直线将矩形分为1个三角形和1个五边形,如图4所示:
则;
综上所述,x+y的和是360°或540°或720°,
故选:A.
10.C
解:设内角和是2340°的多边形的边数是x,则180(x 2)=2340,
解得:x=15,
多边形的边数是15.
故选C.
11.5
解:设多边形的边数是n,则
(n﹣2) 180°=540°,
解得n=5.
故答案为:5.
12.36°
解:设此多边形为边形,
根据题意得:,
解得:,
这个正多边形的每一个外角等于:.
故答案为:.
13.4
解:设多边形的边数为n,根据题意
(n﹣2) 180°=360°,
解得n=4.
故答案为:4.
14.5
解:设多边形的边数为
由多边形内角和的公式可得,解得
多边形为八边形,有八个顶点,
从这个多边形的一个顶点出发的对角线有5条
故答案为5
15.9九
解:根据题意可得:
(n-2) 180°=3×360°+180°,
解得:n=9.
所以这个多边形的边数是9.
故答案为:9.
16.800
由题意得:360÷45=8
由于行驶的路程一样,所以汽车行驶的路程是一个正八边形的周长,且该正八边形的边长为100米,则汽车回到A点总共行驶的路程为:8×100=800(米).
故答案为:800.
17.540°
解:如图,
四边形ABCN中,∠A+∠B+∠C+∠1=360°,
四边形MNGF中,∠2+∠3+∠F+∠G=360°,
∵∠3=∠D+∠E,∠1+∠2=180°,
∴∠A+∠B+∠C+∠1+∠2+∠D+∠E+∠F+∠G=720°,
∴∠A+∠B+∠C+∠D+∠E+∠F+∠G=540°.
故答案是:540°.
18.11
解:设新多边形是n边形,由多边形内角和公式得:
(n﹣2)180°=1800°,
解得n=12,
原多边形是12﹣1=11,
故答案为:11.
19.10
解:设该多边形边数为,
则该多边形的内角和为,外角和为,
由题意,,
解得:,
∴该多边形的边数为10.
20.
解:对图形进行角标注,
多边形是正五边形,
多边形内角和为:,
,
,
,
,
,
.
21.
解:(1)设这个多边形的边数为,
由题意得,
解得.
答:这个多边形的边数为10.
(2)此多边形的对角线条数.
22.
解:(1)设少加的度数为x°,此多边形为n边形.
∵1125+x=(n-2)×180,
∴x=180(n-2)-1125,
∵0<x<180,
∴0<180(n-2)-1125<180,
∴8.25<n<9.25,
∴n=9;
∴他们在求九边形的内角和;
(2)∴x=180(n-2)-1125=135°.
∴少加的那个内角的度数是135°.
23.
解:若边数为7,则多边形的内角和为(7-2)×180°=5×180°;
若多边形的内角和为15×180°,则n-2=15,n=17;
若边数为20,则多边形的内角和为(20-2)×180°=18×180°;
若多边形的内角和为23×180°,则n-2=23,n=25,
∴填表如下:
多边形的边数 7 17 20 25
内角和 5×180° 15×180° 18×180° 23×180°
外角和 360° 360° 360° 360°
24.解:(1)六边形的任何一个外角加上与它相邻的内角都等于.
(2)六边形的6个外角加上与它们相邻的内角,所得总和等于.
(3)这个总和就是六边形的外角和加上内角和.所以外角和等于总和减去内角和,即外角和等于
.
多边形的外角和等于.
答案第1页,共2页
答案第1页,共2页
一、选择题
1.要使如图所示的六边形木架不变形,则至少需要钉上木条的根数为( )
A.1 B.2 C.3 D.4
2.一个多边形截去一个角后,变成16边形,那么原来的多边形的边数为( )
A.15或16或17 B.15或17 C.16或17 D.16或17或18
3.一个八边形的所有对角线的条数是( )
A.5 B.20 C.22 D.18
4.若边形恰好有条对角线,则为( )
A.4 B.5 C.6 D.7
5.如果一个正多边形的一个外角是45°,则这个正多边形的边数是( )
A.8 B.7 C.6 D.5
6.在四边形ABCD中,设∠A=∠B=∠C=α,∠D=β( )
A.若α=60°,则β=60° B.若α=70°,则β=70°
C.若α=80°,则β=80° D.若α=90°,则β=90°
7.小明在计算某多边形的内角和时,由于马虎漏掉了一个角,结果得到970°,则原多边形是一个( )
A.七边形 B.八边形 C.九边形 D.十边形
8.如图,中,,将沿DE折叠,点A落在F处,则的度数为( )
A. B. C. D.
9.在矩形ABCD中,一条直线将矩形任意分为两部分,设这两部分图形的内角和分别为x、y,则x+y的和是( )
A.360°、540°、720° B.360°、540° C.540°、720° D.360°、720°
10.若多边形的内角和是,则此多边形的边数为( )
A.13 B.14 C.15 D.16
二、填空题
11.若一个多边形的内角和是,则该多边形的边数为______.
12.如果一个正多边形的内角和等于,那么这个正多边形的每一个外角的度数为___.
13.一个多边形的内角和它的外角和相等,则这个多边形是____边形.
14.如果一个多边形的内角和为1080°,那么从这个多边形的一个顶点出发的对角线有______条.
15.一个多边形的内角和比外角和的3倍多180°, 则它的边数是______.
16.如图,一辆汽车由A点出发向前行驶100米到B处,向左转45度,继续向前行驶同样的路程到C处,再向左转45度,按这样的行驶方法,回到A点总共行驶了______米.
17.如图,求∠A+∠B+∠C+∠D+∠E+∠F+∠G的度数为_______.
18.如图,一个多边形纸片按图示的剪法剪去一个内角后,得到一个内角和为 1800°的新多边形,则原多边形的边数为______________.
三、解答题
19.已知一个多边形的内角和是外角和的4倍,求边数.
20.如图,已知五边形ABCDE的各个内角都相等,AF∥CD交DB的延长线于点F,交DE的延长线于点G,若∠GDF=70°,求∠FBA的度数.
21.已知一个多边形的内角和与外角和的差为1080°.
(1)求这个多边形的边数.
(2)求此多边形的对角线条数.
22.看对话答题:
小梅说:这个多边形的内角和等于1125°
小红说:不对,你少加了一个角
问题:
(1) 他们在求几边形的内角和
(2) 少加的那个内角是多少度
23.填表:
多边形的边数 7 20
内角和
外角和
24.如图,在六边形的每个顶点处各取一个外角,这些外角的和叫做六边形的外角和.六边形的外角和等于多少?
分析:考虑以下问题:
(1)任何一个外角同与它相邻的内角有什么关系?
(2)六边形的6个外角加上与它们相邻的内角,所得总和是多少?
(3)上述总和与六边形的内角和 外角和有什么关系?
联系这些问题,考虑外角和的求法.
试卷第1页,共3页
试卷第1页,共3页
参考答案
1.C
∵过六边形的一个顶点作对角线,有6-3=3条,如图,
∴至少需要钉上3根木条.
故选:C.
2.A
解:如图,当截线不经过多边形的顶点时,被截后的多边形比原多边形增加一条边,
所以当被截后的多边形为16边形,则原多边形为15边形,
如图,当截线经过多边形的一个顶点时,被截后的多边形与原多边形边数相同,
所以当被截后的多边形为16边形,则原多边形为16边形,
如图,当截线经过多边形的两个顶点时,被截后的多边形比原多边形少一条边,
所以当被截后的多边形为16边形,则原多边形为17边形,
故选:
3.B
解:×8×(8 3)
=×8×5
=20.
答:八边形所有对角线的条数是20.
故选:B.
4.D
解:依题意有:即
解得n=0(不合题意舍去)或n=7.
故选D.
5.A
多边形外角和为360°,且多边形为正多边形,
(条) .
故选:A.
6.D
解:在四边形ABCD中,∠A+∠B+∠C+∠D=360°,∠A=∠B=∠C=α,∠D=β,
A.若α=60°,则β=180°,故本选项不合题意;
B.若α=70°,则β=150°,故本选项不合题意;
C.若α=80°,则β=120°,故本选项不合题意;
D.若α=90°,则β=90°,故本选项符合题意;
故选:D.
7.B
解:设多边形的边数是n,
依题意有:
解得:,
∴则多边形的边数n=8;
故选B.
8.B
△DEF是由△DEA折叠而成的,
∠A = ∠F = 30°,
∠A+∠ADF+∠AEF+∠F = 360°,
∠ADF+∠AEF = 360°-∠A - ∠F = 300°,
∠BDF = 180°-∠ADF,
∠FEC= 180°-∠AEF,
∠FDB+ ∠FEC = 180°-∠ADF+180°-∠AEF
= 360°-(∠ADF+∠AEF)
= 360°- 300°
= 60°.
故选:B.
9.A
解:分三种情况:
①一条直线将矩形分为两个三角形,如图1所示:
则x+y=180°+180°=360°;
②一条直线将矩形分为一个三角形和一个四边形,如图2所示:
则x+y=180°+360°=540°;
③一条直线将矩形分为两个四边形,如图3所示:
则x+y=360°+360°=720°;
④一条直线将矩形分为1个三角形和1个五边形,如图4所示:
则;
综上所述,x+y的和是360°或540°或720°,
故选:A.
10.C
解:设内角和是2340°的多边形的边数是x,则180(x 2)=2340,
解得:x=15,
多边形的边数是15.
故选C.
11.5
解:设多边形的边数是n,则
(n﹣2) 180°=540°,
解得n=5.
故答案为:5.
12.36°
解:设此多边形为边形,
根据题意得:,
解得:,
这个正多边形的每一个外角等于:.
故答案为:.
13.4
解:设多边形的边数为n,根据题意
(n﹣2) 180°=360°,
解得n=4.
故答案为:4.
14.5
解:设多边形的边数为
由多边形内角和的公式可得,解得
多边形为八边形,有八个顶点,
从这个多边形的一个顶点出发的对角线有5条
故答案为5
15.9九
解:根据题意可得:
(n-2) 180°=3×360°+180°,
解得:n=9.
所以这个多边形的边数是9.
故答案为:9.
16.800
由题意得:360÷45=8
由于行驶的路程一样,所以汽车行驶的路程是一个正八边形的周长,且该正八边形的边长为100米,则汽车回到A点总共行驶的路程为:8×100=800(米).
故答案为:800.
17.540°
解:如图,
四边形ABCN中,∠A+∠B+∠C+∠1=360°,
四边形MNGF中,∠2+∠3+∠F+∠G=360°,
∵∠3=∠D+∠E,∠1+∠2=180°,
∴∠A+∠B+∠C+∠1+∠2+∠D+∠E+∠F+∠G=720°,
∴∠A+∠B+∠C+∠D+∠E+∠F+∠G=540°.
故答案是:540°.
18.11
解:设新多边形是n边形,由多边形内角和公式得:
(n﹣2)180°=1800°,
解得n=12,
原多边形是12﹣1=11,
故答案为:11.
19.10
解:设该多边形边数为,
则该多边形的内角和为,外角和为,
由题意,,
解得:,
∴该多边形的边数为10.
20.
解:对图形进行角标注,
多边形是正五边形,
多边形内角和为:,
,
,
,
,
,
.
21.
解:(1)设这个多边形的边数为,
由题意得,
解得.
答:这个多边形的边数为10.
(2)此多边形的对角线条数.
22.
解:(1)设少加的度数为x°,此多边形为n边形.
∵1125+x=(n-2)×180,
∴x=180(n-2)-1125,
∵0<x<180,
∴0<180(n-2)-1125<180,
∴8.25<n<9.25,
∴n=9;
∴他们在求九边形的内角和;
(2)∴x=180(n-2)-1125=135°.
∴少加的那个内角的度数是135°.
23.
解:若边数为7,则多边形的内角和为(7-2)×180°=5×180°;
若多边形的内角和为15×180°,则n-2=15,n=17;
若边数为20,则多边形的内角和为(20-2)×180°=18×180°;
若多边形的内角和为23×180°,则n-2=23,n=25,
∴填表如下:
多边形的边数 7 17 20 25
内角和 5×180° 15×180° 18×180° 23×180°
外角和 360° 360° 360° 360°
24.解:(1)六边形的任何一个外角加上与它相邻的内角都等于.
(2)六边形的6个外角加上与它们相邻的内角,所得总和等于.
(3)这个总和就是六边形的外角和加上内角和.所以外角和等于总和减去内角和,即外角和等于
.
多边形的外角和等于.
答案第1页,共2页
答案第1页,共2页
