青岛版 2021-2022学年九年级数学上册3.3圆周角 同步达标测评 (word版含解析)
文档属性
| 名称 | 青岛版 2021-2022学年九年级数学上册3.3圆周角 同步达标测评 (word版含解析) |  | |
| 格式 | doc | ||
| 文件大小 | 240.7KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 青岛版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-10-20 18:13:19 | ||
图片预览



文档简介
2021-2022学年青岛版九年级数学上册《3.3圆周角》同步达标测评(附答案)
一.选择题(共6小题,满分24分)
1.在圆中,弦AB、CD相交于E.若∠ADC=46°,∠BCD=33°,则∠DEB等于( )
A.13° B.79° C.38.5° D.101°
2.如图所示,AD是△ABC的高,AE是⊙O的直径,A,B,C三点都在圆上,∠DAC=30°,则∠BAE为( )
A.10° B.30° C.20° D.18°
3.如图,△ABC内接于⊙O,AC是⊙的直径,∠ACB=50°,点D是⊙O上一点,则∠D=( )
A.50° B.40° C.30° D.20°
4.如图,AB是⊙O的直径,点D在⊙O上,∠AOD=130°,BC∥OD交⊙O于C,则∠A等于( )
A.50° B.40° C.30° D.20°
5.若四边形ABCD是⊙O的内接四边形,则∠A:∠B:∠C:∠D的值可能是( )
A.2:3:4:5 B.1:2:3:4 C.2:5:4:1 D.4:3:3:2
6.在⊙O中,弦AB和CD相交于点P,若PA=4,PB=7,CD=12,则以PC、PD的长为根的一元二次方程为( )
A.x2+12x+28=0 B.x2﹣12x+28=0
C.x2﹣11x+12=0 D.x2+11x+12=0
二.填空题(共10小题,满分40分)
7.已知如图,四边形ABCD内接于⊙O,若∠A=60°,则∠DCE= .
8.已知圆的两条弦AB,CD交于P点,且PA=PB=4,PD=2,则PC= .
9.已知圆的一条弦AB把圆分成1:4的两部分,则此弦所对的圆周角等于 .
10.如图,AB是⊙O的直径,BC是弦,OD⊥BC,垂足为D,已知OD=5,则弦AC= .
11.如图,AB是⊙O的直径,CD是⊙O的弦,AB,CD的延长线交于E,若AB=2DE,∠E=18°,∠C= ,∠AOC= .
12.如图,点A、B、C、D在同一个圆上,四边形ABCD的对角线把4个内角分成8个角,在这8个角中,有几对相等的角?请把它们分别表示出来: .
13.如图所示,在⊙O中,弦AB,CD相交于E,且∠BEC=78°,∠BAC=36°,则∠DOA= 度.
14.已知,如图,∠BAC的对角∠BAD=100°,则∠BOC= 度.
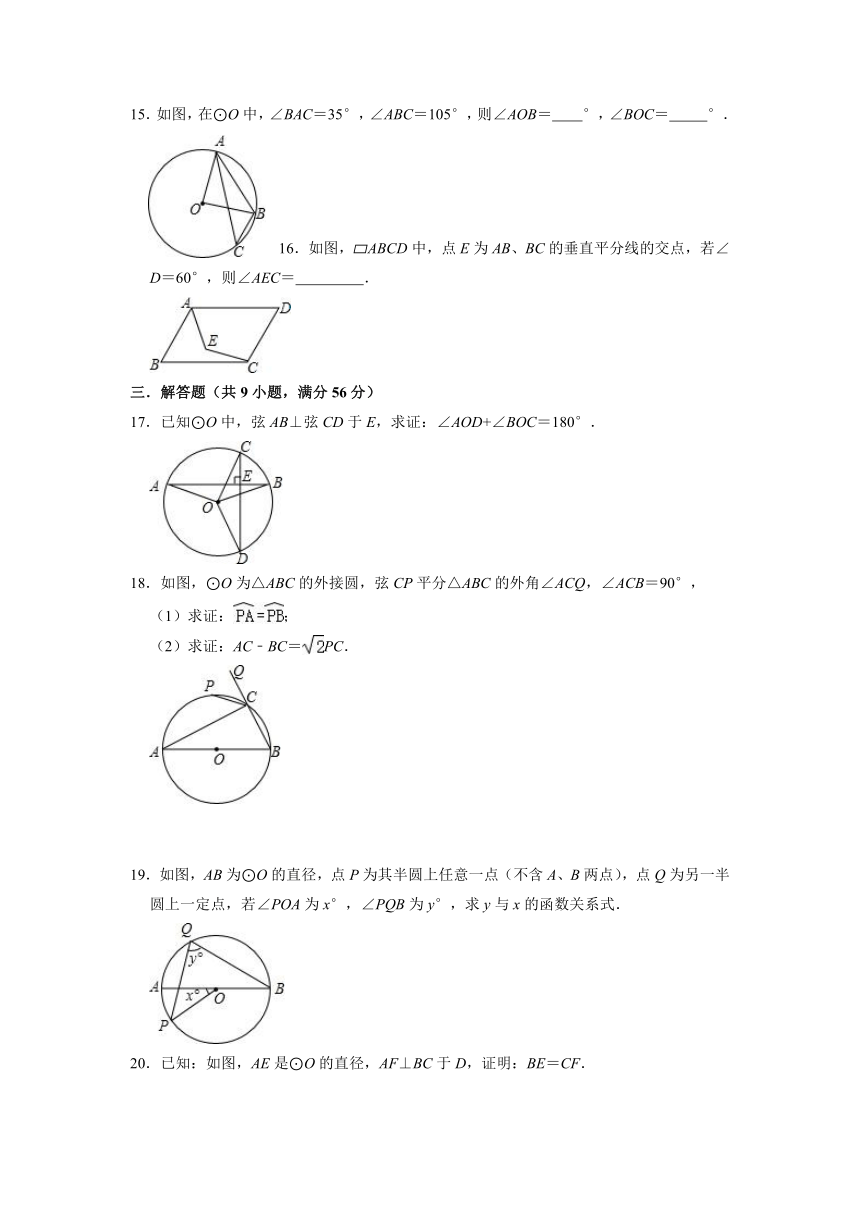
15.如图,在⊙O中,∠BAC=35°,∠ABC=105°,则∠AOB= °,∠BOC= °.
16.如图, ABCD中,点E为AB、BC的垂直平分线的交点,若∠D=60°,则∠AEC= .
三.解答题(共9小题,满分56分)
17.已知⊙O中,弦AB⊥弦CD于E,求证:∠AOD+∠BOC=180°.
18.如图,⊙O为△ABC的外接圆,弦CP平分△ABC的外角∠ACQ,∠ACB=90°,
(1)求证:;
(2)求证:AC﹣BC=PC.
19.如图,AB为⊙O的直径,点P为其半圆上任意一点(不含A、B两点),点Q为另一半圆上一定点,若∠POA为x°,∠PQB为y°,求y与x的函数关系式.
20.已知:如图,AE是⊙O的直径,AF⊥BC于D,证明:BE=CF.
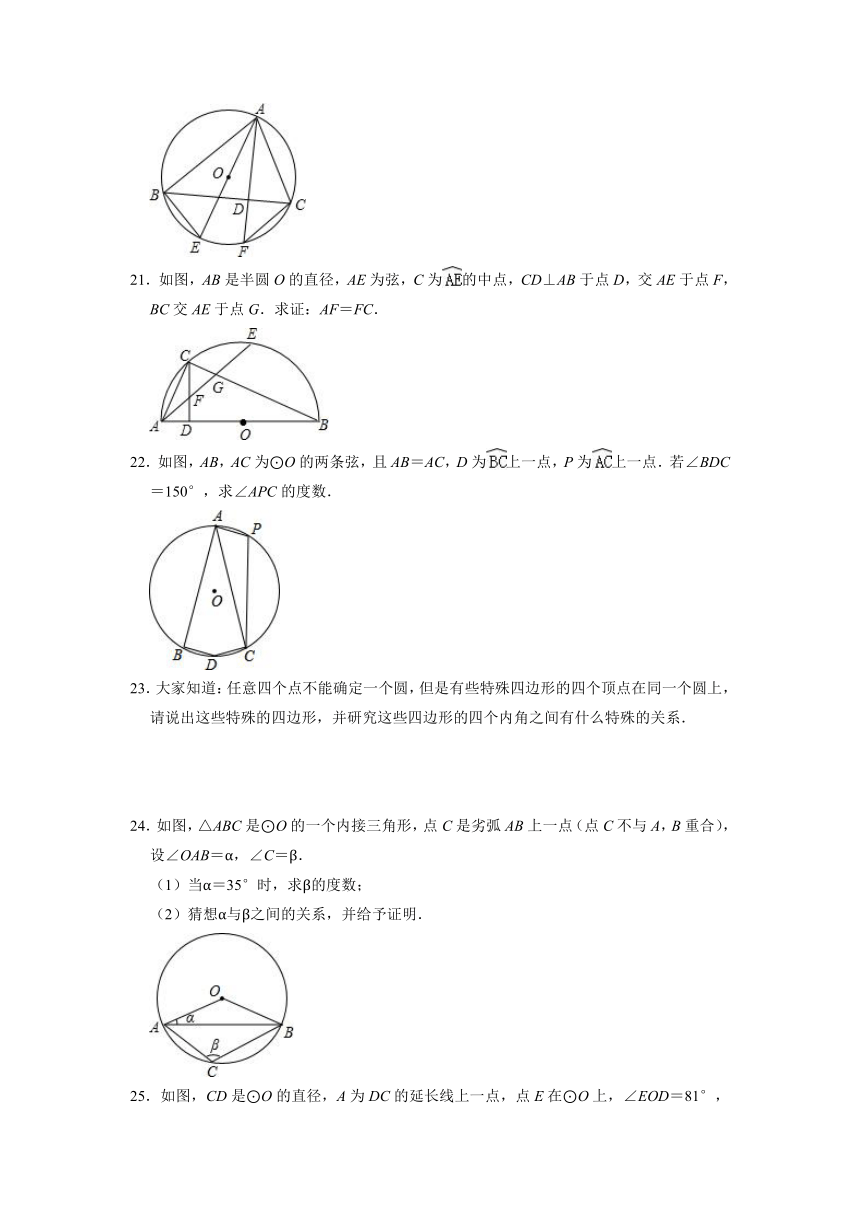
21.如图,AB是半圆O的直径,AE为弦,C为的中点,CD⊥AB于点D,交AE于点F,BC交AE于点G.求证:AF=FC.
22.如图,AB,AC为⊙O的两条弦,且AB=AC,D为上一点,P为上一点.若∠BDC=150°,求∠APC的度数.
23.大家知道:任意四个点不能确定一个圆,但是有些特殊四边形的四个顶点在同一个圆上,请说出这些特殊的四边形,并研究这些四边形的四个内角之间有什么特殊的关系.
24.如图,△ABC是⊙O的一个内接三角形,点C是劣弧AB上一点(点C不与A,B重合),设∠OAB=α,∠C=β.
(1)当α=35°时,求β的度数;
(2)猜想α与β之间的关系,并给予证明.
25.如图,CD是⊙O的直径,A为DC的延长线上一点,点E在⊙O上,∠EOD=81°,AE交⊙O于B,且AB=OC,求∠A的度数.
参考答案
一.选择题(共6小题,满分24分)
1.解:∵∠B与∠ADC是对的圆周角,
∴∠B=∠ADC=46°,
∵∠BCD=33°,
∴∠DEB=∠BCD+∠B=79°.
故选:B.
2.解:连接BE,
∵AE是⊙O的直径,
∴∠ABE=90°,
∴∠BAE=90°﹣∠E,
∵AD是△ABC的高,
∴∠ADC=90°,
∴∠DAC=90°﹣∠C,
∵∠E=∠C,
∴∠BAE=∠DAC=30°.
故选:B.
3.解:∵AC是⊙O的直径,
∴∠ABC=90°,
∵∠ACB=50°,
∴∠A=90°﹣∠ACB=40°,
∴∠D=∠A=40°.
故选:B.
4.解:∵∠AOD=130°,
∴∠BOD=50°;
∵BC∥OD,
∴∠B=∠BOD=50°;
∵AB是⊙O的直径,
∴∠ACB=90°;
∴∠A=90°﹣∠B=40°.
故选:B.
5.解:∵圆的内接四边形对角互补,
∴∠A+∠C=∠B+∠D=180°,
∴∠A:∠B:∠C:∠D的可能的值是2:5:4:1.
故选:C.
6.解:设PC=x,则PD=12﹣x,
由相交弦定理得:PA PB=PC PD,
∵PA=4,PB=7,
∴4×7=x(12﹣x)=PC PD,
PC+PD=x+12﹣x=12,
即以PC、PD为根的一元二次方程为:x2﹣12x+28=0.
故选:B.
二.填空题(共10小题,满分40分)
7.解:∵四边形ABCD是圆内接四边形,
∴∠A+∠BCD=180°,
∵∠BCD+∠DCE=180°,
∴∠DCE=∠A.
∵∠A=60°,
∴∠DCE=60°.
故答案为:60°.
8.解:根据题意得PA PB=PC PD,
即4×4=2PC,
所以PC=8.
故答案为8.
9.解:∵弦AB把⊙O分成1:4两部分,
∴∠AOB=×360°=72°,
∴∠ACB=∠AOB=36°,
∵四边形ADBC是⊙O的内接四边形,
∴∠ADB=180°﹣∠ACB=144°.
∴这条弦所对的圆周角的度数是:36°或144°,
故答案为:36°或144°.
10.解:∵OD⊥BC,
∴D为弦BC的中点,
∵点O为AB的中点,D为弦BC的中点,
∴OD是△ABC的中位线,
∴BC=2OD=10.
故答案为:10.
11.解:连接OD,
∵AB=2DE,
∴OD=DE,
∴∠E=∠EOD,
在△EDO中,∠ODC=∠E+∠EOD=36°,
∵OC=OD,
∴∠OCD=∠ODC=36°,
在△CEO中,∠AOC=∠E+∠OCD=18°+36°=54°.
故答案为:36°;54°.
12.解:有4对.
分别是:∠1=∠2,∠3=∠4,∠5=∠6,∠7=∠8.
故答案为:∠1=∠2,∠3=∠4,∠5=∠6,∠7=∠8.
13.解:∵∠C=∠BEC﹣∠BAC=78°﹣36°=42°,
∴∠DOA=2∠C=84°.
14.解:∵∠BAD=100°
∴∠BAC=180°﹣∠BAD=80°
∴∠BOC=2∠BAC=160°.
15.解:连接OC,如图,
∵∠BAC=35°,∠ABC=105°,
∴∠ACB=180°﹣∠BAC﹣∠ABC=180°﹣35°﹣105°=40°,
又∵∠ACB=∠AOB,
∴∠AOB=2×40°=80°;
又∵∠BAC=∠BOC,而∠BAC=35°,
∴∠BOC=2×35°=70°.
故答案为:80°,70°.
16.解:连接BE,
∵点E为AB、BC的垂直平分线的交点,
∴AE=BE,BE=CE,
∴AE=BE=CE,
∴点A,B,C在以E为圆心,AE为半径的圆上,
∵四边形ABCD是平行四边形,
∴∠B=∠D=60°,
∴∠AEC=2∠B=120°.
故答案为:120°.
三.解答题(共9小题,满分56分)
17.解:连接AC,BD,
由圆周角定理得:∠AOD=2∠ABD,∠BOC=2∠CDB,
∵弦AB⊥弦CD
∴∠ABD+∠BDC=90°,
∴∠AOD+∠BOC=2∠ABD+2∠BDC=2(∠ABD+∠CDB)=2×90°=180°
18.证明:(1)连接PA、PB,如图,
∵弦CP平分△ABC的外角∠ACQ,∠ACB=90°,
∴∠ACP=45°,AB为⊙O的直径,
∴∠APB=90°,
∴∠PAB=45°,
∴;
(2)作PD⊥PC交AC于D点,如图,
则△PDC为等腰直角三角形,
∴DC=PC,
∵=,
∴PA=PB,
∵∠PDC=45°,
∴∠PDA=135°,
而∠PCB=∠PCA+∠ACB=135°,
∴∠PDC=∠PCB,
∵∠PAD=∠PBC,
∴△PDA≌△PCB,
∴AD=BC,
∴AC﹣BC=AC﹣AD=DC=PC.
19.解:∵∠BOP=2∠BQP=2y°,
∵AB为⊙O的直径,
∴∠AOP+∠BOP=180°,
∴x+2y=180,
∴y=90﹣x,且0<x<180.
20.证明:∵AE是⊙O的直径,
∴∠ABE=90°,
∴∠E+∠BAE=90°,
∵AF⊥BC于D,
∴∠FAC+∠ACB=90°,
∵∠E=∠ACB,
∴∠BAE=∠FAC,
∴弧BE=弧CF,
∴BE=CF.
21.证明:∵点C是弧AE的中点,
∴∠B=∠CAE,
∵AB是⊙O的直径,
∴∠ACB=90°,
即∠ACF+∠BCD=90°,
∵CD⊥AB,
∴∠B+∠BCD=90°,
又∠ACF+∠BCD=90°,
∴∠B=∠ACF
∴∠B=∠CAF=∠ACF,
∴AF=CF.
22.解:在圆内接四边形ABCD中,∠BAC=180°﹣∠BDC=180°﹣150°=30°,
则弧BC的度数是60°,
又∵AB=AC,
∴弧AB=弧AC=150°,
∴弧ABC是210°,
∴∠APC=×210°=105°.
23.解:∵矩形、正方形的对角线相等且互相平分,
∴四个顶点到对角线交点距离相等,
∴矩形、正方形的四个顶点可在同一个圆上;
四个顶点在同一个圆上的四边形的对角互补.
24.解:(1)在优弧AB上取一点D,连接DA、DB,如图,
∵∠α=35°,
∴∠AOB=180°﹣∠OAB﹣∠OBA=180°﹣2×35°=110°,
∴∠D=∠AOB=55°,
∴∠ACB=180°﹣∠D=125°,
即β的度数为125°;
(2)∠ACB=90°+α.理由如下:
∵∠AOB=180°﹣2∠α,
∴∠D=∠AOB=(180°﹣2∠α)=90°﹣α,
∴∠ACB=180°﹣∠D=180°﹣(90°﹣α)=90°+α.
解:连OB,如图,
∵AB=OC,OB=OC,
∴AB=BO,
∴∠A=∠2,
而∠1=∠A+∠2,
∴∠1=2∠A,
∵OB=OE,
∴∠1=∠E,
∴∠E=2∠A,
而∠EOD=∠A+∠E=81°,
∴3∠A=81°,
所以∠A=27°.
一.选择题(共6小题,满分24分)
1.在圆中,弦AB、CD相交于E.若∠ADC=46°,∠BCD=33°,则∠DEB等于( )
A.13° B.79° C.38.5° D.101°
2.如图所示,AD是△ABC的高,AE是⊙O的直径,A,B,C三点都在圆上,∠DAC=30°,则∠BAE为( )
A.10° B.30° C.20° D.18°
3.如图,△ABC内接于⊙O,AC是⊙的直径,∠ACB=50°,点D是⊙O上一点,则∠D=( )
A.50° B.40° C.30° D.20°
4.如图,AB是⊙O的直径,点D在⊙O上,∠AOD=130°,BC∥OD交⊙O于C,则∠A等于( )
A.50° B.40° C.30° D.20°
5.若四边形ABCD是⊙O的内接四边形,则∠A:∠B:∠C:∠D的值可能是( )
A.2:3:4:5 B.1:2:3:4 C.2:5:4:1 D.4:3:3:2
6.在⊙O中,弦AB和CD相交于点P,若PA=4,PB=7,CD=12,则以PC、PD的长为根的一元二次方程为( )
A.x2+12x+28=0 B.x2﹣12x+28=0
C.x2﹣11x+12=0 D.x2+11x+12=0
二.填空题(共10小题,满分40分)
7.已知如图,四边形ABCD内接于⊙O,若∠A=60°,则∠DCE= .
8.已知圆的两条弦AB,CD交于P点,且PA=PB=4,PD=2,则PC= .
9.已知圆的一条弦AB把圆分成1:4的两部分,则此弦所对的圆周角等于 .
10.如图,AB是⊙O的直径,BC是弦,OD⊥BC,垂足为D,已知OD=5,则弦AC= .
11.如图,AB是⊙O的直径,CD是⊙O的弦,AB,CD的延长线交于E,若AB=2DE,∠E=18°,∠C= ,∠AOC= .
12.如图,点A、B、C、D在同一个圆上,四边形ABCD的对角线把4个内角分成8个角,在这8个角中,有几对相等的角?请把它们分别表示出来: .
13.如图所示,在⊙O中,弦AB,CD相交于E,且∠BEC=78°,∠BAC=36°,则∠DOA= 度.
14.已知,如图,∠BAC的对角∠BAD=100°,则∠BOC= 度.
15.如图,在⊙O中,∠BAC=35°,∠ABC=105°,则∠AOB= °,∠BOC= °.
16.如图, ABCD中,点E为AB、BC的垂直平分线的交点,若∠D=60°,则∠AEC= .
三.解答题(共9小题,满分56分)
17.已知⊙O中,弦AB⊥弦CD于E,求证:∠AOD+∠BOC=180°.
18.如图,⊙O为△ABC的外接圆,弦CP平分△ABC的外角∠ACQ,∠ACB=90°,
(1)求证:;
(2)求证:AC﹣BC=PC.
19.如图,AB为⊙O的直径,点P为其半圆上任意一点(不含A、B两点),点Q为另一半圆上一定点,若∠POA为x°,∠PQB为y°,求y与x的函数关系式.
20.已知:如图,AE是⊙O的直径,AF⊥BC于D,证明:BE=CF.
21.如图,AB是半圆O的直径,AE为弦,C为的中点,CD⊥AB于点D,交AE于点F,BC交AE于点G.求证:AF=FC.
22.如图,AB,AC为⊙O的两条弦,且AB=AC,D为上一点,P为上一点.若∠BDC=150°,求∠APC的度数.
23.大家知道:任意四个点不能确定一个圆,但是有些特殊四边形的四个顶点在同一个圆上,请说出这些特殊的四边形,并研究这些四边形的四个内角之间有什么特殊的关系.
24.如图,△ABC是⊙O的一个内接三角形,点C是劣弧AB上一点(点C不与A,B重合),设∠OAB=α,∠C=β.
(1)当α=35°时,求β的度数;
(2)猜想α与β之间的关系,并给予证明.
25.如图,CD是⊙O的直径,A为DC的延长线上一点,点E在⊙O上,∠EOD=81°,AE交⊙O于B,且AB=OC,求∠A的度数.
参考答案
一.选择题(共6小题,满分24分)
1.解:∵∠B与∠ADC是对的圆周角,
∴∠B=∠ADC=46°,
∵∠BCD=33°,
∴∠DEB=∠BCD+∠B=79°.
故选:B.
2.解:连接BE,
∵AE是⊙O的直径,
∴∠ABE=90°,
∴∠BAE=90°﹣∠E,
∵AD是△ABC的高,
∴∠ADC=90°,
∴∠DAC=90°﹣∠C,
∵∠E=∠C,
∴∠BAE=∠DAC=30°.
故选:B.
3.解:∵AC是⊙O的直径,
∴∠ABC=90°,
∵∠ACB=50°,
∴∠A=90°﹣∠ACB=40°,
∴∠D=∠A=40°.
故选:B.
4.解:∵∠AOD=130°,
∴∠BOD=50°;
∵BC∥OD,
∴∠B=∠BOD=50°;
∵AB是⊙O的直径,
∴∠ACB=90°;
∴∠A=90°﹣∠B=40°.
故选:B.
5.解:∵圆的内接四边形对角互补,
∴∠A+∠C=∠B+∠D=180°,
∴∠A:∠B:∠C:∠D的可能的值是2:5:4:1.
故选:C.
6.解:设PC=x,则PD=12﹣x,
由相交弦定理得:PA PB=PC PD,
∵PA=4,PB=7,
∴4×7=x(12﹣x)=PC PD,
PC+PD=x+12﹣x=12,
即以PC、PD为根的一元二次方程为:x2﹣12x+28=0.
故选:B.
二.填空题(共10小题,满分40分)
7.解:∵四边形ABCD是圆内接四边形,
∴∠A+∠BCD=180°,
∵∠BCD+∠DCE=180°,
∴∠DCE=∠A.
∵∠A=60°,
∴∠DCE=60°.
故答案为:60°.
8.解:根据题意得PA PB=PC PD,
即4×4=2PC,
所以PC=8.
故答案为8.
9.解:∵弦AB把⊙O分成1:4两部分,
∴∠AOB=×360°=72°,
∴∠ACB=∠AOB=36°,
∵四边形ADBC是⊙O的内接四边形,
∴∠ADB=180°﹣∠ACB=144°.
∴这条弦所对的圆周角的度数是:36°或144°,
故答案为:36°或144°.
10.解:∵OD⊥BC,
∴D为弦BC的中点,
∵点O为AB的中点,D为弦BC的中点,
∴OD是△ABC的中位线,
∴BC=2OD=10.
故答案为:10.
11.解:连接OD,
∵AB=2DE,
∴OD=DE,
∴∠E=∠EOD,
在△EDO中,∠ODC=∠E+∠EOD=36°,
∵OC=OD,
∴∠OCD=∠ODC=36°,
在△CEO中,∠AOC=∠E+∠OCD=18°+36°=54°.
故答案为:36°;54°.
12.解:有4对.
分别是:∠1=∠2,∠3=∠4,∠5=∠6,∠7=∠8.
故答案为:∠1=∠2,∠3=∠4,∠5=∠6,∠7=∠8.
13.解:∵∠C=∠BEC﹣∠BAC=78°﹣36°=42°,
∴∠DOA=2∠C=84°.
14.解:∵∠BAD=100°
∴∠BAC=180°﹣∠BAD=80°
∴∠BOC=2∠BAC=160°.
15.解:连接OC,如图,
∵∠BAC=35°,∠ABC=105°,
∴∠ACB=180°﹣∠BAC﹣∠ABC=180°﹣35°﹣105°=40°,
又∵∠ACB=∠AOB,
∴∠AOB=2×40°=80°;
又∵∠BAC=∠BOC,而∠BAC=35°,
∴∠BOC=2×35°=70°.
故答案为:80°,70°.
16.解:连接BE,
∵点E为AB、BC的垂直平分线的交点,
∴AE=BE,BE=CE,
∴AE=BE=CE,
∴点A,B,C在以E为圆心,AE为半径的圆上,
∵四边形ABCD是平行四边形,
∴∠B=∠D=60°,
∴∠AEC=2∠B=120°.
故答案为:120°.
三.解答题(共9小题,满分56分)
17.解:连接AC,BD,
由圆周角定理得:∠AOD=2∠ABD,∠BOC=2∠CDB,
∵弦AB⊥弦CD
∴∠ABD+∠BDC=90°,
∴∠AOD+∠BOC=2∠ABD+2∠BDC=2(∠ABD+∠CDB)=2×90°=180°
18.证明:(1)连接PA、PB,如图,
∵弦CP平分△ABC的外角∠ACQ,∠ACB=90°,
∴∠ACP=45°,AB为⊙O的直径,
∴∠APB=90°,
∴∠PAB=45°,
∴;
(2)作PD⊥PC交AC于D点,如图,
则△PDC为等腰直角三角形,
∴DC=PC,
∵=,
∴PA=PB,
∵∠PDC=45°,
∴∠PDA=135°,
而∠PCB=∠PCA+∠ACB=135°,
∴∠PDC=∠PCB,
∵∠PAD=∠PBC,
∴△PDA≌△PCB,
∴AD=BC,
∴AC﹣BC=AC﹣AD=DC=PC.
19.解:∵∠BOP=2∠BQP=2y°,
∵AB为⊙O的直径,
∴∠AOP+∠BOP=180°,
∴x+2y=180,
∴y=90﹣x,且0<x<180.
20.证明:∵AE是⊙O的直径,
∴∠ABE=90°,
∴∠E+∠BAE=90°,
∵AF⊥BC于D,
∴∠FAC+∠ACB=90°,
∵∠E=∠ACB,
∴∠BAE=∠FAC,
∴弧BE=弧CF,
∴BE=CF.
21.证明:∵点C是弧AE的中点,
∴∠B=∠CAE,
∵AB是⊙O的直径,
∴∠ACB=90°,
即∠ACF+∠BCD=90°,
∵CD⊥AB,
∴∠B+∠BCD=90°,
又∠ACF+∠BCD=90°,
∴∠B=∠ACF
∴∠B=∠CAF=∠ACF,
∴AF=CF.
22.解:在圆内接四边形ABCD中,∠BAC=180°﹣∠BDC=180°﹣150°=30°,
则弧BC的度数是60°,
又∵AB=AC,
∴弧AB=弧AC=150°,
∴弧ABC是210°,
∴∠APC=×210°=105°.
23.解:∵矩形、正方形的对角线相等且互相平分,
∴四个顶点到对角线交点距离相等,
∴矩形、正方形的四个顶点可在同一个圆上;
四个顶点在同一个圆上的四边形的对角互补.
24.解:(1)在优弧AB上取一点D,连接DA、DB,如图,
∵∠α=35°,
∴∠AOB=180°﹣∠OAB﹣∠OBA=180°﹣2×35°=110°,
∴∠D=∠AOB=55°,
∴∠ACB=180°﹣∠D=125°,
即β的度数为125°;
(2)∠ACB=90°+α.理由如下:
∵∠AOB=180°﹣2∠α,
∴∠D=∠AOB=(180°﹣2∠α)=90°﹣α,
∴∠ACB=180°﹣∠D=180°﹣(90°﹣α)=90°+α.
解:连OB,如图,
∵AB=OC,OB=OC,
∴AB=BO,
∴∠A=∠2,
而∠1=∠A+∠2,
∴∠1=2∠A,
∵OB=OE,
∴∠1=∠E,
∴∠E=2∠A,
而∠EOD=∠A+∠E=81°,
∴3∠A=81°,
所以∠A=27°.
同课章节目录
- 第1章 图形的相似
- 1.1 相似多边形
- 1.2 怎样判定三角形相似
- 1.3 相似三角形的性质
- 1.4 图形的位似
- 第2章 解直角三角形
- 2.1 锐角三角比
- 2.2 30°,45°,60°角的三角比
- 2.3 用计算器求锐角三角比
- 2.4 解直角三角形
- 2.5 解直角三角形的应用
- 第3章 对圆的进一步认识
- 3.1 圆的对称性
- 3.2 确定圆的条件
- 3.3 圆周角
- 3.4 直线与圆的位置关系
- 3.5 三角形的内切圆
- 3.6 弧长及扇形面积的计算
- 3.7 正多边形与圆
- 课题学习 图形变换与图案设计
- 第4章 一元二次方程
- 4.1 一元二次方程
- 4.2 用配方法解一元二次方程
- 4.3 用公式法解一元二次方程
- 4.4 用因式分解法解一元二次方程
- 4.5 一元二次方程的应用
- 4.6 一元二次方程根与系数的关系
