2.3等腰三角形 同步练习 2020-2021学年湘教版数学八年级上册(word版含答案)
文档属性
| 名称 | 2.3等腰三角形 同步练习 2020-2021学年湘教版数学八年级上册(word版含答案) |

|
|
| 格式 | docx | ||
| 文件大小 | 307.1KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 湘教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-10-21 00:00:00 | ||
图片预览


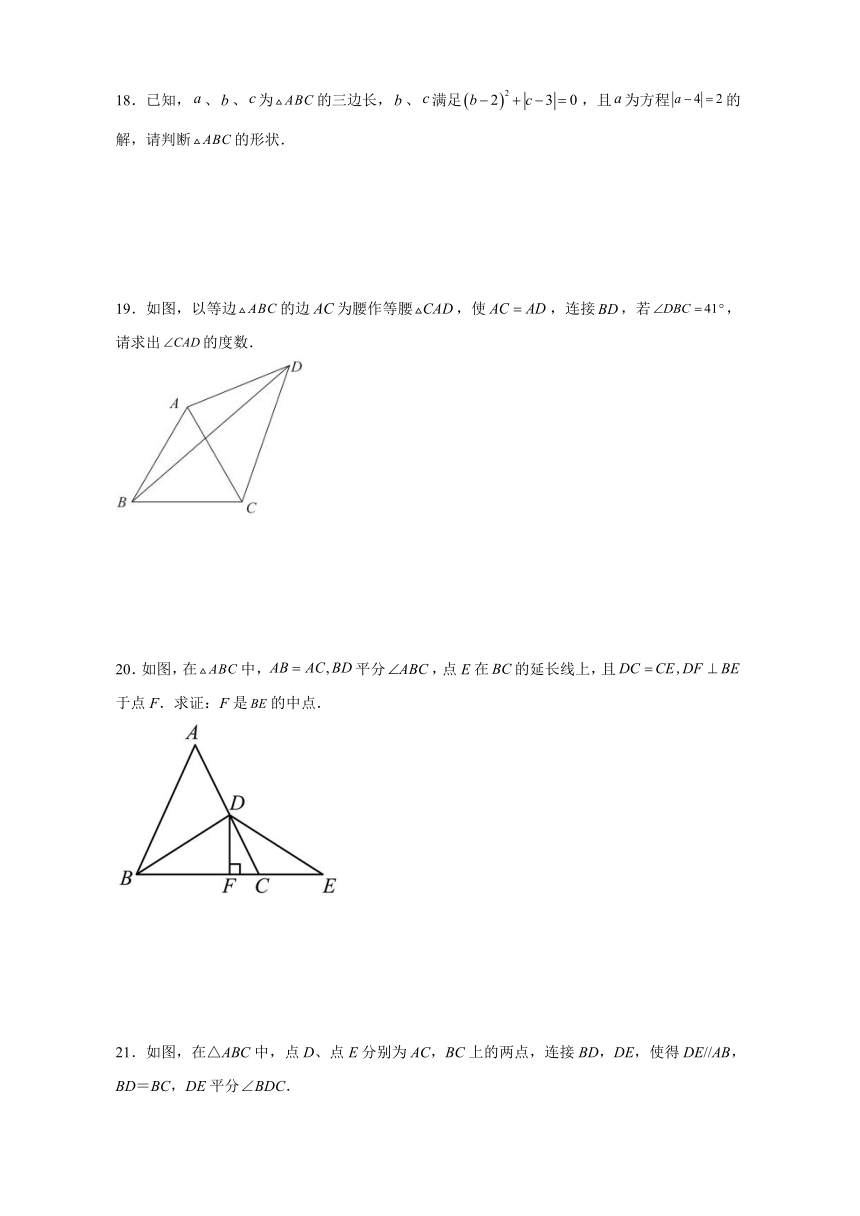

文档简介
等腰三角形
一、单选题
1.若一个等腰三角形的两边长分别为6和4,则该等腰三角形的周长是( )
A.13 B.14或16 C.16 D.14
2.在△ABC中,AB=AC,若∠B=72°,则∠A=( )
A.72° B.45° C.36° D.30°
3.如图,中,,D、E分别是两点,且,连接.则的度数为( )度·
A.45 B.52.5 C.67.5 D.75
4.如果的一个外角等于,且,则( )
A. B. C. D.或
5.如图,在中,,为边上的中线,,则的度数为( ).
A.55° B.65° C.75° D.85°
6.等腰三角形的一边长9cm,另一边长4cm,则它的周长是( )
A.22 cm B.17 cm C.22cm或17cm D.无法确定
7.如图,把绕着点顺时针方向旋转,得到△,点刚好落在边上.则
A. B. C. D.
8.如图,D是AB边上的中点,将ABC沿过D点的直线折叠,使点A落在BC上F处,若∠B=50°,则∠BDF的大小为( )
A.50° B.80° C.90° D.100°
9.下列三角形中,不是等腰三角形的是( )
A. B.
C. D.
10.如图,把等腰直角沿折叠,使点A落在边上的点E处.下面结论错误的是( ).
A. B. C. D.
11.中三边a、b、c满足,则这个三角形一定为( )
A.等边三角形 B.等腰三角形 C.等腰钝角三角形 D.等腰直角三角形
12.如图所示的正方形网格中,网格的交点称为格点,已知A,B是两格点,如果C也是图中的格点,且使得△ABC为等腰三角形,则符合条件的点C的个数是( )
A.7 B.8 C.9 D.10
二、填空题
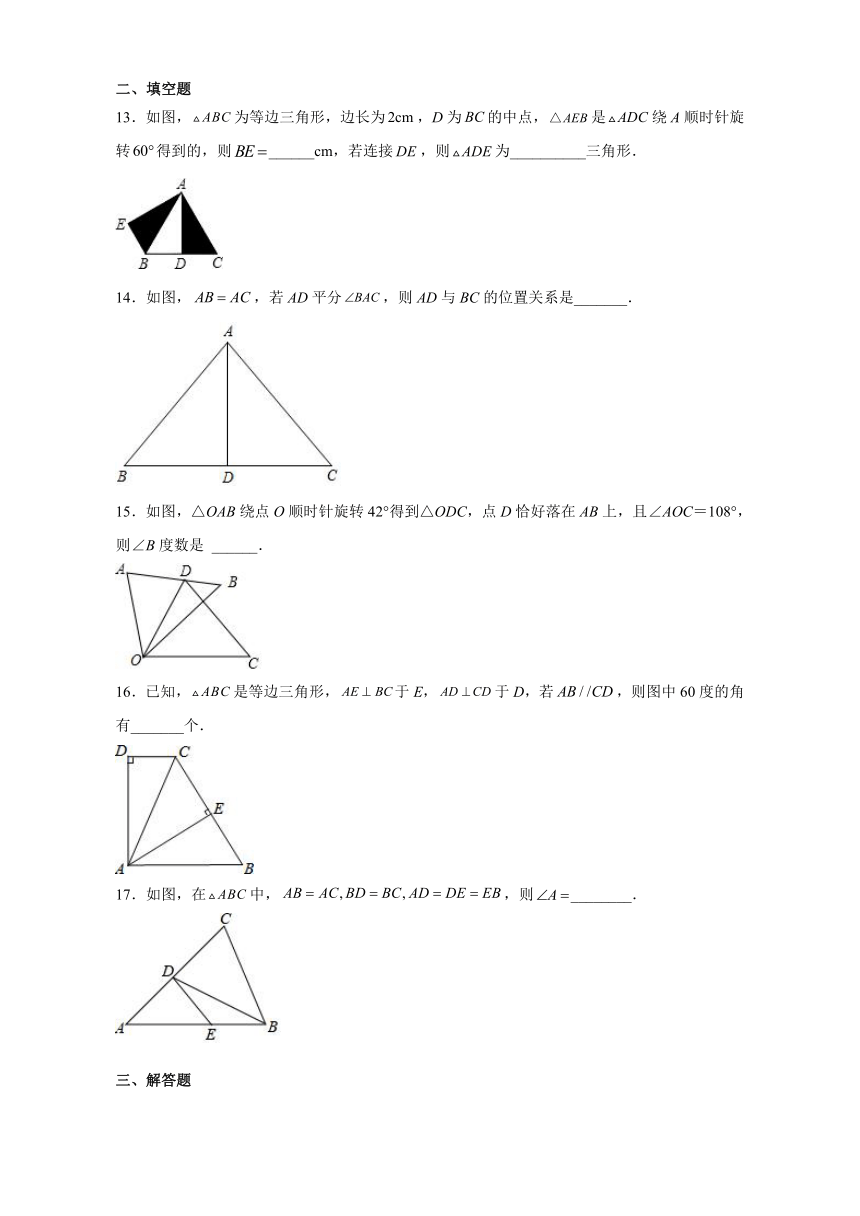
13.如图,为等边三角形,边长为,D为的中点,是绕A顺时针旋转得到的,则______cm,若连接,则为__________三角形.
14.如图,,若AD平分,则AD与BC的位置关系是_______.
15.如图,△OAB绕点O顺时针旋转42°得到△ODC,点D恰好落在AB上,且∠AOC=108°,则∠B度数是 ______.
16.已知,是等边三角形,于E,于D,若,则图中60度的角有_______个.
17.如图,在中,,则________.
三、解答题
18.已知,、、为的三边长,、满足,且为方程的解,请判断的形状.
19.如图,以等边的边为腰作等腰,使,连接,若,请求出的度数.
20.如图,在中,平分,点E在的延长线上,且于点F.求证:F是的中点.
21.如图,在△ABC中,点D、点E分别为AC,BC上的两点,连接BD,DE,使得DE//AB,BD=BC,DE平分∠BDC.
(1)求证:AD=BC;
(2)若∠BED=117°,求∠A的度数.
参考答案
1.B
解:等腰三角形的两边长分别为6和4
则另外一边为6或4
当另外一边为6时,三边分别为6,6,4,符合三角形三边条件,此时周长为16
当另外一边为4时,三边分别为6,4,4,符合三角形三边条件,此时周长为14
故选B
2.C
解:∵AB=AC,
∴∠C=∠B=72°,
∴∠A=180°﹣72°×2=36°.
故选:C.
3.C
解:∵AB=AC,
∴∠ABC=∠C,
∵∠ABC+∠C+∠A=180°,∠A=30°,
∴∠ABC=∠C=75°,
∵BD=BC=DE,
∴∠BED=∠BDE,∠BCD=∠BDC=75°,
∴∠DBC=180°-∠BCD-∠BDC=30°,
∴∠DBE=45°,
∴ ,
故选C.
4.D
解:分两种情况:(1)当这个150°的外角为顶角的外角时,则这个等腰三角形的顶角∠A为30°;
(2)当这个150°的外角为底角的外角时,可以得到这个等腰三角形的顶角∠A为180° 30° 30°=120°.
故选:D.
5.B
解:,为边上的中线,
,,
,
.
故选B.
6.A
解:①当腰为4cm时,三边为4cm,4cm,9cm,
∵4+4<9,
∴不符合三角形的三边关系定理,此种情况舍去;
②当腰为9cm时,三边为4cm,9cm,9cm,
此时符合三角形的三边关系定理,
此时等腰三角形的周长是4cm+9cm+9cm=22cm,
故选:A.
7.D
解:由题意可得:,
∵把绕着点顺时针方向旋转,得到△,点刚好落在边上,
∴,
∴.
故选:D.
8.B
解:∵折叠,
∴AD=DF,
∵D是AB边上的中点,
∴AD=BD,
∴BD=DF,
∵∠B=50°,
∴∠DFB=∠B=50°,
∴∠BDF=180°﹣∠B﹣∠DFB=80°.
故选:B.
9.A
解:A、由三角形内角和定理可得第三个角为:180゜-50゜-35゜=95゜,由等腰三角形的判定知,此三角形不是等腰三角形,故符合题意;
B、由三角形内角和定理可得第三个角为:180゜-90゜-45゜=45゜,由等腰三角形的判定知,此三角形是等腰三角形,故不符合题意;
C、由三角形内角和定理可得第三个角为:180゜-100゜-40゜=40゜,由等腰三角形的判定知,此三角形是等腰三角形,故不符合题意;
D、根据等腰三角形的定义知,此三角形是等腰三角形,故不符合题意;
故选:A.
10.B
解:根据折叠性质,有AB=BE,AD=DE,∠A=∠DEC=∠DEB=90°.
∴A正确;
又∠C=45°,
∴△CDE是等腰直角三角形,EC=DE,
∴AD=EC=DE,∴C正确;
∵∠DEC=90°,
∴CD>DE=EC.∴B错误;
∵AB=AC=AD+DC,
∴BC=BE+EC=AB+AD= AD+DC+AD=2AD+DC,故D正确.
故选:B.
11.B
解:∵ 则相乘的三项中至少有一项为0.
∴
∴
综上所述,三条边中至少有两条相等,所以△ABC一定为等腰三角形.
故选B.
12.B
解:如图所示:
∴符合条件的点C的个数为8.
故选B.
13.1 等边
解:∵为等边三角形,边长为,D为的中点,
∴,
∵是绕A顺时针旋转得到的,
∴,
∴为等边三角形,
故答案为:1;等边.
14.
解:∵,AD平分,
∴AD⊥BC,
∴AD与BC的位置关系是AD⊥BC.
故答案为AD⊥BC.
15.45°
解:由旋转性质可知,∠AOD=∠BOC=42°,
又∵∠AOC=108°,
∴∠BOD=108°-∠AOD-∠BOC=108°-42°-42°=24°,
∴∠AOB=∠AOD+∠BOD=42°+24°=66°,
∵AO=DO,
∵∠A=∠ADO=(180°-42°)÷2=69°,
∴∠B=180°-∠A-∠AOB=180°-69°-66°=45°,
故答案为:45°.
16.5
解:∵△ABC是等边三角形,AE⊥BC,
∴∠B=∠ACB=∠BAC=60°,∠CAE=∠BAE=30°,
∵AB∥CD,
∴∠ACD=∠CAB=60°,
∵AD⊥CD,
∴∠D=90°,
∴∠DAC=30°,
∴∠DAE=∠DAC+∠CAE=60°,
∴60度的角一共有5个,
故答案为:5.
17.
解:设∠A=x°
∵AB=AC,BD=BC
∴∠ABC=∠C=∠BDC
∵AD=DE=BE
∴∠A=∠AED=2∠EBD=2∠EDB
∴
∵∠ABC=∠C
∴
∴x=45
即∠A等于45°.
故答案为:
18.是等腰三角形.
解:∵,
∴,,
解得:,,
∵为方程的解,
∴,
解得:或2,
∵、、为的三边长,,
∴不合题意舍去,
∴,
∴是等腰三角形.
19..
解:∵△ABC是等边三角形
∴AB=AC,∠ABC=∠BAC=60°
∵AC=AD,∠DBC=41°
∴AB= AD,∠ABD=∠ABC-∠DBC=19°
∴∠ADB=∠ABD=19°
∴∠BAD=180°-∠ADB-∠ABD=142°
∴∠CAD=∠BAD-∠BAC=82°
20.见解析
解:∵,
∴,
∴,
∵,
∴,
∵,
∴,
∴,
∴,
∵,
∴是的中点.
21.(1)见解析;(2)39°.
解:(1)∵DE平分∠BDC,
∴∠BDE=∠CDE,
∵DE∥AB,
∴∠BDE=∠ABD,∠CDE=∠A,
∴∠ABD=∠A,
∴AD=BD,
又∵BD=BC,
∴AD=BC;
(2)∵∠BDC=∠A+∠ABD=2∠A,且BD=BC,
∴∠BDC=∠C=2∠A,
∴∠BED=∠C+∠CDE=2∠A+∠A=3∠A,
∵∠BED=117°,
∴∠A=39°.
一、单选题
1.若一个等腰三角形的两边长分别为6和4,则该等腰三角形的周长是( )
A.13 B.14或16 C.16 D.14
2.在△ABC中,AB=AC,若∠B=72°,则∠A=( )
A.72° B.45° C.36° D.30°
3.如图,中,,D、E分别是两点,且,连接.则的度数为( )度·
A.45 B.52.5 C.67.5 D.75
4.如果的一个外角等于,且,则( )
A. B. C. D.或
5.如图,在中,,为边上的中线,,则的度数为( ).
A.55° B.65° C.75° D.85°
6.等腰三角形的一边长9cm,另一边长4cm,则它的周长是( )
A.22 cm B.17 cm C.22cm或17cm D.无法确定
7.如图,把绕着点顺时针方向旋转,得到△,点刚好落在边上.则
A. B. C. D.
8.如图,D是AB边上的中点,将ABC沿过D点的直线折叠,使点A落在BC上F处,若∠B=50°,则∠BDF的大小为( )
A.50° B.80° C.90° D.100°
9.下列三角形中,不是等腰三角形的是( )
A. B.
C. D.
10.如图,把等腰直角沿折叠,使点A落在边上的点E处.下面结论错误的是( ).
A. B. C. D.
11.中三边a、b、c满足,则这个三角形一定为( )
A.等边三角形 B.等腰三角形 C.等腰钝角三角形 D.等腰直角三角形
12.如图所示的正方形网格中,网格的交点称为格点,已知A,B是两格点,如果C也是图中的格点,且使得△ABC为等腰三角形,则符合条件的点C的个数是( )
A.7 B.8 C.9 D.10
二、填空题
13.如图,为等边三角形,边长为,D为的中点,是绕A顺时针旋转得到的,则______cm,若连接,则为__________三角形.
14.如图,,若AD平分,则AD与BC的位置关系是_______.
15.如图,△OAB绕点O顺时针旋转42°得到△ODC,点D恰好落在AB上,且∠AOC=108°,则∠B度数是 ______.
16.已知,是等边三角形,于E,于D,若,则图中60度的角有_______个.
17.如图,在中,,则________.
三、解答题
18.已知,、、为的三边长,、满足,且为方程的解,请判断的形状.
19.如图,以等边的边为腰作等腰,使,连接,若,请求出的度数.
20.如图,在中,平分,点E在的延长线上,且于点F.求证:F是的中点.
21.如图,在△ABC中,点D、点E分别为AC,BC上的两点,连接BD,DE,使得DE//AB,BD=BC,DE平分∠BDC.
(1)求证:AD=BC;
(2)若∠BED=117°,求∠A的度数.
参考答案
1.B
解:等腰三角形的两边长分别为6和4
则另外一边为6或4
当另外一边为6时,三边分别为6,6,4,符合三角形三边条件,此时周长为16
当另外一边为4时,三边分别为6,4,4,符合三角形三边条件,此时周长为14
故选B
2.C
解:∵AB=AC,
∴∠C=∠B=72°,
∴∠A=180°﹣72°×2=36°.
故选:C.
3.C
解:∵AB=AC,
∴∠ABC=∠C,
∵∠ABC+∠C+∠A=180°,∠A=30°,
∴∠ABC=∠C=75°,
∵BD=BC=DE,
∴∠BED=∠BDE,∠BCD=∠BDC=75°,
∴∠DBC=180°-∠BCD-∠BDC=30°,
∴∠DBE=45°,
∴ ,
故选C.
4.D
解:分两种情况:(1)当这个150°的外角为顶角的外角时,则这个等腰三角形的顶角∠A为30°;
(2)当这个150°的外角为底角的外角时,可以得到这个等腰三角形的顶角∠A为180° 30° 30°=120°.
故选:D.
5.B
解:,为边上的中线,
,,
,
.
故选B.
6.A
解:①当腰为4cm时,三边为4cm,4cm,9cm,
∵4+4<9,
∴不符合三角形的三边关系定理,此种情况舍去;
②当腰为9cm时,三边为4cm,9cm,9cm,
此时符合三角形的三边关系定理,
此时等腰三角形的周长是4cm+9cm+9cm=22cm,
故选:A.
7.D
解:由题意可得:,
∵把绕着点顺时针方向旋转,得到△,点刚好落在边上,
∴,
∴.
故选:D.
8.B
解:∵折叠,
∴AD=DF,
∵D是AB边上的中点,
∴AD=BD,
∴BD=DF,
∵∠B=50°,
∴∠DFB=∠B=50°,
∴∠BDF=180°﹣∠B﹣∠DFB=80°.
故选:B.
9.A
解:A、由三角形内角和定理可得第三个角为:180゜-50゜-35゜=95゜,由等腰三角形的判定知,此三角形不是等腰三角形,故符合题意;
B、由三角形内角和定理可得第三个角为:180゜-90゜-45゜=45゜,由等腰三角形的判定知,此三角形是等腰三角形,故不符合题意;
C、由三角形内角和定理可得第三个角为:180゜-100゜-40゜=40゜,由等腰三角形的判定知,此三角形是等腰三角形,故不符合题意;
D、根据等腰三角形的定义知,此三角形是等腰三角形,故不符合题意;
故选:A.
10.B
解:根据折叠性质,有AB=BE,AD=DE,∠A=∠DEC=∠DEB=90°.
∴A正确;
又∠C=45°,
∴△CDE是等腰直角三角形,EC=DE,
∴AD=EC=DE,∴C正确;
∵∠DEC=90°,
∴CD>DE=EC.∴B错误;
∵AB=AC=AD+DC,
∴BC=BE+EC=AB+AD= AD+DC+AD=2AD+DC,故D正确.
故选:B.
11.B
解:∵ 则相乘的三项中至少有一项为0.
∴
∴
综上所述,三条边中至少有两条相等,所以△ABC一定为等腰三角形.
故选B.
12.B
解:如图所示:
∴符合条件的点C的个数为8.
故选B.
13.1 等边
解:∵为等边三角形,边长为,D为的中点,
∴,
∵是绕A顺时针旋转得到的,
∴,
∴为等边三角形,
故答案为:1;等边.
14.
解:∵,AD平分,
∴AD⊥BC,
∴AD与BC的位置关系是AD⊥BC.
故答案为AD⊥BC.
15.45°
解:由旋转性质可知,∠AOD=∠BOC=42°,
又∵∠AOC=108°,
∴∠BOD=108°-∠AOD-∠BOC=108°-42°-42°=24°,
∴∠AOB=∠AOD+∠BOD=42°+24°=66°,
∵AO=DO,
∵∠A=∠ADO=(180°-42°)÷2=69°,
∴∠B=180°-∠A-∠AOB=180°-69°-66°=45°,
故答案为:45°.
16.5
解:∵△ABC是等边三角形,AE⊥BC,
∴∠B=∠ACB=∠BAC=60°,∠CAE=∠BAE=30°,
∵AB∥CD,
∴∠ACD=∠CAB=60°,
∵AD⊥CD,
∴∠D=90°,
∴∠DAC=30°,
∴∠DAE=∠DAC+∠CAE=60°,
∴60度的角一共有5个,
故答案为:5.
17.
解:设∠A=x°
∵AB=AC,BD=BC
∴∠ABC=∠C=∠BDC
∵AD=DE=BE
∴∠A=∠AED=2∠EBD=2∠EDB
∴
∵∠ABC=∠C
∴
∴x=45
即∠A等于45°.
故答案为:
18.是等腰三角形.
解:∵,
∴,,
解得:,,
∵为方程的解,
∴,
解得:或2,
∵、、为的三边长,,
∴不合题意舍去,
∴,
∴是等腰三角形.
19..
解:∵△ABC是等边三角形
∴AB=AC,∠ABC=∠BAC=60°
∵AC=AD,∠DBC=41°
∴AB= AD,∠ABD=∠ABC-∠DBC=19°
∴∠ADB=∠ABD=19°
∴∠BAD=180°-∠ADB-∠ABD=142°
∴∠CAD=∠BAD-∠BAC=82°
20.见解析
解:∵,
∴,
∴,
∵,
∴,
∵,
∴,
∴,
∴,
∵,
∴是的中点.
21.(1)见解析;(2)39°.
解:(1)∵DE平分∠BDC,
∴∠BDE=∠CDE,
∵DE∥AB,
∴∠BDE=∠ABD,∠CDE=∠A,
∴∠ABD=∠A,
∴AD=BD,
又∵BD=BC,
∴AD=BC;
(2)∵∠BDC=∠A+∠ABD=2∠A,且BD=BC,
∴∠BDC=∠C=2∠A,
∴∠BED=∠C+∠CDE=2∠A+∠A=3∠A,
∵∠BED=117°,
∴∠A=39°.
同课章节目录
