3.2平行线分线段成比例 同步达标测评 2021-2022学年湘教版九年级数学上册(word版含答案)
文档属性
| 名称 | 3.2平行线分线段成比例 同步达标测评 2021-2022学年湘教版九年级数学上册(word版含答案) | 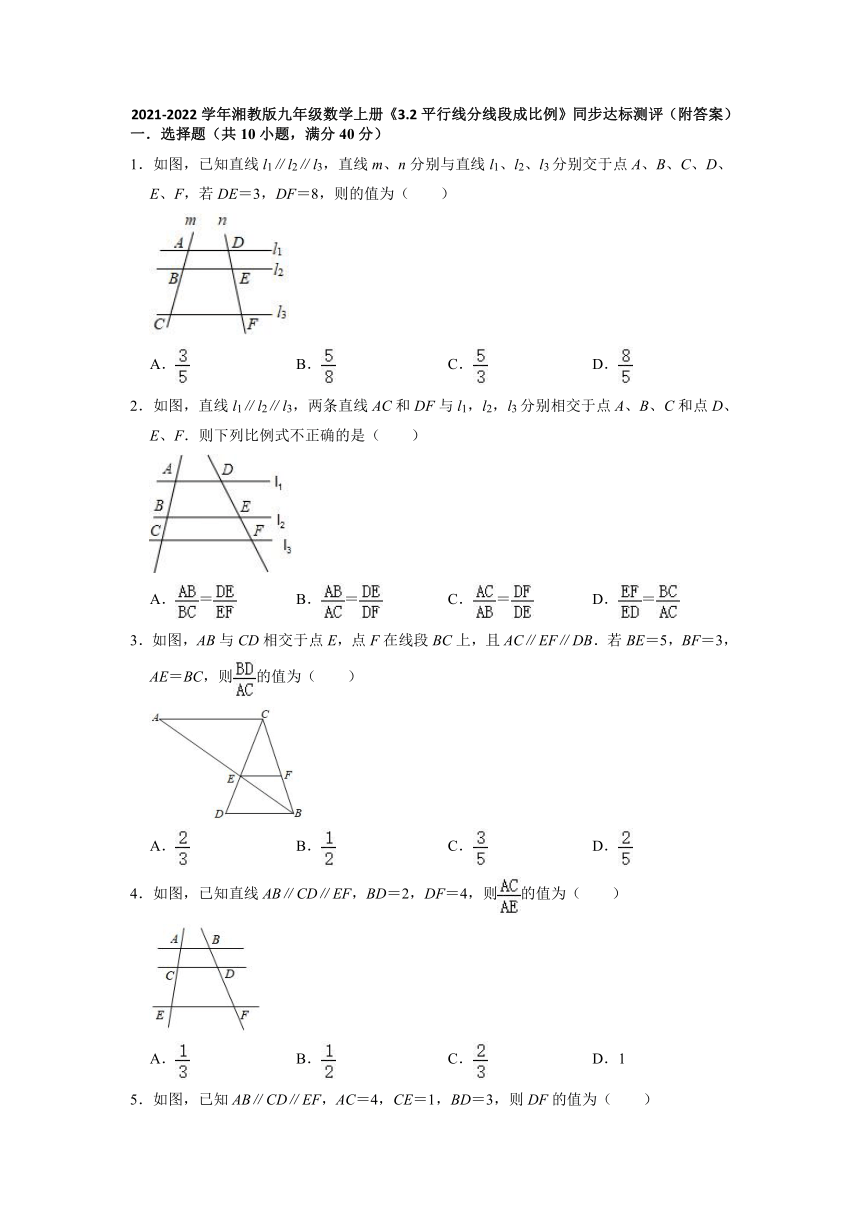 | |
| 格式 | doc | ||
| 文件大小 | 394.8KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 湘教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-10-21 08:08:22 | ||
图片预览





文档简介
2021-2022学年湘教版九年级数学上册《3.2平行线分线段成比例》同步达标测评(附答案)
一.选择题(共10小题,满分40分)
1.如图,已知直线l1∥l2∥l3,直线m、n分别与直线l1、l2、l3分别交于点A、B、C、D、E、F,若DE=3,DF=8,则的值为( )
A. B. C. D.
2.如图,直线l1∥l2∥l3,两条直线AC和DF与l1,l2,l3分别相交于点A、B、C和点D、E、F.则下列比例式不正确的是( )
A.= B.= C.= D.=
3.如图,AB与CD相交于点E,点F在线段BC上,且AC∥EF∥DB.若BE=5,BF=3,AE=BC,则的值为( )
A. B. C. D.
4.如图,已知直线AB∥CD∥EF,BD=2,DF=4,则的值为( )
A. B. C. D.1
5.如图,已知AB∥CD∥EF,AC=4,CE=1,BD=3,则DF的值为( )
A. B. C. D.1
6.在△ABC中,点D、E分别在边AB、AC上,AD=2,AB=6,那么下列各条件中,不—定能判定DE∥BC的是( )
A. B. C. D.
7.如图,在△ABC中,D是BC上一点,连接AD,,F是AD的中点,连接BF并延长交AC于E,则的值是( )
A. B. C. D.
8.如图,△ABC中,AB=AC=12,BC=8,点D在BC边上,且BD<BC,△ABD与△AED关于AD对称,AE与BC交于点F,则的最小值为( )
A. B. C. D.
9.如图.AB∥CD∥EF,AF、BE交于点G,下列比例式错误的是( )
A. B. C. D.
10.如图,AG:GD=3:1,BD:DC=2:3,则AE:EC的值是( )
A.8:7 B.8:5 C.3:2 D.6:5
二.填空题(共6小题,满分24分)
11.如图,a∥b∥c,直线m、n与a、b、c分别相交于点A、B、C和点D、B、F.若AB=3,BC=5,DE=4,则EF的长为 .
12.如图,在△ABC中,AB=5,AC=4,若进行以下操作,在边BC上从左到右依次取点D1、D2、D3、D4、…;过点D1作AB、AC的平行线分别交AC、AB于点E1、F1;过点D2作AB、AC的平行线分别交AC、AB于点E2、F2;过点D3作AB、AC的平行线分别交AC、AB于点E3、F3…,则4(D1E1+D2E2+…+D2021E2021)+5(D1F1+D2F2+…+D2021F2021)= .
13.如图,AD∥BE∥CF,AB=3,BC=6,DE=2,则EF的值为 .
14.如图,已知l1∥l2∥l3,直线l4、l5被这组平行线所截,且直线l4、l5相交于点E,已知AE=EF=1,FB=3,则= .
15.如图,在△ABC中,DE∥BC,DE与边AB相交于点D,与边AC相交于点E,如果AD=3,BD=4,AE=2,那么AC= .
16.如图是一架梯子的示意图,其中AA1∥BB1∥CC1∥DD1,且AB=BC=CD.为使其更稳固,在A,D1间加绑一条安全绳(线段AD1)量得AE=0.4m,则AD1= m.
三.解答题(共9小题,满分56分)
17.阅读与计算,请阅读以下材料,并完成相应的问题.
角平分线分线段成比例定理,如图1,在△ABC中,AD平分∠BAC,则=.下面是这个定理的部分证明过程.
证明:如图2,过C作CE∥DA.交BA的延长线于E.…
任务:(1)请按照上面的证明思路,写出该证明的剩余部分;
(2)填空:如图3,已知Rt△ABC中,AB=3,BC=4,∠ABC=90°,AD平分∠BAC,则△ABD的周长是 .
18.如图,已知AD∥BE∥CF,它们依次交直线l1、l2于点A、B、C和点D、E、F,且AB=6,BC=8.
(1)求的值;
(2)当AD=5,CF=19时,求BE的长.
19.如图,在△ABC中,AB=10,AC=8,点D在边AB上,DE∥BC交AC于点E,如果BD=4,求AE的长.
20.已知:如图,在△ABC中,DE∥BC,EF∥AB,试判断成立吗?并说明理由.
21.如图,在△ABC中,点D,E分别在AB,AC的边上,DE∥BC,AD=6,DB=3,AE=4,求AC的长.
22.如图所示,l1∥l2∥l3,且AB=2BC,DF=5cm,AG=4cm.求GF,AF,EF的长.
23.如图:AD∥EG∥BC,EG分别交AB,DB,AC于点E,F,G,已知AD=5,BC=10,AE=9,AB=12.求EG,FG的长.
24.如图,a∥b∥c,直线m,n与直线a,b,c分别相交于点A,B,C和点D,E,F.若AB=3,BC=5,DE=4,求EF的长.
25.如图,BD∥直线m,求证:PM PN=PR PS.
参考答案
一.选择题(共10小题,满分40分)
1.解:∵l1∥l2∥l3,
∴,
∵DE=3,DF=8,
∴,
即=,
故选:B.
2.解:∵l1∥l2∥l3,
∴,,,,
故选:D.
3.解:设CF=x,
∵EF∥AC,
∴=,
∴=,
解得x=,
∴CF=,
∵EF∥DB,
∴===.
故选:A.
4.解:∵AB∥CD∥EF,BD=2,DF=4,
∴===,
故选:A.
5.解:∵AB∥CD∥EF,
∴=,即=,
解得,DF=,
故选:C.
6.解:
∵AD=2,AB=6,
∴AD:AB=1:3,
∵AE:AC=1:3,
∴AE:AC=AD:AB,
∴DE∥BC,故结论B不符合题意;
∵AE:EC=1:2,
∴AE:AC=1:(1+2)=1:3,
∴AE:AC=AD:AB,
∴DE∥BC,故结论C不符合题意;
∵EC:AC=2:3,
∴AE:AC=(3﹣2):3=1:3,
∴AE:AC=AD:AB,
∴DE∥BC,故结论C不符合题意;
由DE:BC=1:3,得不出DE∥BC,故结论A符合题意;
故选:A.
7.解:过D点作DH∥BE交AC于H,如图,
∵F点为AD的中点,
∴AF=FD,
∵FE∥DH,
∴==1,即AE=EH,
∵DH∥BE,
∴==,CH=3EH,
∴=.
故选:A.
8.解:作AG⊥BC于G,作DH⊥AE于H,
∵AB=AC=12,BC=8,AG⊥BC,
∴BG=CG=BC=4,
∴AG===8,
∵△ABD与△AED关于AD对称,
∴∠B=∠E,BD=ED,
∵∠AGB=∠DHE=90°,
∴,即,
∴,
∵BD=ED,
∵DF≥DH,
∴,
当AE⊥BC时,F与H重合,即DF⊥AE,此时DF=DH,
∴的最小值为,
故选:C.
9.解:A、由AB∥CD∥EF,则,所以A选项的结论正确;
B、由AB∥CD∥EF,则,所以B选项的结论正确;
C、由AB∥CD∥EF,则,所以C选项的结论正确;
D、由AB∥CD∥EF,则,所以D选项的结论错误;
故选:D.
10.解:过点D作DF∥BE交AC于点F,
则==,==3,
∴AE:EC=6:5,
故选:D.
二.填空题(共6小题,满分24分)
11.解:∵a∥b∥c,AB=3,BC=5,DE=4,
∴=,即=,
解得,EF=,
故答案为:.
12.解:∵D1F1∥AC,
∴.
∵D1F1∥AC,D1E1∥AB,
∴四边形D1E1AF1为平行四边形.
∴D1E1=AF1.
∴BF1=AB﹣AF1=AB﹣D1E1.
∴.
将AB=5,AC=4代入上式得:4D1E1+5D1F1=20.
同理可得:4D2E2+5D2F2=20,
…
4D2021E2021+5D2021F2021=20,
∴4(D1E1+D2E2+…+D2021E2021)+5(D1F1+D2F2+…+D2021F2021)
=4D1E1+5D1F1+4D2E2+5D2F2+…+4D2021E2021+5D2021F2021
=20+20+…+20
=2021×20
=40420.
故答案为40420.
13.解:∵AD∥BE∥CF,
∴=,
∵AB=3,BC=6,DE=2,
∴EF===4,
故答案为:4.
14.解:∵l1∥l2,AE=EF=1,
∴==1,
∴FG=AC;
∵l2∥l3,
∴==,
∴==,
故答案为.
15.解:∵DE∥BC,
∴=,
∵AD=3,BD=4,AE=2,
∴=,
解得EC=,
∴AC=AE+EC=2+=,
故答案为:.
16.解:∵BB1∥CC1,
∴=,
∵AB=BC,
∴AE=EF,
同理可得:AE=EF=FD1,
∵AE=0.4m,
∴AD1=0.4×3=1.2(m),
故答案为:1.2.
三.解答题(共9小题,满分56分)
17.(1)证明:如图2,过C作CE∥DA.交BA的延长线于E,
∵CE∥AD,
∴=,∠2=∠ACE,∠1=∠E,
∵∠1=∠2,
∴∠ACE=∠E,
∴AE=AC,
∴=;
(2)解:如图3,∵AB=3,BC=4,∠ABC=90°,
∴AC=5,
∵AD平分∠BAC,
∴=,即=,
∴BD=BC=,
∴AD===,
∴△ABD的周长=+3+=.
故答案为.
18.解:(1)∵AD∥BE∥CF,
∴===;
(2)过D点作DM∥AC交CF于M,交BE于N,如图,
∵AD∥BN∥CM,AC∥DM,
∴四边形ABND和四边形ACMD都是平行四边形,
∴BN=AD=5,CM=AD=5,
∴MF=CF﹣CM=19﹣5=14,
∵NE∥MF,
∴==,
∴NE=MF=×14=6,
∴BE=BN+NE=5+6=11.
19.解:∵AB=10,BD=4,
∴AD=AB﹣BD=6,
∵DE∥BC,
∴=,
∴=,
解得:AE=4.8.
20.解:成立.
理由如下:
∵DE∥BC,
∴.
∵EF∥AB,
∴.
∴.
21.解:∵DE∥BC,
∴.
∵AD=6,DB=3,AE=4,
∴.
∴EC=2.
∴AC=AE+EC=6.
22.解:∵l2∥l3,
∴=,
而AG=4,AB=2BC,
∴=2,
∴GF=2(cm);
∴AF=AG+GF=4cm+2cm=6cm;
∵l1∥l2∥l3,
∴=,即=,
∴EF=(cm).
答:GF,AF,EF的长分别为2cm,6cm,cm.
23.解:∵△ABC中,EG∥BC,
∴,
∵BC=10,AE=9,AB=12,
∴=,
∴EG=,
∵△BAD中,EF∥AD,
∴=,
∵AD=5,AE=9,AB=12,
∴=,
∴EF=.
∴FG=EG﹣EF=﹣=.
24.解:∵a∥b∥c,
∴,
即,
解得:EF=.
25.证明:
∵BD∥直线m,
∴=,=,
∴=,
∴=,
∵BD∥直线m,
∴=,=,
∴=,
∴=,
∴=,
∴PM PN=PR PS.
一.选择题(共10小题,满分40分)
1.如图,已知直线l1∥l2∥l3,直线m、n分别与直线l1、l2、l3分别交于点A、B、C、D、E、F,若DE=3,DF=8,则的值为( )
A. B. C. D.
2.如图,直线l1∥l2∥l3,两条直线AC和DF与l1,l2,l3分别相交于点A、B、C和点D、E、F.则下列比例式不正确的是( )
A.= B.= C.= D.=
3.如图,AB与CD相交于点E,点F在线段BC上,且AC∥EF∥DB.若BE=5,BF=3,AE=BC,则的值为( )
A. B. C. D.
4.如图,已知直线AB∥CD∥EF,BD=2,DF=4,则的值为( )
A. B. C. D.1
5.如图,已知AB∥CD∥EF,AC=4,CE=1,BD=3,则DF的值为( )
A. B. C. D.1
6.在△ABC中,点D、E分别在边AB、AC上,AD=2,AB=6,那么下列各条件中,不—定能判定DE∥BC的是( )
A. B. C. D.
7.如图,在△ABC中,D是BC上一点,连接AD,,F是AD的中点,连接BF并延长交AC于E,则的值是( )
A. B. C. D.
8.如图,△ABC中,AB=AC=12,BC=8,点D在BC边上,且BD<BC,△ABD与△AED关于AD对称,AE与BC交于点F,则的最小值为( )
A. B. C. D.
9.如图.AB∥CD∥EF,AF、BE交于点G,下列比例式错误的是( )
A. B. C. D.
10.如图,AG:GD=3:1,BD:DC=2:3,则AE:EC的值是( )
A.8:7 B.8:5 C.3:2 D.6:5
二.填空题(共6小题,满分24分)
11.如图,a∥b∥c,直线m、n与a、b、c分别相交于点A、B、C和点D、B、F.若AB=3,BC=5,DE=4,则EF的长为 .
12.如图,在△ABC中,AB=5,AC=4,若进行以下操作,在边BC上从左到右依次取点D1、D2、D3、D4、…;过点D1作AB、AC的平行线分别交AC、AB于点E1、F1;过点D2作AB、AC的平行线分别交AC、AB于点E2、F2;过点D3作AB、AC的平行线分别交AC、AB于点E3、F3…,则4(D1E1+D2E2+…+D2021E2021)+5(D1F1+D2F2+…+D2021F2021)= .
13.如图,AD∥BE∥CF,AB=3,BC=6,DE=2,则EF的值为 .
14.如图,已知l1∥l2∥l3,直线l4、l5被这组平行线所截,且直线l4、l5相交于点E,已知AE=EF=1,FB=3,则= .
15.如图,在△ABC中,DE∥BC,DE与边AB相交于点D,与边AC相交于点E,如果AD=3,BD=4,AE=2,那么AC= .
16.如图是一架梯子的示意图,其中AA1∥BB1∥CC1∥DD1,且AB=BC=CD.为使其更稳固,在A,D1间加绑一条安全绳(线段AD1)量得AE=0.4m,则AD1= m.
三.解答题(共9小题,满分56分)
17.阅读与计算,请阅读以下材料,并完成相应的问题.
角平分线分线段成比例定理,如图1,在△ABC中,AD平分∠BAC,则=.下面是这个定理的部分证明过程.
证明:如图2,过C作CE∥DA.交BA的延长线于E.…
任务:(1)请按照上面的证明思路,写出该证明的剩余部分;
(2)填空:如图3,已知Rt△ABC中,AB=3,BC=4,∠ABC=90°,AD平分∠BAC,则△ABD的周长是 .
18.如图,已知AD∥BE∥CF,它们依次交直线l1、l2于点A、B、C和点D、E、F,且AB=6,BC=8.
(1)求的值;
(2)当AD=5,CF=19时,求BE的长.
19.如图,在△ABC中,AB=10,AC=8,点D在边AB上,DE∥BC交AC于点E,如果BD=4,求AE的长.
20.已知:如图,在△ABC中,DE∥BC,EF∥AB,试判断成立吗?并说明理由.
21.如图,在△ABC中,点D,E分别在AB,AC的边上,DE∥BC,AD=6,DB=3,AE=4,求AC的长.
22.如图所示,l1∥l2∥l3,且AB=2BC,DF=5cm,AG=4cm.求GF,AF,EF的长.
23.如图:AD∥EG∥BC,EG分别交AB,DB,AC于点E,F,G,已知AD=5,BC=10,AE=9,AB=12.求EG,FG的长.
24.如图,a∥b∥c,直线m,n与直线a,b,c分别相交于点A,B,C和点D,E,F.若AB=3,BC=5,DE=4,求EF的长.
25.如图,BD∥直线m,求证:PM PN=PR PS.
参考答案
一.选择题(共10小题,满分40分)
1.解:∵l1∥l2∥l3,
∴,
∵DE=3,DF=8,
∴,
即=,
故选:B.
2.解:∵l1∥l2∥l3,
∴,,,,
故选:D.
3.解:设CF=x,
∵EF∥AC,
∴=,
∴=,
解得x=,
∴CF=,
∵EF∥DB,
∴===.
故选:A.
4.解:∵AB∥CD∥EF,BD=2,DF=4,
∴===,
故选:A.
5.解:∵AB∥CD∥EF,
∴=,即=,
解得,DF=,
故选:C.
6.解:
∵AD=2,AB=6,
∴AD:AB=1:3,
∵AE:AC=1:3,
∴AE:AC=AD:AB,
∴DE∥BC,故结论B不符合题意;
∵AE:EC=1:2,
∴AE:AC=1:(1+2)=1:3,
∴AE:AC=AD:AB,
∴DE∥BC,故结论C不符合题意;
∵EC:AC=2:3,
∴AE:AC=(3﹣2):3=1:3,
∴AE:AC=AD:AB,
∴DE∥BC,故结论C不符合题意;
由DE:BC=1:3,得不出DE∥BC,故结论A符合题意;
故选:A.
7.解:过D点作DH∥BE交AC于H,如图,
∵F点为AD的中点,
∴AF=FD,
∵FE∥DH,
∴==1,即AE=EH,
∵DH∥BE,
∴==,CH=3EH,
∴=.
故选:A.
8.解:作AG⊥BC于G,作DH⊥AE于H,
∵AB=AC=12,BC=8,AG⊥BC,
∴BG=CG=BC=4,
∴AG===8,
∵△ABD与△AED关于AD对称,
∴∠B=∠E,BD=ED,
∵∠AGB=∠DHE=90°,
∴,即,
∴,
∵BD=ED,
∵DF≥DH,
∴,
当AE⊥BC时,F与H重合,即DF⊥AE,此时DF=DH,
∴的最小值为,
故选:C.
9.解:A、由AB∥CD∥EF,则,所以A选项的结论正确;
B、由AB∥CD∥EF,则,所以B选项的结论正确;
C、由AB∥CD∥EF,则,所以C选项的结论正确;
D、由AB∥CD∥EF,则,所以D选项的结论错误;
故选:D.
10.解:过点D作DF∥BE交AC于点F,
则==,==3,
∴AE:EC=6:5,
故选:D.
二.填空题(共6小题,满分24分)
11.解:∵a∥b∥c,AB=3,BC=5,DE=4,
∴=,即=,
解得,EF=,
故答案为:.
12.解:∵D1F1∥AC,
∴.
∵D1F1∥AC,D1E1∥AB,
∴四边形D1E1AF1为平行四边形.
∴D1E1=AF1.
∴BF1=AB﹣AF1=AB﹣D1E1.
∴.
将AB=5,AC=4代入上式得:4D1E1+5D1F1=20.
同理可得:4D2E2+5D2F2=20,
…
4D2021E2021+5D2021F2021=20,
∴4(D1E1+D2E2+…+D2021E2021)+5(D1F1+D2F2+…+D2021F2021)
=4D1E1+5D1F1+4D2E2+5D2F2+…+4D2021E2021+5D2021F2021
=20+20+…+20
=2021×20
=40420.
故答案为40420.
13.解:∵AD∥BE∥CF,
∴=,
∵AB=3,BC=6,DE=2,
∴EF===4,
故答案为:4.
14.解:∵l1∥l2,AE=EF=1,
∴==1,
∴FG=AC;
∵l2∥l3,
∴==,
∴==,
故答案为.
15.解:∵DE∥BC,
∴=,
∵AD=3,BD=4,AE=2,
∴=,
解得EC=,
∴AC=AE+EC=2+=,
故答案为:.
16.解:∵BB1∥CC1,
∴=,
∵AB=BC,
∴AE=EF,
同理可得:AE=EF=FD1,
∵AE=0.4m,
∴AD1=0.4×3=1.2(m),
故答案为:1.2.
三.解答题(共9小题,满分56分)
17.(1)证明:如图2,过C作CE∥DA.交BA的延长线于E,
∵CE∥AD,
∴=,∠2=∠ACE,∠1=∠E,
∵∠1=∠2,
∴∠ACE=∠E,
∴AE=AC,
∴=;
(2)解:如图3,∵AB=3,BC=4,∠ABC=90°,
∴AC=5,
∵AD平分∠BAC,
∴=,即=,
∴BD=BC=,
∴AD===,
∴△ABD的周长=+3+=.
故答案为.
18.解:(1)∵AD∥BE∥CF,
∴===;
(2)过D点作DM∥AC交CF于M,交BE于N,如图,
∵AD∥BN∥CM,AC∥DM,
∴四边形ABND和四边形ACMD都是平行四边形,
∴BN=AD=5,CM=AD=5,
∴MF=CF﹣CM=19﹣5=14,
∵NE∥MF,
∴==,
∴NE=MF=×14=6,
∴BE=BN+NE=5+6=11.
19.解:∵AB=10,BD=4,
∴AD=AB﹣BD=6,
∵DE∥BC,
∴=,
∴=,
解得:AE=4.8.
20.解:成立.
理由如下:
∵DE∥BC,
∴.
∵EF∥AB,
∴.
∴.
21.解:∵DE∥BC,
∴.
∵AD=6,DB=3,AE=4,
∴.
∴EC=2.
∴AC=AE+EC=6.
22.解:∵l2∥l3,
∴=,
而AG=4,AB=2BC,
∴=2,
∴GF=2(cm);
∴AF=AG+GF=4cm+2cm=6cm;
∵l1∥l2∥l3,
∴=,即=,
∴EF=(cm).
答:GF,AF,EF的长分别为2cm,6cm,cm.
23.解:∵△ABC中,EG∥BC,
∴,
∵BC=10,AE=9,AB=12,
∴=,
∴EG=,
∵△BAD中,EF∥AD,
∴=,
∵AD=5,AE=9,AB=12,
∴=,
∴EF=.
∴FG=EG﹣EF=﹣=.
24.解:∵a∥b∥c,
∴,
即,
解得:EF=.
25.证明:
∵BD∥直线m,
∴=,=,
∴=,
∴=,
∵BD∥直线m,
∴=,=,
∴=,
∴=,
∴=,
∴PM PN=PR PS.
同课章节目录
- 第1章 反比例函数
- 1.1 反比例函数
- 1.2 反比例函数的图像与性质
- 1.3 反比例函数的应用
- 第2章 一元二次方程
- 2.1 一元二次方程
- 2.2 一元二次方程的解法
- 2.3 一元二次方程根的判别式
- 2.4 一元二次方程根与系数的关系
- 2.5 一元二次方程的应用
- 第3章 图形的相似
- 3.1 比例线段
- 3.2 平行线分线段成比例
- 3.3 相似图形
- 3.4 相似三角形的判定与性质
- 3.5 相似三角形的应用
- 3.6 位似
- 第4章 锐角三角函数
- 4.1 正弦和余弦
- 4.2 正切
- 4.3 解直角三角形
- 4.4 解直接三角形的应用
- 第5章 用样本推断总体
- 5.1 总体平均数与方差的估计
- 5.2 统计的简单应用
