黑龙江省牡丹江市林口县2020-2021学年七年级下学期期末考试数学试题(word版含答案)
文档属性
| 名称 | 黑龙江省牡丹江市林口县2020-2021学年七年级下学期期末考试数学试题(word版含答案) |

|
|
| 格式 | zip | ||
| 文件大小 | 1.2MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版(五四学制) | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-10-20 00:00:00 | ||
图片预览




文档简介
2020—2021学年度第二学期期末质量测查
七年级数学试题
题号 一 二 三 总分 核分人
21 22 23 24 25 26
得分
得分 评卷人
一、选择题(每小题3分,满分36分)
1.如图所示,由图案(1)平移得到的图案是( )
图(1) A B C D
2.在实数 ,, ,,,0中,无理数的个数为( )
A.1个 B.2个 C.3个 D.4个
3.不等式6-3x>0的解集在数轴上表示为( )
A. B.
C. D.
4.如图,10块相同的长方形墙砖拼成一个大长方形,设长方形墙砖的长和宽分别为x厘米和y厘米,则依题意所列方程组正确的是( )
A. B.
C. D.
5.如图,已知,,
平分,则( ).
A.32° B.60° C.58° D.64°
6.若是关于x、y的二元一次方程ax-5y=1的解,则a的值为( )
A. -5 B. -1 C. 9 D. 11
7.下列四个命题是真命题的是( )
A.两条直线被第三条直线所截,同位角相等
B. 互补的两个角一定是邻补角
C. 在同一平面内,垂直于同一条直线的两条直线互相平行
D. 相等的角是对顶角
8.在一个样本中,40个数据分别落在5个小组内,第1,2,3,5小组的频数分别是6,5,15,7,则第4小组的频数是( )
A. 7 B. 8 C. 9 D. 10
9.下列四个命题:①若a>b,则a-3>b-3;②若a>b,则a+c>b+c;③若a>b,则-3a<-3b;④若a>b,则ac>bc.其中,真命题有( )
A. ①③④ B②③④ C..①②③④ D.①②③
10.如图,直线AB,CD相交于点O,OA平分∠EOC,若∠EOC︰∠EOD=2︰3,则∠BOD的度数为( )
A.36° B.40° C.35° D.45°
(第10题) (第12题)
11.若方程组的解满足x+y>0,则m的取值范围是( )
A. m>-3 B. m>-2 C. m>-1 D. m>0
12.如图,现给出下列条件:①,②,③,④,⑤.其中能够得到AB//CD的条件的个数( )
A2个 B.3个 C.4个 D.5个
得分 评卷人
2、填空题(每小题3分,满分24分)
13.-8的立方根是_____,36的平方根是_____.
14.下列调查中,调查方式选择正确的是_____
①为了了解一批灯泡的使用寿命,选择抽样调查.②为了了解某公园全年的游客流量,选择抽样调查。③为了了解某1000枚炮弹的杀伤半径,选择全面调查。④为了了解一批袋装食品是否有防腐剂,选择全面调查。
15.在两个连续整数a和b之间,a<<b,那么b-a的值为_____.
16.点P(a,b)距离x轴2个单位长度,距离y轴3个单位长度且ab>0,则P点的坐标是 .
17.点为线段上一点,不与点、重合,于点,若,则的度数为 .
18.若方程是关于,的二元一次方程,则 .
19.若关于x的不等式2x-a≤4有3个非负整数解,则a的取值范围是 .
20.在平面直角坐标系中,对于点P(x,y),我们把点P′(-y+1,x+1)叫做点P的幸运点.已知点A1的幸运点为A2,点A2的幸运点为A3,点A3的幸运点为A4,……,这样依次得到点A1,A2,A3,…,An.若点A1的坐标为(3,1),则点A2020的坐标为 .
得分 评卷人
三、解答题(满分60分)
21.(第(1)题4分,第(2)(3)小题每题6分,满分16分)
(1)计算:.
(2)解方程组:
(3)解不等式组,并写出它的正整数解.
22.(本小题满分6分)
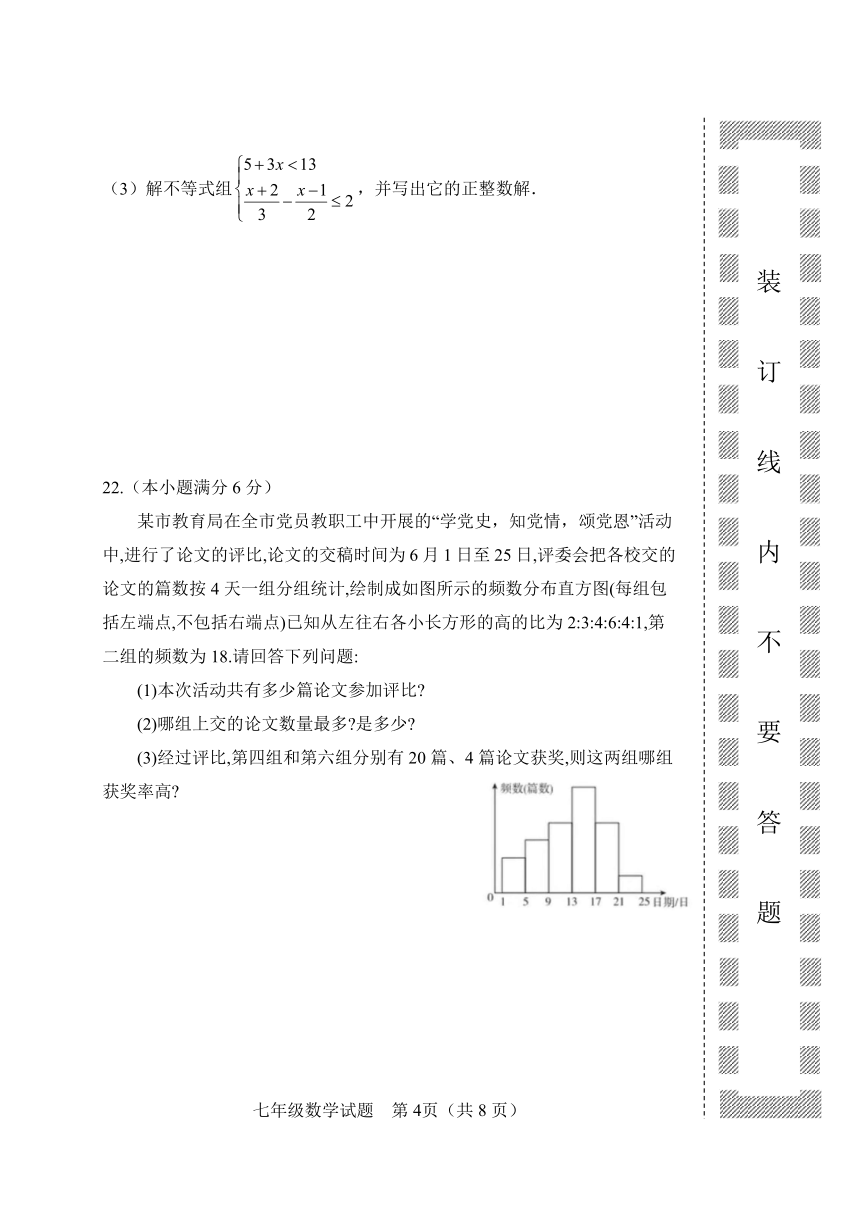
某市教育局在全市党员教职工中开展的“学党史,知党情,颂党恩”活动中,进行了论文的评比,论文的交稿时间为6月1日至25日,评委会把各校交的论文的篇数按4天一组分组统计,绘制成如图所示的频数分布直方图(每组包括左端点,不包括右端点)已知从左往右各小长方形的高的比为2:3:4:6:4:1,第二组的频数为18.请回答下列问题:
(1)本次活动共有多少篇论文参加评比
(2)哪组上交的论文数量最多 是多少
(3)经过评比,第四组和第六组分别有20篇、4篇论文获奖,则这两组哪组获奖率高
23.(本小题满分8分)
如图,三角形ABC在平面直角坐标系中第二象限内,顶点A的坐标是,先把三角形ABC向右平移4个单位,再向下平移3个单位得到三角形.
(1)请在图中作出三角形;
(2)点的坐标为_____;点的坐标为______;点的坐标为_____;
(3)求三角形的面积.
24.(本小题满分10分)
如图,已知.
(1)求证:
证明:∵EF//DB(已知)
(_____________________).
又∵∠1=∠2(已知),
___________(等量代换),
(_______________________).
(2)已知DG//AB,若EC平分∠FED,求∠C的度数.
25.(本小题满分10分)
2021年6月5日是第50个“世界环境日”.为保护环境,某市公交公司计划购买A型和B
两种环保节能公交车共10辆.若购买A型公交车1辆,B型公交车2辆,共需400万元;若
购买A型公交车2辆,B型公交车1辆,共需350万元.
(1)求购买A型和B型公交车每辆各需多少万元?
(2)预计在某线路上A型和B型公交车每辆年均载客量分别为60万人次和100万人次.若该公司购买A型和B型公交车的总费用不超过1200万元,且确保这10辆公交车在该线路的年均载客总和不少于680万人次,则该公司有哪几种购车方案?
(3)在(2)的条件下,哪种购车方案总费用最少?最少总费用是多少万元?
26.(本小题满分10分)
如图1,在平面直角坐标系中,,且满足,过作轴于.
(1)求的面积.
(2)若过作交轴于,且分别平分,如图2,求的度数.
(3)在轴上存在点使得和的面积相等,请直接写出点坐标.
七年级数学答案
一、选择题(每小题3分,满分36分)
1.B 2.B 3.A 4.C 5.D 6.D 7.C 8.A 9.D 10.A 11.C 12.B
二、填空题(每小题3分,满分24分)
13. ﹣2 , ±6 14.①② 15.1 16(3,2)或(-3,-2)
17.或 18. 19.-2<a≤0 20.(0,-2)
三、解答题(满分60分)
21.(第(1)题4分,第(2)(3)小题每题6分,满分16分)
(1)
. -------4分
(2)
解:把3x-2y=4方程两边同时乘以3,得9x-6y=12③,
用②-③得9x-5y-9x+6y=13-12,
解得y=1,
把y=1代入①得3x-2×1=4,
解得x=2,
所以原方程组的解为
-------6分
(3)解:解不等式①,得,
解不等式②,得,
所以,不等式组的解集是, -----------4分
该不等式组的正整数解是1,2. -----------2分
22. (本小题满分6分)
解:(1)第二组的频率是=0.15
总篇数是18÷0.15=120(篇),
则本次活动共有120篇论文参加评比. -------2分
(2)由题意可知:从左至右各长方形的高的比为2:3:4:6:4:1,则从左到右的各组的频率为0.1、0.15、0.2、0.3、0.2、0.05,第四组的论文的频数=120×0.3=36篇,
则计算可知第四组上交的论文数量最多,有36篇. -------2分
(3)第六组的论文的频数=120×0.05=6篇;
第四组的获奖率=20÷36×100%≈56%,第六组的获奖率为4÷6≈67%;
56%<67%,
则第六组的获奖率较高. ---------2分
23.(本小题满分8分)
(1) -------2分
(2)(2,0);(-1,-1);(3,-2); ------每空1分
(3) ---------3分
24.(本小题满分10分)
解:(1)∵EF//DB(已知),
(两直线平行,同位角相等).
又∵∠1=∠2(已知),
∠D(等量代换),
(内错角相等,两直线平行); ----------每空2分
(2)∵DG∥AB,
∴∠D=∠2=50°,∠DEC=∠C,
∵BD∥EF,
∴∠DEF+∠D=180°,
∴∠DEF=130°,
∵平分∠DEF,
∴∠DEC=∠DEF=65°,
∴∠C=65°. --------3分
25.(本小题满分10分)
(1)设购买A型公交车每辆需x万元,购买B型公交车每辆需y万元,由题意得
,
解得. ------2分
答:购买A型公交车每辆需100万元,购买B型公交车每辆需150万元. ------1分
(2)设购买A型公交车a辆,则B型公交车(10﹣a)辆,由题意得
,
解得:6≤a≤8, -------2分
所以a=6,7,8;
则(10﹣a)=4,3,2; --------1分
三种方案:①购买A型公交车6辆,则B型公交车4辆;②购买A型公交车7辆,则B型公交车3辆;③购买A型公交车8辆,则B型公交车2辆; -------1分
(3)①购买A型公交车6辆,则B型公交车4辆:100×6+150×4=1200万元;
②购买A型公交车7辆,则B型公交车3辆:100×7+150×3=1150万元;
③购买A型公交车8辆,则B型公交车2辆:100×8+150×2=1100万元;
故购买A型公交车8辆,则B型公交车2辆费用最少,最少总费用为1100万元.---3分
26.(本小题满分10分)
解:(1)∵,,,
,,
∵,,,的面积;------4分
(2)解:∵CB//y轴,,,
又∵,∴,
过作,如图①,
∵BD//AC,,,
,分别平分,,即:,,
; -------4分
(3)或. -------每个1分
考生姓名
考生所在学校
准考证号
装
订
线
内
不
要
答
题
装
订
线
内
不
要
答
题
装
订
线
内
不
要
答
题
七年级数学试题 第1页(共8页)
七年级数学试题
题号 一 二 三 总分 核分人
21 22 23 24 25 26
得分
得分 评卷人
一、选择题(每小题3分,满分36分)
1.如图所示,由图案(1)平移得到的图案是( )
图(1) A B C D
2.在实数 ,, ,,,0中,无理数的个数为( )
A.1个 B.2个 C.3个 D.4个
3.不等式6-3x>0的解集在数轴上表示为( )
A. B.
C. D.
4.如图,10块相同的长方形墙砖拼成一个大长方形,设长方形墙砖的长和宽分别为x厘米和y厘米,则依题意所列方程组正确的是( )
A. B.
C. D.
5.如图,已知,,
平分,则( ).
A.32° B.60° C.58° D.64°
6.若是关于x、y的二元一次方程ax-5y=1的解,则a的值为( )
A. -5 B. -1 C. 9 D. 11
7.下列四个命题是真命题的是( )
A.两条直线被第三条直线所截,同位角相等
B. 互补的两个角一定是邻补角
C. 在同一平面内,垂直于同一条直线的两条直线互相平行
D. 相等的角是对顶角
8.在一个样本中,40个数据分别落在5个小组内,第1,2,3,5小组的频数分别是6,5,15,7,则第4小组的频数是( )
A. 7 B. 8 C. 9 D. 10
9.下列四个命题:①若a>b,则a-3>b-3;②若a>b,则a+c>b+c;③若a>b,则-3a<-3b;④若a>b,则ac>bc.其中,真命题有( )
A. ①③④ B②③④ C..①②③④ D.①②③
10.如图,直线AB,CD相交于点O,OA平分∠EOC,若∠EOC︰∠EOD=2︰3,则∠BOD的度数为( )
A.36° B.40° C.35° D.45°
(第10题) (第12题)
11.若方程组的解满足x+y>0,则m的取值范围是( )
A. m>-3 B. m>-2 C. m>-1 D. m>0
12.如图,现给出下列条件:①,②,③,④,⑤.其中能够得到AB//CD的条件的个数( )
A2个 B.3个 C.4个 D.5个
得分 评卷人
2、填空题(每小题3分,满分24分)
13.-8的立方根是_____,36的平方根是_____.
14.下列调查中,调查方式选择正确的是_____
①为了了解一批灯泡的使用寿命,选择抽样调查.②为了了解某公园全年的游客流量,选择抽样调查。③为了了解某1000枚炮弹的杀伤半径,选择全面调查。④为了了解一批袋装食品是否有防腐剂,选择全面调查。
15.在两个连续整数a和b之间,a<<b,那么b-a的值为_____.
16.点P(a,b)距离x轴2个单位长度,距离y轴3个单位长度且ab>0,则P点的坐标是 .
17.点为线段上一点,不与点、重合,于点,若,则的度数为 .
18.若方程是关于,的二元一次方程,则 .
19.若关于x的不等式2x-a≤4有3个非负整数解,则a的取值范围是 .
20.在平面直角坐标系中,对于点P(x,y),我们把点P′(-y+1,x+1)叫做点P的幸运点.已知点A1的幸运点为A2,点A2的幸运点为A3,点A3的幸运点为A4,……,这样依次得到点A1,A2,A3,…,An.若点A1的坐标为(3,1),则点A2020的坐标为 .
得分 评卷人
三、解答题(满分60分)
21.(第(1)题4分,第(2)(3)小题每题6分,满分16分)
(1)计算:.
(2)解方程组:
(3)解不等式组,并写出它的正整数解.
22.(本小题满分6分)
某市教育局在全市党员教职工中开展的“学党史,知党情,颂党恩”活动中,进行了论文的评比,论文的交稿时间为6月1日至25日,评委会把各校交的论文的篇数按4天一组分组统计,绘制成如图所示的频数分布直方图(每组包括左端点,不包括右端点)已知从左往右各小长方形的高的比为2:3:4:6:4:1,第二组的频数为18.请回答下列问题:
(1)本次活动共有多少篇论文参加评比
(2)哪组上交的论文数量最多 是多少
(3)经过评比,第四组和第六组分别有20篇、4篇论文获奖,则这两组哪组获奖率高
23.(本小题满分8分)
如图,三角形ABC在平面直角坐标系中第二象限内,顶点A的坐标是,先把三角形ABC向右平移4个单位,再向下平移3个单位得到三角形.
(1)请在图中作出三角形;
(2)点的坐标为_____;点的坐标为______;点的坐标为_____;
(3)求三角形的面积.
24.(本小题满分10分)
如图,已知.
(1)求证:
证明:∵EF//DB(已知)
(_____________________).
又∵∠1=∠2(已知),
___________(等量代换),
(_______________________).
(2)已知DG//AB,若EC平分∠FED,求∠C的度数.
25.(本小题满分10分)
2021年6月5日是第50个“世界环境日”.为保护环境,某市公交公司计划购买A型和B
两种环保节能公交车共10辆.若购买A型公交车1辆,B型公交车2辆,共需400万元;若
购买A型公交车2辆,B型公交车1辆,共需350万元.
(1)求购买A型和B型公交车每辆各需多少万元?
(2)预计在某线路上A型和B型公交车每辆年均载客量分别为60万人次和100万人次.若该公司购买A型和B型公交车的总费用不超过1200万元,且确保这10辆公交车在该线路的年均载客总和不少于680万人次,则该公司有哪几种购车方案?
(3)在(2)的条件下,哪种购车方案总费用最少?最少总费用是多少万元?
26.(本小题满分10分)
如图1,在平面直角坐标系中,,且满足,过作轴于.
(1)求的面积.
(2)若过作交轴于,且分别平分,如图2,求的度数.
(3)在轴上存在点使得和的面积相等,请直接写出点坐标.
七年级数学答案
一、选择题(每小题3分,满分36分)
1.B 2.B 3.A 4.C 5.D 6.D 7.C 8.A 9.D 10.A 11.C 12.B
二、填空题(每小题3分,满分24分)
13. ﹣2 , ±6 14.①② 15.1 16(3,2)或(-3,-2)
17.或 18. 19.-2<a≤0 20.(0,-2)
三、解答题(满分60分)
21.(第(1)题4分,第(2)(3)小题每题6分,满分16分)
(1)
. -------4分
(2)
解:把3x-2y=4方程两边同时乘以3,得9x-6y=12③,
用②-③得9x-5y-9x+6y=13-12,
解得y=1,
把y=1代入①得3x-2×1=4,
解得x=2,
所以原方程组的解为
-------6分
(3)解:解不等式①,得,
解不等式②,得,
所以,不等式组的解集是, -----------4分
该不等式组的正整数解是1,2. -----------2分
22. (本小题满分6分)
解:(1)第二组的频率是=0.15
总篇数是18÷0.15=120(篇),
则本次活动共有120篇论文参加评比. -------2分
(2)由题意可知:从左至右各长方形的高的比为2:3:4:6:4:1,则从左到右的各组的频率为0.1、0.15、0.2、0.3、0.2、0.05,第四组的论文的频数=120×0.3=36篇,
则计算可知第四组上交的论文数量最多,有36篇. -------2分
(3)第六组的论文的频数=120×0.05=6篇;
第四组的获奖率=20÷36×100%≈56%,第六组的获奖率为4÷6≈67%;
56%<67%,
则第六组的获奖率较高. ---------2分
23.(本小题满分8分)
(1) -------2分
(2)(2,0);(-1,-1);(3,-2); ------每空1分
(3) ---------3分
24.(本小题满分10分)
解:(1)∵EF//DB(已知),
(两直线平行,同位角相等).
又∵∠1=∠2(已知),
∠D(等量代换),
(内错角相等,两直线平行); ----------每空2分
(2)∵DG∥AB,
∴∠D=∠2=50°,∠DEC=∠C,
∵BD∥EF,
∴∠DEF+∠D=180°,
∴∠DEF=130°,
∵平分∠DEF,
∴∠DEC=∠DEF=65°,
∴∠C=65°. --------3分
25.(本小题满分10分)
(1)设购买A型公交车每辆需x万元,购买B型公交车每辆需y万元,由题意得
,
解得. ------2分
答:购买A型公交车每辆需100万元,购买B型公交车每辆需150万元. ------1分
(2)设购买A型公交车a辆,则B型公交车(10﹣a)辆,由题意得
,
解得:6≤a≤8, -------2分
所以a=6,7,8;
则(10﹣a)=4,3,2; --------1分
三种方案:①购买A型公交车6辆,则B型公交车4辆;②购买A型公交车7辆,则B型公交车3辆;③购买A型公交车8辆,则B型公交车2辆; -------1分
(3)①购买A型公交车6辆,则B型公交车4辆:100×6+150×4=1200万元;
②购买A型公交车7辆,则B型公交车3辆:100×7+150×3=1150万元;
③购买A型公交车8辆,则B型公交车2辆:100×8+150×2=1100万元;
故购买A型公交车8辆,则B型公交车2辆费用最少,最少总费用为1100万元.---3分
26.(本小题满分10分)
解:(1)∵,,,
,,
∵,,,的面积;------4分
(2)解:∵CB//y轴,,,
又∵,∴,
过作,如图①,
∵BD//AC,,,
,分别平分,,即:,,
; -------4分
(3)或. -------每个1分
考生姓名
考生所在学校
准考证号
装
订
线
内
不
要
答
题
装
订
线
内
不
要
答
题
装
订
线
内
不
要
答
题
七年级数学试题 第1页(共8页)
同课章节目录
