2021-2022学年华东师大新版九年级上册数学第24章 解直角三角形单元测试卷(word版含答案)
文档属性
| 名称 | 2021-2022学年华东师大新版九年级上册数学第24章 解直角三角形单元测试卷(word版含答案) |

|
|
| 格式 | zip | ||
| 文件大小 | 254.5KB | ||
| 资源类型 | 教案 | ||
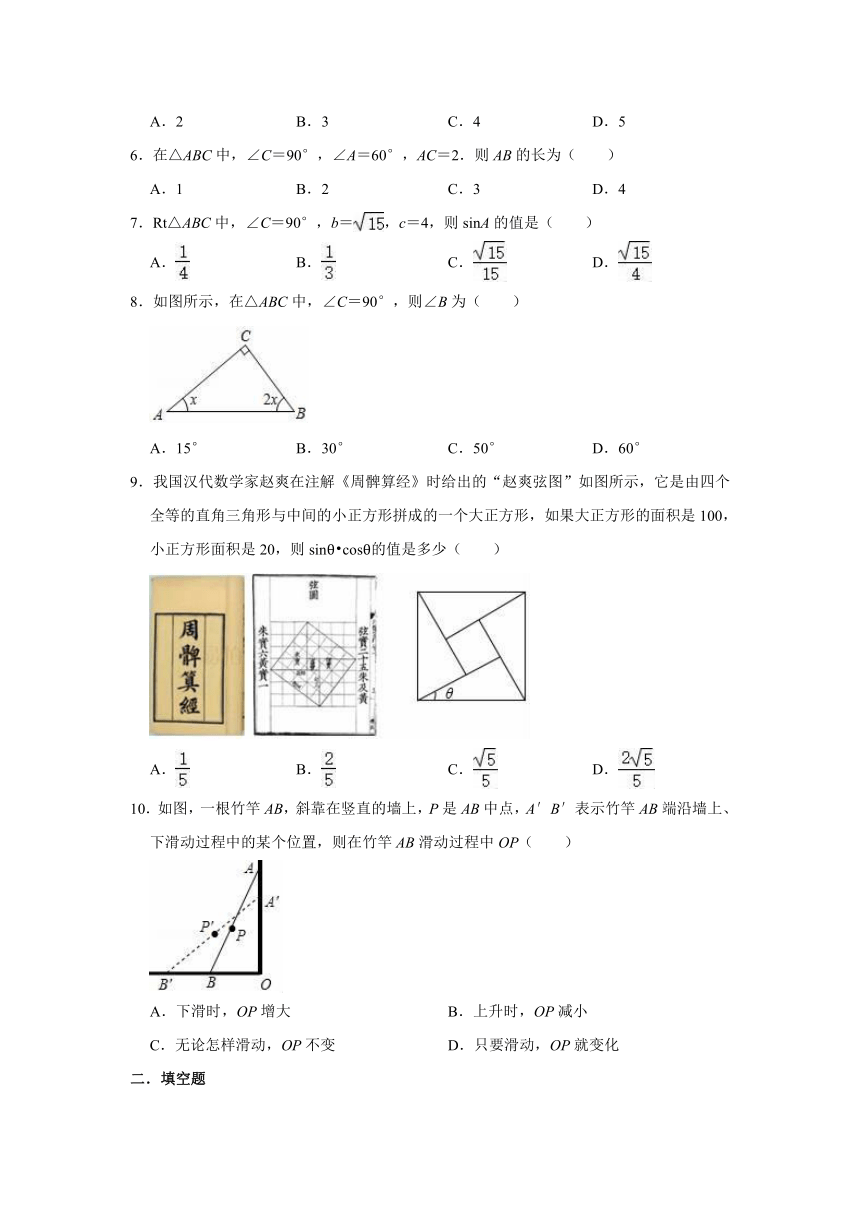
| 版本资源 | 华东师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-10-21 00:00:00 | ||
图片预览

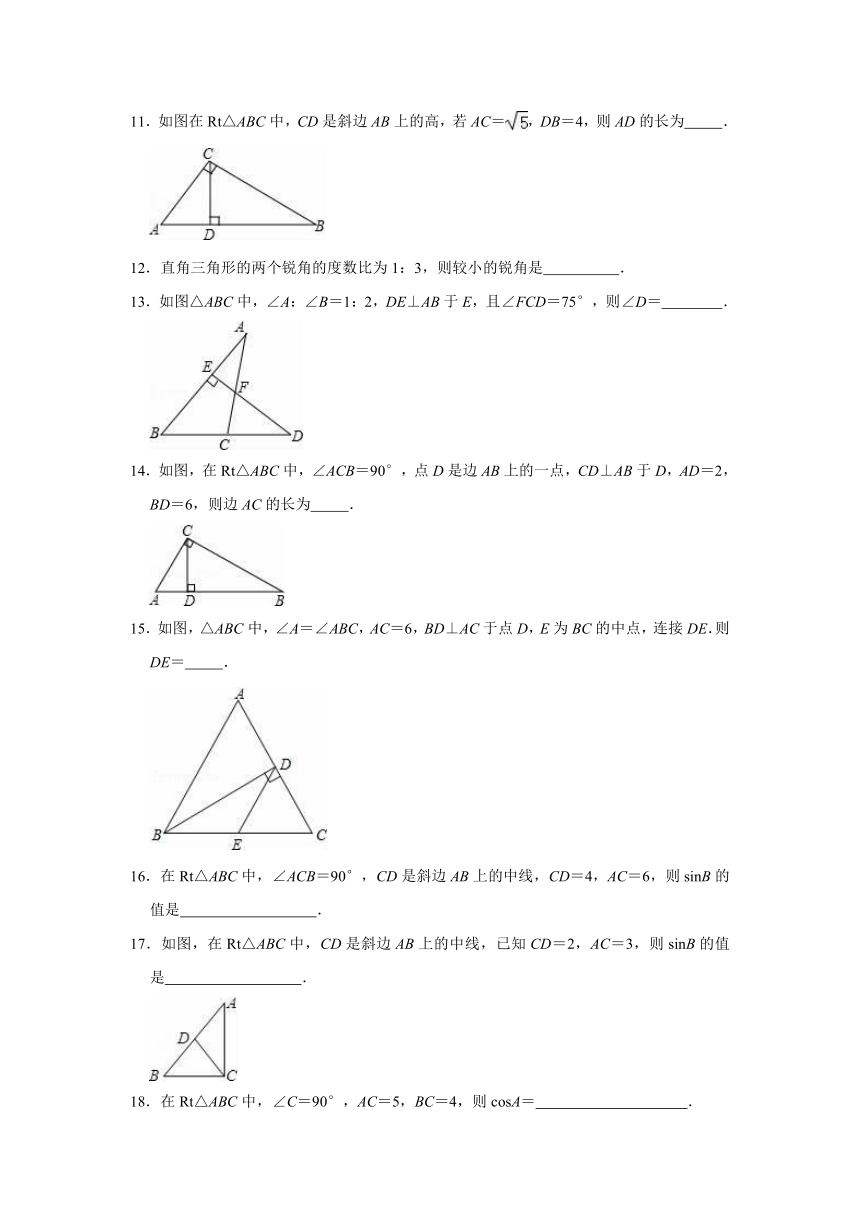
文档简介
2021-2022学年华东师大新版九年级上册数学《第24章 解直角三角形》单元测试卷
一.选择题
1.如图,在Rt△ABC中,∠ACB=90°,CD⊥AB于D,若AD=1,BD=4,则CD=( )
A.2 B.4 C. D.3
2.在Rt△ABC中,∠C=90°,∠A=70°,则∠B的度数为( )
A.20° B.30° C.40° D.70°
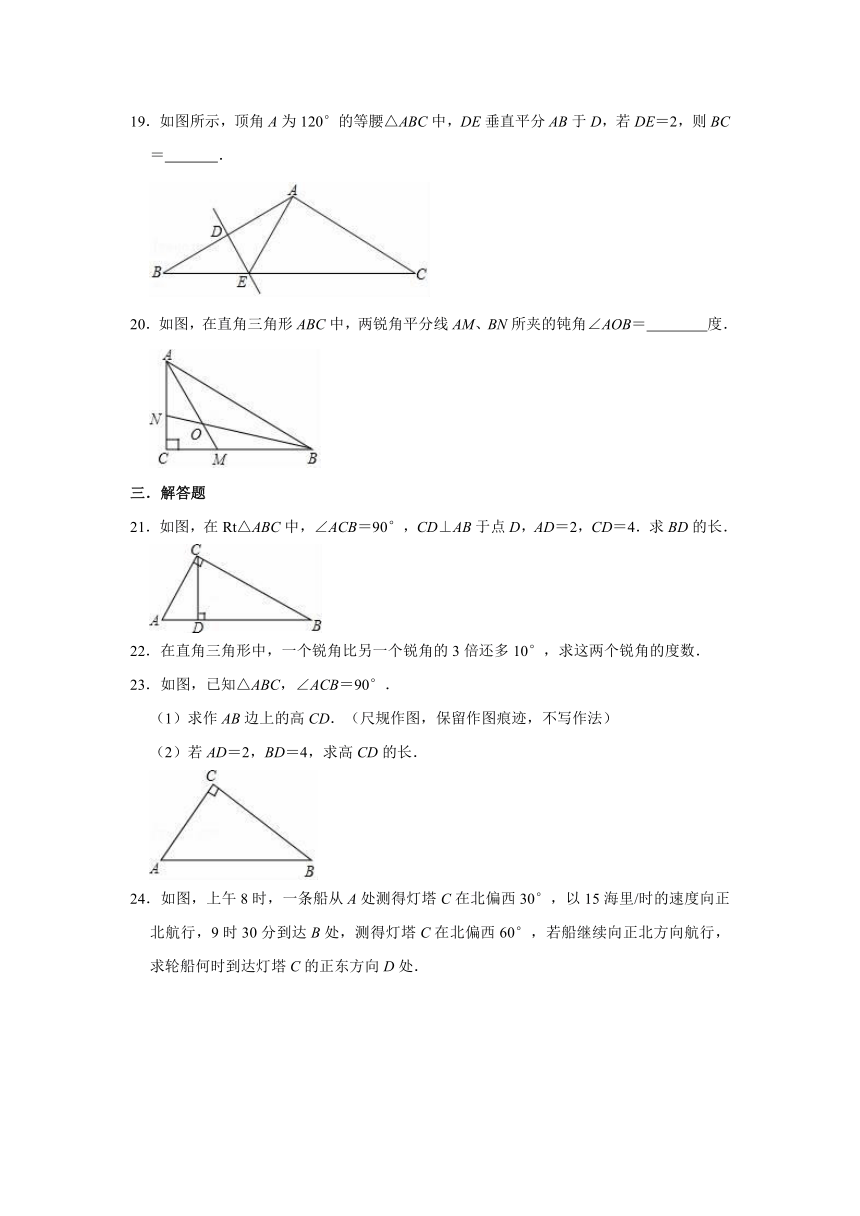
3.下列说法中,正确的有( )
①有一个角为60°的等腰三角形是等边三角形
②三边分别是1,,3的三角形是直角三角形
③一边上的中线等于这条边的一半的三角形是直角三角形
④三个角之比为3:4:5的三角形是直角三角形
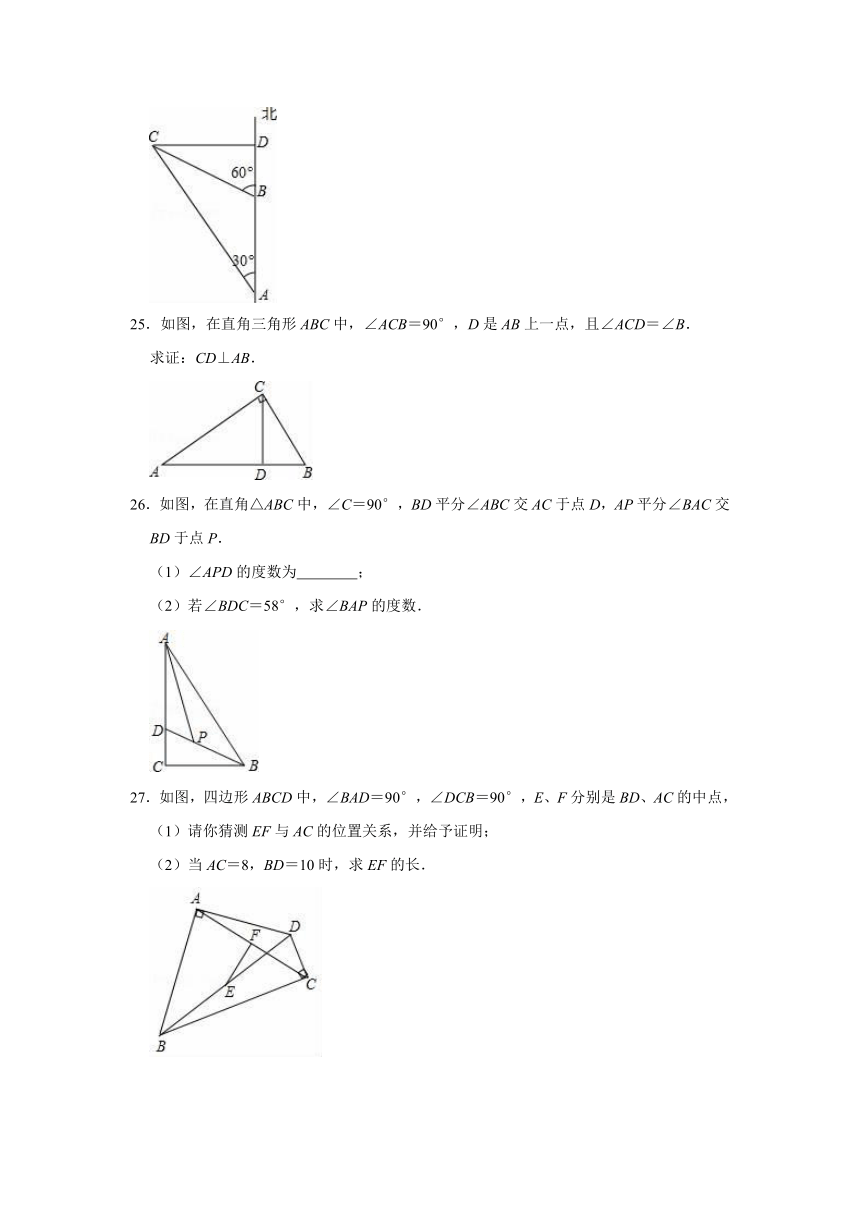
A.1个 B.2个 C.3个 D.4个
4.如图,在边长为1的小正方形组成的网格中,△ABC的三个顶点均在格点上,则tan∠ABC的值为( )
A. B. C. D.1
5.如图,在Rt△ABC中,∠ACB=90°,CD是AB边上的高,AC=6,AB=9,则AD=( )
A.2 B.3 C.4 D.5
6.在△ABC中,∠C=90°,∠A=60°,AC=2.则AB的长为( )
A.1 B.2 C.3 D.4
7.Rt△ABC中,∠C=90°,b=,c=4,则sinA的值是( )
A. B. C. D.
8.如图所示,在△ABC中,∠C=90°,则∠B为( )
A.15° B.30° C.50° D.60°
9.我国汉代数学家赵爽在注解《周髀算经》时给出的“赵爽弦图”如图所示,它是由四个全等的直角三角形与中间的小正方形拼成的一个大正方形,如果大正方形的面积是100,小正方形面积是20,则sinθ cosθ的值是多少( )
A. B. C. D.
10.如图,一根竹竿AB,斜靠在竖直的墙上,P是AB中点,A′B′表示竹竿AB端沿墙上、下滑动过程中的某个位置,则在竹竿AB滑动过程中OP( )
A.下滑时,OP增大 B.上升时,OP减小
C.无论怎样滑动,OP不变 D.只要滑动,OP就变化
二.填空题
11.如图在Rt△ABC中,CD是斜边AB上的高,若AC=,DB=4,则AD的长为 .
12.直角三角形的两个锐角的度数比为1:3,则较小的锐角是 .
13.如图△ABC中,∠A:∠B=1:2,DE⊥AB于E,且∠FCD=75°,则∠D= .
14.如图,在Rt△ABC中,∠ACB=90°,点D是边AB上的一点,CD⊥AB于D,AD=2,BD=6,则边AC的长为 .
15.如图,△ABC中,∠A=∠ABC,AC=6,BD⊥AC于点D,E为BC的中点,连接DE.则DE= .
16.在Rt△ABC中,∠ACB=90°,CD是斜边AB上的中线,CD=4,AC=6,则sinB的值是 .
17.如图,在Rt△ABC中,CD是斜边AB上的中线,已知CD=2,AC=3,则sinB的值是 .
18.在Rt△ABC中,∠C=90°,AC=5,BC=4,则cosA= .
19.如图所示,顶角A为120°的等腰△ABC中,DE垂直平分AB于D,若DE=2,则BC= .
20.如图,在直角三角形ABC中,两锐角平分线AM、BN所夹的钝角∠AOB= 度.
三.解答题
21.如图,在Rt△ABC中,∠ACB=90°,CD⊥AB于点D,AD=2,CD=4.求BD的长.
22.在直角三角形中,一个锐角比另一个锐角的3倍还多10°,求这两个锐角的度数.
23.如图,已知△ABC,∠ACB=90°.
(1)求作AB边上的高CD.(尺规作图,保留作图痕迹,不写作法)
(2)若AD=2,BD=4,求高CD的长.
24.如图,上午8时,一条船从A处测得灯塔C在北偏西30°,以15海里/时的速度向正北航行,9时30分到达B处,测得灯塔C在北偏西60°,若船继续向正北方向航行,求轮船何时到达灯塔C的正东方向D处.
25.如图,在直角三角形ABC中,∠ACB=90°,D是AB上一点,且∠ACD=∠B.
求证:CD⊥AB.
26.如图,在直角△ABC中,∠C=90°,BD平分∠ABC交AC于点D,AP平分∠BAC交BD于点P.
(1)∠APD的度数为 ;
(2)若∠BDC=58°,求∠BAP的度数.
27.如图,四边形ABCD中,∠BAD=90°,∠DCB=90°,E、F分别是BD、AC的中点,
(1)请你猜测EF与AC的位置关系,并给予证明;
(2)当AC=8,BD=10时,求EF的长.
参考答案与试题解析
一.选择题
1.解:∵∠ACB=90°,CD⊥AB于D,
∴CD2=AD BD=1×4=4,
∴CD=2.
故选:A.
2.解:
∵在Rt△ABC中,∠C=90°,
∴∠A+∠B=90°,
∴∠B=90°﹣∠A=90°﹣70°=20°,
故选:A.
3.解:①正确,符合等边三角形的判定定理;
②正确,因为12+32=()2,所以三边分别是1,,3的三角形是直角三角形;
③正确,根据矩形对角线的性质的逆命题;
④错误,三边之比为3:4:5的三角形是直角三角形.
故选:C.
4.解:如图,在直角△ABD中,AD=3,BD=4,
则tan∠ABC==.
故选:B.
5.解:∵Rt△ABC中,∠ACB=90°,CD是AB边上的高,
∴AC2=AD AB,
∵AC=6,AB=9,
∴36=9AD,
则AD=4.
故选:C.
6.解:∵∠C=90°,∠A=60°,
∴∠B=90°﹣∠A=30°,
∵AC=2,
∴AB=2AC=4.
故选:D.
7.解:如图,AC=b=,AB=c=4,
所以BC=a==1,
由三角函数的定义可得sinA==,
则sinA=,
故选:A.
8.解:如图所示,在△ABC中,∠C=90°,则x+2x=90°.
x=30°.
所以2x=60°,即∠B为60°.
故选:D.
9.解:∵大正方形的面积是100,小正方形面积是20,
∴大正方形的边长为10,小正方形的边长为2,
∴10cosθ﹣10sinθ=2,
∴cosθ﹣sinθ=,
∴(sinθ﹣cosθ)2=,
sin2θ﹣2sinθ cosθ+cos2θ=,
1﹣2sinθ cosθ=,
sinθ cosθ=.
故选:B.
10.解:∵AO⊥BO,点P是AB的中点,
∴OP=AB,
∴在滑动的过程中OP的长度不变.
故选:C.
二.填空题
11.解:由射影定理得,AC2=AD AB,
则()2=AD×(AD+4),
解得,AD1=1,AD2=﹣5(舍去),
故答案为:1.
12.解:设两个锐角度数为x°,3x°,
由题意得:x+3x=90,
解得:x=22.5,
∴较小的锐角是22.5°.
故答案为:22.5°.
13.解:∵∠FCD=75°,
∴∠A+∠B=75°,
∵∠A:∠B=1:2,
∴∠A=×75°=25°,
∵DE⊥AB于E,
∴∠AFE=90°﹣∠A=90°﹣25°=65°,
∴∠CFD=∠AFE=65°,
∵∠FCD=75°,
∴∠D=180°﹣∠CFD﹣∠FCD=180°﹣65°﹣75°=40°.
故答案为:40°
14.解:由射影定理得,AC2=AD AB=2×(2+6),
解得,AC=4,
故答案为:4.
15.解:∵△ABC中,∠A=∠ABC,AC=6,
∴AC=BC=6.
又E为BC的中点,
∴DE=BC=3.
故答案是:3.
16.解:∵Rt△ABC中,CD是斜边AB上的中线,CD=4,
∴AB=2CD=8,
则sinB===.
故答案为:.
17.解:∵Rt△ABC中,CD是斜边AB上的中线,CD=2,
∴AB=2CD=4,
则sinB==.
故答案为:.
18.解:在Rt△ABC中,
∵∠C=90°,AC=5,BC=4,
∴AB=,
∴cosA===,
故答案为.
19.解:∵AB=AC,∠A=120°,
∴∠B=∠C=30°,
∵DE垂直平分AB,
∴BE=AE,
∴∠B=∠BAE=30°,
∴∠EAC=90°,
∴AE=CE=2DE=4,
∴CE=2AE=8,
∴BC=BE+CE=8+4=12,
故答案为:12.
20.解:∵△ABC是直角三角形,
∴∠BAC+∠ABC=90°,
又∵AM,BN为∠BAC,∠ABC的角平分线,
∴∠CAM+∠NBC=45°,
∴∠AOB=180°﹣(∠CAM+∠NBC)=135°,
∴∠AOB=135°.
故答案为:135
三.解答题
21.解:∵在Rt△ABC中,∠ACB=90°,CD⊥AB,
∴∠CDB=∠ACB=90°,
∴∠ACD+∠BCD=90°,∠BCD+∠B=90°,
∴∠ACD=∠B,
∴△ACD∽△CBD,
∴=,
∵AD=2,CD=4,
∴=,
∴BD=8.
22.解:设另一个锐角为x°,则一个锐角为(3x+10)°,
由题意得,x+(3x+10)=90,
解得x=20,
3x+10=3×20+10=70,
所以,这两个锐角的度数分别为20°,70°.
23.解:(1)如图所示,CD即为所求;
(2)∵CD⊥AB,∠ACB=90°,
∴CD2=AD DB,
∵AD=2,DB=4,
∴CD=2.
24.解:∵∠CBD为△ABC的外角,∠CBD=60°,∠CAB=30°,
∴∠ACB=∠CBD﹣∠CAB=30°,
∴∠CAB=∠ACB,
AB=15×(9.5﹣8)=22.5,
∴AB=BC=22.5,
在Rt△BCD中,∠BCD=30°,
∴BD=BC=11.25,
∴从B到D用的时间为11.25÷15=小时=45分钟,
则当船继续航行,10时15分到达灯塔C在正东方向.
25.证明:∵∠ACB=90°,
∴∠A+∠B=90°,
∵∠ACD=∠B,
∴∠A+∠ACD=90°,
∴∠ADC=90°,
∴CD⊥AB.
26.解:(1)∵∠C=90°,
∴∠ABC+∠BAC=90°,
∴(∠BAC+∠ABC)=45°.
∵BD平分∠ABC,AP平分∠BAC,
∴∠BAP+∠ABP=∠BAC+∠ABC=(∠BAC+∠ABC)=45°.
∴∠APD=∠BAP+∠ABP=45°;
故答案为45°.
(2)∵∠BDC=58°,
∴∠DBC=90°﹣∠BDC=32°,
∵BD平分∠ABC,
∴∠ABD=∠DBC=32°,
∴∠BAP=∠APD﹣∠ABD=45°﹣32°=13°.
27.解:(1)EF⊥AC.理由如下:
连接AE、CE,
∵∠BAD=90°,E为BD中点,
∴AE=DB,
∵∠DCB=90°,
∴CE=BD,
∴AE=CE,
∵F是AC中点,
∴EF⊥AC;
(2)∵AC=8,BD=10,E、F分别是边AC、BD的中点,
∴AE=CE=5,CF=4,
∵EF⊥AC.
∴EF===3
一.选择题
1.如图,在Rt△ABC中,∠ACB=90°,CD⊥AB于D,若AD=1,BD=4,则CD=( )
A.2 B.4 C. D.3
2.在Rt△ABC中,∠C=90°,∠A=70°,则∠B的度数为( )
A.20° B.30° C.40° D.70°
3.下列说法中,正确的有( )
①有一个角为60°的等腰三角形是等边三角形
②三边分别是1,,3的三角形是直角三角形
③一边上的中线等于这条边的一半的三角形是直角三角形
④三个角之比为3:4:5的三角形是直角三角形
A.1个 B.2个 C.3个 D.4个
4.如图,在边长为1的小正方形组成的网格中,△ABC的三个顶点均在格点上,则tan∠ABC的值为( )
A. B. C. D.1
5.如图,在Rt△ABC中,∠ACB=90°,CD是AB边上的高,AC=6,AB=9,则AD=( )
A.2 B.3 C.4 D.5
6.在△ABC中,∠C=90°,∠A=60°,AC=2.则AB的长为( )
A.1 B.2 C.3 D.4
7.Rt△ABC中,∠C=90°,b=,c=4,则sinA的值是( )
A. B. C. D.
8.如图所示,在△ABC中,∠C=90°,则∠B为( )
A.15° B.30° C.50° D.60°
9.我国汉代数学家赵爽在注解《周髀算经》时给出的“赵爽弦图”如图所示,它是由四个全等的直角三角形与中间的小正方形拼成的一个大正方形,如果大正方形的面积是100,小正方形面积是20,则sinθ cosθ的值是多少( )
A. B. C. D.
10.如图,一根竹竿AB,斜靠在竖直的墙上,P是AB中点,A′B′表示竹竿AB端沿墙上、下滑动过程中的某个位置,则在竹竿AB滑动过程中OP( )
A.下滑时,OP增大 B.上升时,OP减小
C.无论怎样滑动,OP不变 D.只要滑动,OP就变化
二.填空题
11.如图在Rt△ABC中,CD是斜边AB上的高,若AC=,DB=4,则AD的长为 .
12.直角三角形的两个锐角的度数比为1:3,则较小的锐角是 .
13.如图△ABC中,∠A:∠B=1:2,DE⊥AB于E,且∠FCD=75°,则∠D= .
14.如图,在Rt△ABC中,∠ACB=90°,点D是边AB上的一点,CD⊥AB于D,AD=2,BD=6,则边AC的长为 .
15.如图,△ABC中,∠A=∠ABC,AC=6,BD⊥AC于点D,E为BC的中点,连接DE.则DE= .
16.在Rt△ABC中,∠ACB=90°,CD是斜边AB上的中线,CD=4,AC=6,则sinB的值是 .
17.如图,在Rt△ABC中,CD是斜边AB上的中线,已知CD=2,AC=3,则sinB的值是 .
18.在Rt△ABC中,∠C=90°,AC=5,BC=4,则cosA= .
19.如图所示,顶角A为120°的等腰△ABC中,DE垂直平分AB于D,若DE=2,则BC= .
20.如图,在直角三角形ABC中,两锐角平分线AM、BN所夹的钝角∠AOB= 度.
三.解答题
21.如图,在Rt△ABC中,∠ACB=90°,CD⊥AB于点D,AD=2,CD=4.求BD的长.
22.在直角三角形中,一个锐角比另一个锐角的3倍还多10°,求这两个锐角的度数.
23.如图,已知△ABC,∠ACB=90°.
(1)求作AB边上的高CD.(尺规作图,保留作图痕迹,不写作法)
(2)若AD=2,BD=4,求高CD的长.
24.如图,上午8时,一条船从A处测得灯塔C在北偏西30°,以15海里/时的速度向正北航行,9时30分到达B处,测得灯塔C在北偏西60°,若船继续向正北方向航行,求轮船何时到达灯塔C的正东方向D处.
25.如图,在直角三角形ABC中,∠ACB=90°,D是AB上一点,且∠ACD=∠B.
求证:CD⊥AB.
26.如图,在直角△ABC中,∠C=90°,BD平分∠ABC交AC于点D,AP平分∠BAC交BD于点P.
(1)∠APD的度数为 ;
(2)若∠BDC=58°,求∠BAP的度数.
27.如图,四边形ABCD中,∠BAD=90°,∠DCB=90°,E、F分别是BD、AC的中点,
(1)请你猜测EF与AC的位置关系,并给予证明;
(2)当AC=8,BD=10时,求EF的长.
参考答案与试题解析
一.选择题
1.解:∵∠ACB=90°,CD⊥AB于D,
∴CD2=AD BD=1×4=4,
∴CD=2.
故选:A.
2.解:
∵在Rt△ABC中,∠C=90°,
∴∠A+∠B=90°,
∴∠B=90°﹣∠A=90°﹣70°=20°,
故选:A.
3.解:①正确,符合等边三角形的判定定理;
②正确,因为12+32=()2,所以三边分别是1,,3的三角形是直角三角形;
③正确,根据矩形对角线的性质的逆命题;
④错误,三边之比为3:4:5的三角形是直角三角形.
故选:C.
4.解:如图,在直角△ABD中,AD=3,BD=4,
则tan∠ABC==.
故选:B.
5.解:∵Rt△ABC中,∠ACB=90°,CD是AB边上的高,
∴AC2=AD AB,
∵AC=6,AB=9,
∴36=9AD,
则AD=4.
故选:C.
6.解:∵∠C=90°,∠A=60°,
∴∠B=90°﹣∠A=30°,
∵AC=2,
∴AB=2AC=4.
故选:D.
7.解:如图,AC=b=,AB=c=4,
所以BC=a==1,
由三角函数的定义可得sinA==,
则sinA=,
故选:A.
8.解:如图所示,在△ABC中,∠C=90°,则x+2x=90°.
x=30°.
所以2x=60°,即∠B为60°.
故选:D.
9.解:∵大正方形的面积是100,小正方形面积是20,
∴大正方形的边长为10,小正方形的边长为2,
∴10cosθ﹣10sinθ=2,
∴cosθ﹣sinθ=,
∴(sinθ﹣cosθ)2=,
sin2θ﹣2sinθ cosθ+cos2θ=,
1﹣2sinθ cosθ=,
sinθ cosθ=.
故选:B.
10.解:∵AO⊥BO,点P是AB的中点,
∴OP=AB,
∴在滑动的过程中OP的长度不变.
故选:C.
二.填空题
11.解:由射影定理得,AC2=AD AB,
则()2=AD×(AD+4),
解得,AD1=1,AD2=﹣5(舍去),
故答案为:1.
12.解:设两个锐角度数为x°,3x°,
由题意得:x+3x=90,
解得:x=22.5,
∴较小的锐角是22.5°.
故答案为:22.5°.
13.解:∵∠FCD=75°,
∴∠A+∠B=75°,
∵∠A:∠B=1:2,
∴∠A=×75°=25°,
∵DE⊥AB于E,
∴∠AFE=90°﹣∠A=90°﹣25°=65°,
∴∠CFD=∠AFE=65°,
∵∠FCD=75°,
∴∠D=180°﹣∠CFD﹣∠FCD=180°﹣65°﹣75°=40°.
故答案为:40°
14.解:由射影定理得,AC2=AD AB=2×(2+6),
解得,AC=4,
故答案为:4.
15.解:∵△ABC中,∠A=∠ABC,AC=6,
∴AC=BC=6.
又E为BC的中点,
∴DE=BC=3.
故答案是:3.
16.解:∵Rt△ABC中,CD是斜边AB上的中线,CD=4,
∴AB=2CD=8,
则sinB===.
故答案为:.
17.解:∵Rt△ABC中,CD是斜边AB上的中线,CD=2,
∴AB=2CD=4,
则sinB==.
故答案为:.
18.解:在Rt△ABC中,
∵∠C=90°,AC=5,BC=4,
∴AB=,
∴cosA===,
故答案为.
19.解:∵AB=AC,∠A=120°,
∴∠B=∠C=30°,
∵DE垂直平分AB,
∴BE=AE,
∴∠B=∠BAE=30°,
∴∠EAC=90°,
∴AE=CE=2DE=4,
∴CE=2AE=8,
∴BC=BE+CE=8+4=12,
故答案为:12.
20.解:∵△ABC是直角三角形,
∴∠BAC+∠ABC=90°,
又∵AM,BN为∠BAC,∠ABC的角平分线,
∴∠CAM+∠NBC=45°,
∴∠AOB=180°﹣(∠CAM+∠NBC)=135°,
∴∠AOB=135°.
故答案为:135
三.解答题
21.解:∵在Rt△ABC中,∠ACB=90°,CD⊥AB,
∴∠CDB=∠ACB=90°,
∴∠ACD+∠BCD=90°,∠BCD+∠B=90°,
∴∠ACD=∠B,
∴△ACD∽△CBD,
∴=,
∵AD=2,CD=4,
∴=,
∴BD=8.
22.解:设另一个锐角为x°,则一个锐角为(3x+10)°,
由题意得,x+(3x+10)=90,
解得x=20,
3x+10=3×20+10=70,
所以,这两个锐角的度数分别为20°,70°.
23.解:(1)如图所示,CD即为所求;
(2)∵CD⊥AB,∠ACB=90°,
∴CD2=AD DB,
∵AD=2,DB=4,
∴CD=2.
24.解:∵∠CBD为△ABC的外角,∠CBD=60°,∠CAB=30°,
∴∠ACB=∠CBD﹣∠CAB=30°,
∴∠CAB=∠ACB,
AB=15×(9.5﹣8)=22.5,
∴AB=BC=22.5,
在Rt△BCD中,∠BCD=30°,
∴BD=BC=11.25,
∴从B到D用的时间为11.25÷15=小时=45分钟,
则当船继续航行,10时15分到达灯塔C在正东方向.
25.证明:∵∠ACB=90°,
∴∠A+∠B=90°,
∵∠ACD=∠B,
∴∠A+∠ACD=90°,
∴∠ADC=90°,
∴CD⊥AB.
26.解:(1)∵∠C=90°,
∴∠ABC+∠BAC=90°,
∴(∠BAC+∠ABC)=45°.
∵BD平分∠ABC,AP平分∠BAC,
∴∠BAP+∠ABP=∠BAC+∠ABC=(∠BAC+∠ABC)=45°.
∴∠APD=∠BAP+∠ABP=45°;
故答案为45°.
(2)∵∠BDC=58°,
∴∠DBC=90°﹣∠BDC=32°,
∵BD平分∠ABC,
∴∠ABD=∠DBC=32°,
∴∠BAP=∠APD﹣∠ABD=45°﹣32°=13°.
27.解:(1)EF⊥AC.理由如下:
连接AE、CE,
∵∠BAD=90°,E为BD中点,
∴AE=DB,
∵∠DCB=90°,
∴CE=BD,
∴AE=CE,
∵F是AC中点,
∴EF⊥AC;
(2)∵AC=8,BD=10,E、F分别是边AC、BD的中点,
∴AE=CE=5,CF=4,
∵EF⊥AC.
∴EF===3
