2021-2022学年华东师大新版七年级上册数学《第4章 图形的初步认识》单元测试卷(有答案)
文档属性
| 名称 | 2021-2022学年华东师大新版七年级上册数学《第4章 图形的初步认识》单元测试卷(有答案) |  | |
| 格式 | zip | ||
| 文件大小 | 230.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 华东师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-10-20 15:34:55 | ||
图片预览




文档简介
2021-2022学年华东师大新版七年级上册数学《第4章 图形的初步认识》单元测试卷
一.选择题
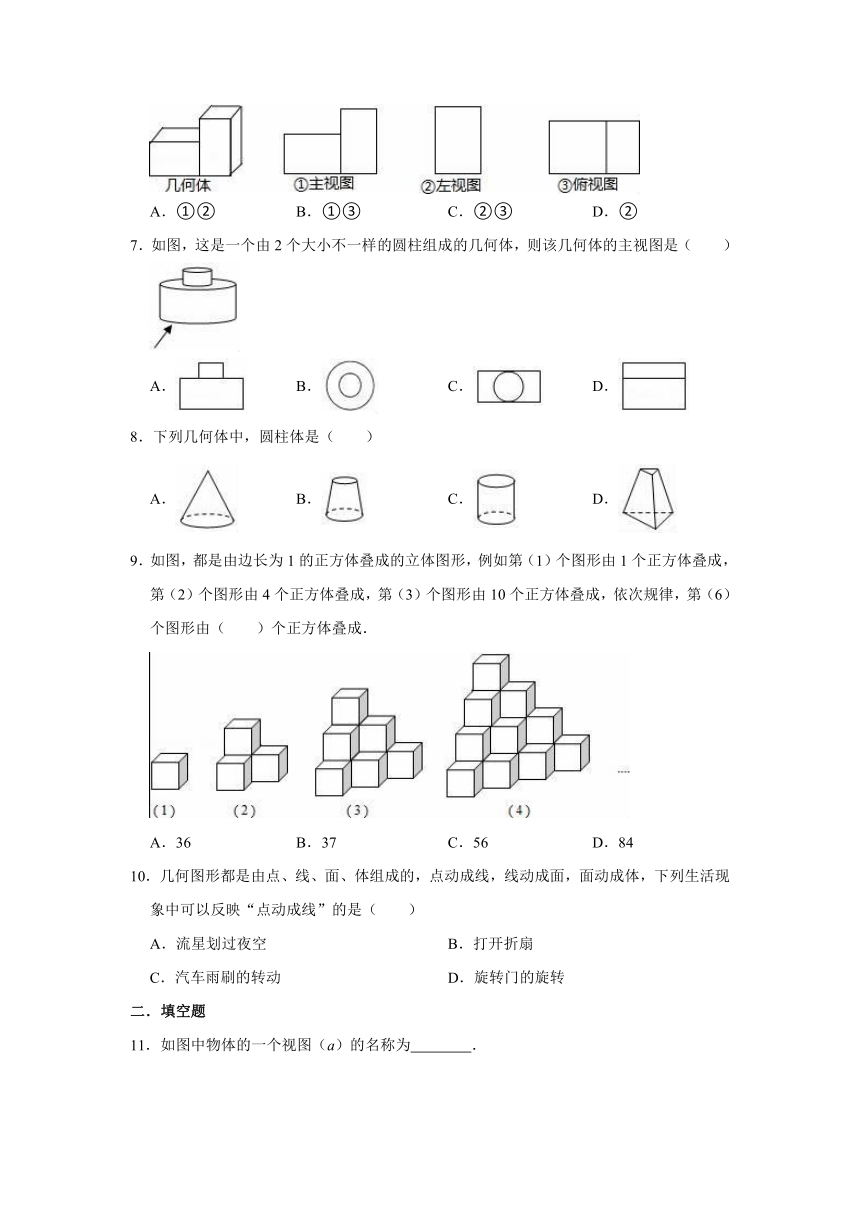
1.下列几何体没有曲面的是( )
A.圆柱 B.圆锥 C.球 D.长方体
2.一个六棱柱模型如图所示,底面边长都是5cm,侧棱长为4cm,这个六棱柱的所有侧面的面积之和是( )
A.20cm2 B.60cm2 C.120cm2 D.240cm2
3.下列几何体中,正视图、左视图和俯视图完全相同的是( )
A.圆锥 B.长方体
C.圆柱 D.正方体
4.如图是一个圆柱体,则它的主视图是( )
A. B. C. D.
5.如图立体图形中,三视图都一样的是( )
A. B. C. D.
6.某同学画出了如图所示的几何体的三种视图,其中正确的是( )
A.①② B.①③ C.②③ D.②
7.如图,这是一个由2个大小不一样的圆柱组成的几何体,则该几何体的主视图是( )
A. B. C. D.
8.下列几何体中,圆柱体是( )
A. B. C. D.
9.如图,都是由边长为1的正方体叠成的立体图形,例如第(1)个图形由1个正方体叠成,第(2)个图形由4个正方体叠成,第(3)个图形由10个正方体叠成,依次规律,第(6)个图形由( )个正方体叠成.
A.36 B.37 C.56 D.84
10.几何图形都是由点、线、面、体组成的,点动成线,线动成面,面动成体,下列生活现象中可以反映“点动成线”的是( )
A.流星划过夜空 B.打开折扇
C.汽车雨刷的转动 D.旋转门的旋转
二.填空题
11.如图中物体的一个视图(a)的名称为 .
12.如图,由四个小正方体组成的几何体中,若每个小正方体的棱长都是1,则该几何体俯视图的面积是 .
13.一个棱柱有18条棱,则这个棱柱共有 个面.
14.一个三棱柱有 个顶点, 条棱.
15.一个棱柱共有15条棱,那么它是 棱柱,有 个面.
16.一桶油漆可刷的面积为1500dm2,小明用这桶油漆恰好刷完10个同样的正方体形状的盒子的全部外表面,则此正方体盒子的棱长是 dm.
17.请将六棱柱的三视图名称依次填在横线上 .
18.在①正方体、②球、③圆锥、④圆柱、⑤三棱柱这五种几何体中,其主视图、左视图、俯视图都完全相同的是 .
19.把三角板绕着一条直角边旋转一圈,则所围成的几何体是 .
20.如图,是由一些大小相同的小正方体组合成的简单几何体
(1)图中有 块小正方体;
(2)该几何体的主视图如图所示,请在下面方格纸中分别画出它的左视图和俯视图.
三.解答题
21.两个圆柱体容器如图所示,容器1的半径是4cm,高是20cm;容器2的半径是6cm,高是8cm,我们先在容器2中倒满水,然后将里面的水全部倒入容器1中,问:倒完以后,容器1中的水面离容器口有多少厘米?
22.如图所示是一张铁皮.
(1)计算该铁皮的面积;
(2)它能否做成一个长方体盒子?若能,画出来,计算它的体积;若不能,说明理由.
23.台州奉化一果农有一批经过挑选的橙子要包装出售,现随意挑选10个,橙子测量直径,数据分别为(单位:cm)7.9,7.8,8,7.9,8,8,7.9,7.9,7.8,7.8.橙子内包装模型的横截面如图(1),凹型为半圆形,半圆的直径为这批橙子大约平均值加0.2cm,现用纸箱作外包装,内包装嵌入纸箱内,每箱装一层,一层装5×4个如图(2)所示,纸箱的高度比内包装高5cm.
(1)估计这批橙子的平均直径大约是多少?
(2)设计纸箱(不加盖子)的长、宽、高各为多少?(数据保留整数,设计时长和宽比内包装各需加长0.5cm).
(3)加工成一只纸箱的硬纸板面积较合理需多少cm2,请给出一种方案.(不计接头重叠部分,盖子顶面用透明纸)
24.如图是由7个完全相同的小立方块搭成的几何体,请画出它的三视图.
25.如图四个几何体分别是三棱柱,四棱柱,五棱柱和六棱柱,三棱柱有5个面,9条棱,6个顶点,观察图形,填写下面的空.
(1)四棱柱有 个面, 条棱, 个顶点;
(2)六棱柱有 个面, 条棱, 个顶点;
(3)由此猜想n棱柱有 个面, 条棱, 个顶点.
26.用数学的眼光去观察问题,你会发现很多图形都能看成是动静结合,舒展自如的.下面所给的三排图形都存在着某种联系,用线将它们连起来.
27.由几个相同的边长为1的小立方块搭成的几何体的俯视图如下图,格中的数字表示该位置的小立方块的个数.
(1)请在下面方格纸中分别画出这个向何体的主视图和左视图.
(2)根据三视图;这个组合几何体的表面积为 个平方单位.(包括底面积)
(3)若上述小立方块搭成的几何体的俯视图不变,各位置的小立方块个数可以改变(总数目不变),则搭成这样的组合几何体中的表面积最大是为 个平方单位.(包括底面积)
参考答案与试题解析
一.选择题
1.解:A、圆柱由2个平面和一个曲面组成,不符合题意;
B、圆锥由一个平面和一个曲面组成,不符合题意;
C、球由一个曲面组成,不符合题意;
D、长方体是由六个平面组成,符合题意.
故选:D.
2.解:六棱柱的侧面积为:4×5×6=120(cm2).
故选:C.
3.解:A、圆锥的正视图为三角形,左视图为三角形,俯视图为含有直径的圆,故本选项错误;
B、长方体的正视图为矩形,左视图为矩形,俯视图为矩形,但三个矩形的形状不一样,故本选项错误;
C、圆柱的正视图为矩形,左视图为距形,俯视图为圆,故本选项错误;
D、正方形的正视图为正方形,主视图为正方形,俯视图为正方形,故本选项正确;
故选:D.
4.解:一个直立在水平面上的圆柱体的主视图是长方形,
故选:A.
5.解:A、圆柱的主视图和左视图是矩形,俯视图是圆,故本选项不合题意;
B、圆锥的主视图和左视图是三角形,俯视图是带有圆心的圆,故本选项不合题意;
C、立方体的三视图都是正方形,故本选项符合题意;
D、三棱柱的主视图和俯视图是矩形,左视图是三角形,故本选项不合题意.
故选:C.
6.解:根据几何体的摆放位置,主视图和俯视图正确.左视图中间有一条横线,故左视图不正确.
故选:B.
7.解:从正面看,选项A中的图形比较符合题意,
故选:A.
8.解:A、这个几何体是圆锥,故本选项不符合题意;
B、这个几何体是圆台,故本选项不符合题意;
C、这个几何体是圆柱,故本选项符合题意;
D、这个几何体是棱台,故本选项不符合题意.
故选:C.
9.解:由图可得:
第(1)个图形中正方体的个数为1;
第(2)个图形中正方体的个数为4=1+3;
第(3)个图形中正方体的个数为10=1+3+6;
第(4)个图形中正方体的个数为20=1+3+6+10;
故第n个图形中的正方体的个数为1+3+6+…+,
∴第(5)个图形中正方体的个数为1+3+6+10+15=35;
第(6)个图形中正方体的个数为1+3+6+10+15+21=56;
故选:C.
10.解:A、流星划过夜空,属于点动成线,本选项符合题意.
B、打开折扇,属于线动成面,本选项不符合题意.
C、汽车雨刷的转动,属于线动成面,本选项不符合题意.
D、旋转门的旋转,属于面动成体,本选项不符合题意,
故选:A.
二.填空题
11.解:主视图为三个左右相邻的矩形;左视图为两个左右相邻的长方形;俯视图为六边形;所以该图为所给几何体的主视图.
12.解:从上面看三个正方形组成的矩形,
矩形的面积为1×3=3.
故答案为:3.
13.解:由n棱柱有3n条棱,
所以一个棱柱有18条棱,则它是18÷3=6,因此它是六棱柱,
而六棱柱有6+2=8个面,
故答案为:八.
14.解:一个三棱柱,有6个顶点,9条棱.
故答案为:6,9.
15.解:一个棱柱共有15条棱,那么它是五棱柱,有7个面,
故答案为:五;7.
16.解:∵一桶油漆可刷的面积为1500dm2,小明用这桶油漆恰好刷完10个同样的正方体形状的盒子的全部外表面,
∴每个正方体形状的盒子的表面积为:1500÷10=150dm2,
根据正方体表面积公式:6a2=150,
解得:a=5dm.
故答案为:5.
17.解:按照图中的位置摆放,正六边形是俯视图,三个矩形是主视图,两个矩形是左视图.故依次主视图,俯视图和左视图.
18.解:①正方体的三视图都是大小相同的正方形;
②球的三视图是大小相同的圆,
③圆锥、④圆柱、⑤三棱柱的三视图都不完全相同.
所以主视图、左视图、俯视图都完全相同的是①②.
故答案为:①②.
19.解:直角三角形绕它的直角边边旋转一周可形成圆锥.
故答案为圆锥.
20.解:(1)根据如图所示即可数出有11块小正方体;
(2)如图所示;左视图,俯视图分别如下图:
故答案为:(1)11.
三.解答题
21.解:设倒完以后,第一个容器中的水面离容器口有x cm,
则:π×42×(20﹣x)=π×62×8,
解得:x=2,
答:第一个容器中的水面离容器口有2 cm.
22.解:(1)(1×3+2×3+1×2)×2=22(m2),
(2)根据棱柱的展开与折叠,可以折叠成长方体的盒子,如图所示,其长、宽、高分别为3m,2m,1m,
因此体积为:1×2×3=6(m3),
23.解:(1)(7.9+7.8+8+7.9+8+8+7.9+7.9+7.8+7.8)÷10=7.9(cm);
(2)长=(7.9+0.2)×5+6+0.5=47(cm),
宽=(7.9+0.2)×4+5+0.5=38(cm),
高=(7.9+0.2)÷2+1+5≈10(cm);
(3)箱身=47×38+47×10×2+38×10×2=3486(cm)2,
较合理的一种方案:面积为3486cm2.
24.解:如图所示:
25.解:(1)四棱柱有6个面,12条棱,8个顶点;
(2)六棱柱有8个面,18条棱,12个顶点;
(3)由此猜想n棱柱有(n+2)个面,3n条棱,2n个顶点.
故答案为:(1)6,12,8;(2)8,18,12;(3)(n+2),3n,2n.
26.解:从第一行的平面图形绕某一边旋转可得到第二行的立体图形,从第二行的立体图形的上面看可得到第三行的平面图形.
(1)→(三)→(D);
(2)→(二)→(C);
(3)→(四)→(B);
(4)→(一)→(A).
27.解:(1)主视图有2列,每列小正方形数目分别为2,3;左视图有2列,每列小正方形数目分别为3,1,
图形分别如下:
(2)由题意可得:上面共有3个小正方形,下面共有3个小正方形;左面共有4个小正方形,右面共有4个正方形;前面共有5个小正方形,后面共有5个正方形,
故可得表面积为:1×(3+3+4+4+5+5)=24.
(3)要使表面积最大,则需满足两正方体重合的最少,此时俯视图为:
这样上面共有3个小正方形,下面共有3个小正方形;左面共有5个小正方形,右面共有5个正方形;前面共有5个小正方形,后面共有5个正方形,
表面积为:1×(3+3+5+5+5+5)=26.
故答案为:24、26.
一.选择题
1.下列几何体没有曲面的是( )
A.圆柱 B.圆锥 C.球 D.长方体
2.一个六棱柱模型如图所示,底面边长都是5cm,侧棱长为4cm,这个六棱柱的所有侧面的面积之和是( )
A.20cm2 B.60cm2 C.120cm2 D.240cm2
3.下列几何体中,正视图、左视图和俯视图完全相同的是( )
A.圆锥 B.长方体
C.圆柱 D.正方体
4.如图是一个圆柱体,则它的主视图是( )
A. B. C. D.
5.如图立体图形中,三视图都一样的是( )
A. B. C. D.
6.某同学画出了如图所示的几何体的三种视图,其中正确的是( )
A.①② B.①③ C.②③ D.②
7.如图,这是一个由2个大小不一样的圆柱组成的几何体,则该几何体的主视图是( )
A. B. C. D.
8.下列几何体中,圆柱体是( )
A. B. C. D.
9.如图,都是由边长为1的正方体叠成的立体图形,例如第(1)个图形由1个正方体叠成,第(2)个图形由4个正方体叠成,第(3)个图形由10个正方体叠成,依次规律,第(6)个图形由( )个正方体叠成.
A.36 B.37 C.56 D.84
10.几何图形都是由点、线、面、体组成的,点动成线,线动成面,面动成体,下列生活现象中可以反映“点动成线”的是( )
A.流星划过夜空 B.打开折扇
C.汽车雨刷的转动 D.旋转门的旋转
二.填空题
11.如图中物体的一个视图(a)的名称为 .
12.如图,由四个小正方体组成的几何体中,若每个小正方体的棱长都是1,则该几何体俯视图的面积是 .
13.一个棱柱有18条棱,则这个棱柱共有 个面.
14.一个三棱柱有 个顶点, 条棱.
15.一个棱柱共有15条棱,那么它是 棱柱,有 个面.
16.一桶油漆可刷的面积为1500dm2,小明用这桶油漆恰好刷完10个同样的正方体形状的盒子的全部外表面,则此正方体盒子的棱长是 dm.
17.请将六棱柱的三视图名称依次填在横线上 .
18.在①正方体、②球、③圆锥、④圆柱、⑤三棱柱这五种几何体中,其主视图、左视图、俯视图都完全相同的是 .
19.把三角板绕着一条直角边旋转一圈,则所围成的几何体是 .
20.如图,是由一些大小相同的小正方体组合成的简单几何体
(1)图中有 块小正方体;
(2)该几何体的主视图如图所示,请在下面方格纸中分别画出它的左视图和俯视图.
三.解答题
21.两个圆柱体容器如图所示,容器1的半径是4cm,高是20cm;容器2的半径是6cm,高是8cm,我们先在容器2中倒满水,然后将里面的水全部倒入容器1中,问:倒完以后,容器1中的水面离容器口有多少厘米?
22.如图所示是一张铁皮.
(1)计算该铁皮的面积;
(2)它能否做成一个长方体盒子?若能,画出来,计算它的体积;若不能,说明理由.
23.台州奉化一果农有一批经过挑选的橙子要包装出售,现随意挑选10个,橙子测量直径,数据分别为(单位:cm)7.9,7.8,8,7.9,8,8,7.9,7.9,7.8,7.8.橙子内包装模型的横截面如图(1),凹型为半圆形,半圆的直径为这批橙子大约平均值加0.2cm,现用纸箱作外包装,内包装嵌入纸箱内,每箱装一层,一层装5×4个如图(2)所示,纸箱的高度比内包装高5cm.
(1)估计这批橙子的平均直径大约是多少?
(2)设计纸箱(不加盖子)的长、宽、高各为多少?(数据保留整数,设计时长和宽比内包装各需加长0.5cm).
(3)加工成一只纸箱的硬纸板面积较合理需多少cm2,请给出一种方案.(不计接头重叠部分,盖子顶面用透明纸)
24.如图是由7个完全相同的小立方块搭成的几何体,请画出它的三视图.
25.如图四个几何体分别是三棱柱,四棱柱,五棱柱和六棱柱,三棱柱有5个面,9条棱,6个顶点,观察图形,填写下面的空.
(1)四棱柱有 个面, 条棱, 个顶点;
(2)六棱柱有 个面, 条棱, 个顶点;
(3)由此猜想n棱柱有 个面, 条棱, 个顶点.
26.用数学的眼光去观察问题,你会发现很多图形都能看成是动静结合,舒展自如的.下面所给的三排图形都存在着某种联系,用线将它们连起来.
27.由几个相同的边长为1的小立方块搭成的几何体的俯视图如下图,格中的数字表示该位置的小立方块的个数.
(1)请在下面方格纸中分别画出这个向何体的主视图和左视图.
(2)根据三视图;这个组合几何体的表面积为 个平方单位.(包括底面积)
(3)若上述小立方块搭成的几何体的俯视图不变,各位置的小立方块个数可以改变(总数目不变),则搭成这样的组合几何体中的表面积最大是为 个平方单位.(包括底面积)
参考答案与试题解析
一.选择题
1.解:A、圆柱由2个平面和一个曲面组成,不符合题意;
B、圆锥由一个平面和一个曲面组成,不符合题意;
C、球由一个曲面组成,不符合题意;
D、长方体是由六个平面组成,符合题意.
故选:D.
2.解:六棱柱的侧面积为:4×5×6=120(cm2).
故选:C.
3.解:A、圆锥的正视图为三角形,左视图为三角形,俯视图为含有直径的圆,故本选项错误;
B、长方体的正视图为矩形,左视图为矩形,俯视图为矩形,但三个矩形的形状不一样,故本选项错误;
C、圆柱的正视图为矩形,左视图为距形,俯视图为圆,故本选项错误;
D、正方形的正视图为正方形,主视图为正方形,俯视图为正方形,故本选项正确;
故选:D.
4.解:一个直立在水平面上的圆柱体的主视图是长方形,
故选:A.
5.解:A、圆柱的主视图和左视图是矩形,俯视图是圆,故本选项不合题意;
B、圆锥的主视图和左视图是三角形,俯视图是带有圆心的圆,故本选项不合题意;
C、立方体的三视图都是正方形,故本选项符合题意;
D、三棱柱的主视图和俯视图是矩形,左视图是三角形,故本选项不合题意.
故选:C.
6.解:根据几何体的摆放位置,主视图和俯视图正确.左视图中间有一条横线,故左视图不正确.
故选:B.
7.解:从正面看,选项A中的图形比较符合题意,
故选:A.
8.解:A、这个几何体是圆锥,故本选项不符合题意;
B、这个几何体是圆台,故本选项不符合题意;
C、这个几何体是圆柱,故本选项符合题意;
D、这个几何体是棱台,故本选项不符合题意.
故选:C.
9.解:由图可得:
第(1)个图形中正方体的个数为1;
第(2)个图形中正方体的个数为4=1+3;
第(3)个图形中正方体的个数为10=1+3+6;
第(4)个图形中正方体的个数为20=1+3+6+10;
故第n个图形中的正方体的个数为1+3+6+…+,
∴第(5)个图形中正方体的个数为1+3+6+10+15=35;
第(6)个图形中正方体的个数为1+3+6+10+15+21=56;
故选:C.
10.解:A、流星划过夜空,属于点动成线,本选项符合题意.
B、打开折扇,属于线动成面,本选项不符合题意.
C、汽车雨刷的转动,属于线动成面,本选项不符合题意.
D、旋转门的旋转,属于面动成体,本选项不符合题意,
故选:A.
二.填空题
11.解:主视图为三个左右相邻的矩形;左视图为两个左右相邻的长方形;俯视图为六边形;所以该图为所给几何体的主视图.
12.解:从上面看三个正方形组成的矩形,
矩形的面积为1×3=3.
故答案为:3.
13.解:由n棱柱有3n条棱,
所以一个棱柱有18条棱,则它是18÷3=6,因此它是六棱柱,
而六棱柱有6+2=8个面,
故答案为:八.
14.解:一个三棱柱,有6个顶点,9条棱.
故答案为:6,9.
15.解:一个棱柱共有15条棱,那么它是五棱柱,有7个面,
故答案为:五;7.
16.解:∵一桶油漆可刷的面积为1500dm2,小明用这桶油漆恰好刷完10个同样的正方体形状的盒子的全部外表面,
∴每个正方体形状的盒子的表面积为:1500÷10=150dm2,
根据正方体表面积公式:6a2=150,
解得:a=5dm.
故答案为:5.
17.解:按照图中的位置摆放,正六边形是俯视图,三个矩形是主视图,两个矩形是左视图.故依次主视图,俯视图和左视图.
18.解:①正方体的三视图都是大小相同的正方形;
②球的三视图是大小相同的圆,
③圆锥、④圆柱、⑤三棱柱的三视图都不完全相同.
所以主视图、左视图、俯视图都完全相同的是①②.
故答案为:①②.
19.解:直角三角形绕它的直角边边旋转一周可形成圆锥.
故答案为圆锥.
20.解:(1)根据如图所示即可数出有11块小正方体;
(2)如图所示;左视图,俯视图分别如下图:
故答案为:(1)11.
三.解答题
21.解:设倒完以后,第一个容器中的水面离容器口有x cm,
则:π×42×(20﹣x)=π×62×8,
解得:x=2,
答:第一个容器中的水面离容器口有2 cm.
22.解:(1)(1×3+2×3+1×2)×2=22(m2),
(2)根据棱柱的展开与折叠,可以折叠成长方体的盒子,如图所示,其长、宽、高分别为3m,2m,1m,
因此体积为:1×2×3=6(m3),
23.解:(1)(7.9+7.8+8+7.9+8+8+7.9+7.9+7.8+7.8)÷10=7.9(cm);
(2)长=(7.9+0.2)×5+6+0.5=47(cm),
宽=(7.9+0.2)×4+5+0.5=38(cm),
高=(7.9+0.2)÷2+1+5≈10(cm);
(3)箱身=47×38+47×10×2+38×10×2=3486(cm)2,
较合理的一种方案:面积为3486cm2.
24.解:如图所示:
25.解:(1)四棱柱有6个面,12条棱,8个顶点;
(2)六棱柱有8个面,18条棱,12个顶点;
(3)由此猜想n棱柱有(n+2)个面,3n条棱,2n个顶点.
故答案为:(1)6,12,8;(2)8,18,12;(3)(n+2),3n,2n.
26.解:从第一行的平面图形绕某一边旋转可得到第二行的立体图形,从第二行的立体图形的上面看可得到第三行的平面图形.
(1)→(三)→(D);
(2)→(二)→(C);
(3)→(四)→(B);
(4)→(一)→(A).
27.解:(1)主视图有2列,每列小正方形数目分别为2,3;左视图有2列,每列小正方形数目分别为3,1,
图形分别如下:
(2)由题意可得:上面共有3个小正方形,下面共有3个小正方形;左面共有4个小正方形,右面共有4个正方形;前面共有5个小正方形,后面共有5个正方形,
故可得表面积为:1×(3+3+4+4+5+5)=24.
(3)要使表面积最大,则需满足两正方体重合的最少,此时俯视图为:
这样上面共有3个小正方形,下面共有3个小正方形;左面共有5个小正方形,右面共有5个正方形;前面共有5个小正方形,后面共有5个正方形,
表面积为:1×(3+3+5+5+5+5)=26.
故答案为:24、26.
同课章节目录
- 第1章 走进数学世界
- 数学伴我们成长
- 人类离不开数学
- 人人都能学会数学
- 第2章 有理数
- 2.1 有理数
- 2.2 数轴
- 2.3 相反数
- 2.4 绝对值
- 2.5 有理数的大小比较
- 2.6 有理数的加法
- 2.7 有理数的减法
- 2.8 有理数加减混合运算
- 2.9 有理数的乘法
- 2.10 有理数的除法
- 2.11 有理数的乘方
- 2.12 科学记数法
- 2.13 有理数的混合运算
- 2.14 近似数
- 2.15 用计算器进行计算
- 第3章 整式的加减
- 3.1 列代数式
- 3.2 代数式的值
- 3.3 整式
- 3.4 整式的加减
- 第4章 图形的初步认识
- 4.1 生活中的立体图形
- 4.2 立体图形的视图
- 4.3 立体图形的表面展开图
- 4.4 平面图形
- 4.5 最基本的图形——点和线
- 4.6 角
- 第5章 相交线与平行线
- 5.1 相交线
- 5.2 平行线
