12.3角的平分线的性质2021-2022学年度人教版八年级数学上册期中专题复习(Word版含解析)
文档属性
| 名称 | 12.3角的平分线的性质2021-2022学年度人教版八年级数学上册期中专题复习(Word版含解析) |  | |
| 格式 | docx | ||
| 文件大小 | 612.4KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
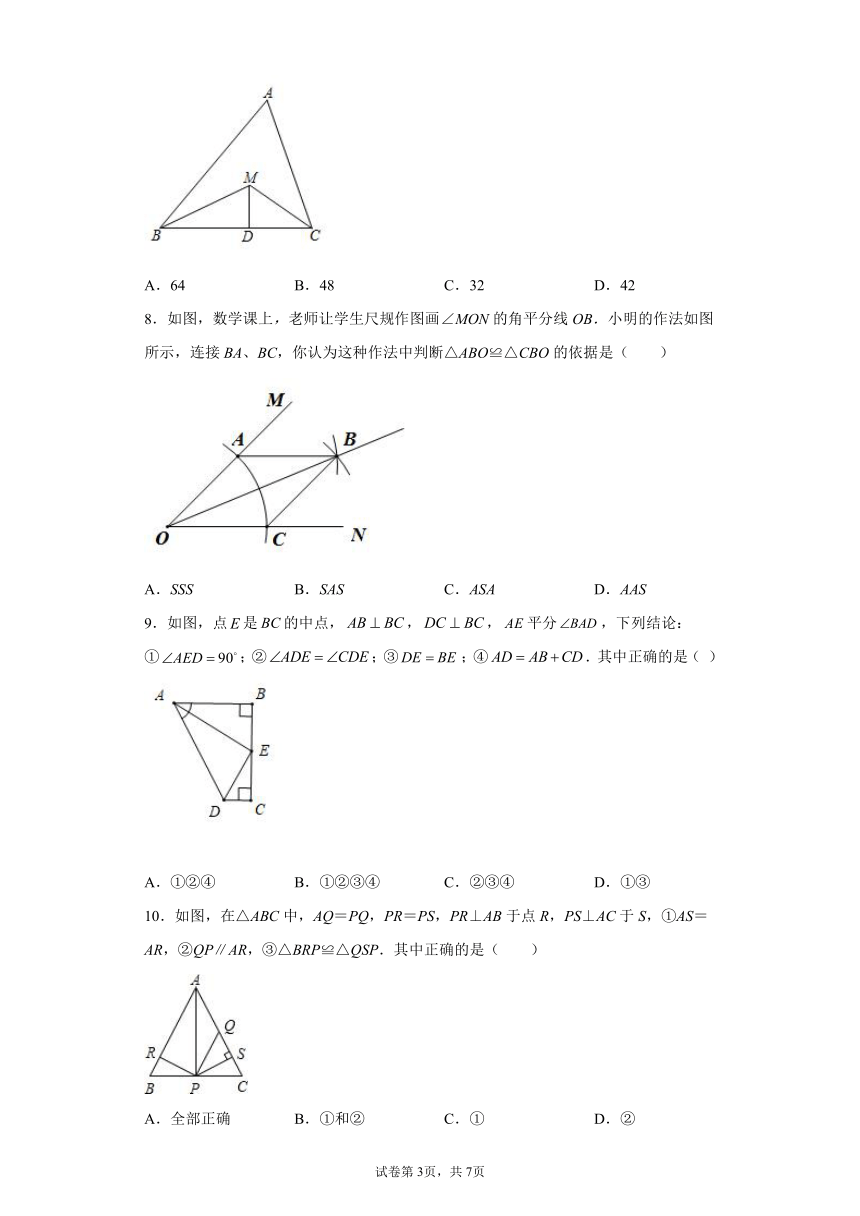
| 科目 | 数学 | ||
| 更新时间 | 2021-10-20 15:25:22 | ||
图片预览


文档简介
12.3角的平分线的性质2021-2022学年度人教版八年级数学上册期中专题复习
一、选择题
1.如图,OD平分∠AOB,DE⊥AO于点E,DE=4.2,F是射线OB上的任一点,则DF的长度不可能是( )
A.3.9 B.4.2 C.4.7 D.5.84
2.如图,点O在内,且到三边的距离相等,∠A=64°,则∠BOC的度数为( )
A.58° B.64° C.122° D.124°
3.如图,在Rt△ACB中,∠C=90°,AD平分∠BAC,若BC=15,BD=10,则点D到AB的距离是( )
A.15 B.10 C.8 D.5
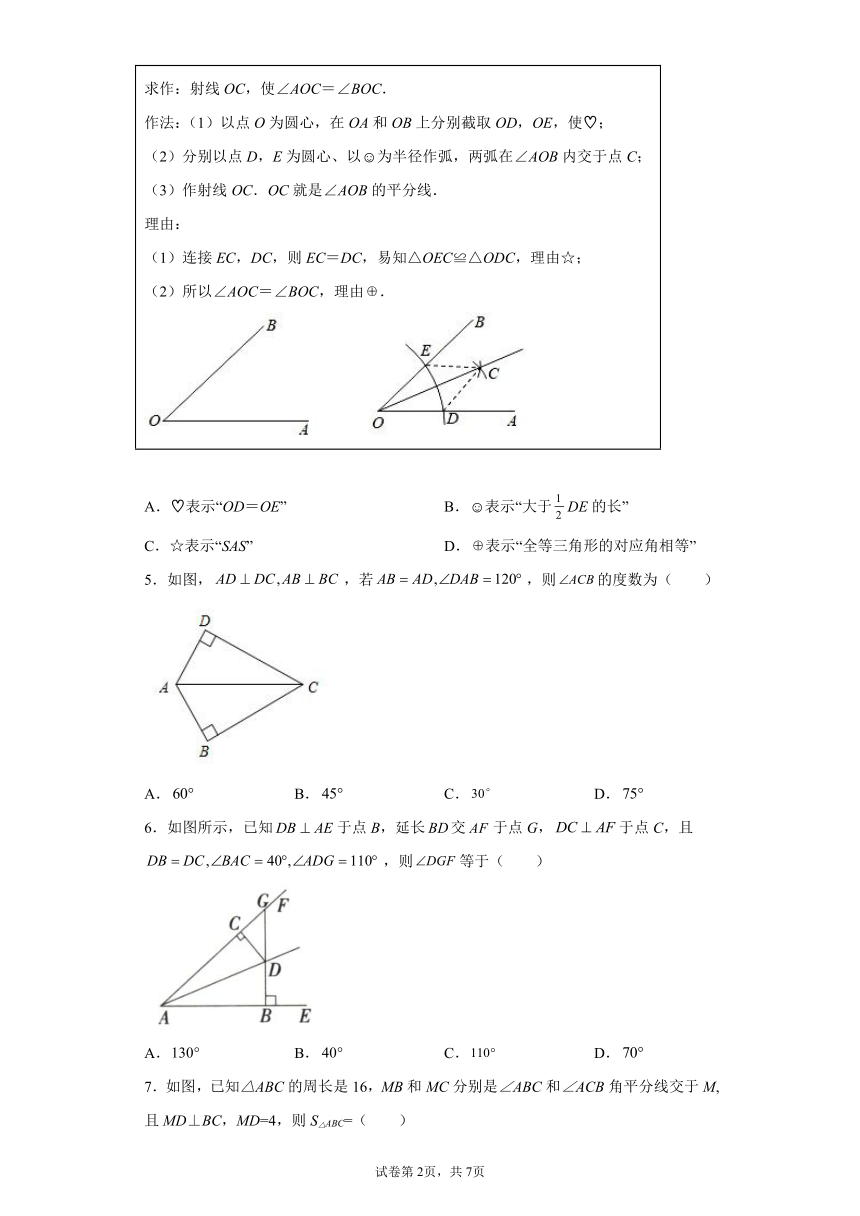
4.数学课上,小明用尺规在黑板上作∠AOB的平分线,并进行简单的说理,下面是小明的解答过程,则符号“ 、 、☆、 ”代表的内容错误的是( )
已知:∠AOB. 求作:射线OC,使∠AOC=∠BOC. 作法:(1)以点O为圆心,在OA和OB上分别截取OD,OE,使 ; (2)分别以点D,E为圆心、以 为半径作弧,两弧在∠AOB内交于点C; (3)作射线OC.OC就是∠AOB的平分线. 理由: (1)连接EC,DC,则EC=DC,易知△OEC≌△ODC,理由☆; (2)所以∠AOC=∠BOC,理由 .
A. 表示“OD=OE” B. 表示“大于DE的长”
C.☆表示“SAS” D. 表示“全等三角形的对应角相等”
5.如图,,若,则的度数为( )
A. B. C. D.
6.如图所示,已知于点B,延长交于点G,于点C,且,则等于( )
A. B. C. D.
7.如图,已知△ABC的周长是16,MB和MC分别是∠ABC和∠ACB角平分线交于M,且MD⊥BC,MD=4,则S△ABC=( )
A.64 B.48 C.32 D.42
8.如图,数学课上,老师让学生尺规作图画∠MON的角平分线OB.小明的作法如图所示,连接BA、BC,你认为这种作法中判断△ABO≌△CBO的依据是( )
A.SSS B.SAS C.ASA D.AAS
9.如图,点是的中点,,,平分,下列结论:①;②;③;④.其中正确的是( )
A.①②④ B.①②③④ C.②③④ D.①③
10.如图,在△ABC中,AQ=PQ,PR=PS,PR⊥AB于点R,PS⊥AC于S,①AS=AR,②QP∥AR,③△BRP≌△QSP.其中正确的是( )
A.全部正确 B.①和② C.① D.②
二、填空题
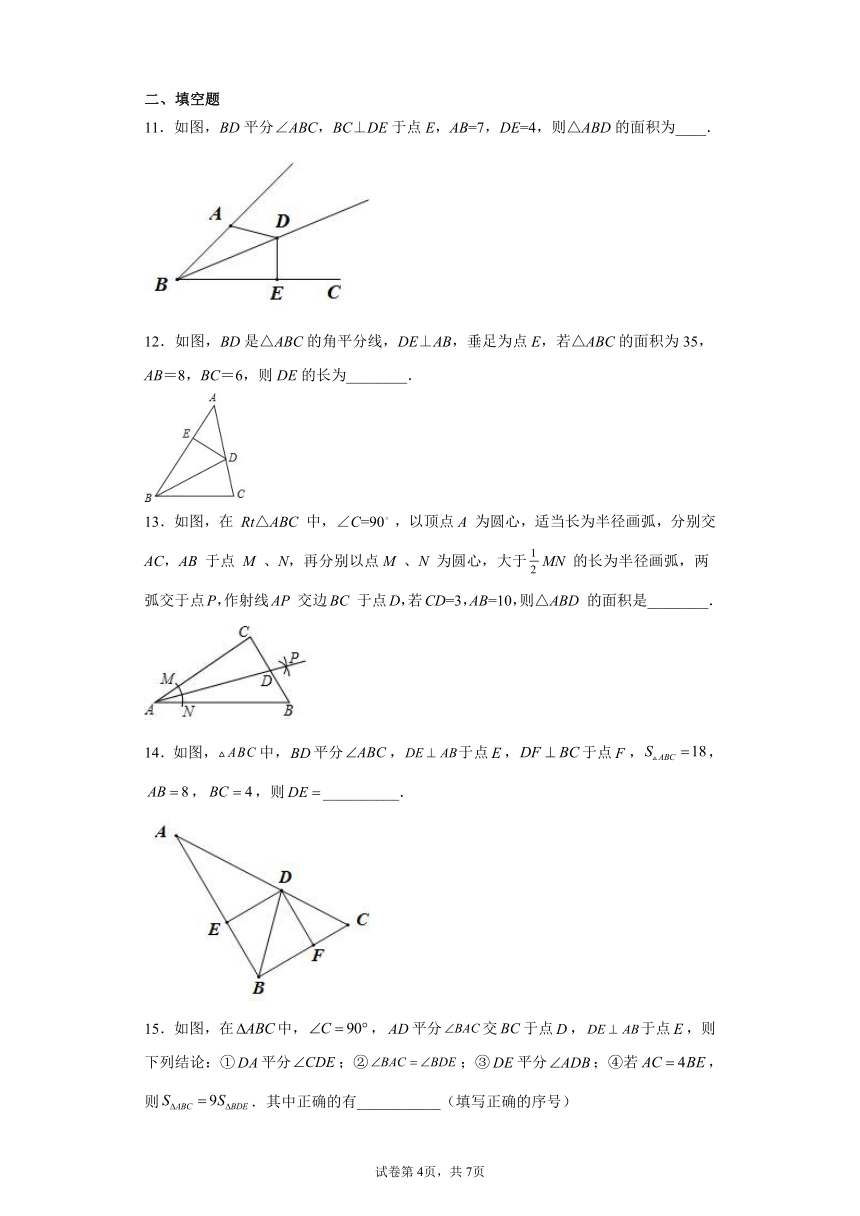
11.如图,BD平分∠ABC,BC⊥DE于点E,AB=7,DE=4,则△ABD的面积为____.
12.如图,BD是△ABC的角平分线,DE⊥AB,垂足为点E,若△ABC的面积为35,AB=8,BC=6,则DE的长为________.
13.如图,在 Rt△ABC 中,∠C=90 ,以顶点A 为圆心,适当长为半径画弧,分别交AC,AB 于点 M 、N,再分别以点M 、N 为圆心,大于MN 的长为半径画弧,两弧交于点P,作射线AP 交边BC 于点D,若CD=3,AB=10,则△ABD 的面积是________.
14.如图,中,平分,于点,于点,,,,则__________.
15.如图,在中,,平分交于点,于点,则下列结论:①平分;②;③平分;④若,则.其中正确的有___________(填写正确的序号)
16.如图,在△ABC中,AB=5,AC=8,BC=9,以A为圆心,以适当的长为半径作弧,交AB于点M,交AC于点N.分别以M,N为圆心,以大于MN的长为半径作弧,两弧在∠BAC的内部相交于点G,作射线AG,交BC于点D,点F在AC边上,AF=AB,连接DF,则△CDF的周长为_____.
三、解答题
17.已知,如图,AB=AC,BD=CD,DE⊥AB于点E,DF⊥AC于点F,试问:DE和DF相等吗?说明理由.
18.如图,在中,AD是角平分线,E,F分别为AC,AB上的点,且.
(1)求证:;
(2)DE与DF有何数量关系?请说明理由.(可根据答卷图中的提示解答)
19.如图,DE⊥AB于E,DF⊥AC于F,若BD =CD、BE=CF.
(1)求证:AD平分∠BAC;
(2)已知AB=5,AC=8,求BE的长.
20.如图1,在中,是的平分线,P是上一点,交于点E,交于点F.
(1)求证:D到的距离与D到的距离相等;
(2)如图2,若点P在的延长线上,其他条件不变,试猜想(1)中的结论还成立吗?请证明你的猜想.
21.如图①,在中,是的中点,,,垂足分别为,,.
(1)证明:是的角平分线.
(2)如图②,若,,,点为线段上一个动点,过点分别作,的垂线段,垂足分别为、,则是定值吗?若是,求出该定值;若不是,请说明理由.
22.已知中,平分,交于,在上,点在延长线上,连接、,交于点,交于点,.
(1)求证:;
(2)点为上一点,连接,,,求证:平分;
(3)在(2)的条件下,,,求的度数.
试卷第1页,共3页
试卷第1页,共3页
参考答案
1.A
解:过D点作DH⊥OB于H,如图,
∵OD平分∠AOB,DE⊥AO,DH⊥OB,
∴DH=DE=4.2,
∵F是射线OB上的任一点,
∴DF≥4.2.
故选:A.
2.C
解:点在内,且到三边的距离相等,
即点到和的距离相等,点到和的距离相等,
平分,平分,
,,
,
,
,
.
故选:C.
3.D
解:过D点作DE⊥AB于E,如图,
∵BC=15,BD=10,
∴CD=BC-BD=5,
∵AD平分∠BAC,DC⊥AC,DE⊥AB,
∴DE=DC=5,
∴点D到AB的距离为5.
故选:D.
4.C
解:作法:(1)以点O为圆心,在OA和OB上分别截取OD,OE,使OE=OD,
(2)分别以点D,E为圆心、以大于 DE为半径作弧,两弧在∠AOB内交于点C;
(3)作射线OC.OC就是∠AOB的平分线.
理由:(1)连接EC,DC,则EC=DC,易知△OEC≌△ODC,理由SSS;
(2)所以∠AOC=∠BOC,理由全等三角形的对应角相等.
故选C.
5.C
∵,
∴平分,
∵,
∴,
∴,
故选:C.
6.A
∵于点B,于点C,且,
∴平分,
∵,
∴,
∵,
∴,
故选:A.
7.C
解:如图所示,连接AM,过点M分别作ME⊥AB于E,MF⊥AC于F,
∵MB平分∠ABC,MC平分∠ACB,
∴ME=MD=MF,
∵,
∴,
∵△ABC的周长是16,
∴AB+BC+AC=16,
∴=32,
故选C.
8.A
作法:①以O为圆心,任意长为半径画弧,交MO、NO于点A、G,
②再分别以A、G为圆心,大于AG长为半径画弧,两弧交于点B,
③画射线OB,射线OB即为所求,
由作图过程可得:OA=OG,AB=GB,而OB=OB,
则用到的三角形全等的判定方法是:SSS.
故选:A.
9.A
解:过E作EF⊥AD于F,如图,
∵AB⊥BC,AE平分∠BAD,
∴BE=EF,AE=AE,
∴Rt△AEF≌Rt△AEB(HL)
∴AB=AF,∠AEF=∠AEB;
而点E是BC的中点,
∴EC=EF=BE,所以③错误;
∵EC=EF,ED=ED,
∴Rt△EFD≌Rt△ECD(HL),
∴DC=DF,∠FDE=∠CDE,所以②正确;
∴AD=AF+FD=AB+DC,所以④正确;
∴∠AED=∠AEF+∠FED=∠BEC=90°,所以①正确,
综上:①②④正确,
故选A
10.B
解:①∵PR⊥AB,PS⊥AC,垂足分别为R、S,PR=PS.
∴AP为∠BAC的角平分线,
在△APR与△APS中,
,
∴△APR≌△APS(HL),
∴AR=AS,故本小题正确;
②∵AP为∠BAC的角平分线,
∴∠RAP=∠QAP,
∵AQ=PQ,
∴∠QAP=∠QPA,
∴∠RAP=∠QPA,
∴QP∥AR,故本小题正确;
③△BRP与△QSP只有一组边PR=PS,一组角∠PSQ=∠PRB=90°,
全等的条件不够,没法证明其全等,故本小题错误.
综上所述,①②正确.
故选:B.
11.14
解:过点D作DF⊥AB于点F,如图所示:
∵BD平分∠ABC,BC⊥DE,DE=4,
∴DF=DE=4,
∵AB=7,
∴;
故答案为14.
12.5
作DF⊥BC于F,
∵BD是△ABC的角平分线,DE⊥AB,DF⊥BC,
∴DF=DE,
∴S△ABC=S△ABD+S△DBC=×AB×DE+×BC×DF=×(AB+BC) DE=×(8+6) DE=35,∴DE=5.
故答案为:5.
13.15
如图,过点D作DH⊥AB于H.
∵AP平分∠CAB,DC⊥AC,DH⊥AB,
∴DC=DH=3,
∴S△ABD=AB×DH=×10×3=15,
故答案为:15.
14.3
解:∵BD是∠ABC的平分线,DE⊥AB于点E,DF⊥BC于点F,
∴DE=DF,
∵S△ABC=S△ABD+S△BDC=AB DE+BC DF=18,
即×8 DE+×4 DE=18,
解得:DE=3,
故答案为:3.
15.①②④
解:平分,
,
,,
,
,
,
,
①平分正确;
无法证明,
③平分错误;
,,
,
,,
,,
,
④正确;
,,
,
②正确.
故答案是:①②④.
16.12
解:,,,
,
由作图方法可得:平分,
,
在和中
,
,
,
的周长为:.
故答案为:12.
17
连接AD,如图,
在△ACD和△ABD中,
,
∴ACD≌△ABD(SSS),
即
∵DE⊥AE,DF⊥AF,
∴DE=DF.
18.
(1),
(2),
理由如下:
过点D分别作于点M,于点N,如图,
,
是角平分线,
,
,
19.
(1)证明:∵,
∴,
又∵
∴
∴
又∵,
∴点在的角平分线上
∴平分
(2)解:∵
∴
又∵,,
∴
∴
∴
又∵
∴
∴
20.
解:(1)证明:∵,
∴,
在中,是的平分线,
∴,
∴,即平分,
∴D到的距离与D到的距离相等;
(2)若点P在的延长线上,其他条件不变,(1)中的结论还成立.
证明:∵,
∴,
∵在中,是的平分线,
∴,
∴,即平分,
∴D到的距离与D到的距离相等.
21.
证明:(1)∵为的中点,
∴.
又∵,,
∴
∴在与中,
,
∴,
∴,
又∵,,
∴是的角平分线;
(2)如图②,连接,
∵,
∴,
∴,
∴.
22.
解:(1)证明:,,
,
,
,
又平分,
∴∠EBD=∠CBD,
.
(2),
,
由(1)知,
,
又,
,
又,
,
平分.
(3),平分,
,
又,
,
,
又,
,
由(2)知,平分,
.
答案第1页,共2页
答案第1页,共2页
一、选择题
1.如图,OD平分∠AOB,DE⊥AO于点E,DE=4.2,F是射线OB上的任一点,则DF的长度不可能是( )
A.3.9 B.4.2 C.4.7 D.5.84
2.如图,点O在内,且到三边的距离相等,∠A=64°,则∠BOC的度数为( )
A.58° B.64° C.122° D.124°
3.如图,在Rt△ACB中,∠C=90°,AD平分∠BAC,若BC=15,BD=10,则点D到AB的距离是( )
A.15 B.10 C.8 D.5
4.数学课上,小明用尺规在黑板上作∠AOB的平分线,并进行简单的说理,下面是小明的解答过程,则符号“ 、 、☆、 ”代表的内容错误的是( )
已知:∠AOB. 求作:射线OC,使∠AOC=∠BOC. 作法:(1)以点O为圆心,在OA和OB上分别截取OD,OE,使 ; (2)分别以点D,E为圆心、以 为半径作弧,两弧在∠AOB内交于点C; (3)作射线OC.OC就是∠AOB的平分线. 理由: (1)连接EC,DC,则EC=DC,易知△OEC≌△ODC,理由☆; (2)所以∠AOC=∠BOC,理由 .
A. 表示“OD=OE” B. 表示“大于DE的长”
C.☆表示“SAS” D. 表示“全等三角形的对应角相等”
5.如图,,若,则的度数为( )
A. B. C. D.
6.如图所示,已知于点B,延长交于点G,于点C,且,则等于( )
A. B. C. D.
7.如图,已知△ABC的周长是16,MB和MC分别是∠ABC和∠ACB角平分线交于M,且MD⊥BC,MD=4,则S△ABC=( )
A.64 B.48 C.32 D.42
8.如图,数学课上,老师让学生尺规作图画∠MON的角平分线OB.小明的作法如图所示,连接BA、BC,你认为这种作法中判断△ABO≌△CBO的依据是( )
A.SSS B.SAS C.ASA D.AAS
9.如图,点是的中点,,,平分,下列结论:①;②;③;④.其中正确的是( )
A.①②④ B.①②③④ C.②③④ D.①③
10.如图,在△ABC中,AQ=PQ,PR=PS,PR⊥AB于点R,PS⊥AC于S,①AS=AR,②QP∥AR,③△BRP≌△QSP.其中正确的是( )
A.全部正确 B.①和② C.① D.②
二、填空题
11.如图,BD平分∠ABC,BC⊥DE于点E,AB=7,DE=4,则△ABD的面积为____.
12.如图,BD是△ABC的角平分线,DE⊥AB,垂足为点E,若△ABC的面积为35,AB=8,BC=6,则DE的长为________.
13.如图,在 Rt△ABC 中,∠C=90 ,以顶点A 为圆心,适当长为半径画弧,分别交AC,AB 于点 M 、N,再分别以点M 、N 为圆心,大于MN 的长为半径画弧,两弧交于点P,作射线AP 交边BC 于点D,若CD=3,AB=10,则△ABD 的面积是________.
14.如图,中,平分,于点,于点,,,,则__________.
15.如图,在中,,平分交于点,于点,则下列结论:①平分;②;③平分;④若,则.其中正确的有___________(填写正确的序号)
16.如图,在△ABC中,AB=5,AC=8,BC=9,以A为圆心,以适当的长为半径作弧,交AB于点M,交AC于点N.分别以M,N为圆心,以大于MN的长为半径作弧,两弧在∠BAC的内部相交于点G,作射线AG,交BC于点D,点F在AC边上,AF=AB,连接DF,则△CDF的周长为_____.
三、解答题
17.已知,如图,AB=AC,BD=CD,DE⊥AB于点E,DF⊥AC于点F,试问:DE和DF相等吗?说明理由.
18.如图,在中,AD是角平分线,E,F分别为AC,AB上的点,且.
(1)求证:;
(2)DE与DF有何数量关系?请说明理由.(可根据答卷图中的提示解答)
19.如图,DE⊥AB于E,DF⊥AC于F,若BD =CD、BE=CF.
(1)求证:AD平分∠BAC;
(2)已知AB=5,AC=8,求BE的长.
20.如图1,在中,是的平分线,P是上一点,交于点E,交于点F.
(1)求证:D到的距离与D到的距离相等;
(2)如图2,若点P在的延长线上,其他条件不变,试猜想(1)中的结论还成立吗?请证明你的猜想.
21.如图①,在中,是的中点,,,垂足分别为,,.
(1)证明:是的角平分线.
(2)如图②,若,,,点为线段上一个动点,过点分别作,的垂线段,垂足分别为、,则是定值吗?若是,求出该定值;若不是,请说明理由.
22.已知中,平分,交于,在上,点在延长线上,连接、,交于点,交于点,.
(1)求证:;
(2)点为上一点,连接,,,求证:平分;
(3)在(2)的条件下,,,求的度数.
试卷第1页,共3页
试卷第1页,共3页
参考答案
1.A
解:过D点作DH⊥OB于H,如图,
∵OD平分∠AOB,DE⊥AO,DH⊥OB,
∴DH=DE=4.2,
∵F是射线OB上的任一点,
∴DF≥4.2.
故选:A.
2.C
解:点在内,且到三边的距离相等,
即点到和的距离相等,点到和的距离相等,
平分,平分,
,,
,
,
,
.
故选:C.
3.D
解:过D点作DE⊥AB于E,如图,
∵BC=15,BD=10,
∴CD=BC-BD=5,
∵AD平分∠BAC,DC⊥AC,DE⊥AB,
∴DE=DC=5,
∴点D到AB的距离为5.
故选:D.
4.C
解:作法:(1)以点O为圆心,在OA和OB上分别截取OD,OE,使OE=OD,
(2)分别以点D,E为圆心、以大于 DE为半径作弧,两弧在∠AOB内交于点C;
(3)作射线OC.OC就是∠AOB的平分线.
理由:(1)连接EC,DC,则EC=DC,易知△OEC≌△ODC,理由SSS;
(2)所以∠AOC=∠BOC,理由全等三角形的对应角相等.
故选C.
5.C
∵,
∴平分,
∵,
∴,
∴,
故选:C.
6.A
∵于点B,于点C,且,
∴平分,
∵,
∴,
∵,
∴,
故选:A.
7.C
解:如图所示,连接AM,过点M分别作ME⊥AB于E,MF⊥AC于F,
∵MB平分∠ABC,MC平分∠ACB,
∴ME=MD=MF,
∵,
∴,
∵△ABC的周长是16,
∴AB+BC+AC=16,
∴=32,
故选C.
8.A
作法:①以O为圆心,任意长为半径画弧,交MO、NO于点A、G,
②再分别以A、G为圆心,大于AG长为半径画弧,两弧交于点B,
③画射线OB,射线OB即为所求,
由作图过程可得:OA=OG,AB=GB,而OB=OB,
则用到的三角形全等的判定方法是:SSS.
故选:A.
9.A
解:过E作EF⊥AD于F,如图,
∵AB⊥BC,AE平分∠BAD,
∴BE=EF,AE=AE,
∴Rt△AEF≌Rt△AEB(HL)
∴AB=AF,∠AEF=∠AEB;
而点E是BC的中点,
∴EC=EF=BE,所以③错误;
∵EC=EF,ED=ED,
∴Rt△EFD≌Rt△ECD(HL),
∴DC=DF,∠FDE=∠CDE,所以②正确;
∴AD=AF+FD=AB+DC,所以④正确;
∴∠AED=∠AEF+∠FED=∠BEC=90°,所以①正确,
综上:①②④正确,
故选A
10.B
解:①∵PR⊥AB,PS⊥AC,垂足分别为R、S,PR=PS.
∴AP为∠BAC的角平分线,
在△APR与△APS中,
,
∴△APR≌△APS(HL),
∴AR=AS,故本小题正确;
②∵AP为∠BAC的角平分线,
∴∠RAP=∠QAP,
∵AQ=PQ,
∴∠QAP=∠QPA,
∴∠RAP=∠QPA,
∴QP∥AR,故本小题正确;
③△BRP与△QSP只有一组边PR=PS,一组角∠PSQ=∠PRB=90°,
全等的条件不够,没法证明其全等,故本小题错误.
综上所述,①②正确.
故选:B.
11.14
解:过点D作DF⊥AB于点F,如图所示:
∵BD平分∠ABC,BC⊥DE,DE=4,
∴DF=DE=4,
∵AB=7,
∴;
故答案为14.
12.5
作DF⊥BC于F,
∵BD是△ABC的角平分线,DE⊥AB,DF⊥BC,
∴DF=DE,
∴S△ABC=S△ABD+S△DBC=×AB×DE+×BC×DF=×(AB+BC) DE=×(8+6) DE=35,∴DE=5.
故答案为:5.
13.15
如图,过点D作DH⊥AB于H.
∵AP平分∠CAB,DC⊥AC,DH⊥AB,
∴DC=DH=3,
∴S△ABD=AB×DH=×10×3=15,
故答案为:15.
14.3
解:∵BD是∠ABC的平分线,DE⊥AB于点E,DF⊥BC于点F,
∴DE=DF,
∵S△ABC=S△ABD+S△BDC=AB DE+BC DF=18,
即×8 DE+×4 DE=18,
解得:DE=3,
故答案为:3.
15.①②④
解:平分,
,
,,
,
,
,
,
①平分正确;
无法证明,
③平分错误;
,,
,
,,
,,
,
④正确;
,,
,
②正确.
故答案是:①②④.
16.12
解:,,,
,
由作图方法可得:平分,
,
在和中
,
,
,
的周长为:.
故答案为:12.
17
连接AD,如图,
在△ACD和△ABD中,
,
∴ACD≌△ABD(SSS),
即
∵DE⊥AE,DF⊥AF,
∴DE=DF.
18.
(1),
(2),
理由如下:
过点D分别作于点M,于点N,如图,
,
是角平分线,
,
,
19.
(1)证明:∵,
∴,
又∵
∴
∴
又∵,
∴点在的角平分线上
∴平分
(2)解:∵
∴
又∵,,
∴
∴
∴
又∵
∴
∴
20.
解:(1)证明:∵,
∴,
在中,是的平分线,
∴,
∴,即平分,
∴D到的距离与D到的距离相等;
(2)若点P在的延长线上,其他条件不变,(1)中的结论还成立.
证明:∵,
∴,
∵在中,是的平分线,
∴,
∴,即平分,
∴D到的距离与D到的距离相等.
21.
证明:(1)∵为的中点,
∴.
又∵,,
∴
∴在与中,
,
∴,
∴,
又∵,,
∴是的角平分线;
(2)如图②,连接,
∵,
∴,
∴,
∴.
22.
解:(1)证明:,,
,
,
,
又平分,
∴∠EBD=∠CBD,
.
(2),
,
由(1)知,
,
又,
,
又,
,
平分.
(3),平分,
,
又,
,
,
又,
,
由(2)知,平分,
.
答案第1页,共2页
答案第1页,共2页
