13.1轴对称2021-2022学年度人教版八年级数学上册期中专题复习(Word版含解析)
文档属性
| 名称 | 13.1轴对称2021-2022学年度人教版八年级数学上册期中专题复习(Word版含解析) |  | |
| 格式 | docx | ||
| 文件大小 | 415.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-10-20 15:36:50 | ||
图片预览

文档简介
13.1轴对称2021-2022学年度人教版八年级数学上册期中专题复习
一、选择题
1.现实世界中,对称现象无处不在.下列汉字是轴对称图形的是( )
A.爱 B.我 C.中 D.华
2.下列图案是几家银行的标志,其中是轴对称图形的有( )
A.1个 B.2个 C.3个 D.4个
3.下列条件中,不能判定直线CD是线段AB(C,D不在线段AB上)的垂直平分线的是( )
A.CA=CB,DA=DB B.CA=CB,CD⊥AB
C.CA=DA,CB=DB D.CA=CB,CD平分AB
4.如图,在中,,的垂直平分线交于点,交边于点,的周长等于,则的长等于( )
A. B. C. D.
5.如图,在直角三角形纸片ABC中,∠ACB=90°,∠A=40°,将纸片沿着CD折叠,使AC边与BC边重合,则∠的度数为( )
A.10° B.20° C.30° D.40°
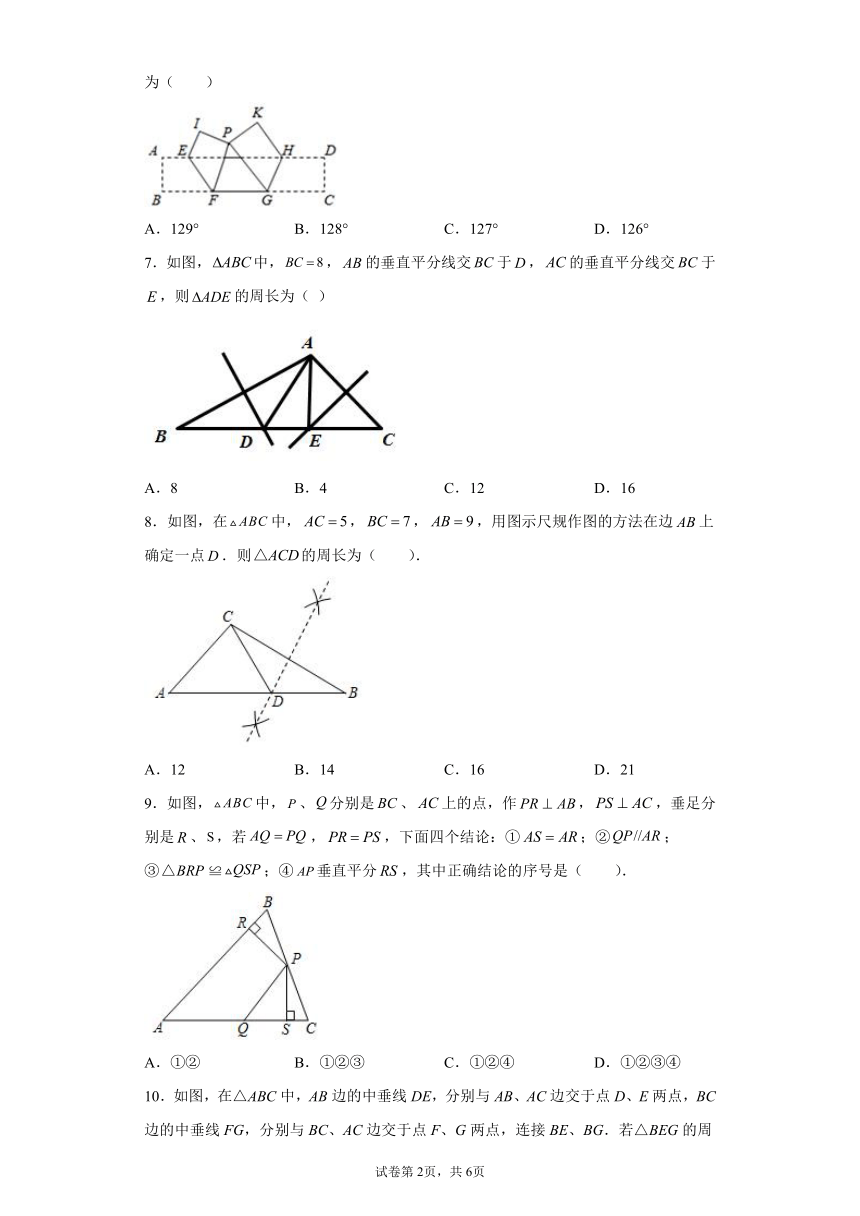
6.如图,已知长方形纸片ABCD,点E、H在AD边上,点F,G在BC边上,分别沿EF,GH折叠,使点B和点C都落在点P处,若,则∠IPK的度数为( )
A.129° B.128° C.127° D.126°
7.如图,中,,的垂直平分线交于,的垂直平分线交于,则的周长为( )
A.8 B.4 C.12 D.16
8.如图,在中,,,,用图示尺规作图的方法在边上确定一点.则的周长为( ).
A.12 B.14 C.16 D.21
9.如图,中,、分别是、上的点,作,,垂足分别是、,若,,下面四个结论:①;②;③≌;④垂直平分,其中正确结论的序号是( ).
A.①② B.①②③ C.①②④ D.①②③④
10.如图,在△ABC中,AB边的中垂线DE,分别与AB、AC边交于点D、E两点,BC边的中垂线FG,分别与BC、AC边交于点F、G两点,连接BE、BG.若△BEG的周长为16,GE=1.则AC的长为( )
A.13 B.14 C.15 D.16
二、填空题
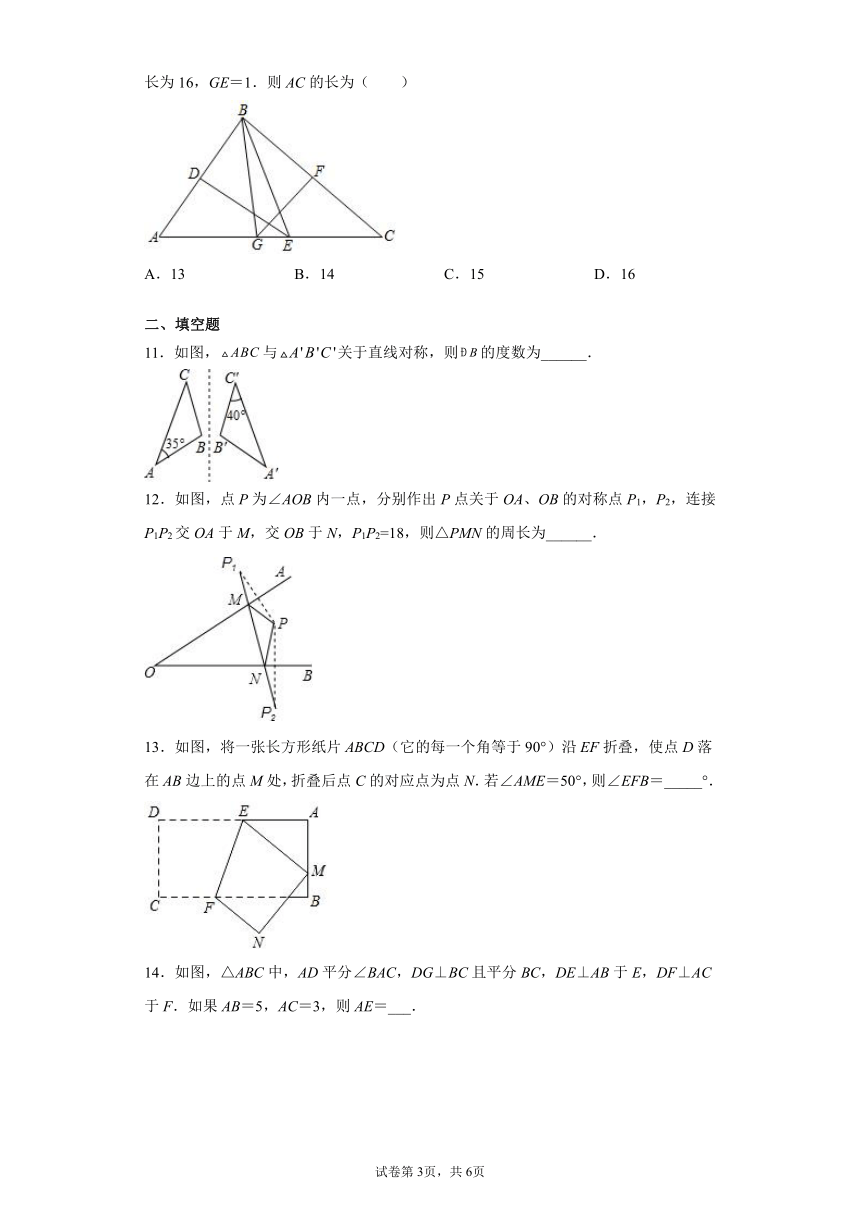
11.如图,与关于直线对称,则的度数为______.
12.如图,点P为∠AOB内一点,分别作出P点关于OA、OB的对称点P1,P2,连接P1P2交OA于M,交OB于N,P1P2=18,则△PMN的周长为______.
13.如图,将一张长方形纸片ABCD(它的每一个角等于90°)沿EF折叠,使点D落在AB边上的点M处,折叠后点C的对应点为点N.若∠AME=50°,则∠EFB=_____°.
14.如图,△ABC中,AD平分∠BAC,DG⊥BC且平分BC,DE⊥AB于E,DF⊥AC于F.如果AB=5,AC=3,则AE=___.
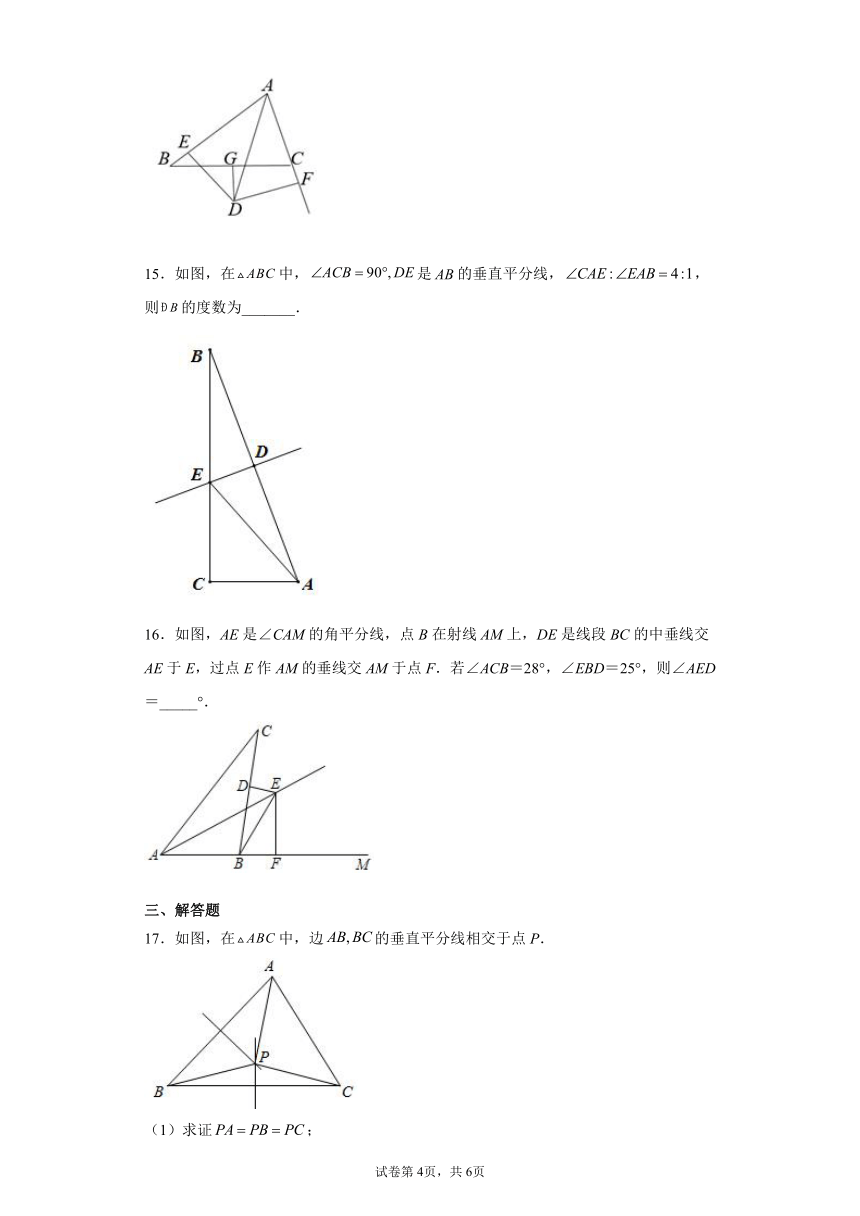
15.如图,在中,是的垂直平分线,,则的度数为_______.
16.如图,AE是∠CAM的角平分线,点B在射线AM上,DE是线段BC的中垂线交AE于E,过点E作AM的垂线交AM于点F.若∠ACB=28°,∠EBD=25°,则∠AED=_____°.
三、解答题
17.如图,在中,边的垂直平分线相交于点P.
(1)求证;
(2)点P是否也在边的垂直平分线上?由此你还能得出什么结论?
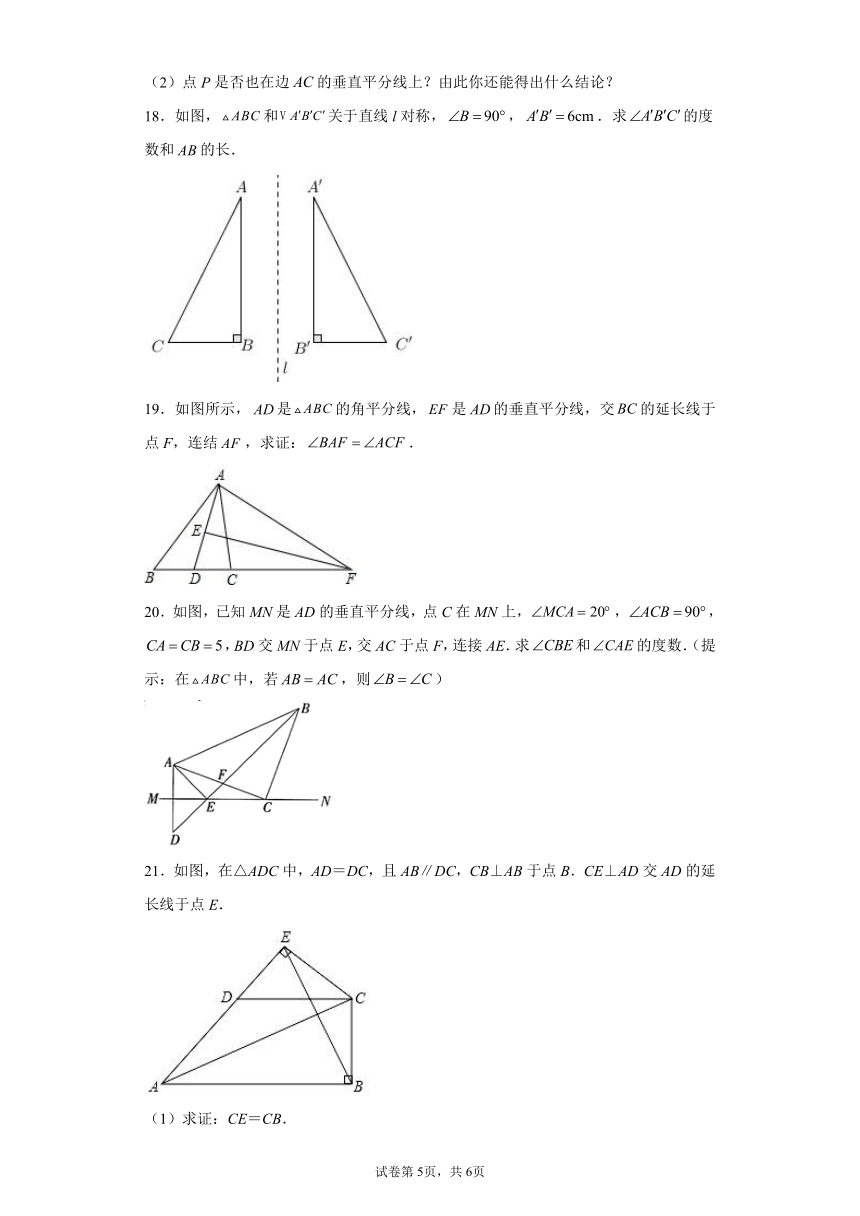
18.如图,和关于直线l对称,,.求的度数和的长.
19.如图所示,是的角平分线,是的垂直平分线,交的延长线于点F,连结,求证:.
20.如图,已知MN是AD的垂直平分线,点C在MN上,,,,BD交MN于点E,交AC于点F,连接AE.求和的度数.(提示:在中,若,则)
21.如图,在△ADC中,AD=DC,且AB∥DC,CB⊥AB于点B.CE⊥AD交AD的延长线于点E.
(1)求证:CE=CB.
(2)连接BE,求证:AC垂直平分BE.
试卷第1页,共3页
试卷第1页,共3页
参考答案
1.C
“中”能找到这样的一条直线,使这个图形沿一条直线折叠,直线两旁的部分能够互相重合,所以这个图形是轴对称图形;
“爱”,“我”,“华”不能找到这样的一条直线,使这些图形沿一条直线折叠,直线两旁的部分能够互相重合,所以这些图形不是轴对称图形;
故选:C.
2.C
解:都是轴对称图形,而不是轴对称图形,所以是轴对称图形的有3个;
故选C.
3.C
解:A、CA=CB,DA=DB,可以判定直线CD是线段AB(C,D不在线段AB上)的垂直平分线,不符合题意;
B、CA=CB,CD⊥AB,可以判定直线CD是线段AB(C,D不在线段AB上)的垂直平分线,不符合题意;
C、CA=DA,CB=DB,不能判定直线CD是线段AB(C,D不在线段AB上)的垂直平分线,符合题意;
D、CA=CB,CD平分AB,可以判定直线CD是线段AB(C,D不在线段AB上)的垂直平分线,不符合题意.
故选:C.
4.B
解:∵DE是边AB的垂直平分线,
∴AE=BE.
∴△BCE的周长=BC+BE+CE=BC+AE+CE=BC+AC=18.
又∵BC=8,
∴AC=10(cm).
故选:B.
5.A
解:∵∠ACB=90°,∠A=40°,
∴,
由折叠的性质可知,
∴;
故选A.
6.B
由折叠和矩形的性质可知:,,.
∵,
∴.
∵,
∴,
∴,
∴.
故选:B.
7.A
线段AB的垂直平分线交BC于点D,
线段AC的垂直平分线交BC于点F,
,
的周长,
故选:A.
8.B
解:根据题意得:尺规作图的方法所作的直线是 的垂直平分线,
∴ ,
∵,
∴ ,
∵,
∴的周长为 .
故选:B.
9.C
解:如图,连接AP,RS,
∵PR⊥AB,PS⊥AC,
∴∠ARP=∠ASP=90°,
∵AP=AP,PR=PS,
∴Rt△APR≌Rt△APS(HL),
∴AS=AR,∠PAR=∠PAS,故①正确,
∵AQ=PQ,
∴∠QAP=∠QPA,
∴∠RAP=∠QPA,
∴QP∥AR,故②正确,
∵AR=AS,PR=PS,
∴AP垂直平分RS,故④正确,
由题目条件不能证明△BRP≌△QSP,
故选:C.
10.B
解:∵DE是线段AB的中垂线,GF是线段BC的中垂线,
∴EB=EA,GB=GC,
∵△BEG周长为16,
∴EB+GB+EG=16,
∴EA+GC+EG=16,
∴GA+EG+EG+EG+EC=16,
∴AC+2EG=16,
∵EG=1,
∴AC=14,
故选:B.
11.105°
解:∵△ABC与△A′B′C′关于直线l对称,
∴∠C=∠C′=40°,
∴∠B=180°-∠A-∠C
=180°-40°-35°
=105°.
故答案为:105°.
12.18
解:∵P,P1关于OA对称,P,P2关于OB对称,
∴PN=NP2,MP=MP1,
∴△PMN的周长=PN+MN+PM=NP2+MN+MP1=P1P2=18,
∴△PMN的周长为18.
故答案为:18.
13.70
解:∵长方形纸片ABCD(它的每一个角等于90°)沿EF折叠,
∴∠DEF=∠MEF,∠A=90°,∠EFB=∠DEF,
∵∠AME=50°,
∴∠AEM=90°﹣∠AME=90°﹣50°=40°,
∴∠DEM=180°﹣∠AEM=180°﹣40°=140°,
∴∠DEF=∠MEF=.
∴∠EFB=70°,
故填:70.
14.4
解:连接BD,CD,
∵AD平分∠BAC,DE⊥AB,DF⊥AC,
∴DE=DF,∠BED=∠CFD=90°,
∵DG⊥BC且平分BC,
∴BD=CD,
∴在与中,,
∴,
∴BE=CF,
∴在△AED和△AFD中,,
∴△AED≌△AFD(AAS),
∴AE=AF,
设BE=x,则CF=x,
∵AB=5,AC=3,AE=AB-BE,AF=AC+CF,
∴,
解得:x=1,
∴BE=1,
∴AE=AB-BE=5-1=4,
故答案为:4.
15.15°
解:∵在Rt△ABC中,,
∵DE是AB的垂直平分线
∴∠B=∠BAE
∵∠CAE:∠EAB=4:1
∴6∠B=90°
∴∠B=15°
故答案为:15°.
16.37
解:连接CE,过E作ER⊥AC于R,CD交ER于Q,AE交BC于O,
∵DE是线段BC的中垂线,
∴∠EDC=90°,CE=BE,
∴∠ECB=∠EBD,
∵∠EBD=25°,
∴∠ECB=25°,
∴∠DEB=∠CED=90°﹣25°=65°,
∵ER⊥AC,ED⊥BC,
∴∠QRC=∠QDE=90°,
∴∠ACB+∠CQR=90°,∠EQD+∠QED=90°,
∵∠CQR=∠EQD,
∴∠ACB=∠QED,
∵∠ACB=28°,
∴∠QED=28°,
∵AE平分∠CAM,ER⊥AC,EF⊥AM,
∴ER=EF,
在Rt△ERC和Rt△EFB中,
,
∴Rt△ERC≌Rt△EFB(HL),
∴∠EBF=∠ACE=∠ACB+∠ECD=28°+25°=53°,
∵∠EFB=90°,
∴∠BEF=90°﹣∠EBF=90°﹣53°=37°,
∴∠REF=∠RED+∠BED+∠BEF=28°+65°+37°=130°,
∵∠ARE=∠AFE=90°,
∴∠CAM=360°﹣90°﹣90°﹣130°=50°,
∵AE平分∠CAM,
∴∠CAE=CAM=25°,
∴∠DOE=∠CAE+∠ACB=25°+28°=53°,
∵ED⊥BC,
∴∠EDB=90°,
∴∠AED=90°﹣∠DOE=90°﹣53°=37°,
故答案为:37.
17.
解:(1)∵点P是的垂直平分线上的点,
∴.
同理.
∴.
(2)∵PA=PC,
∴点P在边AC的垂直平分线上(和一条线段的两个端点的距离相等的点,在这条线段的垂直平分线上)
还可得出结论:①三角形三边的垂直平分线相交于一点.②这个点与三顶点距离相等.
点P也在边的垂直平分线上,由此可以得出,三角形三条边的垂直平分线相交于一点.
18.
解:∵△ABC和△A′B′C′关于直线l对称,
∴△ABC≌△A′B′C′.
∴,.
19证明:∵EF是AD的垂直平分线,
∴AF=DF,
∴∠FAD=∠ADF,
∵∠FAD=∠FAC+∠CAD,∠ADF=∠B+∠DAB,
∵AD是∠BAC的平分线,
∴∠DAB=∠CAD,
∴∠FAC=∠B,
∴∠BAC+∠FAC=∠B+∠BAC,
即∠BAF=∠ACF.
20.,
解:如图,连接CD,
∵MN垂直平分AD,点C、E在MN上,根据点A、D关于MN的对称性,得,,,
∵,∴,
∴,∴,
∵,∴,
∵,∴,
∴,
.
21.
(1)∵AD=CD,
∴∠DAC=∠DCA,
∵AB∥CD,
∴∠DCA=∠CAB,
∴∠DAC=∠CAB,
∴AC是∠EAB的角平分线,
∵CE⊥AE,CB⊥AB,
∴CE=CB;
(2)由(1)知,CE=CB,
∵CE⊥AE,CB⊥AB,
∴∠CEA=∠CBA=90°,
在Rt△CEA和Rt△CBA中,
,
∴Rt△CEA≌Rt△CBA(HL),
∴AE=AB,CE=CB,
∴点A、点C在线段BE的垂直平分线上,
∴AC垂直平分BE.
答案第1页,共2页
答案第1页,共2页
一、选择题
1.现实世界中,对称现象无处不在.下列汉字是轴对称图形的是( )
A.爱 B.我 C.中 D.华
2.下列图案是几家银行的标志,其中是轴对称图形的有( )
A.1个 B.2个 C.3个 D.4个
3.下列条件中,不能判定直线CD是线段AB(C,D不在线段AB上)的垂直平分线的是( )
A.CA=CB,DA=DB B.CA=CB,CD⊥AB
C.CA=DA,CB=DB D.CA=CB,CD平分AB
4.如图,在中,,的垂直平分线交于点,交边于点,的周长等于,则的长等于( )
A. B. C. D.
5.如图,在直角三角形纸片ABC中,∠ACB=90°,∠A=40°,将纸片沿着CD折叠,使AC边与BC边重合,则∠的度数为( )
A.10° B.20° C.30° D.40°
6.如图,已知长方形纸片ABCD,点E、H在AD边上,点F,G在BC边上,分别沿EF,GH折叠,使点B和点C都落在点P处,若,则∠IPK的度数为( )
A.129° B.128° C.127° D.126°
7.如图,中,,的垂直平分线交于,的垂直平分线交于,则的周长为( )
A.8 B.4 C.12 D.16
8.如图,在中,,,,用图示尺规作图的方法在边上确定一点.则的周长为( ).
A.12 B.14 C.16 D.21
9.如图,中,、分别是、上的点,作,,垂足分别是、,若,,下面四个结论:①;②;③≌;④垂直平分,其中正确结论的序号是( ).
A.①② B.①②③ C.①②④ D.①②③④
10.如图,在△ABC中,AB边的中垂线DE,分别与AB、AC边交于点D、E两点,BC边的中垂线FG,分别与BC、AC边交于点F、G两点,连接BE、BG.若△BEG的周长为16,GE=1.则AC的长为( )
A.13 B.14 C.15 D.16
二、填空题
11.如图,与关于直线对称,则的度数为______.
12.如图,点P为∠AOB内一点,分别作出P点关于OA、OB的对称点P1,P2,连接P1P2交OA于M,交OB于N,P1P2=18,则△PMN的周长为______.
13.如图,将一张长方形纸片ABCD(它的每一个角等于90°)沿EF折叠,使点D落在AB边上的点M处,折叠后点C的对应点为点N.若∠AME=50°,则∠EFB=_____°.
14.如图,△ABC中,AD平分∠BAC,DG⊥BC且平分BC,DE⊥AB于E,DF⊥AC于F.如果AB=5,AC=3,则AE=___.
15.如图,在中,是的垂直平分线,,则的度数为_______.
16.如图,AE是∠CAM的角平分线,点B在射线AM上,DE是线段BC的中垂线交AE于E,过点E作AM的垂线交AM于点F.若∠ACB=28°,∠EBD=25°,则∠AED=_____°.
三、解答题
17.如图,在中,边的垂直平分线相交于点P.
(1)求证;
(2)点P是否也在边的垂直平分线上?由此你还能得出什么结论?
18.如图,和关于直线l对称,,.求的度数和的长.
19.如图所示,是的角平分线,是的垂直平分线,交的延长线于点F,连结,求证:.
20.如图,已知MN是AD的垂直平分线,点C在MN上,,,,BD交MN于点E,交AC于点F,连接AE.求和的度数.(提示:在中,若,则)
21.如图,在△ADC中,AD=DC,且AB∥DC,CB⊥AB于点B.CE⊥AD交AD的延长线于点E.
(1)求证:CE=CB.
(2)连接BE,求证:AC垂直平分BE.
试卷第1页,共3页
试卷第1页,共3页
参考答案
1.C
“中”能找到这样的一条直线,使这个图形沿一条直线折叠,直线两旁的部分能够互相重合,所以这个图形是轴对称图形;
“爱”,“我”,“华”不能找到这样的一条直线,使这些图形沿一条直线折叠,直线两旁的部分能够互相重合,所以这些图形不是轴对称图形;
故选:C.
2.C
解:都是轴对称图形,而不是轴对称图形,所以是轴对称图形的有3个;
故选C.
3.C
解:A、CA=CB,DA=DB,可以判定直线CD是线段AB(C,D不在线段AB上)的垂直平分线,不符合题意;
B、CA=CB,CD⊥AB,可以判定直线CD是线段AB(C,D不在线段AB上)的垂直平分线,不符合题意;
C、CA=DA,CB=DB,不能判定直线CD是线段AB(C,D不在线段AB上)的垂直平分线,符合题意;
D、CA=CB,CD平分AB,可以判定直线CD是线段AB(C,D不在线段AB上)的垂直平分线,不符合题意.
故选:C.
4.B
解:∵DE是边AB的垂直平分线,
∴AE=BE.
∴△BCE的周长=BC+BE+CE=BC+AE+CE=BC+AC=18.
又∵BC=8,
∴AC=10(cm).
故选:B.
5.A
解:∵∠ACB=90°,∠A=40°,
∴,
由折叠的性质可知,
∴;
故选A.
6.B
由折叠和矩形的性质可知:,,.
∵,
∴.
∵,
∴,
∴,
∴.
故选:B.
7.A
线段AB的垂直平分线交BC于点D,
线段AC的垂直平分线交BC于点F,
,
的周长,
故选:A.
8.B
解:根据题意得:尺规作图的方法所作的直线是 的垂直平分线,
∴ ,
∵,
∴ ,
∵,
∴的周长为 .
故选:B.
9.C
解:如图,连接AP,RS,
∵PR⊥AB,PS⊥AC,
∴∠ARP=∠ASP=90°,
∵AP=AP,PR=PS,
∴Rt△APR≌Rt△APS(HL),
∴AS=AR,∠PAR=∠PAS,故①正确,
∵AQ=PQ,
∴∠QAP=∠QPA,
∴∠RAP=∠QPA,
∴QP∥AR,故②正确,
∵AR=AS,PR=PS,
∴AP垂直平分RS,故④正确,
由题目条件不能证明△BRP≌△QSP,
故选:C.
10.B
解:∵DE是线段AB的中垂线,GF是线段BC的中垂线,
∴EB=EA,GB=GC,
∵△BEG周长为16,
∴EB+GB+EG=16,
∴EA+GC+EG=16,
∴GA+EG+EG+EG+EC=16,
∴AC+2EG=16,
∵EG=1,
∴AC=14,
故选:B.
11.105°
解:∵△ABC与△A′B′C′关于直线l对称,
∴∠C=∠C′=40°,
∴∠B=180°-∠A-∠C
=180°-40°-35°
=105°.
故答案为:105°.
12.18
解:∵P,P1关于OA对称,P,P2关于OB对称,
∴PN=NP2,MP=MP1,
∴△PMN的周长=PN+MN+PM=NP2+MN+MP1=P1P2=18,
∴△PMN的周长为18.
故答案为:18.
13.70
解:∵长方形纸片ABCD(它的每一个角等于90°)沿EF折叠,
∴∠DEF=∠MEF,∠A=90°,∠EFB=∠DEF,
∵∠AME=50°,
∴∠AEM=90°﹣∠AME=90°﹣50°=40°,
∴∠DEM=180°﹣∠AEM=180°﹣40°=140°,
∴∠DEF=∠MEF=.
∴∠EFB=70°,
故填:70.
14.4
解:连接BD,CD,
∵AD平分∠BAC,DE⊥AB,DF⊥AC,
∴DE=DF,∠BED=∠CFD=90°,
∵DG⊥BC且平分BC,
∴BD=CD,
∴在与中,,
∴,
∴BE=CF,
∴在△AED和△AFD中,,
∴△AED≌△AFD(AAS),
∴AE=AF,
设BE=x,则CF=x,
∵AB=5,AC=3,AE=AB-BE,AF=AC+CF,
∴,
解得:x=1,
∴BE=1,
∴AE=AB-BE=5-1=4,
故答案为:4.
15.15°
解:∵在Rt△ABC中,,
∵DE是AB的垂直平分线
∴∠B=∠BAE
∵∠CAE:∠EAB=4:1
∴6∠B=90°
∴∠B=15°
故答案为:15°.
16.37
解:连接CE,过E作ER⊥AC于R,CD交ER于Q,AE交BC于O,
∵DE是线段BC的中垂线,
∴∠EDC=90°,CE=BE,
∴∠ECB=∠EBD,
∵∠EBD=25°,
∴∠ECB=25°,
∴∠DEB=∠CED=90°﹣25°=65°,
∵ER⊥AC,ED⊥BC,
∴∠QRC=∠QDE=90°,
∴∠ACB+∠CQR=90°,∠EQD+∠QED=90°,
∵∠CQR=∠EQD,
∴∠ACB=∠QED,
∵∠ACB=28°,
∴∠QED=28°,
∵AE平分∠CAM,ER⊥AC,EF⊥AM,
∴ER=EF,
在Rt△ERC和Rt△EFB中,
,
∴Rt△ERC≌Rt△EFB(HL),
∴∠EBF=∠ACE=∠ACB+∠ECD=28°+25°=53°,
∵∠EFB=90°,
∴∠BEF=90°﹣∠EBF=90°﹣53°=37°,
∴∠REF=∠RED+∠BED+∠BEF=28°+65°+37°=130°,
∵∠ARE=∠AFE=90°,
∴∠CAM=360°﹣90°﹣90°﹣130°=50°,
∵AE平分∠CAM,
∴∠CAE=CAM=25°,
∴∠DOE=∠CAE+∠ACB=25°+28°=53°,
∵ED⊥BC,
∴∠EDB=90°,
∴∠AED=90°﹣∠DOE=90°﹣53°=37°,
故答案为:37.
17.
解:(1)∵点P是的垂直平分线上的点,
∴.
同理.
∴.
(2)∵PA=PC,
∴点P在边AC的垂直平分线上(和一条线段的两个端点的距离相等的点,在这条线段的垂直平分线上)
还可得出结论:①三角形三边的垂直平分线相交于一点.②这个点与三顶点距离相等.
点P也在边的垂直平分线上,由此可以得出,三角形三条边的垂直平分线相交于一点.
18.
解:∵△ABC和△A′B′C′关于直线l对称,
∴△ABC≌△A′B′C′.
∴,.
19证明:∵EF是AD的垂直平分线,
∴AF=DF,
∴∠FAD=∠ADF,
∵∠FAD=∠FAC+∠CAD,∠ADF=∠B+∠DAB,
∵AD是∠BAC的平分线,
∴∠DAB=∠CAD,
∴∠FAC=∠B,
∴∠BAC+∠FAC=∠B+∠BAC,
即∠BAF=∠ACF.
20.,
解:如图,连接CD,
∵MN垂直平分AD,点C、E在MN上,根据点A、D关于MN的对称性,得,,,
∵,∴,
∴,∴,
∵,∴,
∵,∴,
∴,
.
21.
(1)∵AD=CD,
∴∠DAC=∠DCA,
∵AB∥CD,
∴∠DCA=∠CAB,
∴∠DAC=∠CAB,
∴AC是∠EAB的角平分线,
∵CE⊥AE,CB⊥AB,
∴CE=CB;
(2)由(1)知,CE=CB,
∵CE⊥AE,CB⊥AB,
∴∠CEA=∠CBA=90°,
在Rt△CEA和Rt△CBA中,
,
∴Rt△CEA≌Rt△CBA(HL),
∴AE=AB,CE=CB,
∴点A、点C在线段BE的垂直平分线上,
∴AC垂直平分BE.
答案第1页,共2页
答案第1页,共2页
