13.2画轴对称图形2021-2022学年度人教版八年级数学上册期中专题复习(Word版含解析)
文档属性
| 名称 | 13.2画轴对称图形2021-2022学年度人教版八年级数学上册期中专题复习(Word版含解析) | 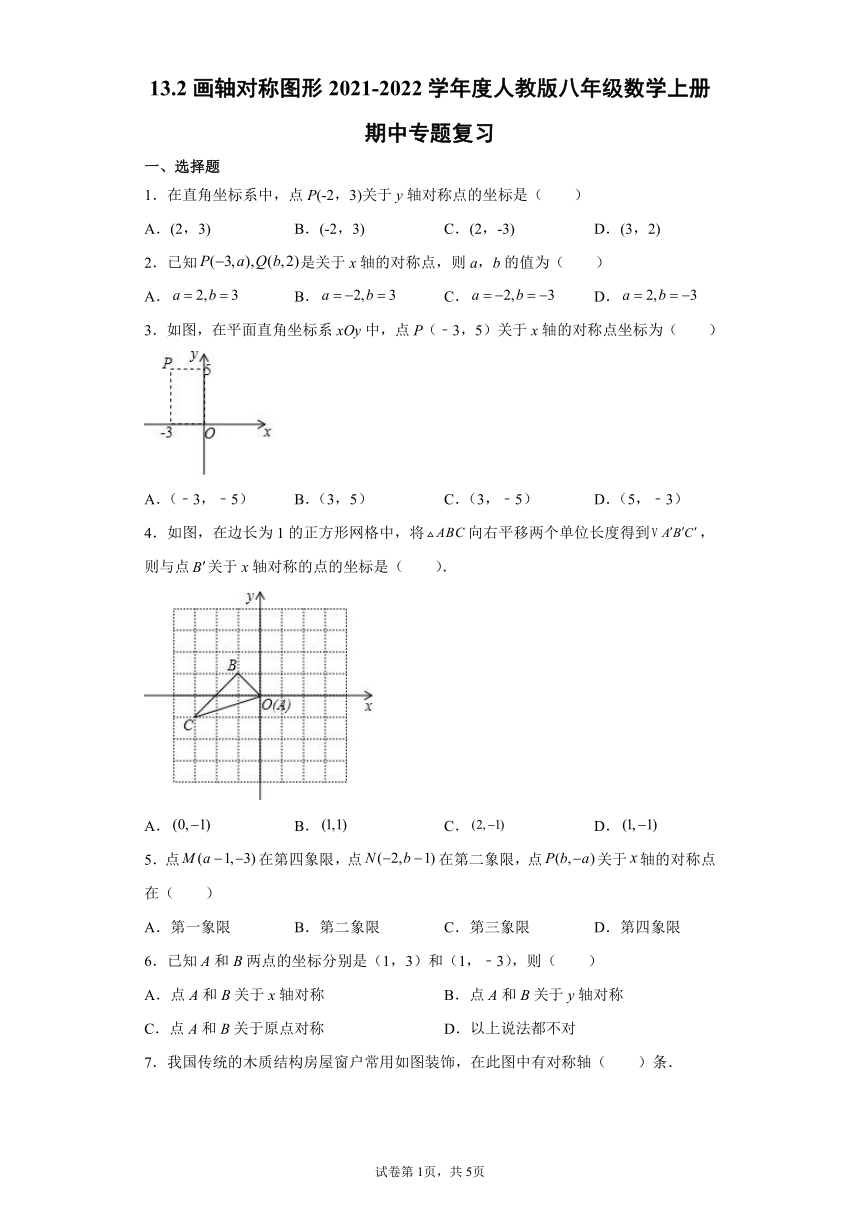 | |
| 格式 | docx | ||
| 文件大小 | 474.3KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-10-20 15:47:49 | ||
图片预览




文档简介
13.2画轴对称图形2021-2022学年度人教版八年级数学上册期中专题复习
一、选择题
1.在直角坐标系中,点P(-2,3)关于y轴对称点的坐标是( )
A.(2,3) B.(-2,3) C.(2,-3) D.(3,2)
2.已知是关于x轴的对称点,则a,b的值为( )
A. B. C. D.
3.如图,在平面直角坐标系xOy中,点P(﹣3,5)关于x轴的对称点坐标为( )
A.(﹣3,﹣5) B.(3,5) C.(3,﹣5) D.(5,﹣3)
4.如图,在边长为1的正方形网格中,将向右平移两个单位长度得到,则与点关于x轴对称的点的坐标是( ).
A. B. C. D.
5.点在第四象限,点在第二象限,点关于轴的对称点在( )
A.第一象限 B.第二象限 C.第三象限 D.第四象限
6.已知A和B两点的坐标分别是(1,3)和(1,﹣3),则( )
A.点A和B关于x轴对称 B.点A和B关于y轴对称
C.点A和B关于原点对称 D.以上说法都不对
7.我国传统的木质结构房屋窗户常用如图装饰,在此图中有对称轴( )条.
A.1 B.2 C.3 D.4
8.在平面直角坐标系中,点A(2,m)和点B(n,3)关于轴对称,则的值为( )
A.5 B.﹣5 C.1 D.﹣1
9.在平面直角坐标系中,把点P先向左平移7个单位长度,再向上平移5个单位长度得到点M,作点M关于y轴的对称点N.已知点N的坐标是(5,1),那么点P的坐标是 ( )
A.(2,-4) B.(6,-4) C.(6,-1) D.(2,-1)
10.如图,在3×3的正方形网格中,图中的△ABC为格点三角形,在图中与△ABC成轴对称的格点三角形可以找出( )个
A.6个 B.5个 C.4个 D.3个
二、填空题
11.已知直角坐标系中点和点B(3,b)关于x轴对称,则b-a=_____________.
12.如图,边长均为1个单位的正方形组成的方格纸内有一张笑脸图案,已知左眼的坐标是(﹣1,0),那么右眼关于鼻子所在的水平线对称的点的坐标是___.
13.如图,在3×3的正方形网格中有两个小正方形被涂黑,再将图中其余小正方形任意一个涂黑,使得整个图形(包括网格)构成一个轴对称图形,那么涂法共有________种.
14.点关于轴对称的点的坐标是,则______.
15.在平面直角坐标系中,点关于轴的对称点为,将点向左平移3个单位得到点,则的坐标为__________.
16.在平面直角坐标系中,已知点A(0,2)、B(2,0)、C(3,1),在坐标系中画出一个△A1B1C1,使得△A1B1C1≌△ABC,则A1、B1、C1的坐标分别为_______.
三、解答题
17.已知:如图,在平面直角坐标系中.
(1)作出关于y轴对称的,并写出三个顶点的坐标:(______),(______),(______);
(2)作出关于x轴对称的,并写出三个顶点的坐标:(______),(______),(______);
(3)求出的面积.
18.如图,在正方形网格中,每个小正方形的边长都是1,每个小正方形的顶点叫做格点.网格中有一个格点△ABC(即三角形的顶点都在格点上).
(1)在图中画出△A1B1C1,使它与△ABC关于直线l对称;
(2)在直线l上找一点P,使得PA+PC最小;
(3)△ABC的面积为 .
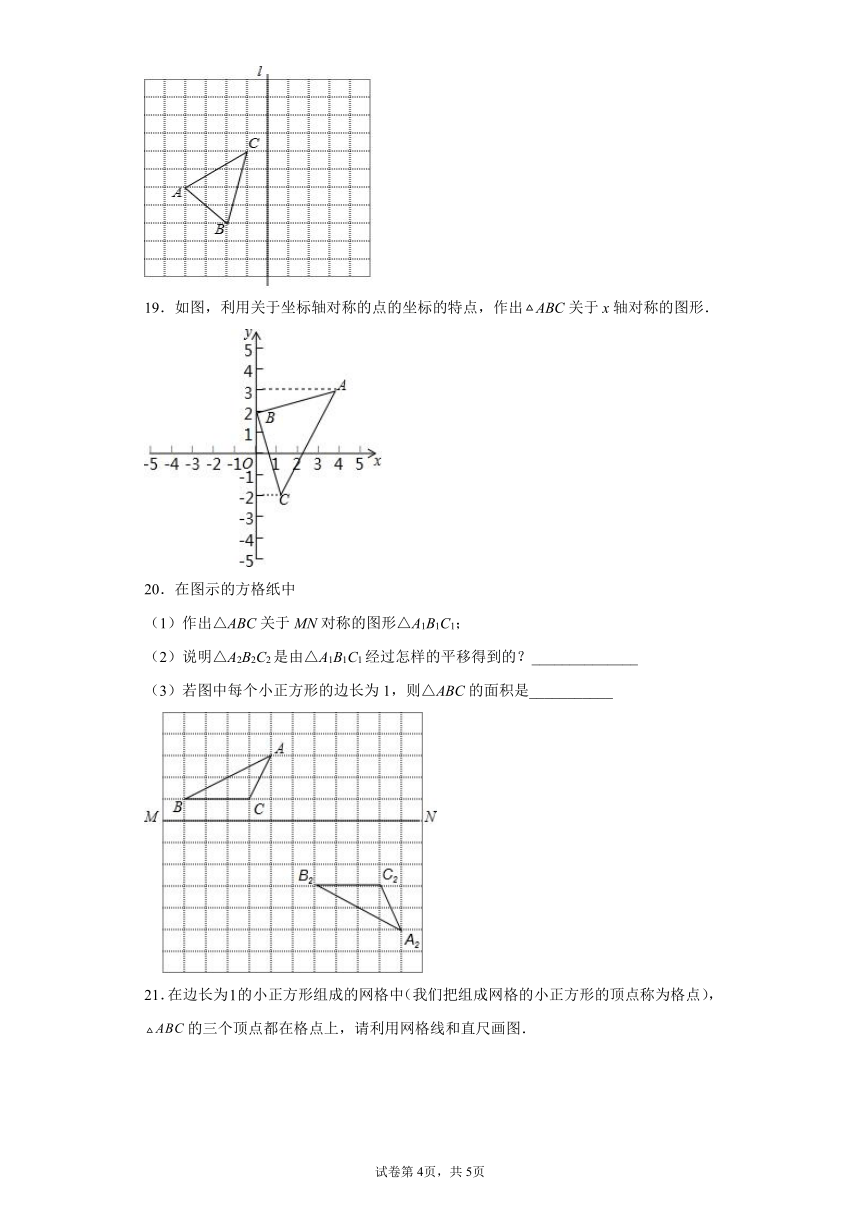
19.如图,利用关于坐标轴对称的点的坐标的特点,作出ABC关于x轴对称的图形.
20.在图示的方格纸中
(1)作出△ABC关于MN对称的图形△A1B1C1;
(2)说明△A2B2C2是由△A1B1C1经过怎样的平移得到的?______________
(3)若图中每个小正方形的边长为1,则△ABC的面积是___________
21.在边长为的小正方形组成的网格中(我们把组成网格的小正方形的顶点称为格点),的三个顶点都在格点上,请利用网格线和直尺画图.
(1)在图中画出关于直线成轴对称的;
(2)求出的面积;
(3)在所给的网格内,在直线上找一点,使的面积等于的面积.
试卷第1页,共3页
试卷第1页,共3页
参考答案
1.A
解:根据关于轴对称的点,纵坐标相同,横坐标互为相反数,
点关于轴的对称点坐标为.
故选:A.
2.C
解:∵是关于x轴的对称点,
∴,
故选C.
3.A
解:点P( 3,5)关于x轴的对称点坐标为( 3, 5),
故选:A.
4.D
解:,
向右平移两个单位长度得到,
关于x轴对称的点的坐标为:.
故选:D.
5.A
解:∵点在第四象限,点在第二象限,
∴,
∴,
∴,
∴在第四象限,
∵关于x轴对称的点的坐标为
∴关于x轴对称的点在第一象限,
故选A.
6.A
解:∵A和B两点的坐标分别是(1,3)和(1,-3),
∴A和B两点的横坐标相同,纵坐标互为相反数,
∴点A和B关于x轴对称.
故选:A.
7.B
解:这是一个组合图形,它的外部是一个长方形,再根据它的组合特点,显然有2条对称轴,即两组对边的垂直平分线.
故答案选:B
8.C
解:因为点A(2,m)和点B(n,3)关于轴对称,
所以m=-3,n=2,
所以.
故选C.
9.A
解:因为点M和点N关于y轴对称,N点坐标是(5,1),
所以点M是(-5,1),
又因为点P先向左平移7个单位长度,再向上平移5个单位长度得到点M,
所以点P是(2,-4),
故选A.
10.A
解:如图,最多能画出6个格点三角形与△ABC成轴对称.
故选:A.
11.
解:点和点,点和点关于轴对称,
,,
,
故答案为:.
12.
左眼的坐标是(﹣1,0),
以两眼的中点为原点,两眼所在的直线为轴,竖直方向为轴,分别以向右和向上为正方向建立平面直角坐标系,如图,
则点即为所求,
故答案为:
13.5
解:如图所示:所标数字之处都可以构成轴对称图形.
故答案为:5.
14.1
点关于轴对称的点的坐标是,
,
解得
故答案为:
15.
解:由点关于轴的对称点为可得:,
∴将点向左平移3个单位得到点,则的坐标为;
故答案为.
16.A1(0,2)、B1(-2,0)、C1(-3,1)(答案不唯一).
解:画图如下:
∵△A1B1C1≌△ABC,
∴△A1B1C1与△ABC关y轴对称,
∵A(0,2)、B(2,0)、C(3,1),
∴A1(0,2)、B1(-2,0)、C1(-3,1)
故答案为:A1(0,2)、B1(-2,0)、C1(-3,1).
17.
(1)作出关于y轴对称的如图所示,
,,,
,,;
(2)作出关于x轴对称的如图所示,
,,,
,,;
(3)如图所示: ,
.
18.
解:(1)如图所示,△A1B1C1即为所求.
(2)连接AC1,则AC1与l的交点P即为所求的点.
(3)△ABC的面积=3×4﹣×1×4﹣×2×2﹣×2×3=5,
故答案为:5.
19.
解:如图所示,即为所求.
20.
(1)△A1B1C1如图所示;
(2)根据图形可知,△A2B2C2是由△A1B1C1向右平移6个单位,再向下平移2个单位(或向下平移2个单位,再向右平移6个单位).
故答案为:向右平移6个单位,再向下平移2个单位(或向下平移2个单位,再向右平移6个单位)
(3)
故答案为:3
21.
解:(1)如图,即为所求;
(2)连接,,
;
(3)过点B作AC的平行线交直线m于点P,则点P即为所求,如图示.
答案第1页,共2页
答案第1页,共2页
一、选择题
1.在直角坐标系中,点P(-2,3)关于y轴对称点的坐标是( )
A.(2,3) B.(-2,3) C.(2,-3) D.(3,2)
2.已知是关于x轴的对称点,则a,b的值为( )
A. B. C. D.
3.如图,在平面直角坐标系xOy中,点P(﹣3,5)关于x轴的对称点坐标为( )
A.(﹣3,﹣5) B.(3,5) C.(3,﹣5) D.(5,﹣3)
4.如图,在边长为1的正方形网格中,将向右平移两个单位长度得到,则与点关于x轴对称的点的坐标是( ).
A. B. C. D.
5.点在第四象限,点在第二象限,点关于轴的对称点在( )
A.第一象限 B.第二象限 C.第三象限 D.第四象限
6.已知A和B两点的坐标分别是(1,3)和(1,﹣3),则( )
A.点A和B关于x轴对称 B.点A和B关于y轴对称
C.点A和B关于原点对称 D.以上说法都不对
7.我国传统的木质结构房屋窗户常用如图装饰,在此图中有对称轴( )条.
A.1 B.2 C.3 D.4
8.在平面直角坐标系中,点A(2,m)和点B(n,3)关于轴对称,则的值为( )
A.5 B.﹣5 C.1 D.﹣1
9.在平面直角坐标系中,把点P先向左平移7个单位长度,再向上平移5个单位长度得到点M,作点M关于y轴的对称点N.已知点N的坐标是(5,1),那么点P的坐标是 ( )
A.(2,-4) B.(6,-4) C.(6,-1) D.(2,-1)
10.如图,在3×3的正方形网格中,图中的△ABC为格点三角形,在图中与△ABC成轴对称的格点三角形可以找出( )个
A.6个 B.5个 C.4个 D.3个
二、填空题
11.已知直角坐标系中点和点B(3,b)关于x轴对称,则b-a=_____________.
12.如图,边长均为1个单位的正方形组成的方格纸内有一张笑脸图案,已知左眼的坐标是(﹣1,0),那么右眼关于鼻子所在的水平线对称的点的坐标是___.
13.如图,在3×3的正方形网格中有两个小正方形被涂黑,再将图中其余小正方形任意一个涂黑,使得整个图形(包括网格)构成一个轴对称图形,那么涂法共有________种.
14.点关于轴对称的点的坐标是,则______.
15.在平面直角坐标系中,点关于轴的对称点为,将点向左平移3个单位得到点,则的坐标为__________.
16.在平面直角坐标系中,已知点A(0,2)、B(2,0)、C(3,1),在坐标系中画出一个△A1B1C1,使得△A1B1C1≌△ABC,则A1、B1、C1的坐标分别为_______.
三、解答题
17.已知:如图,在平面直角坐标系中.
(1)作出关于y轴对称的,并写出三个顶点的坐标:(______),(______),(______);
(2)作出关于x轴对称的,并写出三个顶点的坐标:(______),(______),(______);
(3)求出的面积.
18.如图,在正方形网格中,每个小正方形的边长都是1,每个小正方形的顶点叫做格点.网格中有一个格点△ABC(即三角形的顶点都在格点上).
(1)在图中画出△A1B1C1,使它与△ABC关于直线l对称;
(2)在直线l上找一点P,使得PA+PC最小;
(3)△ABC的面积为 .
19.如图,利用关于坐标轴对称的点的坐标的特点,作出ABC关于x轴对称的图形.
20.在图示的方格纸中
(1)作出△ABC关于MN对称的图形△A1B1C1;
(2)说明△A2B2C2是由△A1B1C1经过怎样的平移得到的?______________
(3)若图中每个小正方形的边长为1,则△ABC的面积是___________
21.在边长为的小正方形组成的网格中(我们把组成网格的小正方形的顶点称为格点),的三个顶点都在格点上,请利用网格线和直尺画图.
(1)在图中画出关于直线成轴对称的;
(2)求出的面积;
(3)在所给的网格内,在直线上找一点,使的面积等于的面积.
试卷第1页,共3页
试卷第1页,共3页
参考答案
1.A
解:根据关于轴对称的点,纵坐标相同,横坐标互为相反数,
点关于轴的对称点坐标为.
故选:A.
2.C
解:∵是关于x轴的对称点,
∴,
故选C.
3.A
解:点P( 3,5)关于x轴的对称点坐标为( 3, 5),
故选:A.
4.D
解:,
向右平移两个单位长度得到,
关于x轴对称的点的坐标为:.
故选:D.
5.A
解:∵点在第四象限,点在第二象限,
∴,
∴,
∴,
∴在第四象限,
∵关于x轴对称的点的坐标为
∴关于x轴对称的点在第一象限,
故选A.
6.A
解:∵A和B两点的坐标分别是(1,3)和(1,-3),
∴A和B两点的横坐标相同,纵坐标互为相反数,
∴点A和B关于x轴对称.
故选:A.
7.B
解:这是一个组合图形,它的外部是一个长方形,再根据它的组合特点,显然有2条对称轴,即两组对边的垂直平分线.
故答案选:B
8.C
解:因为点A(2,m)和点B(n,3)关于轴对称,
所以m=-3,n=2,
所以.
故选C.
9.A
解:因为点M和点N关于y轴对称,N点坐标是(5,1),
所以点M是(-5,1),
又因为点P先向左平移7个单位长度,再向上平移5个单位长度得到点M,
所以点P是(2,-4),
故选A.
10.A
解:如图,最多能画出6个格点三角形与△ABC成轴对称.
故选:A.
11.
解:点和点,点和点关于轴对称,
,,
,
故答案为:.
12.
左眼的坐标是(﹣1,0),
以两眼的中点为原点,两眼所在的直线为轴,竖直方向为轴,分别以向右和向上为正方向建立平面直角坐标系,如图,
则点即为所求,
故答案为:
13.5
解:如图所示:所标数字之处都可以构成轴对称图形.
故答案为:5.
14.1
点关于轴对称的点的坐标是,
,
解得
故答案为:
15.
解:由点关于轴的对称点为可得:,
∴将点向左平移3个单位得到点,则的坐标为;
故答案为.
16.A1(0,2)、B1(-2,0)、C1(-3,1)(答案不唯一).
解:画图如下:
∵△A1B1C1≌△ABC,
∴△A1B1C1与△ABC关y轴对称,
∵A(0,2)、B(2,0)、C(3,1),
∴A1(0,2)、B1(-2,0)、C1(-3,1)
故答案为:A1(0,2)、B1(-2,0)、C1(-3,1).
17.
(1)作出关于y轴对称的如图所示,
,,,
,,;
(2)作出关于x轴对称的如图所示,
,,,
,,;
(3)如图所示: ,
.
18.
解:(1)如图所示,△A1B1C1即为所求.
(2)连接AC1,则AC1与l的交点P即为所求的点.
(3)△ABC的面积=3×4﹣×1×4﹣×2×2﹣×2×3=5,
故答案为:5.
19.
解:如图所示,即为所求.
20.
(1)△A1B1C1如图所示;
(2)根据图形可知,△A2B2C2是由△A1B1C1向右平移6个单位,再向下平移2个单位(或向下平移2个单位,再向右平移6个单位).
故答案为:向右平移6个单位,再向下平移2个单位(或向下平移2个单位,再向右平移6个单位)
(3)
故答案为:3
21.
解:(1)如图,即为所求;
(2)连接,,
;
(3)过点B作AC的平行线交直线m于点P,则点P即为所求,如图示.
答案第1页,共2页
答案第1页,共2页
