13.3等腰三角形2021-2022学年度人教版八年级数学上册期中专题复习(Word版含解析)
文档属性
| 名称 | 13.3等腰三角形2021-2022学年度人教版八年级数学上册期中专题复习(Word版含解析) |  | |
| 格式 | docx | ||
| 文件大小 | 377.7KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-10-20 15:58:54 | ||
图片预览


文档简介
13.3等腰三角形2021-2022学年度人教版八年级数学上册期中专题复习
一、选择题
1.等腰三角形的周长为13,其中一边长为3,则该等腰三角形的底边长为( )
A.3 B.5 C.7 D.9
2.在等腰三角形ABC中,∠A=2∠B,则∠C的度数为( )
A.36° B.45° C.36°或45° D.45°或72°
3.已知等腰三角形两边的长分别为3和7,则此等腰三角形的周长为( )
A.13 B.17 C.13或17 D.13或10
4.如图,∠A=15°,AB=BC=CD=DE=EF,则∠DEF的度数为( )
A.45° B.60° C.75° D.90°
5.在等腰三角形中,AB的长是BC的2倍,周长为40,则AB的长为( )
A.20 B.16 C.16或20 D.以上都不对
6.如图,等边中,D是中点,于E,若,则长为( ).
A.6 B.4 C.2 D.1
7.如图所示,A、C、B三点在同一条直线上,△DAC和△EBC都是等边三角形,AE、BD交于点P,且分别与CD、CE交于点见M,N,有如下结论:①△ACE≌△DCB;②CM=CN;③AM=DN;④∠APD=60°,其中正确结论的个数是( )
A.4个 B.3个 C.2个 D.1个
8.和是两个全等的等边三角形,将它们按如图的方式放置在等边三角形内.若求五边形的周长,则只需知道( )
A.的周长 B.的周长 C.四边形的周长 D.的周长
9.如图,等边三角形ABC中,D、E分别在AB、BC边上,且AD=BE,AE与CD交于点F,AG⊥CD于点G.下列结论:①AE=CD;②∠AFC=120°;③△ADF是等腰三角形;④,其中正确的结论是( )
A.①② B.①③ C.①④ D.③④
10.如图,等边三角形ABC中,D、E分别为AB、BC边上的两个动点,且总使BD=CE,AE与CD交于点F,AG⊥CD于点G,则以下结论:(1)△ACE≌△CBD;(2)∠AFG=60°;(3)AF=2FG;(4)AC=2CE.其中正确的结论有( )个
A.4 B.3 C.2 D.1
二、填空题
11.已知等腰三角形的一个角是70°,则它顶角的度数为_____.
12.如图,在△ABC中,AB=AC,D为BC边上一点,∠B=30°,∠DAB=45°.则∠DAC=______°.
13.等腰三角形一边的长是4cm,周长是18cm, 则底边的长是______.
14.如图,AB=AC,AD=AE,∠BAD=20°,则∠CDE度数是_______度.
15.如图,在等边△ABC中,AB=4,P为AC的中点,M,N分别为AB,BC边上的一点,当△PMN周长取最小值时,MN长度为 ___.
16.如图,在等边△ABC中,BD=CE,将线段AE沿AC翻折得到线段AF,连结EF,CF.以下说法:①DE=EF;②∠ADB=∠AEC=∠AFC;③∠ACE=∠ACF=∠ADF④AE=DF.正确的是 ___(填序号).
三、解答题
17.如图,已知在等边△ABC中,D是AB的中点,DE⊥AC于E,EF⊥BC于F,AB=12.求BF的长.
18.用一条长为的细绳围成一个等腰三角形.
(1)如果底边长是腰长的一半,求各边长;
(2)能围成有一边长为的等腰三角形吗?如果能,请求出它的另两边.
19.已知:如图,在ABC的边BC的同侧,以AB,AC为边向外作等边三角形ABD和等边三角形ACE,连接BE、CD,相交于点M.
(1)求证:BE=CD;
(2)求∠BMC的度数.
20.如图,点O是等边△ABC内一点,D是△ABC外的一点,∠AOB=110°,∠BOC=α,△BOC≌△ADC,∠OCD=60°,连接OD.
(1)求证:△OCD是等边三角形;
(2)当α=150°时,试判断△AOD的形状,并说明理由;
(3)当α= 时,△AOD是等腰三角形.
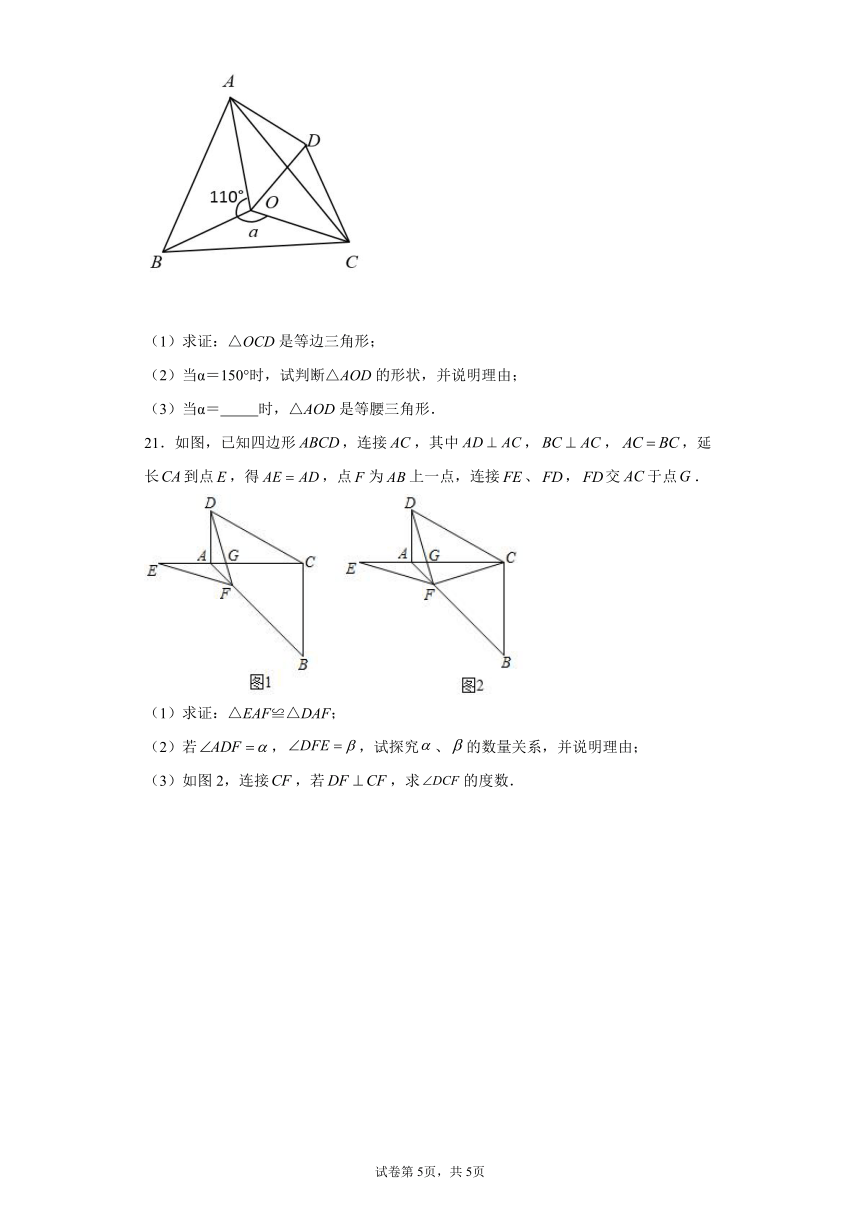
21.如图,已知四边形,连接,其中,,,延长到点,得,点为上一点,连接、,交于点.
(1)求证:△EAF≌△DAF;
(2)若,,试探究、的数量关系,并说明理由;
(3)如图2,连接,若,求的度数.
试卷第1页,共3页
试卷第1页,共3页
参考答案
1.A
解:当腰是3时,则另两边是3,7,而3+3<7,不满足三边关系定理,因而应舍去.
当底边是3时,另两边长是5,5,
则该等腰三角形的底边为3,
故选:A.
2.D
解:设∠B=x°,则∠A=2x°,
当∠A是顶角时,∠A+2∠B=180°,
即:4x=180,
解得:x=45,
此时∠C=∠B=45°;
当∠A是底角时,2∠A+∠B=180°,
即5x=180,
解得:x=36°,
此时∠C=∠A=72°,
故选:D.
3.B
解:①当腰是3,底边是7时,3+3<7不满足三角形的三边关系,因此舍去.
②当底边是3,腰长是7时,7+7>3能构成三角形,则其周长=3+7+7=17.
故选:B.
4.B
解:∵AB=BC=CD=DE=EF,∠A=15°,
∴∠BCA=∠A=15°,
∴∠CBD=∠BDC=∠BCA+∠A=15°+15°=30°,
∴,
∴,
∴,
∴,
∴∠DEF=180°﹣(∠EDF+∠EFD)=180°﹣120°=60°.
故选B.
5.B
解:①若AB为等腰三角形的腰,则BC即为底边,
由题意:AB=2BC,
∴2AB+BC=40,即:5BC=40,
解得:BC=8,
∴AB=16,
此时,等腰三角形三边为:16、16、8,满足三角形的三边关系,符合题意;
②若AB为等腰三角形的底边,则BC即为腰,
由题意:AB=2BC,
∴2BC+AB=40,即:2AB=40,
解得:AB=20,
∴BC=10,
此时,等腰三角形三边为:10、10、20,
但是10+10=20,不满足三角形的三边关系,不符合题意,舍去;
∴AB的长为16,
故选:B.
6.A
是等边三角形, D是中点,
∴AC=BC=8,∠C=60°,CD=AC=4,
,
故选A.
7.A
解:∵△DAC和△EBC都是等边三角形,
∴CA=CD,∠ACD=60°,CB=CD,∠BCE=60°,
∴∠ACE=∠DCB,
在△ACE和△DCB中,,
∴△ACE≌△DCB(SAS),所以①正确;
∴∠CAE=∠CDB,
∵∠DCN=180°﹣∠ACD﹣∠BCE=60°,
∴∠ACM=∠DCN,
在△CAM和△CDN中,,
∴△CAM≌△CDN(ASA),
∴CM=CN,AM=DN,所以②③正确;
∵∠MDP+∠DMP+∠DPM=∠MAC+∠AMC+∠ACM,
∴∠DPM=∠ACM=60°,所以④正确.
故选:A.
8.A
解:∵△GFH为等边三角形,
∴FH=GH,∠FHG=60°,
∴∠AHF+∠GHC=120°,
∵△ABC为等边三角形,
∴AB=BC=AC,∠ACB=∠A=60°,
∴∠GHC+∠HGC=120°,
∴∠AHF=∠HGC,
∴△AFH≌△CHG(AAS),
∴AF=CH.
∵△BDE和△FGH是两个全等的等边三角形,
∴BE=FH,
∴五边形DECHF的周长=DE+CE+CH+FH+DF=BD+CE+AF+BE+DF,
=(BD+DF+AF)+(CE+BE),
=AB+BC.
∴只需知道△ABC的周长即可.
故选:A.
9.A
解:在等边△ABC中,AB=AC,∠BAC=∠B=60°,
在△ABE和△CAD中,
,
∴△ABE≌△CAD(SAS),
∴AE=CD,故①正确;
∵∠ACD=∠BAE,
∴∠CAF+∠ACD=∠CAF+∠BCE=∠BAC=60°,
在△ACF中,∠AFC=180°﹣(∠CAF+∠ACD)=180°﹣60°=120°,故②正确;
∵∠FAD<∠BAC,∠BAC=∠B=60°,
∴∠ADF>60°,∠FAD<60°,∠AFD=60°,
∴△ADF不是等腰三角形,故③错误;
∵∠AFG=180°﹣∠AFC=180°﹣120°=60°,AG⊥CD,
∴∠FAG=90°﹣60°=30°,
∴FG=AF,
∴,故④错误,
综上所述,正确的有①②.
故选:A.
10.B
解:(1)∵△ABC是等边三角形,
∴AC=CB,∠ACE=∠B=60°,
在△ACE和△CBD中,
∵,
∴△ACE≌△CBD(SAS),故正确;
(2)∵△ACE≌△CBD,
∴∠CAE=∠BCD,
∴∠AFG=∠ACF+∠CAE=∠ACF+∠BCD=∠ACE=60°;故正确;
(3)∵∠AFG=60°,AG⊥CD,
∴∠FAG=30°,
∴AF=2FG;故正确;
(4)∵AC=BC,且BC不一定等于2CE,
∴AC不一定等于2CE;故错误.
故选:B.
11.40°或70°
解:当这个70度的角为顶角时,答案即为70°;
当这个70度的角为底角时,顶角=,
故答案为:40°或70°.
12.75°
解:∵AB=AC,
∴∠B=∠C=30°,
∵∠C+∠BAC+∠B=180°
∴∠BAC=180°-30°-30°=120°
∵∠DAB=45°,
∴∠DAC=∠BAC-∠DAB=120°-45°=75°
13.4cm
解:分情况考虑:
①当4cm是腰时,则底边长是18-8=10(cm),此时4,4,10不能组成三角形,应舍去;
②当4cm是底边时,腰长是(18-4)×=7(cm),
4,7,7能够组成三角形.此时底边的长是4cm.
故答案为:4cm.
14.10
解:∵AB=AC,AD=AE,
∴∠B=∠C,∠ADE=∠AED,
∵∠EDC+∠C=∠AED,
∴∠C+∠EDC=∠ADE,
又∵∠B+∠BAD=∠ADC,
∴∠B+20°=∠C+∠EDC+∠EDC,
∵∠B=∠C.
∴2∠EDC=20°,
∴∠EDC=10°.
故答案为:10.
15.2
解:作点P关于AB的对称点E,点P关于BC的对称点F,连接EF交AB于M,交BC于N,连接CE、CF,
由对称的性质可知,EM=MP,PN=NF,
∴PM+MN+PN=EM+MN+NF=EF,
∴此时△PMN的周长最小,
∵PF⊥BC,∠C=60°,
∴∠CPF=30°,
∵PE⊥AB,∠A=60°,
∴∠APE=30°,
∴∠EPF=120°,
∵P是AC的中点,
由对称性可得PE=PF,
∴∠E=∠F=30°,
∴∠EPM=∠NPF=30°,
∴∠MPN=60°,
∴△MNP是等边三角形,
∴MN=PN=PC,
∵AB=4,
∴PC=2,
∴MN=2,
故答案为2.
16.②③④
解:∵△ABC是等边三角形,
∴AB=AC,∠ABC=∠ACB=60°,
∵BD=CE,
∴△ABD≌ACE(SAS),
∴AD=AE,∠ADB=∠AEC,∠BAD=∠CAE,
由翻折的性质可知:AE=AF=AD,CE=CF,
又∵AC=AC,
∴△AEC≌△AFC(SSS),
∴∠ACF=∠ACE,∠AEC=∠AFC,∠EAC=∠FAC,
∴∠ADB=∠AEC=∠AFC,∠BAD=∠CAE=∠FAC,故②正确;
∵∠DAF=∠DAC+∠FAC=∠DAC+∠BAD=∠BAC=60°,
∴△ADF为等边三角形,
∴AF=DF=AD=AE,∠ACE=∠ACF=∠ADF=60°故④正确;
∴③正确
∵∠DAE不一定是30°,
∴∠DAE不一定等于∠FAE,
∴△ADE与△AFE不一定全等,
∴DE与EF不一定相等,故①错误;
故答案为:②③④.
17.
∵在等边△ABC中,D是AB的中点,
∴AD=BD= AB=6,
∵∠A=60°,DE⊥AE,
∴∠ADE=30°,
∴,
∴CE=AC-AE=12-3=9,
又∵∠C=60°,EF⊥BC,
∴∠FEC=30°,
∴CF=CE=,
∴BF=BC-CF=12-=.
18.(1)、、;(2)、或、.
解:(1)设底边长为,则腰长为,
由题意可得,,
解得,
,
即各边的长为、、;
(2)能围成有一边长为的等腰三角形,
当腰长为时,则底边长为,
,
能围成有腰长为的等腰三角形,
三角形的另外两边长为、;
当底边长为时,则腰长为,
,
能围成有底边长为的等腰三角形,
三角形的另外两边长为、;
由上可得,三角形的另外两边长为、或、.
19.
(1)证明: 与是等边三角形,
,,,
,
即,
在与中,
,
,
∴BE=CD;
(2)解:∵,
,
∴
,
∵是等边三角形,
∴,
∴.
20.
(1)△BOC≌△ADC,
,
∠OCD=60°,
△OCD是等边三角形;
(2)是直角三角形,理由如下:
△OCD是等边三角形;
当α=150°时,
△BOC≌△ADC
是直角三角形
(3)△OCD是等边三角形;
,
,
,
①当时,
解得
②当时,
解得
③当时
解得
综上所述,当或或时,是等腰三角形.
故答案为:或或.
21.
(1)证明:∵,,
∴,
∵,
∴,
∴,
∴,
∵,,
∴;
(2)解:,理由如下:
由(1)可得,
∴,
∵,,
∴,
∵,
∴,
∴;
(3)解:过点F作FM⊥FA交AC于点M,如图2所示:
∵,
∴△AFM是等腰直角三角形,
∴,
∴,
∴,
∵,
∴,
∴,
∴△ADF≌△MCF(ASA),
∴,
∴是等腰直角三角形,
∴.
答案第1页,共2页
答案第1页,共2页
一、选择题
1.等腰三角形的周长为13,其中一边长为3,则该等腰三角形的底边长为( )
A.3 B.5 C.7 D.9
2.在等腰三角形ABC中,∠A=2∠B,则∠C的度数为( )
A.36° B.45° C.36°或45° D.45°或72°
3.已知等腰三角形两边的长分别为3和7,则此等腰三角形的周长为( )
A.13 B.17 C.13或17 D.13或10
4.如图,∠A=15°,AB=BC=CD=DE=EF,则∠DEF的度数为( )
A.45° B.60° C.75° D.90°
5.在等腰三角形中,AB的长是BC的2倍,周长为40,则AB的长为( )
A.20 B.16 C.16或20 D.以上都不对
6.如图,等边中,D是中点,于E,若,则长为( ).
A.6 B.4 C.2 D.1
7.如图所示,A、C、B三点在同一条直线上,△DAC和△EBC都是等边三角形,AE、BD交于点P,且分别与CD、CE交于点见M,N,有如下结论:①△ACE≌△DCB;②CM=CN;③AM=DN;④∠APD=60°,其中正确结论的个数是( )
A.4个 B.3个 C.2个 D.1个
8.和是两个全等的等边三角形,将它们按如图的方式放置在等边三角形内.若求五边形的周长,则只需知道( )
A.的周长 B.的周长 C.四边形的周长 D.的周长
9.如图,等边三角形ABC中,D、E分别在AB、BC边上,且AD=BE,AE与CD交于点F,AG⊥CD于点G.下列结论:①AE=CD;②∠AFC=120°;③△ADF是等腰三角形;④,其中正确的结论是( )
A.①② B.①③ C.①④ D.③④
10.如图,等边三角形ABC中,D、E分别为AB、BC边上的两个动点,且总使BD=CE,AE与CD交于点F,AG⊥CD于点G,则以下结论:(1)△ACE≌△CBD;(2)∠AFG=60°;(3)AF=2FG;(4)AC=2CE.其中正确的结论有( )个
A.4 B.3 C.2 D.1
二、填空题
11.已知等腰三角形的一个角是70°,则它顶角的度数为_____.
12.如图,在△ABC中,AB=AC,D为BC边上一点,∠B=30°,∠DAB=45°.则∠DAC=______°.
13.等腰三角形一边的长是4cm,周长是18cm, 则底边的长是______.
14.如图,AB=AC,AD=AE,∠BAD=20°,则∠CDE度数是_______度.
15.如图,在等边△ABC中,AB=4,P为AC的中点,M,N分别为AB,BC边上的一点,当△PMN周长取最小值时,MN长度为 ___.
16.如图,在等边△ABC中,BD=CE,将线段AE沿AC翻折得到线段AF,连结EF,CF.以下说法:①DE=EF;②∠ADB=∠AEC=∠AFC;③∠ACE=∠ACF=∠ADF④AE=DF.正确的是 ___(填序号).
三、解答题
17.如图,已知在等边△ABC中,D是AB的中点,DE⊥AC于E,EF⊥BC于F,AB=12.求BF的长.
18.用一条长为的细绳围成一个等腰三角形.
(1)如果底边长是腰长的一半,求各边长;
(2)能围成有一边长为的等腰三角形吗?如果能,请求出它的另两边.
19.已知:如图,在ABC的边BC的同侧,以AB,AC为边向外作等边三角形ABD和等边三角形ACE,连接BE、CD,相交于点M.
(1)求证:BE=CD;
(2)求∠BMC的度数.
20.如图,点O是等边△ABC内一点,D是△ABC外的一点,∠AOB=110°,∠BOC=α,△BOC≌△ADC,∠OCD=60°,连接OD.
(1)求证:△OCD是等边三角形;
(2)当α=150°时,试判断△AOD的形状,并说明理由;
(3)当α= 时,△AOD是等腰三角形.
21.如图,已知四边形,连接,其中,,,延长到点,得,点为上一点,连接、,交于点.
(1)求证:△EAF≌△DAF;
(2)若,,试探究、的数量关系,并说明理由;
(3)如图2,连接,若,求的度数.
试卷第1页,共3页
试卷第1页,共3页
参考答案
1.A
解:当腰是3时,则另两边是3,7,而3+3<7,不满足三边关系定理,因而应舍去.
当底边是3时,另两边长是5,5,
则该等腰三角形的底边为3,
故选:A.
2.D
解:设∠B=x°,则∠A=2x°,
当∠A是顶角时,∠A+2∠B=180°,
即:4x=180,
解得:x=45,
此时∠C=∠B=45°;
当∠A是底角时,2∠A+∠B=180°,
即5x=180,
解得:x=36°,
此时∠C=∠A=72°,
故选:D.
3.B
解:①当腰是3,底边是7时,3+3<7不满足三角形的三边关系,因此舍去.
②当底边是3,腰长是7时,7+7>3能构成三角形,则其周长=3+7+7=17.
故选:B.
4.B
解:∵AB=BC=CD=DE=EF,∠A=15°,
∴∠BCA=∠A=15°,
∴∠CBD=∠BDC=∠BCA+∠A=15°+15°=30°,
∴,
∴,
∴,
∴,
∴∠DEF=180°﹣(∠EDF+∠EFD)=180°﹣120°=60°.
故选B.
5.B
解:①若AB为等腰三角形的腰,则BC即为底边,
由题意:AB=2BC,
∴2AB+BC=40,即:5BC=40,
解得:BC=8,
∴AB=16,
此时,等腰三角形三边为:16、16、8,满足三角形的三边关系,符合题意;
②若AB为等腰三角形的底边,则BC即为腰,
由题意:AB=2BC,
∴2BC+AB=40,即:2AB=40,
解得:AB=20,
∴BC=10,
此时,等腰三角形三边为:10、10、20,
但是10+10=20,不满足三角形的三边关系,不符合题意,舍去;
∴AB的长为16,
故选:B.
6.A
是等边三角形, D是中点,
∴AC=BC=8,∠C=60°,CD=AC=4,
,
故选A.
7.A
解:∵△DAC和△EBC都是等边三角形,
∴CA=CD,∠ACD=60°,CB=CD,∠BCE=60°,
∴∠ACE=∠DCB,
在△ACE和△DCB中,,
∴△ACE≌△DCB(SAS),所以①正确;
∴∠CAE=∠CDB,
∵∠DCN=180°﹣∠ACD﹣∠BCE=60°,
∴∠ACM=∠DCN,
在△CAM和△CDN中,,
∴△CAM≌△CDN(ASA),
∴CM=CN,AM=DN,所以②③正确;
∵∠MDP+∠DMP+∠DPM=∠MAC+∠AMC+∠ACM,
∴∠DPM=∠ACM=60°,所以④正确.
故选:A.
8.A
解:∵△GFH为等边三角形,
∴FH=GH,∠FHG=60°,
∴∠AHF+∠GHC=120°,
∵△ABC为等边三角形,
∴AB=BC=AC,∠ACB=∠A=60°,
∴∠GHC+∠HGC=120°,
∴∠AHF=∠HGC,
∴△AFH≌△CHG(AAS),
∴AF=CH.
∵△BDE和△FGH是两个全等的等边三角形,
∴BE=FH,
∴五边形DECHF的周长=DE+CE+CH+FH+DF=BD+CE+AF+BE+DF,
=(BD+DF+AF)+(CE+BE),
=AB+BC.
∴只需知道△ABC的周长即可.
故选:A.
9.A
解:在等边△ABC中,AB=AC,∠BAC=∠B=60°,
在△ABE和△CAD中,
,
∴△ABE≌△CAD(SAS),
∴AE=CD,故①正确;
∵∠ACD=∠BAE,
∴∠CAF+∠ACD=∠CAF+∠BCE=∠BAC=60°,
在△ACF中,∠AFC=180°﹣(∠CAF+∠ACD)=180°﹣60°=120°,故②正确;
∵∠FAD<∠BAC,∠BAC=∠B=60°,
∴∠ADF>60°,∠FAD<60°,∠AFD=60°,
∴△ADF不是等腰三角形,故③错误;
∵∠AFG=180°﹣∠AFC=180°﹣120°=60°,AG⊥CD,
∴∠FAG=90°﹣60°=30°,
∴FG=AF,
∴,故④错误,
综上所述,正确的有①②.
故选:A.
10.B
解:(1)∵△ABC是等边三角形,
∴AC=CB,∠ACE=∠B=60°,
在△ACE和△CBD中,
∵,
∴△ACE≌△CBD(SAS),故正确;
(2)∵△ACE≌△CBD,
∴∠CAE=∠BCD,
∴∠AFG=∠ACF+∠CAE=∠ACF+∠BCD=∠ACE=60°;故正确;
(3)∵∠AFG=60°,AG⊥CD,
∴∠FAG=30°,
∴AF=2FG;故正确;
(4)∵AC=BC,且BC不一定等于2CE,
∴AC不一定等于2CE;故错误.
故选:B.
11.40°或70°
解:当这个70度的角为顶角时,答案即为70°;
当这个70度的角为底角时,顶角=,
故答案为:40°或70°.
12.75°
解:∵AB=AC,
∴∠B=∠C=30°,
∵∠C+∠BAC+∠B=180°
∴∠BAC=180°-30°-30°=120°
∵∠DAB=45°,
∴∠DAC=∠BAC-∠DAB=120°-45°=75°
13.4cm
解:分情况考虑:
①当4cm是腰时,则底边长是18-8=10(cm),此时4,4,10不能组成三角形,应舍去;
②当4cm是底边时,腰长是(18-4)×=7(cm),
4,7,7能够组成三角形.此时底边的长是4cm.
故答案为:4cm.
14.10
解:∵AB=AC,AD=AE,
∴∠B=∠C,∠ADE=∠AED,
∵∠EDC+∠C=∠AED,
∴∠C+∠EDC=∠ADE,
又∵∠B+∠BAD=∠ADC,
∴∠B+20°=∠C+∠EDC+∠EDC,
∵∠B=∠C.
∴2∠EDC=20°,
∴∠EDC=10°.
故答案为:10.
15.2
解:作点P关于AB的对称点E,点P关于BC的对称点F,连接EF交AB于M,交BC于N,连接CE、CF,
由对称的性质可知,EM=MP,PN=NF,
∴PM+MN+PN=EM+MN+NF=EF,
∴此时△PMN的周长最小,
∵PF⊥BC,∠C=60°,
∴∠CPF=30°,
∵PE⊥AB,∠A=60°,
∴∠APE=30°,
∴∠EPF=120°,
∵P是AC的中点,
由对称性可得PE=PF,
∴∠E=∠F=30°,
∴∠EPM=∠NPF=30°,
∴∠MPN=60°,
∴△MNP是等边三角形,
∴MN=PN=PC,
∵AB=4,
∴PC=2,
∴MN=2,
故答案为2.
16.②③④
解:∵△ABC是等边三角形,
∴AB=AC,∠ABC=∠ACB=60°,
∵BD=CE,
∴△ABD≌ACE(SAS),
∴AD=AE,∠ADB=∠AEC,∠BAD=∠CAE,
由翻折的性质可知:AE=AF=AD,CE=CF,
又∵AC=AC,
∴△AEC≌△AFC(SSS),
∴∠ACF=∠ACE,∠AEC=∠AFC,∠EAC=∠FAC,
∴∠ADB=∠AEC=∠AFC,∠BAD=∠CAE=∠FAC,故②正确;
∵∠DAF=∠DAC+∠FAC=∠DAC+∠BAD=∠BAC=60°,
∴△ADF为等边三角形,
∴AF=DF=AD=AE,∠ACE=∠ACF=∠ADF=60°故④正确;
∴③正确
∵∠DAE不一定是30°,
∴∠DAE不一定等于∠FAE,
∴△ADE与△AFE不一定全等,
∴DE与EF不一定相等,故①错误;
故答案为:②③④.
17.
∵在等边△ABC中,D是AB的中点,
∴AD=BD= AB=6,
∵∠A=60°,DE⊥AE,
∴∠ADE=30°,
∴,
∴CE=AC-AE=12-3=9,
又∵∠C=60°,EF⊥BC,
∴∠FEC=30°,
∴CF=CE=,
∴BF=BC-CF=12-=.
18.(1)、、;(2)、或、.
解:(1)设底边长为,则腰长为,
由题意可得,,
解得,
,
即各边的长为、、;
(2)能围成有一边长为的等腰三角形,
当腰长为时,则底边长为,
,
能围成有腰长为的等腰三角形,
三角形的另外两边长为、;
当底边长为时,则腰长为,
,
能围成有底边长为的等腰三角形,
三角形的另外两边长为、;
由上可得,三角形的另外两边长为、或、.
19.
(1)证明: 与是等边三角形,
,,,
,
即,
在与中,
,
,
∴BE=CD;
(2)解:∵,
,
∴
,
∵是等边三角形,
∴,
∴.
20.
(1)△BOC≌△ADC,
,
∠OCD=60°,
△OCD是等边三角形;
(2)是直角三角形,理由如下:
△OCD是等边三角形;
当α=150°时,
△BOC≌△ADC
是直角三角形
(3)△OCD是等边三角形;
,
,
,
①当时,
解得
②当时,
解得
③当时
解得
综上所述,当或或时,是等腰三角形.
故答案为:或或.
21.
(1)证明:∵,,
∴,
∵,
∴,
∴,
∴,
∵,,
∴;
(2)解:,理由如下:
由(1)可得,
∴,
∵,,
∴,
∵,
∴,
∴;
(3)解:过点F作FM⊥FA交AC于点M,如图2所示:
∵,
∴△AFM是等腰直角三角形,
∴,
∴,
∴,
∵,
∴,
∴,
∴△ADF≌△MCF(ASA),
∴,
∴是等腰直角三角形,
∴.
答案第1页,共2页
答案第1页,共2页
