13.4课题学习最短路径问题2021-2022学年度人教版八年级数学上册期中专题复习(Word版含解析)
文档属性
| 名称 | 13.4课题学习最短路径问题2021-2022学年度人教版八年级数学上册期中专题复习(Word版含解析) |  | |
| 格式 | docx | ||
| 文件大小 | 736.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-10-20 16:28:23 | ||
图片预览


文档简介
13.4课题学习最短路径问题2021-2022学年度人教版八年级数学上册期中专题复习
一、选择题
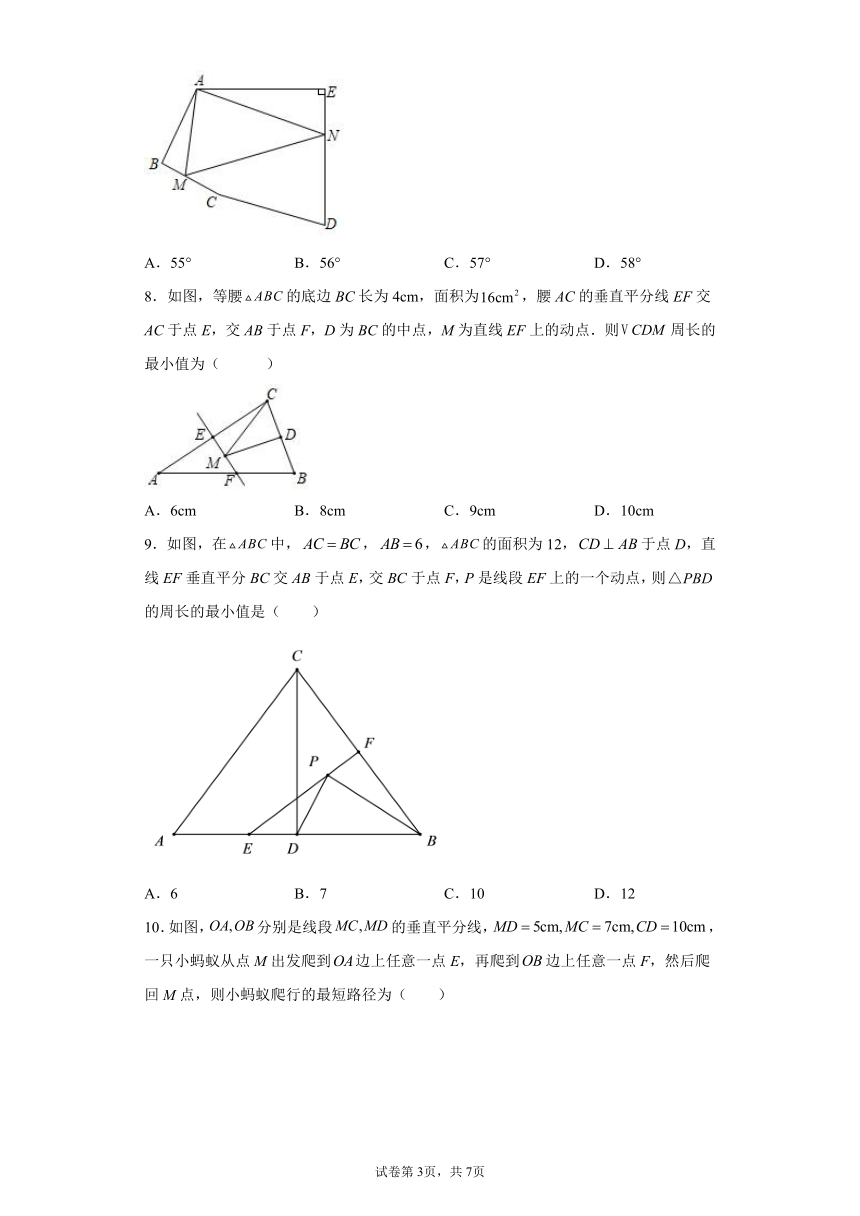
1.如图所示,直线l是一条河的河岸,P,Q是河同侧的水产的生产基地,现从河岸某点M处分别派出两辆水产车运送水产如下有四种运输方案,则运输路程合理且最短的是( )
A. B.
C. D.
2.如图,在等边三角形中,,分别是,的中点,点是线段上的一个动点,当的周长最小时,点的位置在( )
A.点处 B.点处
C.的中点处 D.三条高的交点处
3.如图,在ABC中,,,,是中点,垂直平分,交于点,交于点,在上确定一点,使最小,则这个最小值为( )
A.10 B.11 C.12 D.13
4.如图,在ABC中,,AD是其角平分线,E是边AB的中点,P是AD上一个动点,则下列线段的长度等于的最小值是( )
A.BC B.CE C.AD D.AC
5.如图,点A,B在直线l的同侧,在直线l上找一点P,使PA+PB最小,则下列图形正确的是( )
A. B.
C. D.
6.如图,在△ABC中,AB=AC,BC=4,面积是10.AB的垂直平分线ED分别交AC,AB边于E、D两点,若点F为BC边的中点,点P为线段ED上一动点,则△PBF周长的最小值为( )
A.5 B.7 C.10 D.14
7.如图,在五边形中,,,,在,上分别找一点,,使得的周长最小时,则的度数为( )
A.55° B.56° C.57° D.58°
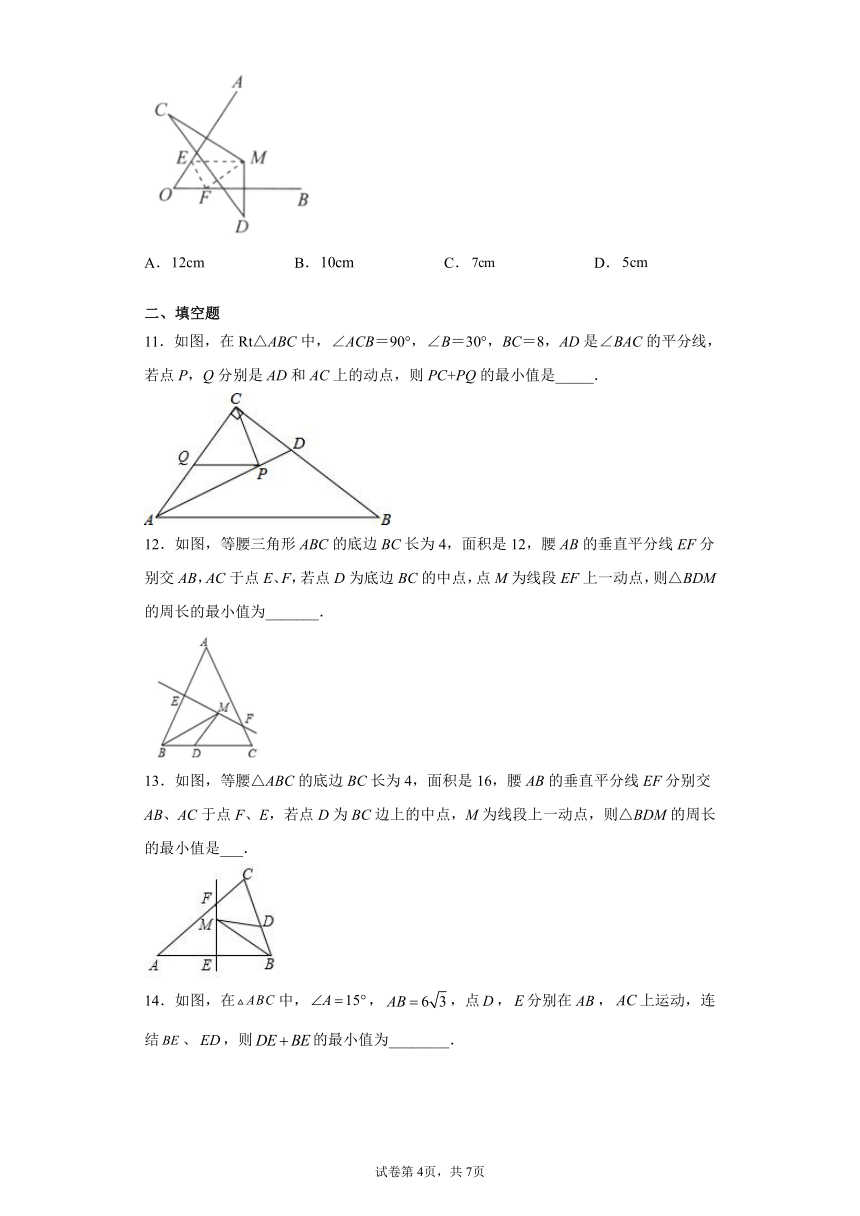
8.如图,等腰的底边BC长为4cm,面积为,腰AC的垂直平分线EF交AC于点E,交AB于点F,D为BC的中点,M为直线EF上的动点.则周长的最小值为( )
A.6cm B.8cm C.9cm D.10cm
9.如图,在中,,,的面积为12,于点D,直线EF垂直平分BC交AB于点E,交BC于点F,P是线段EF上的一个动点,则的周长的最小值是( )
A.6 B.7 C.10 D.12
10.如图,分别是线段的垂直平分线,,一只小蚂蚁从点M出发爬到边上任意一点E,再爬到边上任意一点F,然后爬回M点,则小蚂蚁爬行的最短路径为( )
A. B. C. D.
二、填空题
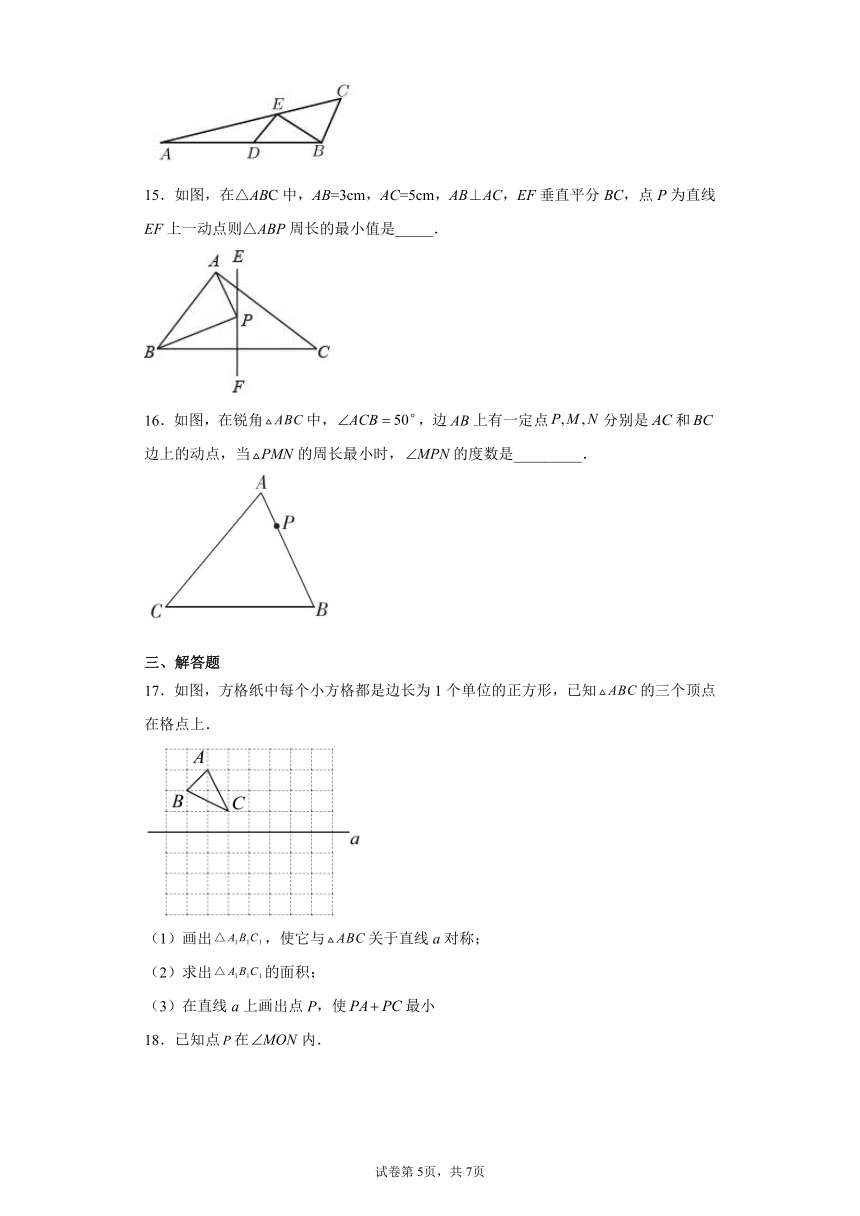
11.如图,在Rt△ABC中,∠ACB=90°,∠B=30°,BC=8,AD是∠BAC的平分线,若点P,Q分别是AD和AC上的动点,则PC+PQ的最小值是_____.
12.如图,等腰三角形ABC的底边BC长为4,面积是12,腰AB的垂直平分线EF分别交AB,AC于点E、F,若点D为底边BC的中点,点M为线段EF上一动点,则△BDM的周长的最小值为_______.
13.如图,等腰△ABC的底边BC长为4,面积是16,腰AB的垂直平分线EF分别交AB、AC于点F、E,若点D为BC边上的中点,M为线段上一动点,则△BDM的周长的最小值是___.
14.如图,在中,,,点,分别在,上运动,连结、,则的最小值为________.
15.如图,在△ABC中,AB=3cm,AC=5cm,AB⊥AC,EF垂直平分BC,点P为直线EF上一动点则△ABP周长的最小值是_____.
16.如图,在锐角中,,边上有一定点分别是和边上的动点,当的周长最小时,的度数是_________.
三、解答题
17.如图,方格纸中每个小方格都是边长为1个单位的正方形,已知的三个顶点在格点上.
(1)画出,使它与关于直线a对称;
(2)求出的面积;
(3)在直线a上画出点P,使最小
18.已知点在内.
(1)如图1,点关于射线的对称点是,点关于射线的对称点是,连接、、.
①若,则______;
②若,连接,请说明当为多少度时,;
(2)如图2,若,、分别是射线、上的任意一点,当的周长最小时,求的度数.
19.如图,等边(三边相等,三个内角都是的三角形)的边长为,动点和动点同时出发,分别以每秒的速度由向和由向运动,其中一个动点到终点时,另一个也停止运动,设运动时间为,,和交于点.
(1)在运动过程中,与始终相等吗?请说明理由;
(2)连接,求为何值时,;
(3)若于点,点为上的点,且使最短.当时,的最小值为多少?请直接写出这个最小值,无需说明理由.
20.如图,在中,已知的垂直平分线交于点N,交于点M,连接.
(1)若,求的度数.
(2)若,的周长是.
①求的长度;
②若点P为直线上一点,请你求出周长的最小值.
试卷第1页,共3页
试卷第1页,共3页
参考答案
1.B
根据“将军饮马”模型求最短路线题型,作点P关于直线l的对称点,连接Q交直线l于点M,利用两点之间线段最短和线段垂直平分线的性质作图即可,
故选:B.
2.D
解:连接BP,
∵△ABC是等边三角形,D是BC的中点,
∴AD是BC的垂直平分线,
∴PB=PC,
当PC+PE的长最小时,即PB+PE最小
则此时点B、P、E在同一直线上,
又∵BE为中线,△ABC是等边三角形
∴点P为△ABC的三条中线的交点,也就是△ABC的三条高的交点.
故选:D
3.C
∵AB=AC,BC=10,S△ABC=60,是中点,
AD⊥BC于点D,
∴S△ABC= =60,
∴AD=12,
设AD与EF的交点为P,
∵EF垂直平分AB,
∴点A,B关于直线EF对称,
∴PA=PB,
此时AD的长为PB+PD的最小值,
即PB+PD的最小值为12,
故选:C.
4.B
解:如图,连接PC,
∵,AD是其角平分线,
∴AD⊥BC,BD=CD,
∴PB=PC,
∴PB+PE=PC+PE,
∵PC+PE≥CE,
∴P、C、E共线时,PB+PE的值最小,最小值为CE的长度.
故选B.
5.B
解:∵点A,B在直线l的同侧,
∴作A点关于l的对称点A',连接A'B与l的交点为P,
由对称性可知AP=A'P,
此时PA+PB最小,
故选:B.
6.B
解:如图,连接AF,AP.
∵AC=AB,CF=BF=BC=2,
∴AF⊥BC,
∵S△ABC= BC AF=10,BC=4,
∴AF=5,
∵DE垂直平分线段AB,
∴PA=PB,
∴△PBF的周长=PB+PF+BF=PA+PF+2,
∵PA+PF≥AF,
∴PA+PF的最小值为5,
∴△PBF的周长的最小值为7.
故选:B.
7.B
解:作A关于BC的对称点G,A关于DE的对称点H,连接MG,NH,
则AM=MG,AN=NH,
∴△AMN的周长为AM+MN+AN=MG+MN+NH,
由两点之间,线段最短可知:当G、M、N、H共线时,△AMN的周长最小,
∵∠BAE=152°,
∴∠G+∠H=28°,
∵AM=MG,AN=NH,
∴∠G=∠GAM,∠H=∠HAN,
∠AMN+∠ANM=2∠G+2∠H=2×28°=56°,
故选:B.
8.D
解:连接AD,MA.
∵△ABC是等腰三角形,点D是BC边的中点,
∴AD⊥BC,
∴S△ABC=BC AD=×4×AD=16,解得AD=8 cm,
∵EF是线段AC的垂直平分线,
∴MA=MC,
∴MC+DM=MA+DM≥AD,
∴AD的长为CM+MD的最小值,
∴△CDM的周长最短=(CM+MD)+CD=AD+BC=8+×4=10(cm).
故选:D.
9.B
如图
∵的面积为12,
∴,,
解得,,
∵直线EF垂直平分BC交AB于点E,
∴点和点关于直线EF对称,
∴当与重合时,的值最小,最小值等于的长,
∴周长的最小值是,
故选:B.
10.B
由题意可知与的交点为E,与的交点为F.
∵分别是线段的垂直平分线,
∴,
∴小蚂蚁爬行的最短路径为.
11.4
解:如图,过C作CM⊥AB,交AD于P,交AB于M,过P作PQ⊥AC于Q,
∵AD是∠BAC的平分线,
∴PQ=PM,
这时PC+PQ有最小值,即CM的长度,
∵CM⊥AB,∠B=30°,BC=8,
∴CM==4,
∴PC+PQ的最小值为4.
故答案为:4.
12.8
解:连接AD交EF与点M′,连接AM.
∵△ABC是等腰三角形,点D是BC边的中点,
∴AD⊥BC,
∴S△ABC=BC AD=×4×AD=12,解得AD=6,
∵EF是线段AB的垂直平分线,
∴AM=BM.
∴BM+MD=MD+AM.
∴当点M位于点M′处时,MB+MD有最小值,最小值6.
∴△BDM的周长的最小值为DB+AD=2+6=8,
故答案为:8.
13.10
解:如图,连接AD.
∵△ABC是等腰三角形,点D是BC边的中点,
∴AD⊥BC,
∴S△ABC= BC AD=×4×AD=16.
∴AD=8.
∵EF是线段AB的垂直平分线,
∴点B关于直线EF的对称点为点A,
∴AD的长为BM+MD的最小值,
∴△BDM的周长最短=(BM+MD)+BD=AD+BC=6+×8=10.
故答案为:10.
14.
解:作B关于AC的对称点B′,过B′作B′D⊥AB交AC于E,连接AB′,
此时B′E+ED=BE+ED为最小值,
此时∠B′AB=2∠BAC=30°,B′D=AB′=AB=,
即BE+ED的最小值为,
故答案为:.
15.8cm
如图,连接PC,
∵AB=3 cm
∴△ABP的周长为AB+PA+PB=3+PA+PB,
要使△ABP的周长最小,则需PA+PB的值最小,
∵EF垂直平分BC,
∴PC=PB,
∴PA+PB=PA+PC,
由两点之间线段最短可知,当点A,P,C共线,
即点P在AC边上时,PA+PC取得最小值,最小值为AC,
即PA+PB的最小值为AC=5 cm,
则△ABP周长的最小值是3+5=8 cm,
故答案为:8.
16.80°
∵ PD⊥AC,PG⊥BC,
∴∠PEC=∠PFC=90°,
∴ ∠C+∠EPF=180°,
∵∠C=50°,
∵∠D+∠G+∠EPF=180°,
∴ ∠D+∠G=50°,
由对称可知:∠G=∠GPN,∠D=∠DPM, L
∴∠GPN+∠DPM=50°,
∴∠MPN=130°-50°=80°,
故答案为:80°.
17.(1)如图,△A1B1C1即为所求.
(2)=2×2-×1×2×2-×1×1=.
(3)如图,连接C1A(或A1C)与直线a交于点P,则点P即为所求.
18.
(1)①∵点P关于射线OM的对称点是G,点P关于射线ON的对称点是H,
∴OG=OP,OM⊥GP,
∴OM平分∠POG,
同理可得ON平分∠POH,
∴∠GOH=2∠MON=2×50°=100°,
故答案为:100°;
②,,
、、三点其线,
,
,
当时,;
(2)如图所示:分别作点关于、的对称点、,
连接,、、,交、于点、,
则,,
此时周长的最小值等于的长.
由轴对称性质可得,,
,
,
,
,
由轴对称性质可得,
.
19.
解:(1)由已知可得AD=t,EC=t,
∴AD=CE,
∵△ABC是等边三角形
∴∠A=∠ACB=60°,BC=AC,
∴△ADC≌△CEB(SAS),
∴BE=CD,
∴CD与BE始终相等;
(2)∵DE∥BC,
∴AD=AE,
∵AB=AC=10,
∴t=10-t,
∴t=5;
(3)∵BM⊥AC,
∴BM平分∠ABC,
作D点关于BM的对称点D'交BC于点D',连接D'E,交BM于点P,
∵DP=D'P,
∴DP+PE=D'P+PE=D'E,
∵t=7,
∴AE=BD=BD′=3,AD=CE=7,
∴CD′=7,又∠C=60°,
∴△CD′E为等边三角形,
∴D'E=CD′=7,
∴PD+PE的最小值为7.
20.
解:(1)∵,
∴,
∴,
∵的垂直平分线交于点N,
∴,
∴;
(2)①∵是的垂直平分线,
∴,
∴的周长,
∵,的周长是,
∴;
②周长最小,即最小,
根据轴对称性质得,当点P与M重合时,即最小,
此时 周长的值最小,
∴周长的最小值.
答案第1页,共2页
答案第1页,共2页
一、选择题
1.如图所示,直线l是一条河的河岸,P,Q是河同侧的水产的生产基地,现从河岸某点M处分别派出两辆水产车运送水产如下有四种运输方案,则运输路程合理且最短的是( )
A. B.
C. D.
2.如图,在等边三角形中,,分别是,的中点,点是线段上的一个动点,当的周长最小时,点的位置在( )
A.点处 B.点处
C.的中点处 D.三条高的交点处
3.如图,在ABC中,,,,是中点,垂直平分,交于点,交于点,在上确定一点,使最小,则这个最小值为( )
A.10 B.11 C.12 D.13
4.如图,在ABC中,,AD是其角平分线,E是边AB的中点,P是AD上一个动点,则下列线段的长度等于的最小值是( )
A.BC B.CE C.AD D.AC
5.如图,点A,B在直线l的同侧,在直线l上找一点P,使PA+PB最小,则下列图形正确的是( )
A. B.
C. D.
6.如图,在△ABC中,AB=AC,BC=4,面积是10.AB的垂直平分线ED分别交AC,AB边于E、D两点,若点F为BC边的中点,点P为线段ED上一动点,则△PBF周长的最小值为( )
A.5 B.7 C.10 D.14
7.如图,在五边形中,,,,在,上分别找一点,,使得的周长最小时,则的度数为( )
A.55° B.56° C.57° D.58°
8.如图,等腰的底边BC长为4cm,面积为,腰AC的垂直平分线EF交AC于点E,交AB于点F,D为BC的中点,M为直线EF上的动点.则周长的最小值为( )
A.6cm B.8cm C.9cm D.10cm
9.如图,在中,,,的面积为12,于点D,直线EF垂直平分BC交AB于点E,交BC于点F,P是线段EF上的一个动点,则的周长的最小值是( )
A.6 B.7 C.10 D.12
10.如图,分别是线段的垂直平分线,,一只小蚂蚁从点M出发爬到边上任意一点E,再爬到边上任意一点F,然后爬回M点,则小蚂蚁爬行的最短路径为( )
A. B. C. D.
二、填空题
11.如图,在Rt△ABC中,∠ACB=90°,∠B=30°,BC=8,AD是∠BAC的平分线,若点P,Q分别是AD和AC上的动点,则PC+PQ的最小值是_____.
12.如图,等腰三角形ABC的底边BC长为4,面积是12,腰AB的垂直平分线EF分别交AB,AC于点E、F,若点D为底边BC的中点,点M为线段EF上一动点,则△BDM的周长的最小值为_______.
13.如图,等腰△ABC的底边BC长为4,面积是16,腰AB的垂直平分线EF分别交AB、AC于点F、E,若点D为BC边上的中点,M为线段上一动点,则△BDM的周长的最小值是___.
14.如图,在中,,,点,分别在,上运动,连结、,则的最小值为________.
15.如图,在△ABC中,AB=3cm,AC=5cm,AB⊥AC,EF垂直平分BC,点P为直线EF上一动点则△ABP周长的最小值是_____.
16.如图,在锐角中,,边上有一定点分别是和边上的动点,当的周长最小时,的度数是_________.
三、解答题
17.如图,方格纸中每个小方格都是边长为1个单位的正方形,已知的三个顶点在格点上.
(1)画出,使它与关于直线a对称;
(2)求出的面积;
(3)在直线a上画出点P,使最小
18.已知点在内.
(1)如图1,点关于射线的对称点是,点关于射线的对称点是,连接、、.
①若,则______;
②若,连接,请说明当为多少度时,;
(2)如图2,若,、分别是射线、上的任意一点,当的周长最小时,求的度数.
19.如图,等边(三边相等,三个内角都是的三角形)的边长为,动点和动点同时出发,分别以每秒的速度由向和由向运动,其中一个动点到终点时,另一个也停止运动,设运动时间为,,和交于点.
(1)在运动过程中,与始终相等吗?请说明理由;
(2)连接,求为何值时,;
(3)若于点,点为上的点,且使最短.当时,的最小值为多少?请直接写出这个最小值,无需说明理由.
20.如图,在中,已知的垂直平分线交于点N,交于点M,连接.
(1)若,求的度数.
(2)若,的周长是.
①求的长度;
②若点P为直线上一点,请你求出周长的最小值.
试卷第1页,共3页
试卷第1页,共3页
参考答案
1.B
根据“将军饮马”模型求最短路线题型,作点P关于直线l的对称点,连接Q交直线l于点M,利用两点之间线段最短和线段垂直平分线的性质作图即可,
故选:B.
2.D
解:连接BP,
∵△ABC是等边三角形,D是BC的中点,
∴AD是BC的垂直平分线,
∴PB=PC,
当PC+PE的长最小时,即PB+PE最小
则此时点B、P、E在同一直线上,
又∵BE为中线,△ABC是等边三角形
∴点P为△ABC的三条中线的交点,也就是△ABC的三条高的交点.
故选:D
3.C
∵AB=AC,BC=10,S△ABC=60,是中点,
AD⊥BC于点D,
∴S△ABC= =60,
∴AD=12,
设AD与EF的交点为P,
∵EF垂直平分AB,
∴点A,B关于直线EF对称,
∴PA=PB,
此时AD的长为PB+PD的最小值,
即PB+PD的最小值为12,
故选:C.
4.B
解:如图,连接PC,
∵,AD是其角平分线,
∴AD⊥BC,BD=CD,
∴PB=PC,
∴PB+PE=PC+PE,
∵PC+PE≥CE,
∴P、C、E共线时,PB+PE的值最小,最小值为CE的长度.
故选B.
5.B
解:∵点A,B在直线l的同侧,
∴作A点关于l的对称点A',连接A'B与l的交点为P,
由对称性可知AP=A'P,
此时PA+PB最小,
故选:B.
6.B
解:如图,连接AF,AP.
∵AC=AB,CF=BF=BC=2,
∴AF⊥BC,
∵S△ABC= BC AF=10,BC=4,
∴AF=5,
∵DE垂直平分线段AB,
∴PA=PB,
∴△PBF的周长=PB+PF+BF=PA+PF+2,
∵PA+PF≥AF,
∴PA+PF的最小值为5,
∴△PBF的周长的最小值为7.
故选:B.
7.B
解:作A关于BC的对称点G,A关于DE的对称点H,连接MG,NH,
则AM=MG,AN=NH,
∴△AMN的周长为AM+MN+AN=MG+MN+NH,
由两点之间,线段最短可知:当G、M、N、H共线时,△AMN的周长最小,
∵∠BAE=152°,
∴∠G+∠H=28°,
∵AM=MG,AN=NH,
∴∠G=∠GAM,∠H=∠HAN,
∠AMN+∠ANM=2∠G+2∠H=2×28°=56°,
故选:B.
8.D
解:连接AD,MA.
∵△ABC是等腰三角形,点D是BC边的中点,
∴AD⊥BC,
∴S△ABC=BC AD=×4×AD=16,解得AD=8 cm,
∵EF是线段AC的垂直平分线,
∴MA=MC,
∴MC+DM=MA+DM≥AD,
∴AD的长为CM+MD的最小值,
∴△CDM的周长最短=(CM+MD)+CD=AD+BC=8+×4=10(cm).
故选:D.
9.B
如图
∵的面积为12,
∴,,
解得,,
∵直线EF垂直平分BC交AB于点E,
∴点和点关于直线EF对称,
∴当与重合时,的值最小,最小值等于的长,
∴周长的最小值是,
故选:B.
10.B
由题意可知与的交点为E,与的交点为F.
∵分别是线段的垂直平分线,
∴,
∴小蚂蚁爬行的最短路径为.
11.4
解:如图,过C作CM⊥AB,交AD于P,交AB于M,过P作PQ⊥AC于Q,
∵AD是∠BAC的平分线,
∴PQ=PM,
这时PC+PQ有最小值,即CM的长度,
∵CM⊥AB,∠B=30°,BC=8,
∴CM==4,
∴PC+PQ的最小值为4.
故答案为:4.
12.8
解:连接AD交EF与点M′,连接AM.
∵△ABC是等腰三角形,点D是BC边的中点,
∴AD⊥BC,
∴S△ABC=BC AD=×4×AD=12,解得AD=6,
∵EF是线段AB的垂直平分线,
∴AM=BM.
∴BM+MD=MD+AM.
∴当点M位于点M′处时,MB+MD有最小值,最小值6.
∴△BDM的周长的最小值为DB+AD=2+6=8,
故答案为:8.
13.10
解:如图,连接AD.
∵△ABC是等腰三角形,点D是BC边的中点,
∴AD⊥BC,
∴S△ABC= BC AD=×4×AD=16.
∴AD=8.
∵EF是线段AB的垂直平分线,
∴点B关于直线EF的对称点为点A,
∴AD的长为BM+MD的最小值,
∴△BDM的周长最短=(BM+MD)+BD=AD+BC=6+×8=10.
故答案为:10.
14.
解:作B关于AC的对称点B′,过B′作B′D⊥AB交AC于E,连接AB′,
此时B′E+ED=BE+ED为最小值,
此时∠B′AB=2∠BAC=30°,B′D=AB′=AB=,
即BE+ED的最小值为,
故答案为:.
15.8cm
如图,连接PC,
∵AB=3 cm
∴△ABP的周长为AB+PA+PB=3+PA+PB,
要使△ABP的周长最小,则需PA+PB的值最小,
∵EF垂直平分BC,
∴PC=PB,
∴PA+PB=PA+PC,
由两点之间线段最短可知,当点A,P,C共线,
即点P在AC边上时,PA+PC取得最小值,最小值为AC,
即PA+PB的最小值为AC=5 cm,
则△ABP周长的最小值是3+5=8 cm,
故答案为:8.
16.80°
∵ PD⊥AC,PG⊥BC,
∴∠PEC=∠PFC=90°,
∴ ∠C+∠EPF=180°,
∵∠C=50°,
∵∠D+∠G+∠EPF=180°,
∴ ∠D+∠G=50°,
由对称可知:∠G=∠GPN,∠D=∠DPM, L
∴∠GPN+∠DPM=50°,
∴∠MPN=130°-50°=80°,
故答案为:80°.
17.(1)如图,△A1B1C1即为所求.
(2)=2×2-×1×2×2-×1×1=.
(3)如图,连接C1A(或A1C)与直线a交于点P,则点P即为所求.
18.
(1)①∵点P关于射线OM的对称点是G,点P关于射线ON的对称点是H,
∴OG=OP,OM⊥GP,
∴OM平分∠POG,
同理可得ON平分∠POH,
∴∠GOH=2∠MON=2×50°=100°,
故答案为:100°;
②,,
、、三点其线,
,
,
当时,;
(2)如图所示:分别作点关于、的对称点、,
连接,、、,交、于点、,
则,,
此时周长的最小值等于的长.
由轴对称性质可得,,
,
,
,
,
由轴对称性质可得,
.
19.
解:(1)由已知可得AD=t,EC=t,
∴AD=CE,
∵△ABC是等边三角形
∴∠A=∠ACB=60°,BC=AC,
∴△ADC≌△CEB(SAS),
∴BE=CD,
∴CD与BE始终相等;
(2)∵DE∥BC,
∴AD=AE,
∵AB=AC=10,
∴t=10-t,
∴t=5;
(3)∵BM⊥AC,
∴BM平分∠ABC,
作D点关于BM的对称点D'交BC于点D',连接D'E,交BM于点P,
∵DP=D'P,
∴DP+PE=D'P+PE=D'E,
∵t=7,
∴AE=BD=BD′=3,AD=CE=7,
∴CD′=7,又∠C=60°,
∴△CD′E为等边三角形,
∴D'E=CD′=7,
∴PD+PE的最小值为7.
20.
解:(1)∵,
∴,
∴,
∵的垂直平分线交于点N,
∴,
∴;
(2)①∵是的垂直平分线,
∴,
∴的周长,
∵,的周长是,
∴;
②周长最小,即最小,
根据轴对称性质得,当点P与M重合时,即最小,
此时 周长的值最小,
∴周长的最小值.
答案第1页,共2页
答案第1页,共2页
