人教版数学四年级下册解决两步数学问题教案
文档属性
| 名称 | 人教版数学四年级下册解决两步数学问题教案 |  | |
| 格式 | docx | ||
| 文件大小 | 174.8KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-10-21 06:10:51 | ||
图片预览


文档简介
《解决两步数学问题》教学设计
教学内容
四年级下册解决两步数学问题。
教材分析:
学生学了四年级上册除数是两位数的除法后,小学阶段的整数乘除法就告一段落,也就是说整数四则运算基本结束。紧接着要运用四则运算的数学知识解决生活中的数学问题。
小学阶段,解决数学问题是数学教学的难点。新课标规定,义务教育小学阶段数学问题的步骤基本上以两步为主,最多不超过三步。从数学问题的步骤内在联系来看,两步数学问题是“问题解决”教学的关键。学好它将对学生今后到高学段学习更为复杂的应数学问题打下坚实的基础。同时对学生掌握数学问题的基本解题思路做好铺垫。因此,教师必须重视这部分知识的教学。
学情分析:
学生经过近四年的数学学习,小学阶段最基本的4类数量关系,11个最基本的数学问题他们都以接触完毕。多数学生都能解决步骤简单的数学问题。这时他们的抽象逻辑思维能力也得到了一定的发展。
此时,教师可以尝试放点手引导学生解决较为复杂的数学问题,使部分学生的数学思维得到更快、更高的发展。这对学生的创新意识与数学应用意识的培养不妨也是一个很好的路径。
设计理念
当今社会需要的是哪些具有创新精神与勇于开拓性的适用型人才。这就要求我们的教育,要特别重视学生创新能力的培养。创新能力的人都具有思维奇特,想想力丰富的特质。根据数学学科思维性强的特点,数学课堂教学更应该把培养学生的思维品质放在第一位。在此基础上,进一步重视培养他们的自学能力。为学生终身独立学习做好一定的铺垫。
教学目标
1.了解两步复合数学问题的基本结构,掌握两步复合数学问题的一般解题思路。
2.找准解决两步复合数学问题的思维源头,培养学生思维的逻辑性与条理性。
3.做到思考数学问题时,思维有序,源头有向。
4.形成完善的两步复合数学问题的知识体系,基本具备举一反三、触类旁通的能力。培养学生的创新意识与应用意识。
教学重点:掌握两步复合数学问题的基本结构,与解题的一般步骤。
教学难点:找准两步数学问题的思维源头。
教学过程
一、数量关系小盘点
卡片出示下列复习内容:
1.下列数量关系分别是哪种类型?与什么计算方法有关?说说你是怎么理解这些语句的?
(1)皮鞋总数、男式皮鞋数量、女士皮鞋数量。
(2)英语期中成绩比数学成绩还多5分。
(3)一枝毛笔书法笔的价格是普通钢笔单价的5倍。
(4)早操时学生站队总人数,每行人数、站队行数。
2.引入新课,板书课题:解决两步数学问题。
(设计意图:通过学生对数量关系类型知识的小回顾,了解学生对数量关系知识的掌握情况,便于教师在下一环节中有针对性的从教学)
二、新授教学
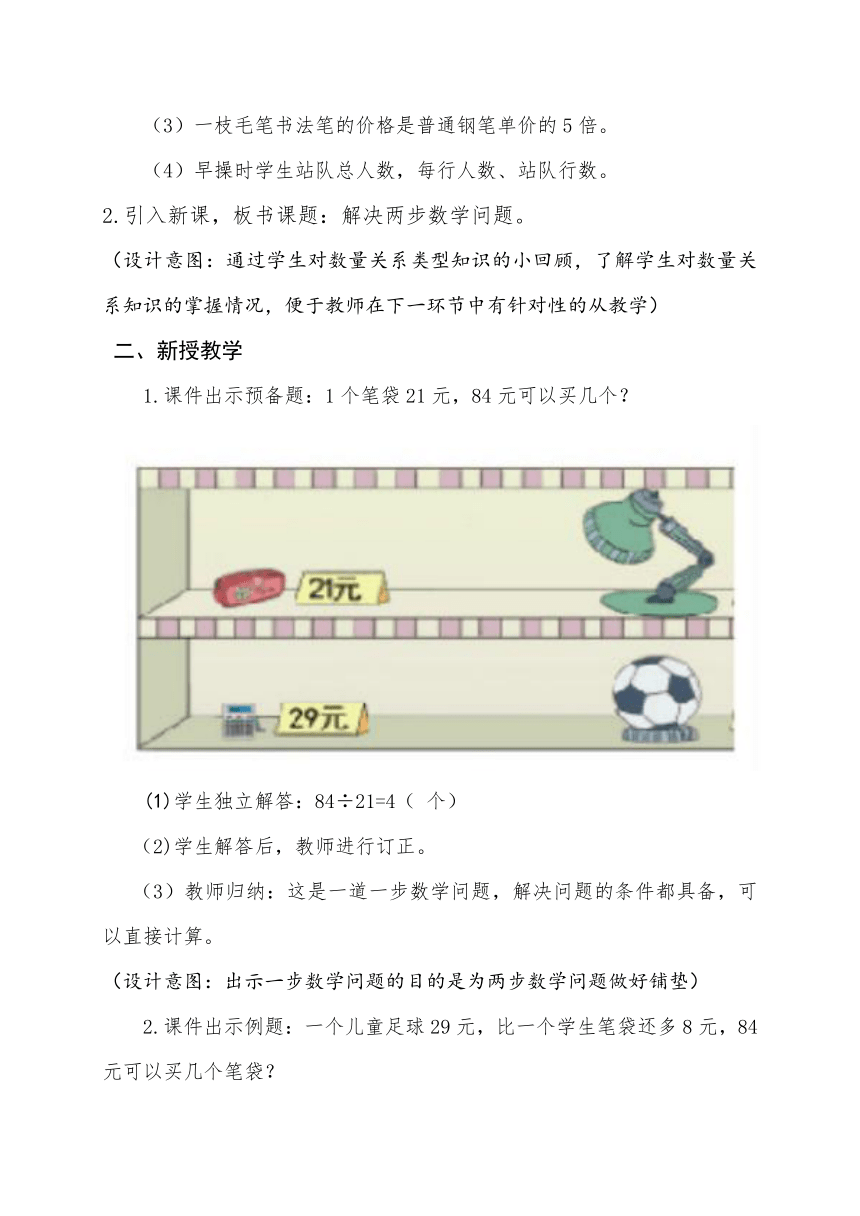
1.课件出示预备题:1个笔袋21元,84元可以买几个?
(1)学生独立解答:84÷21=4( 个)
(2)学生解答后,教师进行订正。
(3)教师归纳:这是一道一步数学问题,解决问题的条件都具备,可以直接计算。
(设计意图:出示一步数学问题的目的是为两步数学问题做好铺垫)
2.课件出示例题:一个儿童足球29元,比一个学生笔袋还多8元,84元可以买几个笔袋?
(一)自学提示:
(1)例题与预备题有何异同?
(2)同一个数学问题,哪道题易做,哪道题还不能直接做出来?为什么
(3)解答例题中的数学问题还需要什么条件?
(4) 交流讨论,教师对个别学困生点拨辅导。
(5)学生代表发言,教师补充。
板书:问题一:一个学生笔袋多少元?问题二:需要多少个笔袋?
29-8=21元 84÷21=4(个)
(二)教师精讲小结。
预备题与例题的数学问题一样,但解答的步骤不一样,预备题是一道一步直接计算的数学问题,例题是两步计算的复合数学问题,不能直接计算,要把隐含问题找出来并解答,然后做为解决最后问题其中的一个条件,并与例题中的另一个条件结合起来,最后再解决最后的数学问题。
板书、 一步单一问题 两步复合问题
直接计算 解答隐含问题
(设计意图:从同一个数学问题入手,由一步数学问题铺垫到第二个问题,便于学生理解两者的不同,初步理解两步数学问题的基本结构。)
迁移反馈练习
1.晨光小学有男生300人,女学生312人,每18人组成一个环保小组,能组成多少个小组?
2.红旗小学有学生645人,比晨光小学还多33人,每18人组成一个环保小组,晨光小学能组成多少个环保小组?
3.红旗小学有学生584人,晨光小学比红旗小学还多28人,每18人组成一个环保小组,晨光能组成多少个环保小组?
(1)学习提示:
(这几个数学问题是一步问题还是两步问题?能直接解答吗?)
(要求能组成多少个小组还需要哪一个条件?)
(2)学生自己独立解答,教师巡视指导学困生。
(3)学生代表发言,教师纠正点拨。
(设计意图:出示同样的数学问题,但题目中的隐含问题不同,隐含问题的解决要用到不同的数量关系,便于构建两部数学问题的知识体系,通过一道题的解答,可使学生进行学法的迁移,有利于培养学生的自学能力)
四、课中交流,深化学习
同学们,通过本节课的学习,你能总结两部数学问题的解题思路吗,他们在结构上有何特点?
(设计意图:师生之间,学生与学生之间相互交流,总结两步数学问题的解题思路,与两步数学问题结构特点,对学生学习方法的迁移以及自学能力的培养起到潜移默化的作用)。
五、作业。
1.一箱蜜蜂平均一年可以酿造蜂蜜75千克千克,爷爷养了3箱,爸爸养了9箱,每年总共可以酿造多少蜂蜜?
2.一箱蜜蜂平均一年可以酿造蜂蜜75千克千克,爷爷养了3箱这样的蜜蜂,爸爸养蜂的数量是爷爷数量的3倍,爸爸每年可以收多少千克的蜂蜜?
3.一箱蜜蜂平均一年可以酿造蜂蜜75千克千克,爸爸养了9箱这样的蜂蜜,是爷爷养蜂数量的3倍,爷爷每年可以收多少千克的蜂蜜?
4.一箱蜜蜂平均一年可以酿造蜂蜜75千克千克,爸爸养了17箱这样的蜂蜜,当年卖掉了11箱蜂蜜,余下的蜂蜜有多少千克?
5一箱蜜蜂平均一年可以酿造蜂蜜75千克千克,爷爷养了3箱,比爸爸少5箱,爸爸每年可以收多少千克的蜂蜜?
6.一箱蜜蜂平均一年可以酿造蜂蜜75千克千克,爸爸在养蜂房里搭了一个蜜箱架,共3层,每层放5个蜂箱,爸爸一年可以收多少千克的蜂蜜?
(设计意图:6个数学问题中,每个题中的隐含问题都是11个最基本的数学问题中的一种,也涉及到小学阶段最基础的4类数量关系。这样做,便于学生更加熟练地掌握四种数量关系,而且隐含问题是不同种类的数学问题,要用到加、减、乘、除四种运算方法。这样自然而然就构建起了两步数学问题的知识体系,对于学生学法的迁移,能力的培养都起到积极作用)
板书设计 解决两步数学问题
1.课件出示预备题:1个 笔袋 2.出示例题:一个儿童足球 29元,
21元,84元可以买几个? 比一个学生笔袋还多8元,84元可
以买几个?
一步数学问题 两步数学问题 不
条 1个 笔袋 21元 直 隐含问题: 一个学生笔袋多少元?能
接 29-8=21(元) 直
件 84元 算 问题二: 简介条件 29元 8元 接
直接条件 84元 算
84÷21=4(元) 84 ÷ 21 = 4(个)
84 ÷(29—8)= 4(个)
答:可以买4个笔袋。
(设计意图:板书本节知识的纲要符号,提炼精华内容便于学生掌握知识重点与要点,更加便于学生掌握两步复合数学问题的基本结构与解题思路)。
教学内容
四年级下册解决两步数学问题。
教材分析:
学生学了四年级上册除数是两位数的除法后,小学阶段的整数乘除法就告一段落,也就是说整数四则运算基本结束。紧接着要运用四则运算的数学知识解决生活中的数学问题。
小学阶段,解决数学问题是数学教学的难点。新课标规定,义务教育小学阶段数学问题的步骤基本上以两步为主,最多不超过三步。从数学问题的步骤内在联系来看,两步数学问题是“问题解决”教学的关键。学好它将对学生今后到高学段学习更为复杂的应数学问题打下坚实的基础。同时对学生掌握数学问题的基本解题思路做好铺垫。因此,教师必须重视这部分知识的教学。
学情分析:
学生经过近四年的数学学习,小学阶段最基本的4类数量关系,11个最基本的数学问题他们都以接触完毕。多数学生都能解决步骤简单的数学问题。这时他们的抽象逻辑思维能力也得到了一定的发展。
此时,教师可以尝试放点手引导学生解决较为复杂的数学问题,使部分学生的数学思维得到更快、更高的发展。这对学生的创新意识与数学应用意识的培养不妨也是一个很好的路径。
设计理念
当今社会需要的是哪些具有创新精神与勇于开拓性的适用型人才。这就要求我们的教育,要特别重视学生创新能力的培养。创新能力的人都具有思维奇特,想想力丰富的特质。根据数学学科思维性强的特点,数学课堂教学更应该把培养学生的思维品质放在第一位。在此基础上,进一步重视培养他们的自学能力。为学生终身独立学习做好一定的铺垫。
教学目标
1.了解两步复合数学问题的基本结构,掌握两步复合数学问题的一般解题思路。
2.找准解决两步复合数学问题的思维源头,培养学生思维的逻辑性与条理性。
3.做到思考数学问题时,思维有序,源头有向。
4.形成完善的两步复合数学问题的知识体系,基本具备举一反三、触类旁通的能力。培养学生的创新意识与应用意识。
教学重点:掌握两步复合数学问题的基本结构,与解题的一般步骤。
教学难点:找准两步数学问题的思维源头。
教学过程
一、数量关系小盘点
卡片出示下列复习内容:
1.下列数量关系分别是哪种类型?与什么计算方法有关?说说你是怎么理解这些语句的?
(1)皮鞋总数、男式皮鞋数量、女士皮鞋数量。
(2)英语期中成绩比数学成绩还多5分。
(3)一枝毛笔书法笔的价格是普通钢笔单价的5倍。
(4)早操时学生站队总人数,每行人数、站队行数。
2.引入新课,板书课题:解决两步数学问题。
(设计意图:通过学生对数量关系类型知识的小回顾,了解学生对数量关系知识的掌握情况,便于教师在下一环节中有针对性的从教学)
二、新授教学
1.课件出示预备题:1个笔袋21元,84元可以买几个?
(1)学生独立解答:84÷21=4( 个)
(2)学生解答后,教师进行订正。
(3)教师归纳:这是一道一步数学问题,解决问题的条件都具备,可以直接计算。
(设计意图:出示一步数学问题的目的是为两步数学问题做好铺垫)
2.课件出示例题:一个儿童足球29元,比一个学生笔袋还多8元,84元可以买几个笔袋?
(一)自学提示:
(1)例题与预备题有何异同?
(2)同一个数学问题,哪道题易做,哪道题还不能直接做出来?为什么
(3)解答例题中的数学问题还需要什么条件?
(4) 交流讨论,教师对个别学困生点拨辅导。
(5)学生代表发言,教师补充。
板书:问题一:一个学生笔袋多少元?问题二:需要多少个笔袋?
29-8=21元 84÷21=4(个)
(二)教师精讲小结。
预备题与例题的数学问题一样,但解答的步骤不一样,预备题是一道一步直接计算的数学问题,例题是两步计算的复合数学问题,不能直接计算,要把隐含问题找出来并解答,然后做为解决最后问题其中的一个条件,并与例题中的另一个条件结合起来,最后再解决最后的数学问题。
板书、 一步单一问题 两步复合问题
直接计算 解答隐含问题
(设计意图:从同一个数学问题入手,由一步数学问题铺垫到第二个问题,便于学生理解两者的不同,初步理解两步数学问题的基本结构。)
迁移反馈练习
1.晨光小学有男生300人,女学生312人,每18人组成一个环保小组,能组成多少个小组?
2.红旗小学有学生645人,比晨光小学还多33人,每18人组成一个环保小组,晨光小学能组成多少个环保小组?
3.红旗小学有学生584人,晨光小学比红旗小学还多28人,每18人组成一个环保小组,晨光能组成多少个环保小组?
(1)学习提示:
(这几个数学问题是一步问题还是两步问题?能直接解答吗?)
(要求能组成多少个小组还需要哪一个条件?)
(2)学生自己独立解答,教师巡视指导学困生。
(3)学生代表发言,教师纠正点拨。
(设计意图:出示同样的数学问题,但题目中的隐含问题不同,隐含问题的解决要用到不同的数量关系,便于构建两部数学问题的知识体系,通过一道题的解答,可使学生进行学法的迁移,有利于培养学生的自学能力)
四、课中交流,深化学习
同学们,通过本节课的学习,你能总结两部数学问题的解题思路吗,他们在结构上有何特点?
(设计意图:师生之间,学生与学生之间相互交流,总结两步数学问题的解题思路,与两步数学问题结构特点,对学生学习方法的迁移以及自学能力的培养起到潜移默化的作用)。
五、作业。
1.一箱蜜蜂平均一年可以酿造蜂蜜75千克千克,爷爷养了3箱,爸爸养了9箱,每年总共可以酿造多少蜂蜜?
2.一箱蜜蜂平均一年可以酿造蜂蜜75千克千克,爷爷养了3箱这样的蜜蜂,爸爸养蜂的数量是爷爷数量的3倍,爸爸每年可以收多少千克的蜂蜜?
3.一箱蜜蜂平均一年可以酿造蜂蜜75千克千克,爸爸养了9箱这样的蜂蜜,是爷爷养蜂数量的3倍,爷爷每年可以收多少千克的蜂蜜?
4.一箱蜜蜂平均一年可以酿造蜂蜜75千克千克,爸爸养了17箱这样的蜂蜜,当年卖掉了11箱蜂蜜,余下的蜂蜜有多少千克?
5一箱蜜蜂平均一年可以酿造蜂蜜75千克千克,爷爷养了3箱,比爸爸少5箱,爸爸每年可以收多少千克的蜂蜜?
6.一箱蜜蜂平均一年可以酿造蜂蜜75千克千克,爸爸在养蜂房里搭了一个蜜箱架,共3层,每层放5个蜂箱,爸爸一年可以收多少千克的蜂蜜?
(设计意图:6个数学问题中,每个题中的隐含问题都是11个最基本的数学问题中的一种,也涉及到小学阶段最基础的4类数量关系。这样做,便于学生更加熟练地掌握四种数量关系,而且隐含问题是不同种类的数学问题,要用到加、减、乘、除四种运算方法。这样自然而然就构建起了两步数学问题的知识体系,对于学生学法的迁移,能力的培养都起到积极作用)
板书设计 解决两步数学问题
1.课件出示预备题:1个 笔袋 2.出示例题:一个儿童足球 29元,
21元,84元可以买几个? 比一个学生笔袋还多8元,84元可
以买几个?
一步数学问题 两步数学问题 不
条 1个 笔袋 21元 直 隐含问题: 一个学生笔袋多少元?能
接 29-8=21(元) 直
件 84元 算 问题二: 简介条件 29元 8元 接
直接条件 84元 算
84÷21=4(元) 84 ÷ 21 = 4(个)
84 ÷(29—8)= 4(个)
答:可以买4个笔袋。
(设计意图:板书本节知识的纲要符号,提炼精华内容便于学生掌握知识重点与要点,更加便于学生掌握两步复合数学问题的基本结构与解题思路)。
